Category: Metodică

Motto:  Cu rigla, raportorul şi compasul spre înţelegere, gândire şi învăţare (adaptare după o vorbă nemţească: “mit Kleber und Schere, durch Forschung und Lehre”, pe româneşte: “cu foarfecă şi lipici spre cercetare şi învăţătură”).

În mega-eseul despre planimetrie şi stereometrie, în partea a 3-a, scriam despre un ciudat embargou “pus” asupra planimetriei în clasa a 6-a pentru că de fapt nu am avea ce să calculăm până nu cunoaştem figurile geometrice, în principal triunghiurile, patrulaterele sau cercurile. Am explicat deja că această impresie este una falsă, superficială, şi că de fapt în clasa a 6-a elevii ar trebui să parcurgă o primă fază a planimetriei, constând în lucru efectiv cu instrumentele geometrice pentru măsurări sau construcţii ale unor diferite structuri plane, pentru a conecta înţelegerea fenomenelor de către mintea elevilor cu realitatea despre care se va vorbi ulterior.

Astfel, am explicat că planimetria ar trebui să înceapă prin exerciţii simple de măsurare a unor “obiecte geometrice” deja existente cât şi de construcţii ale unor “obiecte geometrice” cu anumite dimensiuni cerute. Fără această fază iniţială există clar posibilitatea de apariţie la unii elevi a unor elemente de analfabetism funcţional matematic (AFM), chiar şi în acest domeniu deosebit de “aritmetic” al geometriei. Din păcate însă, chiar aşa, cine se mai gândeşte în zilele noastre “să piardă timp” cu astfel de banalităţi?, cum ar fi măsurarea sau cunstrucţia unor elemente de anumite dimensiuni (asta a fost o întrebare retorică). În acest context trebuie să scot în evidenţă gafa metodică uriaşă a multor colegi care susţin la clasă că, dimpotrivă, chiar “figura nu contează” într-o problemă.

Revenind la subiectul de bază, cu alte cuvinte, embargo-ul din clasa a 6-a poate exista doar în mintea celor care privesc geometria numai la nivelul demonstraţiilor şi a calculelor mult prea evoluate, în general a gândirii mult prea înalte pentru o mare parte a elevilor (chiar pentru cea mai mare parte a elevilor!). Trebuie să recunosc că şi eu m-am numărat uneori printre aceştia; şi pentru mine drumul şi paşii de coborâre de la gândirea de profesor experimentat spre nivelul de gândire al copiilor a fost şi este în continuare unul anevoios, şi asta datorită paradigmelor de predare preexistente desigur şi în mintea mea, paradigme pe care deşi le respect, ca dascăl responsabil înţeleg că trebuie să le dau uneori de-o parte pentru a-mi deschide “ochii minţii” şi “a vedea” nevoile reale ale elevilor mei (nu doar nevoile matematicii mele înalte).

În această luptă, eu cu mine însumi, în urma articolului mai sus amintit (mega-eseul despre planimetrie şi stereometrie), dar şi în urma unor ciudate cercetări din timpul primului lockdown (aprilie 2020) în domeniul problemelor de aritmetică, s-a intărit ideea că în clasa a 6-a nu există un embargou asupra planimetriei, ci că la această etapă este vremea unei perioade clare de practică în domeniul măsurărilor şi ale construcţiilor geometrice, începând chiar de la primele elemente. Astfel, eu nu am voie să las însuşirea acestor elemente doar pe seama “învăţării definiţiilor”, ci trebuie să-i ofer elevului începător imediat şi ocazia învăţării acestora în mod practic, această cale susţinând evident şi însuşirea, dar şi fixarea teoretică a noţiunii respective.

După cum am spus deja, demult făceam asta la capitolul de triunghiuri (cu cele două fişe din postarea precedentă), dar acum, în acest început de 2021, mi-am dat seama că trebuie să-mi organizez un material de lucru corespunzător şi pentru primele cunoştinţe de bază ale geometriei: puncte şi drepte, segmente şi semidrepte, colinearitate şi concurenţă, unghiuri, ideea de congruenţă, paralelism şi perpendicularitate, mediatoare şi bisectoare etc. Spun că trebuie să-mi organizez un material de lucru corespunzător şi pentru primele cunoştinţe de bază ale geometriei, pentru că un astfel de material nu există de fapt; în nici o carte, fie ea manual sau auxiloiar, nu am găsit materiale de lucru pentru cunoaşterea elementelor de bază din geometrie prin măsurare şi construcţie, adică având ca obiectiv aceste două acţiuni. În cărţi vechi există probleme de construcţii geometrice, dar acestea sunt mult prea înalte din punct de vedere intelectual.

Noutatea este că acum am reuşit să cobor mult ştacheta gândirii mele, şi mai multca în trecut, spre nivelul minţii copiilor de rând, cât şi spre ideea de cunoaştere a materiei dinaintea triunghiurilor prin munca concretă cu instrumentele geometrice. Astfel, am reuşit să organizez un material cu sarcini absolut elementare, fără a fi plictisitor (sper!), cu sarcini la care trebuie folosite instrumentele geometrice de bază în orice trusă: ideea de riglă negradată pentru simpla trasare a dreptelor (la întâmplare sau cu exactitate prin anumite puncte), dar şi liniarul gradat pentru măsurarea diferitelor lungimi (în mod mai “neortodox” chiar şi liniarul ca instrument de trasare a două drepte paralele, de o parte şi de alta a acestuia); compasul ca instrument pentru trasarea de cercuri, dar şi ca instrument pentru “luarea unei distanţe” între două puncte (inclusiv ideea de congruenţă a unor segmente, mai presus de măsurarea lungimii acestora); raportorul ca instrument de măsurare, dar şi ca instrument de construcţie a unor unghiuri de o anumită măsură; echerul, atât ca instrument de verificare a perpendicularităţii, cât şi ca instrument de construcţie a acesteia, respectiv a unui unghi drept.

Elevii fac astfel cunoştinţă prin intermediul acestor patru instrumente geometrice cu “obiectele geometrice” studiate, măsurându-le sau construindu-le în diferite situaţii, adică lucrând practic cu acestea, nu doar învăţându-le definiţiile şi străduindu-se a le asimila ca noţiuni teoretice.

Problema este că noţiunile se învaţă mult mai bine prin folosirea lor practică (preferabil chiar în mod repetat) decât prin învăţarea unor definiţii teoretice în mod steril (chiar şi în mod repatat). De multe ori se poate observa că un elev care ştie să turuie definiţia, de fapt nu ştie deloc despre ce vorbeşte. Prin materialul din acest eseu încerc să readuc aplicarea acestui principiu natural de învăţare în viaţa elevilor noştri.

Astfel am organizat un set de exerciţii conţinând sarcini simple, cuprinse într-o fişă de lucru destul de generoasă, despre care însă nu am defel pretenţia de a fi perfectă (probabil că după primele folosiri la clasă voi avea tendinţa de a corecta sau completa diferite aspecte din aceasta). Cu alte cuvinte, nu am pretenţia de a vă prezenta un material deosebit de cizelat, dar în cazul de faţă ideea şi intenţia prevalează.

La fel ca în postarea precedentă, şi aici trebuie să fac observaţia asupra faptului că problemele de construcţie sunt poziţionate conform ordinii parcurgerii lecţiilor de către mine (conform principiilor pedagogiei Waldorf). Nu are rost să prezint toată această ordine, dar trebuie să precizez că eu parcurg destul de repede (mai exact în a doua lecţie) o prezentare a poziţiilor relative a două drepte, unde apar deja noţiunile de drepte paralele sau drepte perpendiculare, cu referire la poziţionările orizontale sau verticale şi analogii cu acestea. Cu alte cuvinte, noi învăţăm despre drepte perpendiculare înaintea studiului despre unghiuri; unghiurile apar în a doua jumătate a studiului elementelor de bază. Rog în acest context cititorii să treacă peste acest inconvenient şi să înţeleagă tema principală a prezentării de faţă; oricine poate apoi să-şi redacteze o fişă de lucru conform nevoilor personale.

Acest inconvenient dispare însă dacă fişa este folosită ulterior lecţiilor, ca material recapitulativ. Ca o observaţie personală, trebuie să precizez că această bruscă “iluminare” a mea pe subiectul de faţă are loc prea târziu chiar şi pentru actuala mea clasă a 6-a, astfel încât şi aceştia au primit-o în ultima săptămână a semestrului I ca temă recapitulativă, înaintea orelor despre triunghi. Cred că nu-i rău nici aşa, pe această cale putând merge şi alţi colegi, folosind fişa respectivă ca material suplimentar (după parcurgerea noţiunii de perpendicularitate, după unghiuri, conform ordinii oficiale din programă).

Un aspect colateral important al acestui prim set de exerciţii este şi formarea obişnuinţei elevilor cu textul (mai lung sau mai scurt) conţinând noţiuni geometrice, în general matematice, şi preîntâmpinarea astfel a apariţiei analfabetismului funcţional matematic, în acest domeniu, dar şi în general, deoarece majoritatea cerinţelor sunt la limita de jos a complexităţii. Anexez în final fişa de care am vorbit (patru coli A4). CTG

Fișă

Motto:  Cu rigla, raportorul şi compasul spre înţelegere, gândire şi învăţare (adaptare după o vorbă nemţească: “mit Kleber und Schere, durch Forschung und Lehre”, pe româneşte: “cu foarfecă şi lipici spre cercetare şi învăţătură”).

În mega-eseul despre planimetrie şi stereometrie, în partea a 3-a, scriam despre un ciudat embargou “pus” asupra planimetriei în clasa a 6-a pentru că de fapt nu am avea ce să calculăm până nu cunoaştem figurile geometrice, în principal triunghiurile, patrulaterele sau cercurile. Aşa-i: nu putem să ne ocupăm de perimetre şi de arii până nu cunoaştem serios figurile geometrice “închise”, cărora vrem să le calculăm perimetrele şi ariile (studiul ideii de perimetru sau arie pentru câteva figuri în clasa a 5-a implică o abordare extrem de intuitivă a acestora, abordare care însă este posibilă doar în cazul câtorva, în principal pătratul şi dreptunghiul). Există însă un mare DAR,… , anume că planimetria nu constă doar în calcule de perimetre şi arii.

Ariile reprezintă măsura suprafeţelor (pe germană Flächeninhalt, însemnând “conţinutul suprafeţei”) a unor figuri bidimensionale (2D) şi se calculează conform unor formule (reţete) complexe, ce au făcut obiectul unei “cercetări” preliminare (asta într-un caz normal, în care profesorul doreşte să-i înveţe pe elevi să şi gândească, nu doar să rezolve papagaliceşte nişte exerciţii; dacă însă profesorul sau un părinte îi dă elevului direct formula, atunci elevul va acumula şi cu această ocazie frustrare faţă de incapacitatea sa de gândire, făcând astfel încă un pas spre “analfabetismul funcţional” matematic).

Dimpotrivă, deşi se referă la figuri bidimensionale, perimetrele reprezintă o mărime unidimensională (1D). Procedeul de calcul al perimetrelor este însă unul mult mai simplu, anume de însumare a lungimilor tuturor laturilor. O persoană cu un minim nivel de gândire nu are nevoie de reţetă în cazul unui perimetru (dacă un elev nu reuşeşte să gândească singur un perimetru, dă clare dovezi de “analfabetism funcţional” matematic; un adult care împinge elevul spre învăţarea pe de rost a unor reţete de perimetru la diferitele figuri geometrice, acesta dă dovadă de o inconştienţă crasă, în multe cazuri împingând de fapt elevul şi mai mult înspre mocirla nongândirii, numită “analfabetism funcţional” matematic-AFM; dimpotrivă, dacă un elev îşi deduce singur anumite formule de calcul a perimetrului, aceasta este o clară dovadă de gândire, dar numai dacă o face el, nu şi dacă i-o dă adultul de lângă el; de pildă, un elev care tot adună laturi şi la romb, fără să-şi dea seama că poate înmulţi latura cu 4, acesta are clar un început de AFM, adică de “analfabetism funcţional” matematic).

Încercând să facem un pas şi mai jos faţă de arii şi faţă de perimetre, vedem că înaintea acestora se află simpla preocupare pentru lungimea unor laturi, adică lungimea unor segmente. De aici începe de fapt planimetria, iar clasa a 6-a are din belşug ocazii de a exersa elemente de bază în planimetria iniţială, adică ocazii de lucrat cu măsurile elementelor unor figuri, segmente şi unghiuri.

Cu alte cuvinte, planimetria începe prin exerciţii simple de măsurare a unor “obiecte geometrice” deja existente, cât şi de construcţii ale unor “obiecte geometrice” cu anumite dimensiuni cerute, în principal segmente, adică lungimi, dar apoi repede fiind incluse în acest joc şi unghiurile. Aceste exerciţii existau în toate manualele vechi (ele dispăruseră direct, dar erau subînţelese chiar şi în vremea ultimelor manuale comuniste, cele din anii ’80-’90), dar au fost cu totul abandonate în forma manualelor alternative din 1997, deoarece acestea cât şi preocuparea profesorilor au ajuns să fie setate total spre matematica de performanţă; or, măsuratul cu liniarul şi alte activităţi de acest gen chiar nu fac parte din preocupările concursurilor de excelenţă.

Fără această fază iniţială a geometriei există însă clar posibilitatea ca unii elevi (şi nu puţini) nici măcar să nu priceapă despre ce este vorba în problemele cu arii şi perimetre, acestea prezentându-li-se din start deja mult prea sofisticat şi “teoreticist”. Înainte de a lucra “calculatorist” cu nişte dimensiuni, elevul trebuie să le fi folosit “măsurătorist”, altfel pot apărea disfuncţionalităţi puternice la copiii instabili din acest punct de vedere (AFM).

De pildă, există copii care nu ştiu ce şi cum se măsoară cu liniarul, existând unii care au impulsul să înceapă cu măsurătoarea de la 1, nu de la 0. Nici nu mai are rost în acest context să vorbim despre măsurarea unghiurilor cu raportorul. Acesta este oricum un instrument mult mai complicat decât liniarul, profesorul trebuind să petreacă cu elevii mult mai mult timp la măsurarea unghiurilor, dacât la lungimi. Procentul elevilor care nu pricep din prima ce se întâmplă cu raportorul este muuult mai mare decât în cazul liniarului, iar aceştia au nevoie să lucreze câteva zile pe acest subiect până se fixează şi în mintea lor “ce şi cum”.

Cu alte cuvinte, embargo-ul din clasa a 6-a împotriva planimetriei poate apărea doar în mintea profesorilor care gândesc numai la nivelul demonstraţiilor şi a calculelor sofisticate, în general a gândirii mult prea înalte pentru o mare parte a elevilor.

Ca o paranteză, desigur că cititorul va căuta partea întâi (1) a acestei serii, dar nu o va găsi. Motivul este următorul: am decis să expun acest subiect, al construcţiilor geometrice, în ordinea în care mintea mea l-a cucerit, nu în ordinea în care părţile acestui eseu apar în viaţa elevului. Numerotarea însă se referă la ordinea naturală în predare, iar onor cititorii vor trebui să-şi lămurească această dualitate de abordare (staţi liniştiţi: urmează cât de repede şi partea întâi). Să vedem deci cum am “cucerit” eu acest subiect în ultimul deceniu.

De mulţi ani în mintea mea a început să crească – încetu’ cu-ncetu’ – vechea temă din manuale de demult despre construcţii de triunghiuri cu instrumente geometrice (începând din secolul XIX şi până în anii ’90, când o făceau încă foarte mulţi profesori). În manualele vechi elementele erau desenate separat mai întâi; doar apoi erau desenate asamblat într-un triunghi.

Cu timpul mi-am dat seama că aceasta reprezintă o minunată oportunitate de cunoaştere practică a triunghiurilor, deosebit de bună de aplicat înaintea problemelor cu demonstraţii în triunghiuri; elevii sunt astfel îndrumaţi iniţial spre o cunoaştere practică a acestora, înaintea abordării problemelor “intelectuale”. Pe acest drum de refacere a căii vechi de cunoaştere, de la un an la altu’ fişa mea de lucru a crescut încet-încet; la început a fost scrisă de mână, apoi a ajuns redactată în calculator, evoluând în variante tot mai cizelate şi mai complete. La ora actuală acest material de lucru pentru elevii se prezintă sub forma a două fişe: Fişa 1) Construcţii de triunghiuri (generale sau speciale) şi Fişa 2) Construcţii de triunghiuri cu linii importante. Acestea pot fi imprimate faţă-verso pe o coală A4. Este evident că a doua fişă ajută şi la o primă cunoaştere practică a liniilor importante în triunghi.

Materialul este adaptat formei în care predau eu acest capitol, anume în ordinea următoare: Lecţia 1) Triunghiul (elemente), Suma unghiurilor, unghiul exterior; Lecţia 2) Construcţia triunghiurilor, cazurile de construcţie (renumitele LLL, LUL şi ULU abordate iniţial astfel); Lecţia 3) Clasificarea triunghiurilor (tipuri de triunghiuri); Lecţia 4) Liniile importante în triunghi; Lecţia 5) Triunghiul dreptunghic (tipuri, proprietăţi şi teoreme).

Consider că abia după o cunoaştere practică prin construcţie a triunghiurilor cu instrumentele geometrice, abia apoi se poate trece la nivelul superior, anume la demonstraţii cu acestea. Partea de cunoaştere practică şi intuitivă lipseşte din forma de predare a majorităţii profesorilor, iar acesta este unul din motivele de bază pentru care elevii din toată ţara merg atât de slab la geometrie.

Din păcate, geo-metria (măsurarea terenurilor, cum a fost aceasta denumită de către grecii antici, după vizitele “de studii” în Ţara Nilului) a ajuns în ciudata situaţie de a se dezice de denumirea sa: la ora actuală în geo-metria de mult nu mai măsoară! Prin iniţiativa mea, eu am încercat să repun geo-metria pe făgaşul normal, punându-i pe elevi la început “să măsoare”.

Nu vreau să susţin că geo-metria ar trebui să revină la practicile de măsurare a terenului (de pildă cum se făcea după retragerea apelor Nilului în Egiptul Antic), dar consider că orice elev ar trebui să fie introdus în acest domeniu începând printr-o cunoaştere practică a elementelor geometrice, o cunoaştere care să fie adaptată vârstei şi nivelului mediu de gândire, să fie accesibilă, chiar cu vagi accente ludice, dar în primul rând să fie făcută prin intermediul manualităţii. Această cunoaştere practică nu o exclude pe cea teoretică. Cunoaşterea teoretică trebuie doar domolită şi adaptată nevoilor şi posibilităţilor generale ale vârstei de clasa a 6-a, folosirea ei în probleme de demonstrat trebuind însă să vină întotdeauna după cunoaşterea practică.

În acest context trebuie să recizez că materialul din aceste fişe urcă până la nivelul de dificultate în care rezolvitorul trebuie de fapt, este chiar nevoit, împins să facă primii paşi de raţionamente specifice demonstraţiilor, raţionamente pe care trebuie desigur să le justifice (am făcut aşa pentru că …).

Este evident că după etapa de cunoaştere a triunghiurilor prin construcţie, pe baza “cazurilor de construcţie” (LLL, LUL, ULU, dar şi după o scurtă analiză LUU), se poate trece apoi la probleme teoretice, unde ar trebui parcursă lecţia despre “cazurile de congruenţă” a triunghiurilor (la început a triunghiurilor oarecare, iar apoi şi a triunghiurilor dreptunghice). Este evident că înţelegerea acestor lecţii va fi mult mai solidă, gândirea elevilor având acum formate rădăcini adânci într-o înţelegere practică a fenomenelor. Cu alte cuvinte, este evident că o lecţie ancorată în profunzimea experienţei practice personale are şansa să fie mult mai solidă decât o cunstrucţie superficială, fără o fundaţie solidă.

Anexez în final PDF-uri cu cele două fişe, cu observaţia că materialul conţine inclusiv aplicaţii ale teoremei triunghiului dreptunghic înscris în semicerc (“Cercul lui Thales”, cum este aceasta cunoscută de la graniţa cu Ungaria încolo, adică în toate ţările de cultură germană), teoremă folosibilă în cazul de construcţie IC, cu ipotenuza ca bază a triunghiului. CTG

2A5 Constructii linii imp in tri 35ex-converted.pdf şi
2A5 Constructii Triunghiuri 41ex-converted.pdf

Cred că onor cititorii şi-au dat seama că am redactat acest mega-eseu cu gândul direct la studiul ariilor şi al volumelor corpurilor geometrice din clasa a 8-a, indignat fiind de excluderea acestora din materia de EN în contextul opririi şcolilor în primăvara acestui an bulversant 2020, dar şi speriat fiind de posibilitatea repetării scenariului pentru următoarea generaţie. Dacă în anul şcolar 2019-2020 decizia se mai justifică cumva, pentru anul şcolar 2020-2021 nu mai există nici cea mai mică justificare, datorită faptului că lucrurile puteau fi pregătite din timp (adică din vara anului 2020).

Unul din motivrele plauzibile pentru care nu a fost pregătită, respectiv prevenită repetarea unei astfel de situaţii, este faptul că probabil în Minister atenţia majorităţii este îndreptată cu predilecţie spre vârfuri, spre matematica “de performanţă”; ori, mişcarea de excludere a stereometriei de la EN nu i-a afectat prea mult pe elevii de vârf (cei mai buni dintre ei au primit însă o lovitură “sub centură” prin toamnă, când d-na Ministru filolog a decis să elimine toate olimpiadele din activitatea acestui an, deci inclusiv “sfintele” olimpiade de matematică).

Se pare însă că pe diriguitorii matematicii româneşti nu-i prea interesează ce se întâmplă cu marea masă a celor “slabi la matematică”. Lor le-au dat câteva întrebări tălâmb de banale, astfel încât să nu existe proteste din partea acestora, dar şi pentru ca promovabilitatea pe ţară să fie OK din punct de vedere politic, astfel încât guvernanţii să aibă linişte măcar din acest punct de vedere într-un an electoral agitat cum nu a mai fost altul.

Aşadar, aceasta a fost motivaţia mea principală, pentru redactarea ideilor exprimate, cea din punct de vedere a afectării stereometriei. În cadrul acestui mega-eseu am folosit însă ocazia pentru a atinge şi alte aspecte colaterale, care însă sunt înrudite ca fenomenologie, respectiv ca atitudine a organizatorilor din Minister, a autorilor de manuale sau a marii majorităţi a profesorilor, care însă toate afectează la diferite vârste învăţarea matematicii şi formarea gândirii la marea masă a elevilor.

Unul din “punctele” respective îl reprezintă planimetria, mai ales studiul ariilor în clasa a 7-a, despre care am vorbit în diferite rânduri. În contextul studiului ariilor există multe aspecte implicate. Haideţi să analizăm mai atent două dintre acestea şi felul în care ele interacţionează. Precizez că este vorba de aspecte ale predării noastre ca profesori în România acestor ani, aspecte care însă nu sunt defel şi niciunde discutate: nici în materialul însoţitor al programei noi din 2017, nici în cursurile de formare, nici în manuale, niciunde!

Un prim aspect la care mă gândesc este faptul că planimetria capătă un sens evoluat, un sens cu adevărat matematic, doar odată cu posibilitatea calculului unor lungimi prin teorema lui Pitagora. Fără teorema lui Pitagora calculul ariilor şi a perimetrelor se rezumă la aplicarea unor reţete, adică a unor formule anterior dobândite (deduse prin gândire sau primite “de-a moaca”), şi a finalizării corecte a calculului din acestea (care se rezumă de obicei la aritmetică de clasa a 5-a, eventual la calcule cu proaspăt învăţatele numere iraţionale). De-abia prin teorema lui Pitagora calculul de arii şi perimetre devine MATEMATICĂ, devenind adică o situaţia de gândire, de forţare a individului în a decide singur ce paşi trebuie să facă, de a alege şi a combina diferite procedee anterior învăţate într-un întreg, care să parcurgă în mod coerent drumul de la ce se dă la ce se cere. De abia prin posibilitatea folosirii teoremei lui Pitagora planimetria urcă de la nivelul unui calcul banal la nivelul superior al problemelor de matematică. Cu alte cuvinte, folosirea teoremei lui Pitagora îl obligă pe elev să urce de la aplicarea “contabilicească” a unei formule, a unei reţete, la un nivel elevat în care el, elevul, trebuie să gândească, adică să ia decizii despre ce procedeu să aplice în fiecare moment.

De abia prin integrarea teoremei lui Pitagora în probleme planimetria urcă la un nivel de complexitate comparabil cu cealaltă mare parte a geometriei, anume cu demonstraţia geometrică. Totuşi, chiar dacă urcă de la nivelul de “exerciţii” (aplicarea şi exersarea unei simple reţete individuale) la nivelul de “problemă” (combinarea mai multor reţete individuale într-un întreg mai complex, combinare ce are loc, cum spuneam, în urma unor decizii ale rezolvitorului, ce reprezintă deja un proces de gândire), planimetria rămâne oricum la un nivel mai accesibil majorităţii elevilor pentru că răspunde la mult mai obişnuita întrebare “CÂT?”, pe când necesitatea demonstraţiei apare în urma întrebării “DE CE?”. Or, întrebarea “CÂT?” este mult mai prezentă în cotidianul majorităţii oamenilor, inclusiv a celor mai mulţi elevi, fiind ca atare mult mai accesibilă majorităţii indivizilor, decât întrebarea “DE CE?”, care este evident o întrebare mai profundă (vedeţi, asta numesc eu o adevărată psiho-pedagogie; şi când mă gândesc câţi ani m-am uitat cu dispreţ la cartea prof. Eugen Rusu despre Psihologia activităţii matematice).

Cu întrebarea “CÂT?” elevul se confruntă din clasele primare, aceasta reprezentând deci parte a zonei sale de confort intelectual matematic, chiar şi măcar datorită faptului că s-a confruntat cu astfel de situaţii de multe ori. Această întrebare este specifică gândirii infantile, anume a stadiului operaţional concret, aşa cum îl denumea Piaget, deşi problemele de calcul a ariilor şi a perimetrelor încep să folosească elemente ale gândirii adulte, din stadiul operaţional formal. Dimpotrivă, problemele de demonstraţie, cele care răspund la întrebarea “DE CE?”, lucrează predominant la nivelul gândirii adulte, adică în stadiul operaţional formal al raţionamentelor.

Vreau să spun aici că problemele de planimetrie reprezintă o cale de formare şi de exersare a gândirii mult mai accesibilă marii majorităţi a elevilor decât problemele de demonstraţie. Mai mult, toate problemele de demonstrat (inclusiv cele de calcul, dar care folosesc artificii algebrice sau de demonstraţie geometrică) reprezintă perioade ale orei de adresare şi educare exclusivă a elitelor, a elevilor de vârf (de obicei 2-3 în clasă). Dimpotrivă, problemele de calcul reprezintă perioade de adresare generală a întregii clase, adică şi a marii majorităţi a elevilor, din care însă înţeleg şi cei buni (şi, să ştiţi că nu li se usucă creierul de puţină “artimetică”).

Mai mult, în aceste perioade, elevii de vârf au ocazia să exerseze EMPATIA, dar şi o stare de respect plină de îngăduinţă faţă cei care le sunt inferiori din punct de vedere al gândirii. Dimpotrivă, toate acele perioade ale orei când se lucrează doar pentru vârfurile clasei, îi educă pe aceştia înspre o stare îngâmfată egoist-egocentristă, ce nu are nimic în comun cu educarea respectului mutual ce ar trebui să existe între membrii unei societăţi civilizate.

Cu alte cuvinte, prin problemele de planimetrie şi stereometrie profesorul de matematică are o ocazie mult mai accesibilă de a deveni un formator de gândire, decât prin intermediul demonstraţiilor geometrice. Marea majoritate a elevilor, cei cca. 70-80% care formează corpul de bază al “clopotului lui Gauss”, vor putea face pasul spre gândire prin intermediul problemelor de calcul de perimetre, arii sau volume, pe când în cazul problemelor de demonstrat aceştia vor fi tentaţi să înveţe pe de rost, mimând că gândesc, gândirea adevărată rămânând “de căruţă” (vezi şi P.S. din final, cu alte aspecte legate de acest important gând).

Până la programa din 2017 acest pas (introducerea teorema lui Pitagora în calculul ariilor) nu era posibil în cadrul capitolului din toamna clasei a 7-a, evident pentru că elevii încă nu aveau parcursă teorema lui Pitagora, aceasta fiind poziţionată în programă de abia în semestrul al II-lea, fixată fiind acolo de acceptarea doar a demonstraţei prin teorema catetei, care la rândul ei trebuia în prealabil demonstrată prin asemănarea triunghiurilor. Ca o paranteză fie spus, atenţionez că există şi demonstraţii prin arii la teorema lui Pitagora (încă multe chiar), demonstraţii ce ar permite includerea acestei teoreme în capitolul de arii (eu am ales una dintre ele, incluzând-o astfel de 20 de ani în studiul ariilor din toamna clasei a 7-a), dar acesta este un alt subiect şi nu vreau să intru în el acum.

Dimpotrivă, după programa din 2017, programă ce implică predarea “în gol”, adică fără demonstraţie, a teoremei lui Pitagora în finalul clasei a 6-a, n-ar mai trebui să ne împiedice nimic în integrarea acestei teoreme în studiul ariilor din toamna clasei a 7-a. Orice demonstraţie la teorema lui Pitagora implică parcurgerea unor elemente dificile, din categoria demonstraţiilor, înainte de aplicarea banală a calculului în probleme de planimetrie (absolut ciudat, dar acest fenomen nu apare şi în stereometrie, unde se poate intra în mod intuitiv direct în calcule, fără a fi nevoie de demonstraţii prealabile). Dimpotrivă, situaţia ciudată creată de programa din 2017 ne scuteşte de acest aspect al rigurozităţii, dând “mână liberă” profesorului de a folosi din start teorema lui Pitagora la calculul de arii şi perimetre. Şi totuşi, în aceste condiţii “ideale” pentru profesor de a face un pas clar în favoarea majorităţii elevilor, cei mai mulţi profesori se fac că nu văd, ratând această oportunitate, unii chiar luptându-se împotriva acesteia.

În acest sens, poate fiecare să studieze cum arată situaţia în manualele sau în culegerile auxiliare însoţitoare alese; unii le-au integrat timid, alţii dimpotrivă nu s-au gândit la această posibilitate (eu personal nu am făcut un astfel de studiu cât de cât vast; vorbesc doar în urma întâlnirii unor câteva exemple din ambele categorii). Care este însă situaţia de la clasă în acest context? Păi, cam aceeaşi: profesorii nu se bagă, nu văd oportunitatea, le este “nu ştiu cum” să iasă din zona de confort a predării din ultimii zece ani.

În acest sens vreau să prezint un singur exemplu: chiar zilele acestea, după publicarea părţii (4) a acestui mega-eseu, m-am întâlnit din nou cu o situaţie absurdă şi am promis că o voi prezenta. Este vorba despre situaţia unei probleme din capitolul de arii din clasa a 7-a, în care, la propunerea unui elev de a rezolva cu teorema lui Pitagora, profesorul spune ad-literam: încercăm să evităm folosirea lui Pitagora (aproape că ai impresia că-l vezi pe acel profesor “scrâşnind printre dinţi” o înjurătură la adresa cui o fi decis introducerea acelei lecţii în finalul clasei a 6-a). Este NOAPTEA MINŢII să lucrezi întreg acest capitol fără teorema lui Pitagora, deşi de data asta elevii o cunosc, doar aşa, pentru că tu te-ai obişnuit să predai acele lecţii fără Pitagora şi îţi este greu să te schimbi. Analizând situaţia concret am putut vedea gândul mai profund al respectivului profesor, anume că el pregătise problema pentru o anumită rezolvare, care era mai scurtă, dar mai “algebrică” decât cea prin folosirea teoremei lui Pitagora (aceasta fiind însă din punct de vedere al elevilor mai accesibilă pentru că era mai “aritmetică”, chiar şi prin prisma celui mai bun elev din clasă, cel care venise cu propunerea). Da, “stimaţi” colegi, dar într-o astfel de situaţie suntem obligaţi să explicăm situaţia elevilor, nu doar să le refuzăm soluţia în mod schizofrenic, pentru că altfel lucrurile rămân în mentalul întregii clase la un nivel inerxplicabil mustind de subiectivitate: de ce să evităm folosirea lui Pitagora de vreme ce o cunoaştem? Vedeţi cum situaţia capătă aspecte conflictuale prin impulsul unei astfel de contra-întrebări retorice.

Cum s-ar fi putut evita astfel de situaţii? Păi simplu, dacă în textele însoţitoare ale programei din 2017 ar fi fost prevăzute şi incluse aceste aspecte, dacă ar fi fost clar precizate, atunci autorii de manuale le-ar fi integrat clar şi vizibil, iar profesorii s-ar fi adaptat evident. Aşa, după cum am mai spus, fiecare ocazie de reformă adevărată şi profundă este ratată în România cu mare stil şi eleganţă balcanică, astfel încât cei de la baza învăţământului, profesorii de rând şi orele lor în nici un caz nu au cum să evolueze în favoarea marii majorităţi a populaţiei şcolare.

Am precizat, mai ales la geometria în spaţiu din clasa a 8-a, că avem de fapt o formă de predare orientată după criteriile rigurozităţii matematicii, dar care sfidează criteriile pedagogice (înţelegeţi ce am vrut cu axele acelea ciudate din prima parte a eseului). Această formă este accesibilă vârfurilor populaţiei şcolare, dar se desfăşoară mult prea sus din punct de vedere intelectual pentru cea mai mare parte a elevilor. Probabil că mulţi dintre matematicieni nu înţeleg de ce “prostimea” nu face faţă geometriei, pentru că doar, măcar ariile şi volumele din clasa a 8-a “sunt simple”. Acelaşi fenomen se întâmplă însă şi cu un an înainte, în clasa a 7-a la studiul ariilor, din cauza a două aspecte, unul dintre ele fiind cel discutat mai sus.

Un al doilea aspect de analizat ar fi următorul: studiul ariilor are două părţi destul de bine delimitate, cu adresabilitate destul de diferită la nivelul elevilor. Pe de o parte avem calculul concret ar ariilor, ce se face cu diferite formule (majoritatea figurilor au mai multe formule, în funcţie de situaţia datelor, şî acestea cu adresabilitate diferită la nivelul elevilor, dar nu mai pornesc şi în acest sens o analiză specială). Pe de altă parte, avem studiul proprietăţilor ariilor, cu figuri echivalente (de obicei necongruente, dar cu aceeaşi arie), rapoarte de arii sau diferite relaţii între elementele unor figuri, relaţii demonstrabile cu ajutorul ariilor. De obicei, în această parte nu se cere calculul unei arii. Prin excelenţă, apogeul acestui domeniu matematic îl reprezintă chiar teorema lui Pitagora, anume că aria pătratului construit pe ipotenuză este egală cu suma ariilor pătratelor construite pe catete (deşi în mentalul multor profesori din România pare că este prohibită).

Din a doua parte, cea mai accesibilă şi cunoscută este proprietatea de arie a medianei, anume că mediana împarte triunghiul în două triunghiuleţe cu ariile egale, deşi de obicei acestea nu sunt congruente. Şi lungimea înălţimii pe ipotenuza unui triunghi dreptunghic poate fi demonstrată aici foarte uşor, prin egalarea a două formule de arie a acestuia. Anexez aici două din problemele mele preferate în această parte de geometrie.

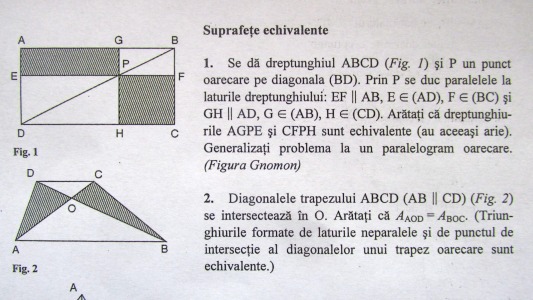
Eu am scos în evidenţă existenţa celor două părţi destul de diferite încă din 2005, la redactarea culegerii de geometrie publicată în 2006 împreună cu soţia mea (De la Cercul lui Thales la Moneda lui Ţiţeica, Probleme elementare de geometrie plană, Ed. Humanitas Educaţional). În această lucrare am cuprins două capitole separate cu arii: Cap. V – Calcule de arii şi perimetre, respectiv Cap. VI – Proprietăţile ariei (problemele de mai sus sunt primele două din acest capitol). Cap. V este adresat, cel puţin în prima sa parte, elevilor de rând, cuprinzând multe probleme de calcul elementar de arii şi perimetre ale figurilor de bază, pe când Cap.VI se adresează prin excelenţă doar elevilor buni la matematică.

Problemele de felul celor două (mai sus prezentate) sunt destul de şocante pentru cei mai mulţi elevi, pur şi simplu pentru faptul că sunt probleme de arii, dar în care elevul nu primeşte nici un număr cu care să calculeze. Arii, dar fără numere, cum vine asta??? Chiar şi cel mai bun elev este bulversat de această situaţie. Diferenţa dintre elevii de vârf şi cei de rând este că cei buni reuşesc să-şi revină din această bulversare, pe când cei de rând nu. Există desigur şi probleme “parşive” în acest sens, probleme în care rezolvitorul primeşte numere (de obicei un număr), dar problema nu este una tradiţională “de calculat”, ci una de comparare de arii. Iată un exemplu la repezeală în acest sens: Considerăm un triunghi oarecare ABC de arie 234 cm² şi notăm cu M, N şi P mijloacele laturilor sale. Demonstraţi că patrulaterul AMNP este un paralelogram şi determinaţi aria acestuia. Problema are un număr, dar nu ai ce să calculezi mare lucru cu acesta. Putem explica şi astfel: la acel paralelogram, nu-i poţi calcula nici o latură, nici o înălţime (aşa cum art cere formula de bază).

Rezumând, putem spune că neconştientizarea existenţei acestei delimitări destul de clare între cele două domenii, alături de neimplicarea teoremei lui Pitagora în capitolul de arii din semestri I al clasei a 7-a, contribuie împreună la ratarea momentului acestui capitol înspre atragerea elevilor de rând către fenomenul matematic. Mulţi profesori bombardează clasele cu probleme din partea de proprietăţi a ariilor, accesibile doar vârfurilor, astfel încât toţi elevii de rând din aceste clase ratează oportunitatea conectării cu gândirea, chinuindu-se în cel mai bun caz să înveţe pe de rost rezolvările respectivelor probleme. Aceasta, împreună cu faptul că elevii nu primesc dreptul de a folosi teorema lui Pitagora în calcule, îi menţine pe cei mai mulţi într-o stare de profundă prostie matematică, tăindu-le posibilitatea accesării gândirii prin fereastra de oportunitate numită “arii”.

Avem şi aici un bun exemplu prin care profesorimea împinge elevii spre analfabetism funcţional matematic, aspect ce iese apoi la iveală în mod dureros la examenul de EN sau la studiile PISA, dar şi cu alte ocazii. Degeaba avem câteva vârfuri cu care ne tot mândrim, când în paralel avem o politică aparent gândită doar spre îndobitocirea maselor.

Dar nici măcar această parte despre proprietăţile ariilor nu este predată corect. De multe ori elevii primesc probleme din această parte, fără să aibă predate înainte elementele necesare (profesorul de mai sus s-a trezit după o săptămână că nu le-a dat proprietatea de arie a medianei, necesară într-o problemă de la temă). Eu văd însă un aspect negativ mult mai profund. Această parte de proprietăţi a ariilor se împarte şi ea în două subpărţi. Există aici foarte multe aplicaţii care sunt exprimabile uşor în limbaj algebric, spre care tind cei mai mulţi profesori, dar există aici şi aplicaţii cu un profund caracter vizual grafic. Cele cu caracter algebric sunt mai statice (de pildă faptul că produsul dintre o latură a unui triunghi şi înălţimnea corespunzătoare este acelaşi, indiferent de latura aleasă ca bază), pe când cele cu caracter mai vizual grafic sunt oarecum “în mişcare” (de pildă faptul că aria unui triunghi nu se modifică dacă “plimbăm” un vârf al acestuia paralel cu latura opusă). Această a doua parte, care dezvoltă o mobilitate mai bună în gândire, este cu totul neglijată în România, fiind abandonată total după reforma din 1997.

*

Încerc să mă opresc aici, deşi este evident pentru orice cititor că aş putea continua cu alte şi alte aspecte “mult şi bine”. Sunt sigur că acest mega-eseu are clar un aer destul de haotic, trecând uneori neaşteptat “de la una la alta”. Este evident că la o a doua reluare lucrurile ar fi mult mai ordonate, dar acest eseu a fost publicat în “timp real”. Iniţial am gândit 4, ba nu 5 părţi (una introductivă şi câte una pentru fiecare clasă gimnazială), iar apoi am spus că mai adaug şi una de concluzii, deci 6, pentru ca în final să ajung la 8 părţi.

Nutresc însă speranţa, că cititorul de bună credinţă a putut căpăta o idee solidă despre cum ar trebui integrate elementele de planimetrie şi de stereometrie în materia de gimnaziu, într-un mod cât mai just relativ la cele trei axe de referinţă prezentate iniţial: 1) axa calcule – demonstraţii; 2) axa 2D – 3D; 3) axa pedagogie – ştiinţă. Nutresc speranţa că am reuşit să atrag atenţia cititorilor asupra acestei problematici importante şi că aceştia şi-au făcut o idee cât mai sănătoasă despre “traseul” pe care noi profesorii ar trebui să-i conducem pe elevi prin “meandrele octantelor” apărute între aceste trei axe de referinţă ale predării geometriei gimnaziale (octantele reprezintă “optimile” în care este împărţit spaţiul de către trei axe de coordonate; octantele sunt similarele cadranelor în sistemul de două axe; cadranele reprezintă “colţuri 2D”, pe când octantele “colţuri 3D”; m-am referit aici la imaginea cu cele trei axe din prima parte a eseului).

Mai sunt doar câteva aspecte pe care nu le-am putut integra fluent în începutul acestui episod, aşa încât le-am păstrat pentru final, în următorul Post Scriptum. Sper să mă pot limita la 8 părţi pentru acest mega-eseu (8 este un număr foarte favorabil din punct de vedere Feng Shui), dar nu pot “băga mâna-n foc” că nu mă va mai apuca din nou scrisul pe acest subiect. Constantin Titus Grigorovici

P.S. Spuneam mai sus că prin problemele de planimetrie şi stereometrie profesorul de matematică are o ocazie mult mai accesibilă de a deveni un formator de gândire pentru marea masă a elevilor, decât prin intermediul demonstraţiilor geometrice. Marea majoritate a elevilor, cei cca. 70-80% care formează corpul de bază al “clopotului lui Gauss”, vor putea face pasul spre gândire mult mai lesne prin intermediul problemelor de calcul de perimetre, arii sau volume, pe când în cazul problemelor de demonstrat aceştia vor fi tentaţi să înveţe pe de rost, gândirea adevărată rămânând “de căruţă”.

Acest aspect este susţinut şi de faptul că în calculul de arii şi perimetre elevul are de combinat calculele teoremei lui Pitagora cu formulele de arie specifice figurii respective, adică are de ales dintre decizia de aplicare între puţini “paşi logici” (la care se adaugă situaţiile banale din cazul perimetrelor), pe când în cazul demonstraţiilor elevul are de ales dintre mult mai mulţi paşi logici posibili (deja învăţaţi), pentru combinarea într-o demonstraţie corectă. Cu alte cuvinte, combinarea unei rezolvări de planimetrie este mult mai simplă decât majoritatea situaţiilor de combinare a unei probleme de demonstraţie.

Ca o scurtă paranteză, precizez că în nici un caz nu ar trebui să le dăm elevilor de învăţat “formule pentru perimetre”. Fenomenul perimetrelor este atât de simplu, încât profesorul ar trebui să le pună din start la baza ideii de gândire. Acolo unde profesorul observă că elevul are tendinţa să înveţe pe de rost “o formulă de perimetru”, acolo trebuie intervenit de urgenţă pentru a atrage mintea elevului înapoi pe linia de gândire. Una este ca elevul să fi dedus singur şi să ştie că perimetrul unui romb este 4a (de 4 ori latura) şi să o poată explica de unde vine,  iar alta este să vedem că elevul nu ştie de unde vine această “formulă”, dar a învăţat-o pe de rost, eventual şi-a şi notat-o într-o listă după care o repetă şi este ascultat acasă, de către un părinte binevoitor, dacă “o ştie”.

Merită făcută aici şi o altă scurtă observaţie metodică, în vederea oportunităţii de formare a gândirii, în sensul de antrenare a minţii elevului în a lua deciziile juste în fiecare caz în parte (vorbesc aici de situaţii din planimetrie, unde, cum am spus, procesul decizional este la un nivel mult mai accesibil). În general există două tipuri de rezolvări prin teorema lui Pitagora. Există pe de o parte cei care scriu relaţia întotdeauna în formă de sumă, urmând ca în cazul când necunoscuta este o catetă, aceasta să fie calculată în final prin procedee specifice ecuaţiilor (trecut în membrul celălalt cu semnul schimbat. Această rezolvare se bazează pe faptul că elevul ştie foarte bine să rezolve ecuaţii, dar în cazul unui elev care a cam ocolit învăţatul în ultimii ani, sau nu poate face lesne transferul de cunoştinţe dintr-un capitol în celălalt, învăţarea problemelor cu teorema lui Pitagora este subminată.

Dimpotrivă, există şi cei care aplică teorema lui Pitagora în două forme, de sumă, dacă ştim ambele catete şi avem de calculat ipotenuza, respectiv de diferenţă, dacă nu cunoaştem o catetă, pornind de fiecare dată cu latura necunoscută. Aparent, aici elevul are de învăţat două rezolvări în paralel (în loc de una) şi mai are de luat şi o decizie în plus, anume pe care dintre cele două să o folosească în fiecare caz. În această rezolvare, însă, elevul nu este dependent de abilităţile dintr-un capitol precedent de algebră, ci rezolvarea se resrânge doar la aplicaţii aritmetice. Apoi, această a doua rezolvare îl antrenează pe elev de a lua decizii încă într-un loc. Pe lângă faptul că-l învăţăm pe elev să aplice anumite reţete, anumiţi algoritmi, ca profesori, noi trebuie să-l învăţăm să şi gândească, măcar câtuşi de puţin şi pe elevul cel mai slab la matematică. Mie personal, această a doua variantă de rezolvare prin Pitagora îmi oferă o astfel de ocazie de formare a gândirii şi la cei mai “începători” la matematică.

Merită să adaug aici încă un aspect ciudat legat de învăţarea matematicii. În general, lumea trăieşte cu impresia că învăţatul matematicii este ca un tren al cărui traseu trebuie să îl parcurgi neapărat pornind de la prima staţie, pe rând prin toate celelalte. Eu sunt însă de altă părere, anume că pe lungul traseu al acestui tren există anumite staţii în care un elev se poate urca cu succes, fără însă să fi parcurs în prealabil toate celelalte dinainte. De ce nu le-ar fi parcurs? Păi, din lene, sau poate datorită unei predări mult prea elevate din partea profesorului, căreia elevul pur şi simplu nu i-a făcut faţă, sau din cine ştie ce alte motive.

Pentru astfel de elevi (care nu sunt deloc puţini), calculul de arii şi perimetre din clasa a 7-a, cu aplicarea teoremei lui Pitagora, reprezintă o astfel de oportunitate rară de a se urca în “trenul gândirii matematice” cu multă eficienţă şi succes, crescând puternic moralul şi dispoziţia unui astfel de elev în a învăţa matematica (creierul său crează cu această ocazie sinapse de gândire şi învaţă să le folosească, urmând ca aceste conexiuni să fie utilizate ulterior şi în alte situaţii). Apoi, odată pornită gândirea matematică, un astfel de elev reuşeşte cu timpul să recupereze şi multe alte elemente dintre cele pierdute înainte. Uneori o astfel de recuperare poate fi absolut spectaculoasă, ridicând elevul de la nivelul unui analfabetism funcţional matematic extrem (la începutul clasei a 7-a) până la nivelul de intrare la liceu într-o clasă de ştiinţe.

Am văzut în acest eseu-serial cum la geometria în spaţiu din clasa a 8-a avem de fapt o formă de predare orientată după criteriile rigurozităţii matematicii, dar care sfidează criteriile pedagogice. Această formă poate fi înţeleasă de către vârfurile populaţiei şcolare, dar se desfăşoară mult prea sus din punct de vedere intelectual pentru cea mai mare parte a populaţiei şcolare. Probabil că mulţi dintre matematicieni nu înţeleg de ce “prostimea” nu face faţă geometriei, pentru că doar, măcar ariile şi volumele “sunt simple”. Păi, DAAAA!, chiar şi lucrurile simple devin de neînţeles pentru mulţi dacă sunt prezentate în context complicat sau într-o formă fără sens! Iar după o vreme apare atât negarea şi refuzul, din punct de vedere psihologic, cât şi incapacitatea pură de a urmări şî a înţelege un conţinut, chiar dacă acesta este prezentat evident simplu, din punct de vedere al capacităţii intelectuale. Cu alte cuvinte, o predare mult prea elevată duce la îndobitocirea maselor!

Haideţi să vă prezint ce amintiri am eu despre clasa a 8-a în legătură cu acest subiect, al studiului poziţiei relative a dreptelor şi planelor şi a demonstraţiilor cu acestea înaintea elementelor de stereometrie. Nu ţin minte mai nimic, în afara faptului că după o anumită oră din clasa a 8-a m-am dus acasă şi mi-am construit o mică machetă pentru teorema celor trei perpendiculare (o machetă foarte mică, la care “planul” era reprezentat de un dreptunghi de la o cutie de chibrituri, care la vremea respectivă încă erau făcutedin plăcuţe foarte subţiri de lemn lipite împreună cu hârtie). Singura datare clară a momentului respectiv este că a fost cândva înainte de Crăciun, pentru că respectiva machetă a ajuns atârnată în bradul împodobit, şi a rămas mulţi ani printre podoabele pentru pom (chiar şi când eram prin facultate o mai găseam acasă la părinţii mei în bradul de Crăciun).

Nu am amintiri de geometrie în spaţiu dinaintea acestui moment, dar bănuiesc ca ceva am înţeles din acele ore, de vreme ce am priceput teorema respectivă, despre care ţin minte o stare de relativ entuziasm, după care am putut să fac corect macheta respectivă când am ajuns acasă. Precizez că am făcut-o din proprie iniţiativă; nu a fost temă. Următoarele amintiri le am despre formulele de arii şi volume, undeva prin primăvară.

Cu alte cuvinte, şi atunci, pe forma de manuale ale lui Hollinger, în ultimul an de valabilitate al acestora (1980-1981), toamna era ocupată de studiul relativ detaliat al dreptelor şi planelor, un studiu greu şi pentru elevii cu o vedere geometrică bună (nu am nici cea mai mică amintire despre probleme sau teste, dar probabil că nici nu făceam mare lucru; problemele adevărate în acest sens au venit la a doua trecere, în clasa a 10-a). Cât era acest studiu de detaliat, dar totuşi prezentat pe baze intuitive, se poate vedea din oricare manual din anii ’60-’70. Nu mi-am propus acum să vă prezint această formă într-un studiu detaliat (cea din timpul şcolii mele), dar este evident că respectivele manuale ar trebui studiate şi actualmente, atât de către autorii de programe, cât şi mai ales de către autorii de manuale.

Mai am însă o relatare despre acest subiect, una profund diferită şi totuşi pe aceeaşi linie, anume de la mama mea. Zilele acestea (după publicarea primelor patru părţi ale prezentului eseu) îi povesteam mamei mele despre acest subiect şi iată ce mi-a povestit (la telefon). Partea de studiu a dreptelor şi planelor i-a fost una dintre cele mai urâte părţi din matematică, vorbind aici cu referire la clasa a 10-a (Mama a predat toată cariera ei în liceu). De abia după ce apăreau corpurile şi apăreau cerinţe pe corpuri, de abia atunci simţea că elevii încep să înţeleagă respectivele situaţii (nu vorbea aici de arii şi volume, ci doar de studiul comportamental al dreptelor şi planelor în spaţiu). Cu alte cuvinte, nici măcar în clasa a 10-a, la o a doua trecere prin subiect) elevilor nu le erau accesibile problemele cu demonstraţii în spaţiu dar fără corpuri (vorbim aici de liceul din Or. Victoria, ca un eşantion destul de reprezentativ pentru toată ţara: cu reprezentanţi ai elevilor din toate nivelele, de la cei ce urmai să ajungă muncitori de rând, apoi mulţii viitori intelectuali, până la cei ce urmau să ajungă în cele mai înalte poziţii universitare, la nivel naţional sau internaţional, şi până la locul I la Olimpiadele naţionale de matematică).

Traduc eu: problemele pe structuri artificiale, de tipul celei date azi vară la EN-8, sunt mult mai greu de înţeles pentru elevi decât situaţiile prezentate în corpuri, care sunt nişte structuri mai uşor de înţeles. Corpurile acţionează aici ca un fel de “schelă” suport pentru înţelegerea şi gândirea elevului, pentru capacitatea sa de imaginaţie în spaţiu; desigur că în lipsa acestei schele elevul se descurcă mult mai greu. Acest aspect a fost recunoscut pe la sfârşitul anilor 2000, când s-a decis introducerea rapidă a corpurilor la începutul clasei a 8-a, într-o formă descriptiv intuitivă, astfel încât să se poată parcurge din start în mod echilibrat şi probleme “în corpuri”, nu doar pe structuri artificiale. Din păcate “onor ministerul” nu a explicat niciodată aceste aspecte, lăsând totul la bunil simţ al profesorilor.

Ordinea naturală ar fi dimpotrivă următoarea: De la început probleme cu drepte şi plane doar pe corpurile deja studiate, iar doar de la un anumit moment probleme pe structuri artificiale. Eu, de pildă, studiez mai întâi toate prismele şi piramidele; apoi studiez lecţiile uşoare despre drepte şi plane doar pe corpuri (unghiul dintre două drepte necoplanare, drepte necoplanare perpendiculare, dreaptă perpendiculară pe plan, plane perpendiculare, drepte paralele, dreaptă paralelă cu un plan, cât şi planele paralele). La acestea elevii primesc o structură artificială teoretică urmată imediat de aplicaţii pe corpuri, transferul fiind ajutat de către folosirea cretelor colorate (întotdeauna aceleaşi culori şi pe structura teoretică şi în mod corespunzător pe corpul geometric din problemă). Structurile artificiale le introduc abia la teorema celor trei perpendiculare. Din acest moment apar apoi şi aplicaţii ale celorlalte în structuri artificiale.

Pentru cei care au uitat problema de azi vară şi nu înţeleg la ce mă refer când vorbesc de probleme pe structuri artificiale, o reiau pe scurt: În Figura 3 este reprezentat un dreptunghi ABCD cu AB = 24 cm şi BC = 10 cm. Punctul O este intersecţia dreptelor AC şi BD, iar dreapta EO este perpendiculară pe planul (ABC). Punctele M, N şi P sunt mijloacele segmentelor AB, AD, respectiv AE etc.

Mama vorbea de elevii de a 10-a, la o a doua parcurgere; la cei de a 8-a, la primul contact cu situaţia respectivă, fenomenul este desigur şi mai dur. Atât de dur încât mulţi dintre elevii care poate ar învăţa geometria în spaţiu, după un astfel de prim contact se sperie atât de tare, încât cu greu mai pot fi recuperaţi. Iar după reforma din 1997, când s-a scos geometria sintetică din liceu, elevii nu mai au oricum o a doua şansă de a înţelege acest studiu.

Apare aici o situaţie de ordin filozofic: dacă studiul dreptelor şi planelor este atât de important din punct de vedere al matematicii, atunci de ce nu este reluat în liceu? Dimpotrivă, dacă acest studiu nu este totuşi atât de important, atunci de ce se insistă cu introducerea acestuia înainte de elementele de stereometrie, care sunt evident mult mai accesibile marii majorităţi a elevilor? Păi, sunt sau nu importante?

Revenind la amintirile mele, trebuie să precizez accentuat că efectiv nu am amintiri din clasa a 8-a înaintea teoremei celor trei perpendiculare. Din clasa a 10-a, când am reluat această materie, nu am astfel de “lipsusuri”, dar trebuie înţeles că eu am avut dintotdeauna o foarte bună vedere geometrică. Dimpotrivă, mulţi elevi nu au nativ o vedere geometrică bună. La aceştia profesorul trebuie să aibă mult tact pedagogic pentru a-i ajuta să-şi formeze minime capacităţi în acest sens (voi reveni cu o altă ocazie asupra acestui subiect).

Rezumând cele două amintiri, ale mele din clasa a 8-a, cât şi ale mamei mele de profesoară în liceu, putem spune că elevul obişnuit trăia o stare bulversantă în care reacţia naturală era cea de “ghiocel”: să stai cuminte, cu capul aplecat şi să speri că “azi nu o să te pună pe tine”. La aceste lecţii elevul de rând trăieşte o frică profundă, refugiindu-se în copierea lecţiei cuminte, iar apoi acasă, în copierea temei de la cineva care o ştie sau de la un coleg care o are (de la altcineva care o ştie) aceasta este o situaţie specifică sistemelor autoritare. Creştinismul Evului mediu a inventat-o prin vânătoarea de vrăjitoare, dar şi comunismul a practicat-o intens: să te simţi vinovat că nu îndeplineşti cerinţele cerute (renumitul plan de producţie), ca să stai “ghiocel” şi să nu emiţi pretenţii. Din păcate, această stare se păstrează în continuare şi azi (decembrie 2020), când la radio se aud evocări cu ocazia împlinirii a 31 de ani de la Revoluţia din decembrie 1989. Şi acum elevii trăiesc impulsul de a se refugia în această “stare de ghiocel” ca să nu atragă atenţia asupra lor iar profesorul să-i întrebe ceva din lecţie (la multe lecţii se întâmplă aste, chiar la multe materii, dar acesta este un alt subiect).

Haideţi să schimbăm punctul de vedere din cel particular într-unul cât mai general. Haideţi să aruncăm o privire în trecut, asupra respectivei părţi a geometriei în spaţiu, să vedem cum stăteau lucrurile la nivel naţional într-un trecut cât mai îndepărtat, cât mai “istoric” posibil. Ar fi minunat să putem afla de unde vine această ordonare a materiei. Sursele mele de informare sunt în acest punct deosebit de limitate, dar câte ceva tot am găsit (oare nu se apucă nimeni de o cercetare mai profundă a acestui subiect?).

În perioada interbelică şcoala (cât de cât) obligatorie era de 4 ani. Doar cei aleşi de soartă mergeau mai departe la liceu. Pentru aceste elite exista o materie mult mai intelectuală decât ar fi fost normal în cazul unei şcoli de masă. Odată cu extinderea învăţământului de masă de către autorităţile comuniste, mai întâi la 7 clase, apoi la 8, a fost nevoie de adaptarea materiei obişnuite din primele clase de liceu (actualele clase 5-8) la o formă cât de cât accesibilă întregii populaţii şcolare. Aici autorii de manuale s-au confruntat cu o mare dilemă, anume cum să adapteze o materie setată de ani buni doar pentru elite într-o formă folosibilă pentru “tot poporul”, cerută de către noile autorităţi, care puneau populaţia muncitoare deasupra elitelor intelectuale.

Mergând în urmă pe această “linie de studiu”, am avut norocul să-mi parvină un manual semnat A. Hollinger din 1957: GEOMETRIA Manual pentru clasa a VII-a, Ed. de Stat didactică şi pedagogică. Cartea este împărţită în două părţi: GEOMETRIE PLANĂ şi GEOMETRIE ÎN SPAŢIU. Prima parte are şase capitole: I. Figuri asemenea; II. Relaţii metrice într-un triunghi dreptunghic; III. Elemente de trigonometrie; IV. Poligoane regulate; V. Ariile poligoanelor; VI. Lungimea şi aria cercului. A doua parte are două capitole: VII. Introducere; VIII. Arii şi volume. Iată în detaliu cuprinsul părţii a doua:

Bănuiesc că acest manual este din anii când şcoala obligatorie din România fusese extinsă de la 4 ani la 7 ani, deci era manualul de geometrie pentru ultimul an de şcoală generală. Vedem cum şi atunci autorii de manuale considerau ca obligatoriu – din punct de vedere ştiinţific – un studiu preliminar despre drepte şi plane în spaţiu, studiu care să pregătească înţelegerea corpurilor. Pare o obsesie a matematicienilor, care oarecum nu ţine cont de existenţa intuiţiei naturale a elevului (intuiţie cu care însă lumea matematicienilor constatase că s-a păcălit rău de tot în cazul situaţiei sistemului geometric axiomatic, pe la începutul secolului al XIX-lea, aşa încât de-atunci a început “să sufle şi-n iaurt”, adică să ţină cont destul de obsesiv de aceasta chiar din şcoala elementară). Pe de altă parte putem vedea lucrurile şi astfel: în general, în perioada postbelică, corpurile geometrice erau mult mai puţin prezente în viaţa elevului de rând, decât sunt acum. De pildă, în prezent orice copil de şcoală primară a văzut cuburi Rubik sau poze şi filme cu piramidele din Egipt, pe când în anii postbelici “cultura generală” a elevilor despre corpuri geometrice trebuie că era mult mai redusă. Dar să revenim la manualul din 1957.

Capitolul VII. de introducere în geometria în spaţiu nici măcar nu are un titlu, dar nu are trecute la cuprins nici titlurile lecţiilor, deşi dacă răsfoim prin carte găsim nişte titluri (un fel de titluri de aliniat): 139. Planul; 140. Determinarea planului; 141. Poziţia unei drepte faţă de un plan; 142. Construcţia unei drepte paralele cu un plan; 143. Poziţia relativă a două drepte; 144. Drepte paralele; 145. Unghiul a două drepte; 146. Poziţia relativă a două plane; 147. Plane paralele; 148. Dreaptă perpendiculară pe un plan; 149. Condiţia ca o dreaptă să fie perpendiculară pe un plan; 150. Distanţa dintre două plane paralele; 151. Proiecţii; 152. Perpendiculare şi oblice; 153. Distanţa de la un punct la un plan; 154. Unghiul unei drepte cu un plan; 155. Unghi diedru; 156. Unghi plan corespunzător unui unghi diedru; 157. Reprezentarea corpurilor prin desen cotat (tipărită cu caractere mai mici); 158. Reprezentarea corpurilor în perspectivă; 159. Exemple (pătrat, triunghi echilateral, hexagon regulat reprezentate “culcat”).

Titlul 157. are o clară utilitate tehnică (eram în anii de foc ai comunismului, iar absolvenţii care aveau să intre după şcoală în câmpul muncii trebuiau să primească primele indicaţii pentru citirea unui desen tehnic în vederea confecţionării unei anumite piese). Tilurile 157 şi 158 sunt de fapt împreună şi prezintă instrucţiuni detaliate de reprezentare a figurilor şi corpurilor în spaţiu (din păcate, după titlul 158. mai aparte un exemplu de la titlul precedent). Lecţia cuprinsă în aceste două titluri este foarte bine explicată şi actuală oricând.

Este de bănuit ca acest capitol VII. introductiv în ale geometriei în spaţiu să fi fost oricum parcurs “pe repede înainte”, deoarece toată partea de geometrie în spaţiu ocupa cel mult jumătate din anul şcolar, mai probabil însă sub jumătate (poate că cele două capitole aveau alocat doar trimestrul III.). Pentru a înţelege diferenţa uriaşă existentă între acestă prezentare introductivă şi actuala formă a materiei din semestrul I al clasei a 8-a, am anexat în final în scanare acest capitol. Se vede clar cum prezentarea este setată totalmente pe o cunoaştere intuitivă, puţinele cazuri de “teoreme” primind această denumire doar ca “titlu ştiinţific-nobiliar”.

Putem privi importanţa dată celor două părţi ale geometriei în spaţiu şi analizând pur şi simplu numărul de pagini alocat fiecăriua: Cap VII. Introducere are 19 pagini, pe când Cap. VIII. Arii şi volume are 34 de pagini. Cei drept că apar ocazional şi corpuri neregulate (din punct de vedere a bazelor). Nu l-am studiat în detaliu, dar nu am văzut figuri cu corpuri înclinate. Ca o observaţie evidentă, actualmente raportul între cele două părţi este cu totul altul (cam invers).

Sare “în ochi” destul de repede faptul că nu apare teorema celor trei perpendiculare. Din păcate nu am în paralel spre analiză şi manualul pentru primul an de liceu (sau pentru al doilea), unde este de aşteptat să apară totuşî această vestită teoremă, dar faptul în sine ne arată că aceasta era privită ca un element de geometrie teoretică “înaltă”, doar pentru “cei aleşi” (cei capabili de aşşa ceva şi care intrau la liceu).

Desigur că mai trebuie să ţinem cont în analiza noastră şi de faptul că la vremea respectivă se mergea la şcoală cam de la 6 ani împliniţi, clasa I corespunzând actualei clase pregătitoare, astfel încât acest manual de clasa a 7-a corespunde ca vârstă adresată actualei clase a 6-a.

Revenind la capitolul analizat, putem compara situaţia de atunci cu situaţia actuală şi din punct de vedere al problemelor. Dacă veţi avea răbdare să le lecturaţi, veţi constata că sunt probleme pe bază de situaţii din lumea înconjurătoare, “probleme” ce scot în evidenţă situaţii din lumea reală bazate pe teoria studiată. Nici vorbă de problemele cu care suntem obişnuiţi la ora actuală, deşi se pot găsi anumite probleme ce ar merita făcute la clasă.

Legat de capitolul despre corpuri, merită făcută o singură observaţie: vedeţi cum cilindrul este făcut imediat după prisme, fiind de fapt asimilat grupului prismelor; cilindrul este de fapt o prismă cu baza cerc, simplu, nu-i aşa? Dar, oare, ce-i acela un prismatoid? Nu vă bateţi capul, e o ciudăţenie, lecţia conţinând şi anumite elemente profund discutabile.

Haideţi să facem un salt în timp, tot cu A.Hollinger, dar alături de Carina Pârvulescu, la manualul de clasa a 8-a din 1971 (deja se introdusese de mult clasa a 8-a în şcoala generală, iar geometria în spaţiu avea la dispoziţie un an întreg din şcoala generală, cu materie cuprinsă în examenul de admitere la licee). Între timp capitolul ce ne interesează a primit şi un nume Drepte şi plane (e comic, dar acesta nu are şi un număr). Studiul despre corpuri, cu arii şi volume a fost despărţit în două, existând capitolul 2. Poliedre şi separat capitolul 3. Corpuri rotunde. În plus mai există şi un capitol ciudăţel cuprinzând Elemente de cosmografie (oamenii trebuiau să înţeleagă ce se petrecea în marea luptă de cucerire a spaţiului cosmic, între “minunea sovietică” şi capitaliştii ăia de americani).

Deşi se păstrează linia de prezentare intuitivă în capitolul despre drepte şi plane, între timp a apărut şi teorema celor trei perpendiculare, dar şi unele probleme de structuri artificiale constuite ad-hoc (de pildă: în figura 64 punctul M este exterior planului triunghiului ABC etc.). La acest capitol sunt cu totul 6 pagini de exerciţii scrise mai mărunt, incluzând însă şi 16 figuri generoase, cu multe întrebări din anii ’50 pentru aprofundarea fenomenelor studiate (apare din nou scăunelul cu trei picioare), dar şi probleme noi, atât dintre cele pe structuri artificiale, dar şi întrebări pe corpuri studiate (între timp capitolul foloseşte şi corpuri elementare, cuburi, prisme sau piramide).

Cum spuneam, astfel de analize ale formelor de predare din trecut ar trebui făcute în mod foarte serios, pentru că de acolo pot fi deduse idei deosebit de bune în rezolvarea problemelor cu care ne confruntăm în prezent. În general, orice programă şi orice manual vor corespunde cu adevărat nevoilor actuale doar dacă se bazează pe un studiu profund al trecutului, din punct de vedere al experienţelor de predare, apoi pe un studiu profund al prezentului, mai ales din punct de vedere al psihologiei elevului din zilele noastre, şi nu în ultimul rând un studiu profund al viitorului, din punct de vedere nevoilor generale ale viitorilor adulţi pe toate palierele profesionale posibile, adică pe tot evantaiul profesional, dem la cei de orientare reală la cei de orientare umanistă, de la cei de elită până la muncitorul de rând (care, şi acesta, ar trebui să înveţe să gândească la nivelul său de capacitate şi de nevoi).

Din păcate, fiecare pas făcut în reformarea predării matematicii, pas care nu ţine cont de aceste aspecte, trimite tot mai departe în viitor o posibilă vindecare a predării geometriei pentru generaţiile următoare. De pildă, analizând o culegere pregătitoare cu teste pentru noua formă de Evaluare Naţională în finalul clasei a 8-a (una renumită, “nu spui care”), observ că elementele de stereometrie sunt aproape eliminate, preluând de la sine înţeles (drept “cvasi-obligatorie”) ideea din anul trecut şcolar când aria şi volumul corpurilor au fost excluse din programa de examen. Oameni buni, ce facem aici? Distrugem generaţii după generaţii! Constantin Titus Grigorovici

P.S. Pe când erau gate părţile 7 şi 8 ale acestui mega-eseu, discutând pe aceste subiecte cu soţia mea, a reieşit un aspect special. Ea şi-a adus aminte cum în clasa a 8-a savura situaţii de tipul unor piramide neregulate, adică la care fie baza este un poligon neregulat (cel mai uzual exemplu este un romb) dar înălţimea cade în centrul acestuia, fie că înălţimea cade într-un punct necentral al bazei (eventual chiar într-un colţ al bazei), fie amândouă cumulate. La aceste corpuri trebuia să calculezi înălţimile feţelor laterale în mod special, acest calcul implicând de obicei şi aplicarea teoremei celor trei perpendiculare, această mare teoremă căpătând astfel un sens practic, pe mintea elevului de clasa a 8-a (care tot în scopul calculării găseşte o justificare mai pe mintea lui, decât în scopul demonstrării pure a unor situaţii – vorbesc aici de amintiri rămase de 40 de ani, însă în mintea unui profesor).

Bine, veţi spune, dar corpurile neregulate nu sunt actualmente în materie. Da, pentru că au fost scoase din materia clasei a 8-a cândva la începutul anilor ’90, exact ca să uşureze materia. Dar nu au uşurat-o, pentru că toate aceste aplicaţii ale teoremei celor trei perpendiculare au fost păstrate în probleme pe structuri artificiale: Pe planul rombului ABCD se ridică perpendiculara OM, O fiind punctul de intersecţie al diagonalelor rombului etc. Problema a rămas, dar a fost de fapt crescut nivelul de dificultate, deoarece elevul nu mai are corpul care să-i ofere acea “schelă” de susţinere a imaginaţiei şi a gândirii în spaţiu.

Ah, da, şi am omis un aspect: vorbesc aici de amintirile unui fost elev care în clasa a 8-a a ratat “la mustaţă” locul 1 la olimpiada judeţeană pe Cluj (pe-atunci acesta era apogeul, ne-existând şi fază naţională). Soţia mea povesteşte cum savura munca de a depista unde cade respectiva “apotemă”; teorema celor trei perpendiculare căpăta astfel “sens” în mintea sa. Şi eu am astfel de amintiri, puţine însă din clasa a 8-a (eu n-am umblat la olimpiade în a 8-a), dar multe din liceu (care evident predomină).

Reversul acestei situaţii, anume calculul ariei laterale a unor piramide regulate, ne atrage din nou atenţia asupra unui aspect special, anume asupra faptului că la apotema piramidei regulate nu este nevoie de T3P. Nu este nevoie, după mintea elevului de a 8-a, dar nu este nevoie nici din punct de vedere teoretic, feţele laterale ale piramidei fiind triunghiuri isoscele, în care înălţimea cade evident în mijlocul muchiei de bază, toate calculele putând fi efectuate cu cunoştiinţele de a 7-a. Cu alte cuvinte, reiese iarăşi aspectul de care am scris, anume că pentru aria laterală a unei piramide regulate (a piramidelor din programă) nu este nevoie de T3P, în general de  toată partea de teoreme în spaţiu.

Am alunecat din nou în această stare pe care unii ar putea-o interpreta drept agresiune la adresa rigurozităţii matematice. Nimic mai greşit! Problema este în cu totul altă direcţie: rigurozitatea matematică este foarte importantă, dar locul ei în forma pură este altundeva, anume în facultate, deci după o a doua selecţie a doritorilor de matematică (prima fiind la sfârşitul clasei a 8-a). După prima selecţie se poate trece la rigurozitate ridicată, dar nu absolută, aspectele de psihologia pedagogică trebuind să rămână activă în selecţia materiei (chiar dacă nu pe primul loc, ci doar pe al doilea, după rigurozitatea teoretică). Înainte de prima selecţie a populaţiei şcolare rigurozitatea matematică trebuie să fie însă pe al doilea loc, după criteriile psiho-pedagogice. Până la EN din clasa a 8-a, fiind o şcoală generală, matematica trebuie să aibă ca obiectiv principal formarea şi şcolirea capacităţii de a raţiona la cât mai mulţi elevi, nu doar la elite. Şcolirea gândirii trebuie adaptată la nivelul marii populaţii şcolare. O gândire prea ridicată în cadrul orelor de matematică îi lasă pe cei mai mulţi fără o gândire raţională (adică îi lasă proşti!).

Bine, dar cum facem cu rigurozitatea teoretică a geometriei, care este astfel condamnată “să rămână de căruţă”, pentru că geometria sintetică se mai face doar în clasele gimnaziale? Aici iese în evidenţă marea gafă petrecută la reforma din 1997 când a fost scoasă geometria sintetică din licee, după ce la reforma din 1980 se cam înghesuise oricum toată la un nivel foarte înalt în gimnaziu. Practic, după 1980 se făcea geometria sintetică de două ori, cam la fel (în cazul generaţiilor care au terminat clasa a 8-a înainte de 1981 geometria gimnazială era la un nivel mai scăzut decât cea din liceu). Astfel, în 1997 s-a considerat că de fapt nu-şi mai are loc o a doua reluare a geometriei sintetice în liceu, pentru că aceasta oricum se face în mod complet în gimnaziu. Aici este MAREA GREŞEALĂ, despre care nu ştiu cât este de clar sesizată la nivelul conducerii matematicii româneşti.

Acum ne pregătim pentru o nouă programă de liceu (generaţia ce a pornit prima clasa pregătitoare este în clasa a 8-a iar pentru ei trebuie făcut totul nou), dar pandemia ne ocupă tot timpul şi parcă văd că ratăm şi acest moment ce ar putea fi reparatoriu la adresa geometriei. Pentru mine este evident că acesta ar trebui să fie cât mai urgent subiectul unui viitor eseu (dacă nu m-am trezit prea târziu).

SCANARI Cap VII-Introducere

Am ajuns la capătul unui drum explicativ deosebit delung, dar şi detaliat, de înţelegere a contextului în care se integrează “geometria de calculat” alături de “geometria de demonstrat” în şcolile noastre gimnaziale. În acest sens am explicat de la început că întregul fenomen trebuie înţeles în toată amplitudinea sa, din toate punctele de veddere, iar fenomenul trebuie adaptat în funcţie de diferitele situaţii întâlnite.

Situaţia actuală este rezultatul mai multor reforme, cea mai nocivă fiind pe departe reforma din 1980, cerută la vremea respectivă de Ceauşescu, numită de mine “reforma uitată” pentru că majoritatea profesorimii a uitat de aceasta şî despre cum arăta matematica şcolară până la finalul anilor ’70.

Actualmente, începând cu noua programă din 2017 s-au încercat paşi reparatorii destul de puternici, dar profesorii de matematică nu-i înţeleg. Din partea oficialităţilor nu s-a făcut destul încât să “se întoarcă căruţa” înspre o direcţie mai sănătoasă (nu am discutat despre cauzele acestei situaţii sau despre ce ar fi trebui făcut).

În acest sens reiau un singur exemplu din câte am discutat: chiar zilele acestea, după publicarea părţii (4) a acestui mega-eseu, m-am întâlnit din nou cu o situaţie absurdă şi am promis că o voi prezenta. Este vorba despre capitolul de arii din clasa a 7-a, în care, la propunerea unui elev de a rezolva cu teorema lui Pitagora, profesorul spune ad-literam: încercăm să evităm folosirea lui Pitagora. Este NOAPTEA MINŢII să lucrezi întreg acest capitol fără teorema lui Pitagora, deşi de data asta elevii o cunosc din finalul clasei a 6-a, doar aşa, pentru că tu te-ai obişnuit să-l predai fără Pitagora şi îţi este greu să te schimbi.

Poate onor cititorii au simţit, poate nu, dar merită să precizez un aspect important: am redactat întreg acest mega-eseu cu durerea în suflet că în România planimetria şi stereometria sunt neglijate, fiind clar pe un loc secund după geometria axiomatică, cu definiţii şi demonstraţii, cu multe multe demonstraţii, care însă sunt accesibile doar unei minorităţi a populaţiei şcolare. Am încercat să aduc argumente înspre alegerea unei căi de echilibru (nu vreau să pun “prostimea” în faţă, ci doar să avem un echilibru între atenţia dată elitelor şi atenţia acordată marii majorităţi a populaţiei şcolare).

Dar ce m-a apucat chiar acum? Totul a fost motivat de experienţa de anul trecut, experienţă ce pare să se repete în mod stupid, prin care – printr-un simplu ordin de ministru – a fost ştearsă din viaţa unei întregi generaţii toată stereometria din clasa a 8-a.

Să analizăm, deci, – din nou (a nu ştiu câta oară, poate mă şi aude totuşî cineva) – să analizăm ce s-a întâmplat după declanşarea pandemiei de Covid-19 din punctul de vedere al sterometriei. În primul rând să ne aducem aminte cum a fost tratată situaţia de către ministerul condus de D-na Anisie pentru generaţia clasei a 8-a din anul şolar 2019-2020. Păi, simplu: s-a decis, prin analogie cu materia de la Limba şi literatura română, să se taie materia de examen la finalul semestrului I (orientativ), astfel încât materia de arii şi volume a fost eliminată de la examen, lăsată pur şi simplu “pe din afară”. În paralel, şi-au dat ei seama că au o problemă mare cu cei care nu pot “duce” demonstraţii, aşa că au introdus acele cerinţe înjositoare, restrângând întrebările de planimetrie la nivelul clasei a 5-a, iar stereometria desfiinţată cu totul (cu excepţia determinări de lungimi bazate tot pe demonstraţii grele în spaţiu).

Nici nu mai are rost aici să discutăm că aceşti elevi, odată împrăştiaţi la diferitele forme de şcolarizare în clasa a 9-a nu vor mai relua niciodată stereometria, deşi D-na Ministru aşa a promis (că să stea liniştiţi părinţii, că materia se va relua la toamnă). Cu alte cuvinte, vom avea o generaţie care habar nu are de paşii minimali de calcul practic a ariilor sau a volumelor. Minunat! Bine însă că cei puţini care pot înţelege au parcurs liniştiţi mai toate formele de demonstraţii în spaţiu. Încă o dată precizez: “MINUNAT”!!!

Haideţi să vedem cum stau însă lucrurile pentru generaţia următoare (clasa a 8-a pe anul şcolar 2020-2021). Pentru că, ne-am fi aşteptat să se remedieze lucrurile măcar pentru aceştia, adică ne-am fi aşteptat ca responsabilii cu matematica să fi sesizat situaţia şi să fi încercat într-o formă sau alta să prevină repetarea acesteia la următorii elevi de a 8-a. Am avut totuşi o vară în care se puteau studia lucrurile, astfel încât la reîntoarcerea la şcoală să fim întâmpinaţi cu “o programă de pandemie” orientativă (un “plan B”, în caz că se întâmplă din nou să se închidă şcolile), măcar pentru clasele terminale (faceţi prioritar aia şi aia, lăsaţi mai la coadă acelea etc., în caz că vom trece iarăşi în online, că acum sunteţi pregătiţi cu calculatoare şi cu tablete …). Dar nu, nu s-a făcut nimic, totul sub premisa tâmpită: “hai să fim optimişti!”.

De-abia după o nouă închidere a şcolilor s-a trezit şi D-na Ministru şi a dat ordin să se facă “o programă de avarie”. Când va apărea aceasta? Pentru că, până una-alta, profesorii merg mai departe pe programa oficială şi bagă de zor poziţii relative ale dreptelor şi planelor. Iar vor rămâne pe de lângă calculele simple, dar neumilitoare de arii şi volume implicând şi teorema lui Pitagora? Ne putem aştepta. Mai sacrificăm o generaţie, pentru că oricum, din punctul de vedere al unui filolog “se face prea multă matematică în România”.

Putem pune şi altfel problema: cât poate dura să se facă o “programă de avarie”? Chiar nu s-a gândit nimeni până în toamnă la aceste aspecte şi la o astfel de posibilitate? Groaznic! Acum oricum se schimbă tot guvernul; cine ştie când se va face, dacă se va mai face o astfel de programă de “planul B”.

În aceste condiţii, cel mai bine ar fi să se lase aşa cum sunt, dar să se lase şi toată materia pentru examen. În aceste condiţii lucrurile vor putea fi reglate de la sine – fiecare va face cât poate de mult, ordonându-le după posibilităţile concrete – iar din partea ministerului vor veni noi teste de antrenament cuprinzând şi calcul de arii şî volume, măcar pe corpurile esenţiale, cele care apar şi în practică (incluzând şi corpurile rotunde simple). Deci, stimaţi conducători ai matematicii şcolare româneşti: nu mai scoateţi de la EN calculul de arii şi volume!

Apropos, în toamnă au fost sistate pentru acest an şcolar şi olimpiadele, aşa că oricum toată geometria demonstrativă din materia olimpiadelor este cam degeaba. Ba nu, veţi spune, rămâne totuşi pentru examen. Da, voi răspunde eu, este pentru examen, dar accesibilă doar unei minorităţi reduse. Cu restul ce facem??? Păi, vă zic eu ce facem: îngroşăm rândurile analfabeţilor funcţionali la următoarele studii PISA, iar de data asta o facem ordonat şi cu reluare; nu cu premeditare, dar din prostie şi cu indiferenţă. Constantin Titus Grigorovici

P.S. V-am obişnuit la părţile acestui eseu să am şi alte comentarii colaterale şi nici acum nu fac excepţie. Nu pot să nu mă gândesc la acţiunea mediatizată (dar, din păcate, prea puţin luată în seamă) a colegului Sorin Borodi din Dej, care prin 2019 s-a revoltat puternic pentru faptul că elevii nu ştiu să aplice matematica învăţată în situaţii din viaţa reală.

Atât planimetria, cât mai ales stereometria sunt domenii matematice care sunt potrivite “par excellence” ca domenii de aplicabilitate în viaţa de zi cu zi. Din clasa a 5-a se pot da elevilor probleme cu volumul şi aria unui acvariu sau a unei piscine paralelipipedice, iar în clasa a 8-a ar trebui să facem din nou şi aplicaţii pe diferite corpuri, cutii de carton sau alte obiecte cât de cât realiste.

Desigur că ultima precizare este esenţială, anume că trebuie să fie o situaţie realistă, iar elevii simt imediat o situaţie dacă aceasta este cu totul falsă. Mi-a rămas în memorie un contra-exemplu năucitor dintr-o culegere din urmă cu câţiva ani (citat orientativ din memorie): în figura alăturată este reprezentat un tort în formă de piramidă patrulateră regulată cu vârful în jos … Pe bune? Ce a gândit acel coleg când a redactat respectiva problemă? Şi, nu s-a gândit nimeni să-l tragă niţel de mânecă?

Vă las pe dvs. să trageţi concluziile acestui Post Scriptum din punct de vedere al faptului că ministerul “se cam joacă” de-a scosul stereometriei din clasa a 8-a pentru al doilea an la rând. Adică, ce vreau să zic? Păi, nici măcar nu am avut vreun ordin care să ceară explicit profesorilor de la clasele de a 9-a să recupereze fiecare cum s-o pricepe, măcar pentru câteva ore, pe câteva exemple, partea de stereometrie din clasa a 8-a de anul trecut (proces care să fie finalizat cu un scurt test, pentru o minimă garanţie). În schimb, vedem cum “istoria” pare să se repete şi anul acesta şcolar, pentru următoarea generaţie.

Am parcurs acest drum explicativ deosebit de detaliat, dar şi lung, pentru a înţelege contextul în care se petrece “geometria de calculat” în şcolile gimnaziale din România. În acest sens am explicat de la început că întregul fenomen trebuie înţeles în toată amplitudinea sa, din toate punctele de vedere, prezentând în acest sens trei “axe de discuţie”, pe care le reiau aici pe scurt: 1) axa calcule – demonstraţii; 2) axa 2D – 3D; 3) axa pedagogie – ştiinţă.

Am văzut astfel în acest mega-eseu cum se alternează parcurgerea şi abordarea materiei, pendulând de-a lungul acestor axe într-un fel destul de discutabil, de multe ori deosebit de agresiv la adresa nevoilor şi a posibilităţilor elevilor la diferite vârste. Multe se mai pot înţelege cumva, dintre cele ce se întâmplă în clasele 5-7, dar agresivitatea sistemului la adresa elevilor de rând îşi atinge apogeul în geometria de clasa a 8-a. Vorbesc aici de ordinea total nepedagogică între partea de demonstraţii cu “teoreme în spaţiu” şi partea de stereometrie, adică de calcul a ariilor şi a volumelor diferitelor corpuri studiate. Să analizăm acest subiect.

Materia este aranjată după principiul rigurozităţii mtematice absolute al ordonării materiei, anume că un elev nu ar putea lucra pe corpuri până nu a studiat pe deplin toate situaţiile ce pot apărea între drepte şi plane în spaţiu. Această abordare neagă însă intuiţia elevilor (câtă o mai fi ea acolo, în mintea lor, după trei ani de predare care le-a îngrădit-o cu totul). Prin eseul de faţă, însă, susţin punctul de vedere opus, anume că se poate studia cea mai mare parte a stereometriei, adică a calculului de arii şi volume pe corpurile regulate de bază, înainte de a studia poziţiile şi “comportamentul” dreptelor şi a planelor în spaţiu.

Unele elemente din stereometria de clasa a 8-a se repetă din clasa a 5-a (când au fost predate intuitiv), iar ariile diferitelor figuri se cunosc bine din clasa a 7-a (plecăm de la premisa că elevii, cumva le-au învăţat totuşi până la intrarea în a 8-a). Calculul de arii şi volume reprezintă o parte de materie accesibilă marii majorităţi a elevilor, abordabilă intuitv şi prin analogie cu unele anterioare, pe când demonstraţiile în spaţiu nu sunt accesibile decât copiilor de vârf. Aranjarea materiei astfel încât pe întregul semestru I se parcurge o materie acesibilă doar elitelor, aceasta este o agresivitate năucitoare la adresa celor 80% dintre elevi care nu pot, sau nu au nevoie, sau nu-i ineresează demonstraţiile în spaţiu. Şi apoi ne mirăm că aceştia clachează masiv la diferite teste! Păi, dacă îi ţinem în şcoală cu o materie pe care nu o înţeleg, care se adresează altora ce să ne aşteptăm? Singurele urmări clare sunt cele de ordin psihologic, cum ar fi frustrarea, agresivitatea, refuzul matematicii de orice fel etc.

Parcurgerea în 3D a axei calcule – demonstraţii dinspre acestea din urmă un semestru întreg, ajungând la calcule de-abia în semestrul al II-lea, această ordine a materiei sfidează masiv cerinţele pedagogice, prin faptul că dă întâietate ştiinţei pe axa pedagogie-ştiinţă, deşi la vârstele gimnaziale prioritare ar trebui să fie principiile pedagogice (vezi P.S. în final).

Pot întreba aici şi altfel: cât la sută din populaţia şcolară va ajunge să facă ştiinţa matematică? Răspunsul l-a dat George Pólya: 0,1%, cu extindere la 1% pentru toţi cei care vor avea colateral nevoie de matematică ca ştiinţă. Ok, poate lucrurile au mai evoluat de pe vremea lui Pólya, dar oricum nu au cum să treacă de 10% din populaţia şcolară. Pentru aceşti 10%, în numele unei rigurozităţi ştiinţifice matematice stupide, noi îi sacrificăm pe restul populaţiei şcolare, iar apoi, ca să nu se vadă situaţia profund dezastroasă, le dăm să calculeze aria unui dreptunghi la examen (pe care le dăm şi “de-a moaca” 5 puncte, cerinţă la care le dăm şi răspunsul “pe faţă” (Arătaţi că aria dreptunghiului ABCD este egală cu 240 cm²).

Se poate şi altfel? Oare se poate găsi o formă de geometrie care să nu-i lase “pe de lângă” pe cei mulţi? Se poate găsi o formă de predare şi o ordine a lecţiilor prin care să dăm mai întâi materia practică şi accesibilă celor mulţi, cei care au nevoie de mai mult timp ca să înţeleagă o lecţie (poate luni întregi), iar doar apoi să trecem la lecţiile mai grele, mai teoretice, pentru cei capabili a le înţelege, dintre care se aleg de fapt participanţii la concursurile şcolare de elită (iar aceştia să apuce să le înveţe până la olimpiadele din februarie-martie), se poate aşa ceva? Se poate preda geometria mergând de la uşor la greu, de la accesibil la dificil, respectând astfel unul dintre principalele principii psihopedagogice? Da! Se poate!

Iată cum predau eu de peste 20 de ani geometria clasei a 8-a, îmbinând cerinţele psihopedagogice elementare cu cerinţele minimale de rigurozitate a matematicii. În linii mari parcurg trei părţi pentru geometria în spaţiu de clasa a 8-a. Cap. 1): un prim calup de corpuri studiate pe rând (prismele şi piramidele), parcurse intuitiv îi dau elevului “o schelă de sprijin” pentru activitatea geometrică în spaţiu. Cu acest capitol încep geometria de clasa a 8-a, chiar în septembrie. Cap. 2): un studiu structurat al geometriei dreptelor şi planelor în spaţiu. Acest capitol ocupă partea a doua a semestrului I, terminându-se înainte de vacanţa de iarnă sau cândva în ianuarie. Cap. 3): un al doilea calup de corpuri studiate pe rând (trunchiurile de piramidă şi corpurile rotunde), parcurse pe formatul deja cunoscut, incluzând şi “marile demonstraţii” ale stereometriei (volumul trunchiului de piramidă, aria laterală a conului şi volumul şi aria sferei). M-am obişnuit să parcurg acest capitol pe cât posibil după simularea oficială din martie, dar îl termin obligatoriu până la vacanţa de Paşte, pentru ca elevii să aibă timp suficient a se pregăti pe teste generale. În continuare doresc să descriu pe rând pe fiecare din aceste trei capitole

Cap. 1): La fiecare corp facem desenul, descrierea elementelor (vârfuri, muchii, feţe) şi deducem raţional, prin problematizare, ariile şi volumul, cât şi diverse lungimi speciale. Când avem nevoie de teorema lui Pitagora, susţinem raţional perpendicularitatea pe baza faptului că un segment vertical din figură este perpendicular pe un segment orizontal pe care cade. De exemplu, muchia verticală DD’ a unui cub este evident perpendiculară pe diagonala BD a bazei, care este orizontală. Prin astfel de justificări elevul învaţă să vadă unghiurile drepte în spaţiu, deşi în reprezentările grafice are loc o deformare a acestora.

Iată încă un exemplu de unghi drept uşor de justificat fără nici cea mai mică teoremă în spaţiu: segmentul VM care uneşte vârful unei piramide patrulatere regulate cu mijlocul muchiei BC (adică o mediană) este perpendicular pe BC pentru că triunghiul VBC este isoscel (oricum, nici abordarea oficială nu este mai riguroasă). Teorema celor trei perpendiculare în cazul determinării apotemei îşi găseşte sensul doar în cazul unei piramide neregulate (de ex. o piramidă cu baza romb şi înălţimea ridicată în intersecţia diagonalelor acestuia), dar aceste oricum nu mai sunt în materie de peste un sfert de secol.

Ordinea în această primă parte este stabilită având criteriul accesibilităţii intuiţiei elevilor ca punct central, şi este următoarea: cubul; paralelipipedul dreptunghic; prisma patrulateră regulată şi prisma triunghiulară regulată predate în paralel, apoi piramida patrulateră regulată, iar în final, predate în paralel piramida triunghiulară regulată şi tetraedrul regulat. Alt criteriu ce susţine această ordine îl reprezintă accesibilitatea calculului; pe copii îi atragi de partea matematicii dacă le prezinţi la început elemente accesibile, crescând doar ulterior nivelul.

În această primă parte facem multe exerciţii de calcul cu teorema lui Pitagora, cu rezultate întregi sau iraţionale, dar şi multe desene colorate în care elevii au de trasat şi de colorat diferite secţiuni în corpuri. Mă refer aici în primul rând la secţiunile particulare în cub (secţiunile diagonale, cele paralele cu feţele, dar şi secţiunea triunghi echilatera), sau în piramida patrulateră regulată (secţiunile diagonale). Elevii au astfel ocazia, chiar sarcina, să deseneze multe astfel de corpuri cât mai corect şi să facă pe acestea multe calcule (adică stereometrie). În această fază geometria se desfăşoară doar în corpurile studiate, luate ca structuri întregi. Începând din acest capitol, elevii de rând au de lucru, urmând să acumuleze experienţă şi abilităţi sigure de desen şi calcul pentru lungimile, ariile şi volumele studiate aşa că ne putem ocupa de materia pentru cei buni.

Cap. 2): De-abia după ce elevii s-au obişnuit cu desenele şi cu vederea în spaţiu, de-abia apoi trecem la studiul dreptelor şi a planelor în spaţiu; acum putem trece la un studiu cât de cât pregătit al elementelor demonstrative. Primele 2-3 ore discutăm despre notaţii, convenţii de desen, determinarea planului, faptul că unghiurile par deformate în spaţiu, discutăm despre dreptele necoplanare şi despre multe alte aspecte ce trebuie acum conştientizate.

Din punct de vedere a sarcinilor de lucru ce pot fi întâlnite în probleme, facem o structurare a “teoremelor în spaţiu”, practic a reţetelor de demonstrare a diferitelor situaţii, organizate după două principii. În primul rând avem principiul poziţiei relative, care include trei poziţii relative: paralelismul; unghiul relativ, respectiv determinarea măsurii acestuia, şi situaţia de perpendicularitate relativă. În al doilea rând avem principiul obiectelor poziţionate: astfel, trebuie să studiem poziţia relativă a două drepte, apoi a unei drepte faţă de un plan, iar în final poziţia a două plane. Avem astfel 9 situaţii de studiu, plus teorema celor trei perpendiculare, pe care le enumăr în continuare în ordinea în care le parcurg cu elevii (de la cele mai accesibile la început, spre cele mai complicate în final): două drepte paralele; unghiul dintre două drepte necoplanare; perpendicularitatea a două drepte necoplanare; dreaptă perpendiculară pe plan; două plane perpendiculare; dreaptă paralelă cu plan; două plane paralele; teorema celor trei perpendiculare; unghiul dintre o dreaptă şi un plan; unghiul diedru. În măsura timpului şi a interesului, parcurg şi alte teoreme necuprinse în această listă.

La fiecare astfel de lecţie facem figura teoretică de bază (eventual cu folosirea culorilor pentru a evidenţia diferite aspecte importante) şi deducem prin problematizare reţeta de demonstrare, după care dăm de obicei exemple tot în corpurile studiate. Consider că este mai bine aşa pentru că fiecare lecţie nouă este aplicată într-o zonă de confort, anume în corpurile deja cunoscute. Astfel evit introducerea mai multor informaţii noi, pe lângă cea principală într-o lecţie. De abia la teorema celor trei perpendiculare încep şi cu probleme în structuri artificiale, de tipul: pe planul dreptunghiului ABCD se ridică perpendiculara AM etc. Pe aceste două “plane de lucru” ne concentrăm atenţia pentru o vreme, până spre primăvară. Elevii de rând exersează stereometria, cei capabili au de făcut şi demonstraţiile în spaţiu.

Cap. 3): În primăvara clasei a 8-a parcurgem şi al doilea calup de corpuri, acoperind toată gama acestora ce ar putea veni la examen conform programei. Ori înainte, ori acum integrez aici şi prisma şi piramida hexagonală regulată, dar în principal avem de studiat trunchiurile de piramidă şi corpurile rotunde. Cu asta se termină ca lecţii geometria de clasa a 8-a.

Simţiţi acum că o astfel de ordonare a materiei oferă elevilor studiul geometriei pe o pantă mai lină a dificultăţii, lăsând la nivelul fiecărui elev până la ce nivel de dificltate să urce fiecare, în funcţie de posibilităţi şi interes. O astfel de parcurgere nu-i înjoseşte pe elevii de nivel mediu, adică pe majoritatea popula tiei şcolare, ci îi lasă să urce fiecare după cât poate până în ultima clipă, înainte de examenul de Evaluare Naţională. Mă refer aici la elevii care vor putea urca mare parte din acest drum, doar că mai încet, pentru că nu sunt chiar olimpici. Aceştia au însă nevoie să pornească cu lucruri simple şi să urce într-un mod accesibil. Toţi aceştia stagnează de fapt primul semestru pe programa oficială, pentru că sunt confruntaţi cu o materie prea teoretică şi cu aplicaţii prea abstracte, ei întrând automat în stare defensivă şi de blocaj. Cei care au norocul de ore în particular întră cu profesorii de acasă într-un program de dresură, dar nu neapărat şi de înţelegere, frica şi repulsia de matematică rămânând la multi prezente.

Cam aşa arată situaţia aşa cum o percep eu în Cluj. Despre cum arată la ţară pot doar să-mi închipui (mă mai ajută diferitele reportaje ce le aud la radio – mulţumesc Europa fm!). Majoritatea elevilor de la sate vor ajunge în cel mai bun caz cel mult la un liceu tehnologic. De ce să-i ţinem blocaţi un semestru întreg în demonstraţii sterile de geometrie în spaţiu?

P.S. Am atins în această parte a eseului un aspect ce trebuie lămurit. Anume, în primul sfert al textului am scris că parcurgerea demonstraţiilor timp de un semestru întreg, înaintea calculelor de arii şi volume, care vin de-abia în semestrul al II-lea, această ordine a materiei sfidează masiv cerinţele pedagogice, prin faptul că dă întâietate ştiinţei pe axa pedagogie-ştiinţă, deşi la vârstele gimnaziale prioritare ar trebui să fie principiile pedagogice. Aici matematica din România ar trebui să ajungă la pace cu pedagogia, poziţia naturală şi normală trebuind să fie una de compromis, de echilibru pentru ambele părţi. Concret, după părerea mea, între cele trei nivele de învăţământ cu profesorii de matematică, priorităţile ar trebui să fie următoarele: în ciclul gimnazial dominante să fie principiile pedagogice; în liceele de ştiinţe şi mate-info principiile pedagogice să fie în echilibru cu principiile rigurozităţii matematice, iar în facultăţile de matematică principiile matematice să fie dominante.

S-ar putea chiar trage două grafice care să descrie importanţa (poate în procente) a fiecărui domeniu, plecând de la începutul clasei a 5-a până la finalul facultăţii. Astfel, o comisie paritară de specialişti din ambele părţi ar putea decide o politică reparatorie de felul următor: importanţa criteriilor pedagogice să scadă de la 75% la în clasa a 5-a către 25% în facultate, pe când importanţa criteriilor pur matematice să crească de la 25% în clasa a 5-a pană la 75% în facultate. Liceul ar fi desigur în zona de echilibru a acestor criterii. Desigur, aceasta este o simplă propunere, dată fără o mare şi profundă analiză, dar ideea contează.

Pentru cei care s-ar simţii “şocaţi” de o astfel de perspectivă, doresc să precizez că înaintea reformei din 1980 aşa era structurată materia. Se pot găsi multe exemple în acest sens în lucrările de specialitate despre predarea matematicii în diferitele clase şcolare sau liceale, dar am auzit (doar din relatări) şi de prezenţa criteriilor pedagogice în facultăţile de matematică din anii ’50 – ’70.

Important este că acest principiu ar trebui reintrodus în şcolile româneşti, desigur după o solidă analiză, adaptat situaţiei actuale, printr-un program naţional pe câţiva ani. Altfel, tot în starea jalnică din anii aceştia ne vom regăsi şi peste decenii.

În postarea precedentă am analizat cum pe întreg parcursul clasei a 6-a elevii vieţuiesc un adevărat embargou în direcţia planimetriei şi a sterometriei (eventual în afara recapitulării de la început şi a testărilor iniţiale). La geometrie, întreaga clasă a 6-a, chiar şi o parte din clasa a 7-a, se ocupă numai de studiul figurilor geometrice, studiu făcut doar prin prisma definiţiilor  şi a demonstraţiei geometrice. Acest studiu are încă – şi actualmente, după atâtea reforme “de accesibilizare” – are încă forma de bază teoreticist-axiomatică, cu definiţii riguroase şi inaccesibile marii majorităţi a elevilor. Intuiţia, care este singura formă de înţelegere la majoritatea elevilor, intuiţia nu este accesată mai deloc (deşi conform programei din 2017 aceasta se cere explicit profesorilor). Problema este că nici profesorii de la clasă, nici autorii de manuale nu prea ştiu cum s-ar face asta, fiind prea puternic ancoraţi în forma teoreticistă ce a reprezentat normalitatea din anii ’80 încoace.

Aici se întâmplă una dintre cele mai abrutizante agresiuni la adresa majorităţii elevilor, 80-90% din populaţia şcolară nefiind încă trecută în stadiul gândirii necesar înţelegerii unei abordări abstracte a geometriei. Piaget preciza clar acest aspect, dar matematica şcolară românească este setată şi la ora actuală doar după olimpici, adică după cei foarte puţini care fac fată unui studiu abstract teoreticist al formelor geometrice, neglijându-i însă pe majoritatea elevilor. Practic, gândirea celor 80-90% dintre elevii ţării este “trasă pe line moartă”, până când se introduc toate figurile geometrice (în mod definiţionist) şi se studiază toate proprietăţile acestora (desigur, în mod demonstrativ).

Îmi permit să fac aici o întrerupere a discursului acestui eseu, pentru a relua în citat un pasaj găsit într-o carte veche din biblioteca părinţilor mei: Laboratorul de matematică (Ed. Didactică şi pedagogic, 1973), autori N. Teodorescu, Gh. N. Rizescu, B. Ionescu, D. Ogrezeanu (am întărit numele dl-ui Academician Teodorescu, pe vremuri preşedintele Societăţii de Ştiinţe Matematice din România) La pagina 5 găsim faptul că: Structura logică a minţii copilului nu este aceeaşi cu a adultului şi nu atinge stadiul adult de dezvoltare înainte de 11-12 ani. În teoria lui Piaget se menţionează mai multe stadia de dezvoltare la copii, (…) Ultimul stadiu începe după această vârstă sub numele de stadiu operaţional formal, care este un nivel adult de gândire.

Legat de această afirmaţie, părerea mea este că la mulţi copii acest stadiu apare chiar şi mai târziu, aceasta şi datorită contactului masiv încă din copilăria fragedă cu ecranul (TV, calculator, Smartphone), contact deosebit de distructiv la nivelul capacităţii de imaginaţie a unor informaţii primite pe bază de cuvinte, nu pe bază de imagini concrete,, astfel încât în ultimii 20 de ani am putut observa o maturizare tot mai lentă a tot mai multor copii.

În concluzie, părerea mea este că în clasa a 6-a actualmente este prea devreme pentru o geometrie prea matură, aşa cum încă în anii ’90 cu multe clase se putea face. Eu ţin minte lecţia de la inspecţia pentru gradul II, ţinută la Şcoala Waldorf în primăvara lui 1998 la clasa a 6-a: am definit, am dat teoremă, am calculat şi am demonstrat, iar inspecţia a fost o reuşită. Actualmente, acea lecţie o pot face doar la începutul iernii din clasa a 7-a, iar asta nu numai din motive de programă, ci şi din motivul că de-abia atunci am destui elevi dezvoltaţi astfel încât să poată parcurge această lecţie. În principiu, atât demonstraţia geometrică (în direcţia celor buni la mnatematică), cât si calculul planimetriei pe baza formulelor de arie şi a teoremei lui Pitagora (pentru toţi elevii, dar cu accent în direcţia celor medii), ambele domenii pot fi practicate în clasa a 7-a cu încredere că mulţi dintre elevii cărora ne adresăm au făcut pasul în noul tip de gândire, aşa încât vor şi fi în stare să lucreze ce le cerem.

Legat de afirmaţia dinainte, de faptul că la tot mai mulţi copii apare incapacitatea imaginării unor situaţii prezentate textual (oral sau scris), legat de aceasta mai am o observaţie colaterală. Dintr-o prezentare numerică a teoremei lui Pitagora, aşa cum cei mai mulţi profesori o fac încă, elevul va înţelege mult mai puţin decât dintr-o prezentare figurativă pe bază de arii, în care expresiile “pătratul ipotenuzei” sau “suma pătratelor catetelor” să fie adresate şi accesibile gândirii în mod dual, atât pe cale numerică (pătratul = puterea a doua), cât şi pe cale figurativă (pătratul unei laturi = aria pătratului construit pe acea latură). Fără să mai discutăm că o prezentare a teoremei lui Pitagora doar din punct de vedere aritmetico-numeric are doar darul de a prezenta această “cea mai importantă teoremă” ca o ciudăţenie matematică de neînţeles, ca un fel de “hocus-pocus”, căruia nimeni nu-i poate înţelege logica; o astfel de abordare în nici un caz nu se poate lăuda că dezvoltă gândirea elevilor.

Ca să iau o pauză din această critică în cascadă, haideţi să prezint cum abordez eu situaţia. Încercând să păstrez linia generală de introducere a figurilor geometrice înainte de a reveni la calculul de perimetre şi arii, eu mă concentrez în clasa a 6-a asupra construcţiilor geometrice, cerându-le elevilor să deseneze cu exactitate toate figurile, prin folosirea practică a diferitelor instrumente geometrice (Piaget vorbea despre stadiul operaţional concret, ca penultimul stadiu de dezvoltare). Eu accesibilizez geometria de clasa a 6-a pentru majoritatea elevilor, atrăgându-le preocuparea spre construcţia practică a figurilor geometrice, după principiul: dacă nu înţelege mai nimeni abordarea euclidiană, dar încă nu avem toate cunoştinţele pentru a face planimetrie de clasa a 7-a, atunci să cunoaştem figurile geometrice şi proprietăţile acestora prin construcţia geometrică exactă! Manualele vechi, înaintea reformei uitate din 1980 aşa aveau structurată cunoaşterea figurilor geometrice. Obsesia demonstrativă a apărut doar prin manualele din 1981.

Această abordare ajută şi în direcţia deficienţei prezentate mai sus, anume a faptului că elevii au actualmente o capacitate mult mai redusă de a-şi imagina anumite situaţii prezentate verbal. Punându-i în clasa a 6-a să se preocupe mult de desenarea concretă a diferitelor figuri, elevii vor fi în stare ulterior (adică în clasa a 7-a) să-şi imagineze diferite situaţii, pentru că au acumulat experienţe personale practice cu aceste figuri.

Dar să revenim la subiectul principal: aşadar, la nivel naţional, clasa a 6-a nu se ocupă mai deloc de subiectul planimetriei sau al stereometriei în sensul prezenţei ariilor sau a volumelor Am repetat din nou acest aspect în speranţa găsirii unor soluţii, de pildă, poate includerea unor astfel de aplicaţii în zona aritmetică a clasei a 6-a). Concret, după introducerea ariei şi a volumului ca fenomene de măsurare la sfârşitul clasei a 5-a, apare un embargou în folosirea lor, până la studierea completă prin demonstraţii a figurilor de bază, a triunghiurilor şi a patrulaterelor. De abia după studierea teoretică a acestora, adică după mai mult de un an, se revine la planimetrie (embargoul asupra stereometriei este mult mai lung, adică de doi ani şi jumătate).

Dar şi aşa, atunci când în sfârşit apar din nou ariile în viaţa elevilor (în a doua parte a semestrului I al clasei a 7-a), mare lucru nu se poate face cu formulele respective de către elevul de rând. Aplicaţiile la formulele de arie sunt puţine şi, fie sunt tembele, fie implică elemente de demonstraţii care elevului de rând nu-i sunt accesibile (de pildă, calculul ariei unui romb la care se cunosc laturile şi un unghi de 30^o – să fim realişti: câţi elevi ştiu “neavertizaţi” să aplice “cateta opusă unghiului de 30^o). Măcar dacă profesorii ar petrece mai mult timp la cele banale (tembele, cum le-am denumit aici) şi tot ar primi ceva şi copiii neolimpici, dar profesorii le consideră pe acestea înjositoare şi în general le fac în mare viteză şi nu prea le scot în evidenţă. Atâta vreme cât nu sunt folosibile pentru pregătirea olimpicilor, puţini profesori şi zăbovesc asupra lor.

La reluarea planimetriei după studiul patrulaterelor, în semestrul I al clasei a 7-a, planimetria se rezumă la prezentarea unor reţete cu care să se calculeze ariile diferitelor figuri geometrice, dar oricum, mare lucru nu se poate face apoi cu acele formule. Mai rău, cei mai mulţi profesori nici măcar nu petrec timp la căutarea prin gândire a acestor formule; acesta este în sine un proces interesant, dacă ne propunem să îl parcurgem cu elevii prin problematizare, nu printr-o simplă prezentare, dar pentru asta trebuie să fim în stare să ieşim din ordinea stupidă care începe cu aria triunghiului, apoi cândva – în altă oră – se ajunge şi la ariile patrulaterelor.

Mă gândesc să anexez prezentului eseu, ca o paranteză, o scurtă descriere despre cum ar trebui parcursă introducerea, respectiv căutarea formulelor de calcul a ariilor. Dar, oricum, fără posibilitatea folosirii teoremei lui Pitagora, planimetria se rezumă cel mult la căutarea unor reţete cu care să se calculeze ariile diferitelor figuri geometrice. Dimpotrivă, odată ce intră în joc teorema lui Pitagora, aducând cu sine posibilitatea de a determina diferite lungimi necesare în formulele de arii, viaţa elevului de rând capătă brusc mult mai mult sens.

Mă refer aici la cei cca. 80% dintre elevi, cei care au stat docil “în bancă” toată clasa a 6-a, dar mare lucru nu au dobândit la geometrie. Aceştia vor avea ocazia să înceapă şi ei a face cu adevărat matematică în momentul când ştiu să extragă un radical simplu, învaţă metoda din teorema lui Pitagora şi primesc a calcula perimetre şi arii ale unor figuri de bază. Dacă profesorul are puţin de tact pedagogic şi le dă la început câteva probleme cu soluţii naturale, ca să-i încurajeze, atunci aceştia vor prinde curaj şi vor începe să lucreze.

Ce se întâmplă însă în realitate? Din păcate, aici profesorii fac masiv gafe pedagogice, încurcându-i cât se poate de mult pe elevi şi împiedicându-i să înţeleagă geometria. Ca să nu pară din nou că arunc aici cu critici gratuite, doresc să dau câteva exemple observate printre colegii profesori, în general toţi “profesori buuuni (!)” la şcoli “buuune (!!!)”. Exemplul 1) Profesori care din prima sau cel târziu din a doua problemă trec la calcul în iraţional, bulversând prin această mişcare toţi elevii care încă nu au înţeles aceste numere. Am întâlnit foarte multe astfel de cazuri; aş putea să spun că majoritatea colegilor din Cluj procedează în acest fel. Exemplul 2) Profesori care nu face probleme de calcul a ariilor la clasă pentru că acestea “sunt prea simple”, dar le cer apoi la teză. Am întâlnit chiar şi profesor care nu a predat teorema lui Pitagora deloc, dar la un moment dat au început să apară aplicaţii din senin (de obicei întâlneam acest obicei la clasa a 8-a, unde diferiţi profesori nu predau ariile şi volumele corpurilor, dar la un moment dat încep să le ceară la teste, după principiul minunat că “le găsiţi peste tot în cărţi”). Exemplul 3) După introducerea ciudată a teoremei lui Pitagora în finalul clasei a 6-a, te-ai fi aşteptat ca în clasa a 7-a, la lecţia despre arii să pornească şi folosirea teoremei lui Pitagora. Dar, nici vorbă! Mulţi profesori predau lecţia despre arii din semestrul I în continuare ca în anii precedenţi (dinaintea programei din 2017), teorema lui Pitagora apărând în probleme de-abia în semestrul al II-lea, aşa cum o făceau ei “de-o viaţă”. Astfel profesorii ratează ocazia de a ridica embargoul asupra planimetriei, singura formă clară de înţelegere a unor elemente de geometrie de către majoritatea elevilor, prelungindu-le de fapt “agonia teoreticistă” până spre primăvara clasei a 7-a.

Am uneori impresia că majoritatea profesorilor, atât cei de la clasă, cât şi cei decidenţi la nivel naţional, se preocupă doar în folosul vârfurilor, a celor maxim 10% din populaţia şcolară, abandonându-i, chiar împingându-i pe cei mulţi în mocirla necunoaşterii, a înjosirilor şi a frustrărilor, totul în numele unui olimpism exagerat, avându-şi originea în comunismul întunecat al lui Ceauşescu.

Cum parcurg eu acest drum? Am prezentat prin programa pentagonia în postări din vara lui 2019 cum încerc eu să vin în întâmpinarea elevilor de nivel mediu, care reprezintă însă marea masă a populaţiei şcolare (mai nou le spun simplu cei 80%). Iată, pe scurt, forma de predare practicată de peste 20 de ani, formă care le dă şi elevilor obişnuiţi şansa de a face “niţică geometrie”.

1) Prima parte o reprezintă înţelegerea rădăcinii pătrate, cel puţin la nivel aritmetic (adică calculul radicalilor în situaţii exacte, din numere pătrate, cât şi în situaţii aproximative, în cazul numerelor ce nu sunt pătrate); Desigur că aici se poate parcurge şi forma algebrică, adică exprimarea radicalilor din numere nepătrate prin scoaterea parţială a factorilor de sub radical (părerea mea este că această parte ar trebui să vină mai târziu, dar acesta este un alt subiect).

2) A doua parte o reprezintă calculul de arii, deducerea formulelor pentru triunghiuri şi patrulatere, cât şi scurte aplicaţii ale acestora. Aici fac şi partea de arii ce implică compararea acestora: figuri echivalente (de exemplu proprietatea de arie a medianei) sau alte aplicaţii.

3) A treia parte o reprezintă teorema lui Pitagora, justificată prin intermediul ariilor, pe baza căreia putem combina primele două părţi în probleme de calcul, adică de planimetrie. Concret, odată făcută şi teorema lui Pitagora, se pot da cât mai multe probleme de calcul a ariilor şi a perimetrelor, cu aflarea diferitelor lungimi necesare prin această cea mai importantă teoremă a geometriei gimnaziale. Aici fac multe aplicaţii cu rezultate întregi (triplete pitagorice), dar şi calcule de arii aproximative în cazuri de radicali din numere nepătrate (mai ales la diagonala în pătrat şi la triunghiul echilateral).

Acest parcurs al lecţiilor le dă elevilor obişnuiţi şansa să se exerseze pe probleme de calcul cu mai mulţi paşi logici, începând chiar din toamna clasei a 7-a. Această abordare permite umplerea clasei a 7-a cu probleme de planimetrie accesibile majorităţii elevilor. Rezolv astfel una din marile probleme ale geometriei gimnaziale actuale, anume că marea majoritate a elevilor pot găsi cu sens preocupările “aritmetice” planimetrie, dar nu înţeleg rostul demonstraţiilor şi logica acestora, astfel încât învăţarea lor se rezumă la învăţarea pe de rost a unor lucruri neînţelese. Aceşti copii vor învăţa prin repetiţie paşi de calcul cu teorema lui Pitagora şi aplicarea lungimilor în formulele de arie, astfel încât vor putea face matematică până la un nivel mulţumitor fără a înţelege demonstraţiile.

Ca o paranteză (în “războiul” meu cu stilul de matematică din America, stil numai bun de tâmpit copiii), trebuie să precizez că eu nu sunt adeptul unor formule pentru perimetre de învăţat pe de rost de către elevi. Perimetrul reprezintă un fenomen accesibil oricărui elev, iar aceştia vor trebui să “îşi deducă” în minte cum se calculează perimetrul unei figuri, mai presus de enumerarea şi însumarea tălâmbă a tuturor laturilor. Ce treabă am eu cu predarea din America? Păi, mă întâlnesc cu formule de perimetre în trusele geometrice făcute în China în principal pentru piaţa americană.

Ulterior, evident către primăvară, în urma lecţiilor despre asemănarea triunghiurilor din semestrul al II-lea, parcurgem şi demonstraţia teoremei lui Pitagora pe baza teoremei catetei (dată de Euclid). La această reluare pun accentul mai mult pe partea de iraţionalitate a calculelor şi a rezultatelor (după parcurgerea formulelor de calcul prescurtat se pot face şi alte demonstraţii ale teoremei lui Pitagora pe baza acestora). Acest pas este adresat elevilor buni la matematică, dar şi celor de nivel mediu care au parcurs şi au înţelesmulte elemente de geometrie prin intermediul problemelor elementare de calcul parcurse în semestrul I. Constantin Titus Grigorovici

P.S. După cum am spus, mi-am propus să anexez prezentului eseu, o scurtă descriere despre cum ar trebui parcursă introducerea, mai exact deducerea formulelor de calcul a ariilor în clasa a 7-a. Punctul de plecare raţional este reconectarea cu lecţia din finalul clasei a 5-a, chiar reluarea pe scurt a ideilor respective. Concret, există două tipuri de formule de calcul a ariilor: 1) formulele bazate pe principiile logice de bază, anume dreptunghiul şi pătratul (pătratul cu dublu rol, mai întâi ca unitate de măsură cea mai practică, apoi după dreptunghi, ca un caz particular al acestuia); 2) formulele ce pot fi deduse din primele pe baza unor raţionamente elementare, aici apărând – după părerea mea – ariile pentu majoritatea figurilor în următoarea ordine: triunghiul dreptunghic, paralelogramul, triunghiul oarecare, rombul şi trapezul. Daţi-mi voie să le prezint pe rând, în ordinea cea mai naturală gândirii şi deducţiei logice (o minunată ocazie de predare prin problematizare, adică prin întrebări). Voi enumera fiecare situaţie şi voi descrie raţionamentul pe care se poate gândi, fără să mai fac şi figurile (dar cu elevii figurile devin partea de bază; cu ei nu scriem decât formula în urma dialogului şi a explicaţiilor orale; cu elevii totul devine cât mai vizual posibil).

Triunghiul dreptunghic: aria sa este jumătate din aria dreptunghiului, lungimea şi lăţimea devenind aici cele două catete (desenul conţine un triunghi dreptunghic cu o catetă orizontală şi una verticală, completat cu linie punctată la un dreptunghi, faţă de care aria triunghiului este jumătate, adică “supra 2”).

Paralelogramul: se reduce la formula dreptunghiului dacă trasăm o înăţime, decupăm triunghiul dreptunghic format şi “îl lipim” în capătul celălalt al paralelogramului.

Triunghiul oarecare: este jumătate dintr-un paralelogram (deci, doar aici apare posibilitatea justificării raţionale a formulei de arie a triunghiului oarecare!!!)

Rombul: pus “ca un diamant”, rombul poate fi încadrat într-un dreptunghi (desenat cu linie întreruptă) cu laturile paralele cu diagonalele rombului. La numărarea triunghiuleţelor se vede că rombul are aria cât jumătate din aria dreptunghiului

Trapezul: aici există cel puţin 2-3 variante de deducere a formulei (1- completarea trapezului cu încă unul la fel, dar cu capul în jos, alături, astfel încât să formeze împreună un paralelogram cu baza egală cu suma bazelor trapezului; 2- trasarea liniei mijlocii MN şi a înălţimilor prin M şi N, după care două triunghiuri dreptunghice diferite de la baza mare se rabatează în sus, la baza mică, transformând trapezul într-un dreptunghi cu lungimea cât linia mijlocie etc.)

Pătratul (2): trasând un pătrat care stă cu diagonalele verticală, respectiv orizontală se poate adapta aria de mai sus a rombului.

Rombul (2): Construind un romb culcat, adică în formatul “paralelogramic”, se poate adapta acestuia formula de la paralelogram. Ca “spirit” al rombului este însă evident că aceasta este a doua formulă pentru aria rombului, în nici un caz prima.

Aici mai are sens a fi discutată doar ideea că la triunghiul isoscel, cât şi la triunghiul dreptunghic cu baza pe ipotenuză, se aplică tot aria triunghiului oarecare. Este evident că aria triunghiului echilateral, formula lui Heron cât şi aria cercului nu-şi au locul aici. Ele ar trebui să apară mai târziu dar, din păcate, mulţi profesori le dau aici, deşi acestea nu pot fi justificate în nici un fel în această fază de gândire (acesta este alt subiect, la care îmi doresc să revin cu altă ocazie).

Clasa a 6-a nu se ocupă mai deloc de subiectul planimetriei sau al stereometriei în sensul prezenţei calculelor de arii sau volume. În afara unor apariţii sporadice şi întâmplătoare în probleme de aritmetică, doar lungimea apare uneori, eventual perimetrul unui triunghi. Întreaga clasă a 6-a se ocupă la geometrie doar de studiul proprietăţilor şi de demonstrarea acestora. Se încalcă astfel un principiu psiho-pedagocic de accesibilitate faţă de vârsta copiilor, conform căruia elevii de clasa a 6-a nu sunt încă pregătiţi pentru o abordare euclidiană a geometriei, dar ar putea înţelege elemente de măsurare şi calcul pe figurile geometrice studiate, cât şi activităţi de construire a diverselor situaţii. Abordarea geometriei de clasa a 6-a se situează pe partea greşită a axelor descrise în prima parte a acestui eseu, atât din punct de vedere a axei pedagogie-ştiinţă, cât şi din punct de vedere a axei calcule-demonstraţii.

Avem aici o mare problemă: marea majoritate a elevilor pot găsi cu sens preocupările “aritmetice” ale planimetriei, în sensul calculării perimetrului sau a ariei unei figuri (cu implicaţii practice de tipul determinării lungimii plintei şi a suprafeţei unei camere în care trebuie pus parchet). Dimpotrivă, studiul demonstrativ abstract al figurilor geometrice este mult mai puţin accesibil majorităţii elevilor. Chiar începând chiar de la introducerea acestei abordări prin manualele din 1981, cel mult 2-3 elevi din clase înţelegeau ce se întâmplă la geometrie în clasa a 6-a. Pe cale de consecinţă, pentru marea majoritate a elevilor, geometria de clasa a 6-a reprezintă o materie de neînţeles, la care trebuie tocite atât teoria cât şi “problemele”, pentru că elevii nu le văd un sens practic.

Dar nu doar că marea majoritate a elevilor primesc o materie e care de fapt nu o înţeleg şi căreia nu-i văd sensul, dar ei nu parcurg o materie practică cu aplicabilitate în lumea din afara matematicii. Vreau să atenţionez aici o diferenţă majoră între geometria teoretică cu demonstraţii (o materie orientată egocentrist, autosuficient, înspre propriile nevoi de dezvoltare) şi geometria planimetrică, asociată şi cu geometria construcţiilor practice a figurilor, care este o materie aplicativă (o materie orientată altruist, în folosul aplicaţiilor extramatematice). Majoritatea elevilor nu pot să intre cu adevărat în lumea închisă a matematicii, dar – în urma unor incursiuni cu sens la orele de matematică – ar putea dobândi arta aplicării cunoştinţelor matematice în situaţii practice. Parcurgerea unei materii egocentriste în şcoală, fără aplicabilitate direct, reprezintă una dintre cauzele majore a situaţiei dramatice constatată la nivel naţional prin studiile PISA.

Există şi alte surse de atenţionare a faptului că material nu este bine astructurată. O aranjare teoreticistă, care neglijează nevoile practice ale omului de rând, cât şi nivelul maxim de aplicabilitate matematică al celei mai mari părţi a populaţiei, duce la o reală pierdere de vreme în şcoală pentru majoritatea populaţiei şcolare. Părerea mea este că foarte mulţi elevi vin degeaba la orele de matematică în clasa a 6-a (dar şi în alte clase), pentru că material parcursă nu li se adresează defel! Fenomenul se accentuează până al aproape general în cazul şcolilor de la sate, fapt subliniat şi în ultimul raport World Vision pentru România.

Dar lucrurile stau prost nu numai la sate. Şi la oraşe există o mare parte a populaţiei care nu se allege cu nimic din orele de matematică. Să vă dau un exemplu văzut din întâmplare în aceste zile. Mă uitam la o emisiune despre un American pasionat de maşini, care recondiţiona împreună cu angajaţii săi maşini vechi. În exemplul concret găsiseră o maşină “tare” de la sfârşitul anilor ’60, pe care o analizau cu mult entuziasm. Ajungând la ţevile de eşapament, au comentat că acestea ieşirile originale dreptunghiulare (în comentariul englezesc a fost folosit cuvântul “rectangle”). Ei bine, traducătorul subtitrării în română a folosit cuvântul “pătrate”, deşi se vedea clar că ieşirile au formă dreptunghiulară. Dar, ce-l interesează astfel de detalii pe un absolvent de filologie? Pentru acel traducător, chiar şi dreptunghiul reprezintă o figură prea neobişnuită, care-i crează repulsie din vremea când se chinuia să supravieţuiască cumva orelor de matematică.

Practic, revenind la subiectul nostrum, destul de repede după introducerea ariei şi a volumului ca fenomene de măsurare la sfârşitul clasei a 5-a, apare un embargou în folosirea acestora, embargou ce durează practic de la începutul clasei a 6-a, până la studierea completă prin demonstraţii a figurilor de bază, a triunghiurilor şi a patrulaterelor. De abia după studierea teoretică a acestora (adică după un an şi un sfert) se revine la planimetrie, adică prin toamna clasei a 7-a.

Dar şi atunci, abordarea este foarte rară la nivelul accesibil majorităţii, pentru că – nu-i aşa? – noi, profesorii, nu ne pierdem vremea cu “prostii”! În plus, apare şi o interferare brutal dinspre o ordonare la fel de agresivă din partea algebrică a programei, anume a parcurgerii practice simultane a rădăcinii pătrate aritmetice (cu rezultate întregi sau aproximative) cu forma algebrică a radicalilor (cu rezultate exacte, dar iraţionale). Elevii buni fac faţă acestei abordări, dar larga majoritate clachează total sau, eventual se refugiază în învăţarea pe de rost. Parcurgând din start aplicaţii iraţionale (pentru “cei buni” desigur), profesorimea închide “poarta înţelegerii” geometriei pentru foarte mulţi elevi.

Embargoul asupra stereometriei este dublu, adică de doi ani şi jumătate, neglijând cu totul necesitatea formării şi antrenării vederii în spaţiu prin intermediul desenării corpurilor geometrice şi a forţării minţii elevului de a-şi imagina aceste desene plane drept corpuri 3D (din pedagogia Waldorf am aflat că vederea în spaţiu sănătoasă trebuie să se fi format până la vârsta de 13-14 ani, altfel se închide “fereastra temporală” de formare a vederii sănătoase tridimensionale; ne mirăm apoi că elevii de liceu, sau mai târziu adulţii, nu înţeleg diferite situaţii de ordonare spaţială, mai ales că în liceu oricum acestea nu se mai reiau, ca pe vremuri).

Din nou, am impresia că are loc aici o “conspiraţie” generală şi bine pusă la punct împotriva elevilor de rând, cei care reprezintă majoritatea covârşitoare a populaţiei şcolare. Singurii care pot trage foloase din această formă actuală de geometrie sunt cei 2-3 potenţiali olimpici, care au oricum şi acasă profesor particular şi după care se reglează întreaga predare a profesorului de la tablă. În rest, toţi ceilalţi elevi sunt supuşi constant unei înjosiri prin neînţelegere, proces cu urmări de neînchipuit la nivel psihic. Rezultatul este că toţi elevii (ai căror părinţi “pot”) sunt forţaţi “să-şi ia profesor” pentru a face faţă situaţiei. Am întâlnit chiar un caz de şcoală particulară, deci cu taxe serioase, la care în clasa a 6-a toţi elevii erau nevoiţi să aibă în paralel şi profesor în particular, pentru a face faţă predării şi cerinţelor profesorului de matematică, măcar la un nivel de promovare a clasei.

Precizez că mă refer aici la elevul de rând, atât cel care oricum are dificultăţi în a înţelege ce tot vor “ăştia din jurul lui” cu atâtea demonstraţii, dar şi la cel cu note destul de bune la matematică, dar neolimpic. Toţi aceştia nu înţeleg mare lucru din materia de clasa a 6-a, aşa că învaţă pe de rost atât teoria, cât şi problemele. Implicându-mă în căutarea unor soluţii de corectare a situaţiei, respectiv de găsire a unor căi în sprijinul învăţării geometriei de către toţi ceilalţi elevi în afară de vârfurile clasei, eu încerc să mai fac paşi în sprijinul majorităţii elevilor. În primul rând, încerc să accesibilizez geometria din timpul embargoului asupra planimetriei, punând un accent mai puternic pe construcţiile practice ale figurilor geometrice (cu folosirea tuturor instrumentelor geometrice), şi folosind din planimetrie măcar măsurările şi construcţiile concrete de laturi şi de unghiuri (aici merg desigur şi perimetrele). În afară de asta mă străduiesc să le dau elevilor noţiunile cât mai intuitive posibil, pentru a le accesibiliza cât mai bine material. Predarea prin problematizare ajută desigur mult în parcurgerea materiei. Nici eu nu ştiu cum aş putea elimina cu totul această perioadă de introducere a tuturor noţiunilor teoretice ale geometriei, dar încerc să o fac cât mai scurt şi cât mai accesibil elevilor de rând.

Legat de scurtarea acestui embargo asupra planimetriei, eu încerc să mă rezum doar la nivelului clasei a 6-a. Cu alte cuvinte, încerc să şi reduc perioada lipsită de calcule de arii doar la un an, nu la 1,5 ani. Concret, eu încerc la fiecare clasă a 6-a să parcurg în final, în acelaşi mod intuitiv şi capitolul despre studiul patrulaterelor (fără aplicaţii, cum ar fi de pildă linia mijlocie). Nu este nimic aberant în acest gest: până la sfârşitul anilor ’90 patrulaterele erau încă în clasa a 6-a. Eu mi-am dat inspecţia de gradul II, în primăvară la o clasă a 6-a, cu lecţia despre linia mijlocie în trapez. Avem şi o dovadă clară în acest sens, cunoscută tuturor: manualele alternative din 1997 au fost redactate după o programă conţinând patrulaterele în clasa a 6-a, iar altele nu au mai fost aprobate, aşa încât până în urmă cu doi ani, adică până la manualele actuale conform programei din 2017, manualele de clasele 6 şi 7 erau retipărite cu patrulaterele în clasa a 6-a, nu în a 7-a.

La ce mă ajută parcurgerea intuitivă, superficial-observaţionistă a patrulaterelor în finalul clasei a 6-a? Mă ajută atât în direcţia elevilor buni, cât şi în direcţia celor mediocri sau slabi. Eliberând presiunea asupra începutului clasei a 7-a, în primul rând eliberez un spaţiu temporal în care pot parcurge pentru elevii buni un spectru mai larg de demonstraţii geometrice, nu doar prin congruenţa triunghiurilor, ci printr-o diversitate mai largă de demonstraţii.

Cât despre ceilalţi elevi, cei mediocri dar mulţi, acestora le ofer posibilitatea ca destul de repede în clasa a 7-a să pornească cu calculele specifice teoremei lui Pitagora, ajungând în sfârşit să facă şi ei geometria căreia îi văd sensul, anume planimetria. Dar despre acest subiect vom discuta pendelete în următoarea parte a eseului de faţă. Constantin Titus Grigorovici

P.S.  Vorbeam mai sus de toţi elevii care nu înţeleg mare lucru din materia de clasa a 6-a, aşa că învaţă pe de rost atât teoria, cât şi problemele (cei care cât de cât se preocupă, dar şi cei ai căror părinţi îi forţează spre rezultate la şcoală, că despre cei mulţi de la sate oricum nu se prea vorbeşte decât separat).

Teoria trebuie să o înveţe pe de rost pentru că li se cere la lucrări de control să redea diferite definiţii. Şi aici găsim – apropos – acea formă de bullying, de răutate teoretică de care am vorbit în în partea a doua a acestui eseu, elevii simţindu-se agresaţi constant de către profesorul de matematică. La exemplul şcolii de mai sus, elevii de clasa a 6-a primiseră să redea în diverse teste, de trei ori la rând, următoarea definiţie “Două drepte coplanare neintersectate se numesc drepte paralele”. Elevii nu înţelegeau despre ce este vorba, pentru că ei făceau geometrie doar în plan şi – pur şi simplu – cuvântul “coplanare” nu le putea intra în minte, producând blocaje în cascadă. Imediat ce scoteam acest cuvânt din definiţie, lucrurile se luminau şi totul era în ordine. Pentru elevul de rând (99,99% din populaţia şcolară) poţi vorbi cu sens despre anumite puncte din plan, doar atunci când ai trecut la geometria în spaţiu. Cuvântul “coplanar” face parte din vocabularul clasei a 8-a şi nu are ce căuta la clase mai mici în ora de matematică! Folosirea acestuia în clasa a 6-a reprezintă o dovadă clară de bullying intelectual din partea profesorilor la adresa elevilor.

Acest bullying a pornit însă official de mult, odată cu manualele de clasa a 6-a de la începutul anilor ’80, când se vorbea despre “punctele din plan” şi a început să se introducă noţiunea de “semiplan” pentru a se putea define riguros ce-i acela interiorul unui unghi (intersecţia dintre semiplanul determinat de dreapta suport a unei laturi a unghiului ce include cealaltă latură, cu semiplanul determinat de dreapta suport a celei de-a doua laturi ce include prima latură – cam aşa ceva era, mă scuzaţi că nu fug acum să caut un astfel de manual ca să dau această definiţie cu citat şi sursă). Noţiunea de interior al unghiului devenea astfel ceva de neînţeles, trăgând în groapa neînţelegerii şi definiţii ulterioare stupide, cum ar fi definiţia bisectoarei (o semidreaptă cu originea în vârful unghiului, ca formează cu laturile unghiului două unghiuri congruente). Dar ambiţia de a introduce interiorul unghiului pe bază de semiplane, conform teoriei mulţimilor, a dus şi la alte tâmpenii, cea mai mare fiind eliminarea din material şcolară a unghiurilor cu o descidere mai mare de 180^o (unghiuri supraobtuze), deci desigur şi a unui studiu minimal al patrulaterelor concave. Lucrurile au mers mai departe în cascadă: dacă elevul a reuşit cumva să înţeleagă ce înseamnă acela un “triunghi oarecare”, la patrulatere nu are voie să folosească noţiunea similar de “patrulater oarecare”, pentru că sunt interzise cele concave. Denumirea de “patrulater convex” este mult prea pretenţios-teoreticistă, făcând noi victim în strădania de înţelegere a demonstraţiei de către elevi.

Dar şi problemele de geometrie din clasa a 6-a sunt învăţate pe de rost, pentru că elevii nu le văd sensul. Ce au făcut în această situaţie diriguitorii matematicii şcolare româneşti? În urmă cu peste 20 de ani au scos patrulaterele din clasa a 6-a, mutându-le la începutul clasei a 7-a şi prelungind astfel embargoul de care am vorbit mai sus la adresa unei matematici mai accesibile elevului de rând. Dar şi în cadrul demonstraţiilor din semestrul al II-lea al clasei a 6-a, profesorii se concentrează mai ales pe “cele mai importante”, adică pe demonstraţiile prin metoda triunghiurilor congruente. Absolutizarea acestei metode, care este una destul de abstract pentru mintea de începător a elevului de a 6-a, această absolutizare duce la toceală, elevii ajungând să simtă nevoia a o învăţa pe de rost.

De pildă, dacă dai unui elev obişnuit la începutul clasei a 7-a o problemă cu unghiuri, el ţi-o va “rezolva” oricum cu metoda triunghiurilor congruente (că merge, că nu merge), arătându-ţi de fapt că el nu a înţeles nimic din demonstraţiile clasei a 6-a. Preferata mea în acest sens este următoarea problemă (ca să vă lămuresc ce vreau să spun): Considerăm triunghiul oarecare ABC în care bisectoarea unghiului B taie latura opusă în D şi trasăm prin D paralela DE BC, E  [AB]. Demonstraţi că [BE]  [ED]. Păi, să vedeţi câte demonstraţii cu congruenţa triunghiurilor am văzut dea lungul anilor la această problemă! Te doare capul!

Din păcate, o astfel de abordare a materiei, o învăţare pe de rost atât a teoriei, cât şi a problemelor, ani de-a rândul, chiar decenii întregi, nu are cum să nu lase urme de nedorit în gândirea logică a poporului, chiar şi a celor ce se pretend culţi. Oamenii ajung să evolueze şi să studieze orice într-un mod total paralel cu matematica (adică neatingându-se cu adevărat cu gândirea din matematică), eludând matematica şi rămânând fără o gândire logică în adevăratul sens al cuvântului. Mulţi români “mimează” gândirea şi argumentaţia logică, pentru că de fapt nu au participat cu sufletul şi cu mintea la orele singurei materii care le putea forma gândirea cauzală, ei mulţumindu-se să înveţe elementele lecţiilor pe de rost (să nu-mi spuneţi despre material numită “logică” din liceu, pentru că aceasta cu greu poate fi înţeleasă că ar putea educa la elevi o gândire logică). Dar nu foştii elevi sunt de vină pentru această evoluţie total paralelă cu matematica, ci mai degrabă abordarea îngâmfată a matematicii (atât din punct de vedere a programei, cât şi a profesorilor), care se prezintă exclusivist şi repulsiv în faţa marii majorităţi a elevilor. Există prea multe exemple în acest sens, dar prefer să nu intru într-o astfel de discuţie, aşa că mă opresc aici.

În prima parte a acestui eseu am luat în discuţie planimetria şi sterometria, dar am încercat şi să pregătesc contextul mai larg legat de problema diferenţelor majore între domeniul acestora şi domeniul demonstraţiei geometrice. Să reluăm pentru început ce-i cu aceste denumiri ciudate, rar folosite în România.

Planimetria se referă la toate acele componente ce se referă la măsurarea (în general metric) a figurilor geometrice plane. Concret, este vorba de determinarea lungimilor în vederea calculului de perimetre şi arii (2D). Stereometria, în mod similar, se referă la măsurarea spaţiului, adică la determinarea ariilor şi volumelor diferitelor corpuri geometrice (3D).

Atât planimetria cât şi sterometria apar clar începând de la sfârşitul clasei a 5-a, prin unităţile de măsură corespunzătoare, motorul preocupaţional reprezentându-l aplicaţiile la fracţiile zecimale. În acest moment se simte clar cât este de greu a porni o nouă materie, dacă ai pretenţia de a preda cât de cât riguros. La unităţile pentru arie trebuie să te bazezi pe faptul că elevii ştiu din clasele mici ce-i acela un pătrat, dar acesta nu a fost predate riguros axiomatic, ci a fost cunoscut doar în mod intuitiv (nu intru aici în procesul prin care un copil poate înţelege ce-i acela un pătrat sau un dreptunghi, dar strădania din clasa a 5-a în noile manual nu este deosebit de reuşită)). La cub lucrurile stau similar, cu diferenţa că spre deosebire de pătrat ce poate fi schiţat, desenat intuitiv, cubul este mult mai greu de prezentat în desen de către copil.

Astfel, este absolut normal ca preocuparea principală să cadă pe arii, volumul fiind abordat intuitiv, în mod similar cu aria (mutatul virgulei în sistem zecimal), şi căutată cât de repede conexiunea cu capacitatea (legăturile dintre litraj şi cubaj). Figura de bază la arie o reprezintă dreptunghiul şi, în mod similar, corpul de bază la volum îl reprezintă paralelipipedul dreptunghic. Pătratul apare la arii în două poziţii diferite, la început ca unitate de măsură, iar apoi din nou ca un caz particular de dreptunghi. Repet şi precizez: principiul de bază pentru formulele de arie îl reprezintă dreptunghiul (de exemplu, eu consider de fiecare dată un hol la care se pun patru rânduri de câte şapte plăci de gresie, deci sunt necesare cu totul  de plăci); formula de arie a pătratului reprezintă doar un caz particular al celei a dreptunghiului. Lumea profesorilor nu este cu adevărat conştientă de această duplicitate a pătratului (se vede acest fapt din felul cum se predă fizic sau în cărţi). Acelaşi fenomen îl întâlnim şi la volum, în “jocul” dintre cub şi paralelipipedul dreptunghic.

Înainte de a merge mai departe în eseul despre importanţa planimetriei şi a stereometriei în şcoli, îmi permit să mai zăbovesc puţin “pe aici”, fiind prea aproape de câteva idei metodico-didactice, încât să îmi permit să le ratez.

*

Legat de momentul introducerii ariei şi a volumului, respectiv a analogiei dintre modul de a gândi în cele două situaţii, în primul rând ar fi de atenţionat asupra faptului că amândouă măsoară mărimea interiorului, aria = interiorul unei figure plane (adică în 2D), pe când volumul = interiorul unui corp în spaţiu (adică în 3D). Acest aspect a fost observat în urmă cu mulţi ani (mai exact în toamna lui 2003) de către un elev dintre cei mai slabi la matematică în clasa respectivă, care a ridicat brusc mâna în timpul orei despre cub în clasa a 8-a, în momentul când lămurisem formula pentru aria totală: dar aria aia dinăuntru când o facem? Nefiind un elev tare pasionat de matematică, acesta a uitat că în clasa a 5-a vorbisem deja de volum; fiind însă un om foarte practic, acesta a sesizat imediat că în spaţiu mai este ceva similar cu situaţia ariei din plan. Am cuprins această idee în următoarea lecţie de prezentare generală a celor trei cuvinte “de calculat” la clasa a 5-a , perimetru, arie şi volum.

Un al doilea aspect ce merită evidenţiat aici se referă la folosirea cuvintelor pătrat respectiv cub pentru puterile a doua şi a treia. Eu studiez cu elevii în semestrul I al clasei a 5-a numerele figurate pe bază de punctuleţe (în plan, respective cu biluţe în spaţiu) şi lămuresc acolo de unde vine denumirea de “trei la pătrat” pentru 3² (la început chiar folosesc o scriere de felul 3□ pentru numere pătrate, iar prin analogie 3Δ pentru numere triunghiulare). Dacă nu intraţi în acest subiect în semestrul I, în apropierea momentului când predaţi puterile, atunci este neapărat necesar de a puncta sursa acestor denumiri ciudate atunci când studiaţi în finalul clasei a 5-a aria pătratului, respectiv volumul cubului.

Pentru un al treilea aspect, ce merită aici evidenţiat, trebuie să vă pregătiţi de o nouă critică dură la adresa matematicii şcolare din România. Figurile de bază în planimetrie (2D) sunt pătratul şi dreptunghiul, denumirile acestora fiind amândouă uşor de folosit şi în afara matematicii (putem vorbi liniştit despre o masă pătrată sau un teren dreptunghiular etc.). Corpurile de bază în stereometrie (adică în spaţiu, deci în 3D) sunt cubul şi paralelipipedul dreptunghic. Sesizaţi problema?

Dacă ne este uşor să vorbim despre cubuleţe de zahăr (care de obicei nici nu prea sunt chiar cuburi), ne va fi greu să vorbim despre o cutie paralelipiped-dreptunghică!!! Uau! Cei aia? Aici, în strădania de a găsi un echilibru între corectitudinea teoretică şi o exprimare cât de cât folosibilă din punct de vedere practic, mulţi vorbesc despre o cutie paralelipipedică. Este clar însă că această exprimare este greşită, chiar şi numai dacă ne gândim că, făcând drumul analogiei invers, ar trebui să vorbim despre o masă paralelogramică!!! Şi în geometrie poate fi făcută această analogie: astfel, în geometria plană ar trebui să vorbim despre un paralelogram dreptunghic!!!, nu despre un dreptunghi (la fel cum vorbim despre un triunghi dreptunghic sau despre un trapez dreptunghic). Făcând din nou drumul analogiei de la 2D la 3D, de vreme ce vorbim de un teren dreptunghiular, ar trebui să putem vorbi de o cutie dreptunghipedică!!!

Simţim aici că suntem împinşi într-o situaţie de blocaj: matematicienii folosesc pentru corpul care este cel mai des întâlnit la ora actuală o denumire total nefolosibilă din punct de vedere practic, forţându-ne la exprimări incorecte de tipul: 99,99% din tot ce se ambalează vine ambalat într-o cutie “dreptunghiulară”. Eu am sesizat acest aspect pentru că în limba germană cunosc o denumire mult mai lesne de folosit. Astfel, nemţii au în 2D denumirile Quadrat (pătrat) şi Rechteck (dreptunghi), iar în 3D denumirile Würfel (pentru cub), respectiv Quader (pentru paralelipipedul dreptunghic). Este evident că denumirea nemţească este mai uşor de folosit şi în situaţii practice, în afara matematicii, fiind mult mai scurtă decât cea prezentată în şcolile româneşti.

Pentru cei care vor susţine că asta e, n-ai ce-i face, rigurozitatea în matematică primează, acestora le-aş răspunde că există aici şi o clară doză de răutate, un soi de “bullying ştiinţific”. Cum îmi susţin un astfel de punct de vedere? Păi, fenomenul continuă prin seturile de probleme, din manuale sau culegeri, dar şi în prin alte exemple. Apar tot mai des exprimări de felul: “o prismă dreaptă cu baza pătrat” în loc de oficiala “o prismă patrulateră regulată”, sau “o piramidă triunghiulară regulată cu muchia laterală egală cu muchia bazei” în loc de “tetraedrul regulat”. Una din cele mai mari răutăţi întâlnite în ultimii ani a fost expresia “cubul PIRAMIDĂ”.

Dar să ne rezumăm doar la exemplul cu prisma dreaptă. Pentru ca elevii să înţeleagă ce-i aia o prismă dreaptă, ar trebui să le explicăm cum este o prismă care nu e dreaptă, adică să le povestim de prisma oblică, dar şi să le dăm exemple de prismă dreaptă dar neregulată. Toate acestea sunt însă abuzuri la adresa elevului de rând, care este constant înjosit că nu ştie cutare sau cutare lucru. Aceste abuzuri ar trebui interzise de către organizatorii materiei de predate, de vreme ce profesorimea, prin redactorii de manual sau auxiliare, nu se poate stăpâni să nu facă tot timpul acest bullying ştiinţific la adresa elevilor de rând.

Revenind la exemple mai paşnice, am observant de-a lungul anilor că doar noi românii folosim “tetraedru regulat”, toată lumea folosind simplul “tetraedru” pentru corpul perfect regulat; tot felul de alte tetraedre nu se studiază în materia pentru oameni obişnuiţi în şcolile din vest (pentru situaţiile special, adică la studierea unor tetraedre care nu sunt regulate, mă gândesc că ei le descriu concret în situaţia respectivă).

Ce-i de făcut? O posibilitate ar fi reintroducerea obligatorie, atât prin programa naţională cât şi prin manualele oficiale, a unei vechi denumiri, anume cea de cuboid. Desigur că mulţi ar sări în sus “ca o bombă americană” la aşa o inepţie. S-a mai încercat acest lucru, dar destul de timid spre sfârşitul anilor ’90, pe vremea introducerii primului Examen de Capacitate, dar mişcarea a fost destul de firavă şi a murit în faşă. O variantă de compromis între cele două extreme (rigurozitatea teoretică şi accesibilitatea practică a denumirii) am găsit-o la străini: astfel, nemţii folosesc uneori în predare, când vorbesc despre cub, concomitent două denumiri sinonime “Würfel oder Cubus” (”zar sau cub”; cuvântul Würfel este folosit atât pentru cub cât şi pentru zar; nemţii folosesc mai rar şi denumirea Cubus preluată din cultura renascentistă care s-a desfăşurat iniţial preponderent în latină).

În acelaşi fel nemţii mai folosesc deseori două denumiri sinonime împreună şi când vorbesc despre congruenţă: astfel, de multe ori profesorii germani folosesc expresia dublată “congruent sau egal prin suprapunere” (în germană:”congruent oder deckungsgleich”). Ei folosesc dubla denumire la început, până când se asigură că auditoriul şi-a amintit de denumirea teoretică, după care le folosesc liniştit alternativ, când pe una, când pe cealaltă. La fel am putea preda şi noi despre “paralelipipedul dreptunghic sau cuboidul”. Dacă apoi am folosi în probleme alternativ cele două denumiri, când una când cealaltă, sau uneori împreună, am putea da drumul oficial şi folosirii în viaţa extra-matematică a unei denumiri mai practice, astfel aceasta fiind recunoscută drept corectă teoretic. Atenţionez că aici vorbesc oricum de un proces de lungă durată (10-20 ani).

Desigur că există şi o altă variantă, anume acea a inventării unui nou cuvânt pentru acest corp atât de răspândit în lumea actuală. De pildă, am putea introduce denumirea de “dreptunghioid”. Expresia “o cutie dreptunghioidă” nu ar fi cu nimic mai complicată decât expresia “o cutie paralelipipedică”. Se pot găsi însă şi alte denumiri, dar problema este ca să fie acceptată existenţa acestei gafe de proporţii între lumea matematică şi lumea de zi cu zi, cât şi să se caute soluţii de rezolvare din partea oficialităţilor.

Doresc însă să scot în evidenţă şi un alt aspect al acestei stupide situaţii, anume ruptura dură existentă în societatea românească între poporul de rând şi specialiştii dintr-un domeniu. Aceştia din urmă s-au obişnuit să-şi impună un limbaj de specialitate îngâmfat, “cu nasul pe sus”, forţând plebea la o stare de înjosire lingvistică prin care să se simtă incapabili. La rândul lor, oameni de rând învaţă din această stare de îngâmfare teoreticistă a specialiştilor doar să nu-i respecte, să nu-i creadă, creându-şi o lume separată a lor, la nivelul lor de incultură. Ne-am mirat apoi, în perioada din urmă, de ce mare parte a poporului român nu-i crede, nu-i înţelege şi nu-i ia în seamă pe specialişti, atunci când aceştia ne vorbesc despre pericolul reprezentat de Covid 19 şi “se dau de ceasul morţii” rugându-ne să păstrăm distanţarea fizică şi socială. Glumind şi parafrazându-l pe Cornel Udrea (efectul razelor de lună asupra galoşilor de gumă), am putea vorbi aici sub titlul “paralelipipedul dreptunghic şi pandemia de Coronavirus la români”. Constantin Titus Grigorovici

Geometria are două componente clar diferenţiate. Pe de o parte sunt elementele de măsurare şi calcul al diferitelor mărimi (de obicei lungimi şi determinarea unor perimetre, arii sau volume, dar uneori sunt implicate aici şi determinări de unghiuri). Calculele de perimetre şi arii ale figurilor plane sunt reunite în general sub denumirea de planimetrie, pe când calculele de arii şi volume ale corpurilor poartă denumirea generică de steriometrie. Pe de cealaltă parte sunt elementele de studiere a proprietăţilor diferitelor situaţii (figuri sau corpuri), proprietăţi ce trebuie dovedite prin demonstraţii. Celor două componente să le spunem pe scurt calcule geometrice şi demonstraţii geometrice. Aceste două vaste domenii de activitate a geometriei sunt destul de bine delimitate, deşi ele interferează în multe zone intens.

În prezentul eseu doresc să evidenţiez un anumit fenomen la care m-am referit de curând în “strigătul de indignare” http://pentagonia.ro/reforma-de-avarie-1/ despre “Reforma de avarie” declanşată în minister la sfârşitul lunii octombrie, când a devenit evident magnitudinea celui de-al doilea val al pandemiei. M-am mai referit la acest subiect şi într-un “strigăt de indignare” mai vechi, prin finalul lunii iunie 2020, în postarea de la adresa http://pentagonia.ro/en-2020-in-forma-de-avarie-si-excluderea-geometriei-aritmetice/ . Fenomenul despre care doresc să scriu a ajunns în cea mai dură actualitate pentru cei care “au ochi să să vadă”, dar pentru foarte mulţi acesta este încă invizibil. Din păcate însă, atunci când fenomenul va fi vizibil pentru toată lumea, va fi mult prea târziu, aşa cum se întâmplă de obicei în cazul majorităţii greşelilor educaţionale. De pildă, îmi şi imaginez cum “se vor cânta” toţi prin mass-media la următoarele teste PISA.

Pentru înţelegerea acestui fenomen este important ca cititorul să înţeleagă un câmp mai larg de aspecte ce influenţează predarea geometriei (pentru o lămurire cât mai bună rog cititorul să lectureze cu răbdare următoarele rânduri, acordându-mi creditul necesar, chiar dacă va părea o “teoria chibritului”, un “bla-bla”, un “bătut câmpii” fără un sens imediat)). Acest fenomen, despre care doresc să vorbesc, se află la concurenţa a trei axe de preocupare, ce trebuie lămurite în prealabil. Prima axă de preocupare este cea evidenţiată mai sus, anume axa de preocupare având într-o parte demonstraţia geometrică iar în cealaltă parte calculul diferitelor mărimi.

În studiul nostru, o a doua axă de discuţii o reprezintă parcurgerea materiei de la geometria plană la geometria în spaţiu (de la 2D la 3D, dacă este să folosim limbajul cu care sunt obişnuiţi mulţi copii), ordine faţă de care nimeni nu are obiecţii: de când lumea şi pământul studiul geometriei a plecat de la geometria plană spre geometria în spaţiu, deşi dacă ne gândim puţin, vom conştientiza că oamenii s-au confruntat de la începuturi în egală măsură cu geometria plană cât şi cu cea în spaţiu. Totuşi, dacă ne-am propune să analizăm ceva mai profund, eu cred chiar că în realitate oamenii au început să conştientizeze geometria prin construcţii, adică în 3D, dar au realizat imediat că aceasta se bazează pe proprietăţi ale geometriei plane, pe care au studiat-o mai clar, fiind mai accesibilă.

Există însă şi un exemplu unde din motive practice cunoaşterea a avut loc sigur datorită unor situaţii în 2D: mă refer aici la nevoia de măsurare a terenurilor – de unde vine chiar denumirea geometriei – şi vorbesc aici despre situaţia cu care se confruntau oamenii în Egiptul antic, chiar de la începuturile culturii apărută în valea Nilului, înconjurată de deşert, anume de necesitatea trasării urgente a parcelelor ţăranilor pe terenurile de pe care tocmai se retrăseseră apele Nilului după inundaţiile anuale. Acel teren mocirlos trebuia repede şi eficient delimitat celor ce urmau să-l lucreze pentru ca aceştia să-l poată însămânţa şi să pornească germinaţia. De la acest process au preluat grecii denumirea de geo-metria.

O a treia axă de interes pentru subiectul nostru o reprezintă axa ce uneşte cele două extreme preocupaţinale ale matematicii: predarea matematicii în şcoli şi matematica ca ştiinţă riguroasă (chiar prima ştiinţă ce s-a confruntat cu necesitatea unei rigurozităţi extreme). Este “la mintea cocoşului” că ordinea în care aceste două domenii pot apărea în viaţa unui om este cea prezentată aici: întâi îi este predată matematica elevului şi doar ulterior acesta, fostul elev, poate eventual ajunge ca matematician să practice ştiinţa matematică. Doar că “Nea Euclid”, în strădania sa de a organiza cât mai bine predarea, le-a cam amestecat cele două părţi. Restul “amestecăturii” şi inversarea ordinii naturale a acestor două etape l-au făcut ulterior urmaşii lui Euclid, acest proces de inversare a ordinii ajungând în secolul XX la un nivel obsesiv.

Astfel, pe de o parte avem impulsul natural din punct de vedere ştiinţific, anume strădania de ordonare teoretică riguroasă, pornind de la axiome şi construind pe baza definiţiilor şi a teoremelor toată geometria; acest sistem este cunoscut pe scurt ca sistem axiomatic sau euclidian, după numele celui care l-a introdus prima dată. Cel puţin în ultimele câteva secole toţi matematicienii s-au străduit să-l imite şi să-i perfecţioneze sistemul.

Pe de cealaltă parte avem necesitatea pedagogică naturală de a prezenta elevilor cunoştinţele într-o formă pe care aceştia să o şi înţeleagă, să le fie adusă în mod accesibil minţii lor de începători în ale geometriei. Aici există o sumedenie de reţete şi principii de abordare ce ne pot ghida în acest proces şi pot fi susţinute inclusiv din punct de vedere al psihologiei. Enumăr doar câteva: în primul rând ar fi predarea intuitivă, apoi predarea de la întreg la componente, la fel aş putea aminti predarea de la superficial la studiul profund, ce poate fi aplicată uneori în forma de predare în spirală, iar exemplele pot continua mult şi bine. În eseul de faţă mă voi referi la toate acestea atunci când voi vorbi de folosirea intuiţiei în predare, ca reprezentant al tuturor acestor mecanisme corecte din punct de vedere psihologic în procesul de cunoaştere a lumii.

Eu consider că marea dramă a predării matematicii în general, respectiv a geometriei în particular, o reprezintă obsesia matematicienilor din ultimul secol înspre direcţia unei ordonări axiomatic-ştiinţifice, dar din păcate automat în detrimental nevoilor psihologice ale elevului începător în studiul acestei materii (am scris foarte mult în ultimii cinci ani despre acest subiect, a fost una dintre preocupările mele de bază).

Concret, eu consider că intrarea în lumea geometriei se poate face doar prin zona intuitivă cu conexiuni practice, forma perfect ordonată din punct de vedere euclidian fiind potrivită doar ultimului nivel de cunoaştere a geometriei, anume cel ştiinţific. Predarea în şcoli a geometriei la nivelul primei treceri, adică la clasele gimnaziale, trebuie să respecte în primul rând principiile psihologice, cum ar fi intuiţia, şi doar dacă acestea sunt îndeplinite, putem să ne gândim ca predarea să capete şi anumite accente de ordonare euclidiană. O predare, adică o introducere a geometriei având în primul rând şi în mod obsesiv preocuparea de ordonare axiomatic-euclidiană (obsesie ce le-a fost impusă profesorilor din şcoli prin reforma uitată din 1980), o astfel de predare şi-ar avea loc doar la facultăţile de matematică, ca un exerciţiu de ordonare a introducerii cunoştinţelor; cel mult o astfel de formă de predare s-ar putea face eventual în clasele de liceu, însă la acest nivel doar cu anumite concesii în direcţia unei ordonări obsedate a rigurozităţii (ceea ce s-a şi întâmplat în manualele din 1978, dar aceste gânduri oricum nu mai sunt de actualitate din 1997 încoace, de când oricum nu se mai predă geometria sintetică în liceu).

Să rezumăm: pentru a înţelege fenomenul studiat, am propus un context format din trei axe de preocupare: 1) axa calcule – demonstraţii; 2) axa 2D – 3D; 3) axa pedagogie – ştiinţă. Ordinea dintre predarea cunoştinţelor legate de calcule şi a celor legate de demonstraţii poate fi analizată realist doar ţinând cont şi de celelalte două axe de discuţie. Altfel spus, ordinea justă a aranjării în materia şcolară a calculelor şi a demonstraţilor geometrice se poate face doar în contextul înţelegerii depline a celorlalte două direcţii preocupaţionale ale geometriei. În următoarele părţi ale acestui eseu voi face des trimiteri la argumente legate de confluenţa acestor trei axe. Constantin Titus Grigorovici