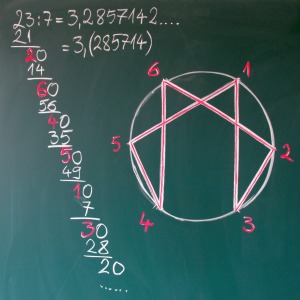Din start trebuie precizat că prezentul material reprezintă o creaţie personală 100%, găsit “din ȋntâmplare” într-un moment de inspiraţie, deşi am convingerea absolută că aspectele conţinute sigur au fost găsite şi de către alţii înaintea mea.
Dacă vom ȋmpărți la 7 un număr (nedivizibil cu 7) vom obține automat un rezultat ȋn forma unei fracții zecimale periodice. Asta cam știe toată lumea, dar este deja mai puțin evident că perioada acestor numere va fi ȋntotdeauna de exact 6 cifre (există și aici un studiu interesant ce se poate măcar porni cu elevii mai răsăriți: ȋmpărțirea la 3 sau la 9 are ȋntotdeauna perioada de o cifră; ȋmpărțirea la 11 are perioada de doua cifre; ȋmpărțirea la 37 are perioadă de trei cifre, pentru că 999 = 33·37; ȋmpărțirea la 7 are perioadă de șase cifre pentru că cel mai mic număr de forma 999…9 divizibil cu 7 este 999.999).
Până aici lucrurile se pot ȋnțelege relativ ușor de către o persoană doritoare de a aprofunda fenomenul (profesor sau elev). Oricum, pentru convingerea cititorului (acum), dar și a elevilor (la clasă), ȋn acest moment trebuie făcute câteva ȋmpărțiri (măcare vreo trei-patru, pentru a și vedea clar că ȋntotdeauna se obține o perioadă de șase cifre.
Analizând cu atenție perioadele acestor ȋmpărțiri vom vedea ȋnsă ȋncă ceva, mult mai surprinzător, anume că perioadele respective sunt ȋntotdeauna formate din următoarele cifrele: 1, 2, 4, 5, 7, 8. Numai acestea vor apărea ȋn perioada ȋmpărțirii la 7 și de fiecare dată apar toate șase, fiecare o singură dată.
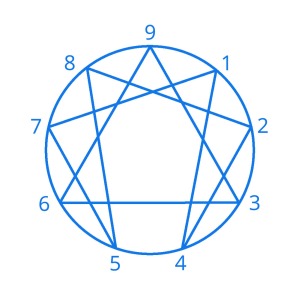
Mai mult, dacă ne uităm cu și mai mare atenție, vom vedea că acestea apar ȋntotdeauna ȋn aceeași ordine, una ciudată. De pildă vom putea ȋntâlni perioada 428571, sau perioada 571428, sau perioada 714285 etc. Cu alte cuvinte, ȋntr-o succesiune rotativă, după 7 vine ȋntotdeauna 1, iar apoi 4, urmat de 2 ș.a.m.d. Ȋncercând să reprezint grafic această succesiune pe cercul de 10 cifre, am obținut o structură ciudată care se repetă la nesfârșit, structură la care eu i-am spus “poarta ȋmpărțirii lui 7” sau mai pe scurt “poarta lui 7”. Atenționez asupra faptului că poarta va sta drept dacă vom ȋmpărți cercul cu cele zece cifre poziționate cu 9 și 0 sus echilibrate, respectiv 4 și 5 jos echilibrate, iar 2 și 7 la dreapta și la stânga.
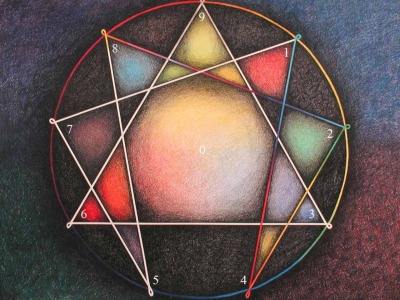
Ȋn momentul când am făcut prima dată o astfel de reprezentare grafică mi-am adus aminte că am mai văzut un astfel de desen pe un afiș lipit pe o clădire (cu cca. 20 ani în urmă), afiş ce invita la o prezentare cu context spiritual (la vremea respectivă nu am întreprins nimic în sensul cunoaşterii, respectiv a înţelegerii acestuia, nici din punct de vedere spiritual, nici din punct de vedere a logicii desenului). Mult mai recent, ulterior găsirii porții lui 7, am aflat că de fapt desenul respectiv este denumit eneagramă, că este de fapt o reprezentare pe un cerc cu doar nouă cifre (lipsind 0) și că acolo poarta lui 7 este completată cu un triunghi echilateral care unește multiplii rămași ai lui 3.
Revenind la poarta lui 7, dați-mi voie să vă mai arăt o surpriză a acesteia. Vă rog să luați ȋmpărțirile la 7 efectuate mai sus (sper că le-ați făcut cu mâna, nu pe calculatorul din deșteptofon; dacă nu – ghinion – tot trebuie să le faceți și pe hârtie) și analizați resturile intermediare ale scăderilor din timpul ȋmpărțirii (fiind vorba de ȋmpărțire la 7, resturile trebuie să fie de cel mult 6; pentru că nu are loc divizibilitatea, ȋmpărțirea nu se va termina, așa că nu vom avea restul 0). Astfel, veți vedea că resturile respective vor fi ȋntotdeauna toate cifrele de la 1 la 6, ȋntr-o succesiune ciudată, care se păstrează ȋnsă la toate ȋmpărțirile. Reprezentându-le pe acestea pe un cerc cu șase cifre (de la 1 la 6) vom avea surpriza să ȋntâlnim din nou poarta lui 7 (apare și reprezentată grafic pe cercul cu 10 sau 9 cifre, dar mai turtită și răsucită ȋntr-o parte; ȋn schimb arată destul de frumos și desenată pe un cerc cu șapte cifre, de la 0 la 6, cu 0 centrat sus).
Să analizăm puțin din punct de vedere metodico-didactic această ciudată “micro-lecție”. Este evident că produce uimire, deși nu este o lecție grea. Elevul exersează ȋmpărțirea și vede cum apare clar perioada. Ȋn plus, ȋși exersează atenția la detalii, face o reprezentare grafică (fiecare cât se pricepe de bine la trasarea cercului cu mâna și la ȋmpărțirea acestuia ȋn 10 sau 9, respectiv 6 sau 7 părți “egale”). Motivația pentru tot acest demers o reprezintă verificare prin obținerea acestui desen impresionant. Toți pașii sunt deosebit de accesibili. Ȋn final, orice elev are o satisfacție clară obținând respectivul desen misterios. Ȋn plus poate merge acasă să-i uimească cu acesta și pe părinți, care nu au ȋnvățat așa ceva ȋn școală. Desigur că nu are rost să-i alocăm acestei ciudate lecții tare mult timp; cred că două exemple cu reprezentările grafice corespunzătoare sunt suficiente (unul la tablă și unul ca muncă independentă ȋn clasă, plus ȋncă două la libera alegere ca temă). Și ca să fie clar, nefiind ȋn programă, nici nu cer astfel de exerciții la teste. Dar oricum, sunt sigur că elevii care le-au ȋnțeles se aleg cu câteva sinapse ȋn plus, ȋnvățând să conecteze un fenomen numeric cu o reprezentare grafică.
Părerea mea este că elevilor de clasa a 5-a le este suficientă această formă de lecție, fără o justificare sau cine știe ce demonstrație a ciudatului fenomen. La nivelul clasei a 5-a lucrurile pot rămâne ȋn această stare de uimire, de mirare pură. Dimpotrivă, la nivelul mai adult, de pildă ȋncepând din liceu, se poate cere și găsirea unei justificări raționale. Un astfel de studiu ar depăși ȋnsă cu mult nivelul de accesibilitate al clasei a 5-a. La acest nivel este arhisuficient atât, ȋncât să-i lăsăm pe copii ȋntr-o stare de uimire “magică”, plină de admirație față de “minunile matematicii”.
*
Cu elevii lucrez până aici. Pentru curiozitatea personală am căutat mai departe ca să ȋnțeleg, măcar la nivel superficial, care ar fi cauza pentru care poarta lui 7 este implicată ȋntr-un simbol spiritual, dar nu am găsit nimic, deși pare destul de evident că există o legătură (cred că orice ȋntâmplare este exclusă la un desen de această complexitate). Este ȋnsă la fel de evident că forma sa este deosebit de potrivită pentru a impresiona “adepții” unui curent spiritual, mai ales pe cei care nu ȋnțeleg “lucruri din-astea” și care se vor uita cu cea mai profundă admirație la “ȋnvățătorul” ce le folosește. Nu susțin la nivelul absolut că desenul nu ar putea avea totuși și anumite explicații de altă natură, dar eu nu le-am găsit ȋn timpul căutărilor mele (destul de superficiale, recunosc).
Dacă tot am căutat, perimteți-mi să vă prezint un rezumat al contextului cultural găsit, context pe care îl veţi putea căuta și dvs. pe internet. Conform Wikipedia, desenul respectiv apare ca reprezentare prima dată în 1949 la autorul rus de orientare ezoterică P. D. Ouspensky, în încercările sale de explicare a teoriilor învăţatului mistic armean G. I. Gurdjieff, idei preluate şi extinse de către bolivianul Oscar Ichazo în teoriile sale despre personalitatea umană (enneagrama tipurilor de personalităţi). Eu nu le-am citit, dar dacă sunteți curioși, găsiţi un scurt istoric al subiectului pe site-ul The Enneagram Institute, la Learn – Traditional Enneagram (History), pe care-l puteţi accesa pornind de pildă de la adresa https://www.enneagraminstitute.com/how-the-enneagram-system-works/, dar şi pe Wikipedia, de pildă căutând Fourth Way enneagram). Oricum sursele de pe internet ce conectează acest desen cu lumea spirituală par nesfârşite (pe lângă unele desene minunate, mie cel mai mult mi-a plăcut o întrebare: Este Papa Francisc împortiva enneagramei?). Ȋn domeniul psihologiei există și ȋn limba română o mare bogăție de surse despre eneagrama personalităților. Revenind la matematica noastră, un lucru este sigur, tot ce am scris în acest aliniat nu are nici o minimă legătură cu lecţia prezentată pentru clasa a 5-a, şi în nici un caz nu ar trebui să ajungă la elevi.
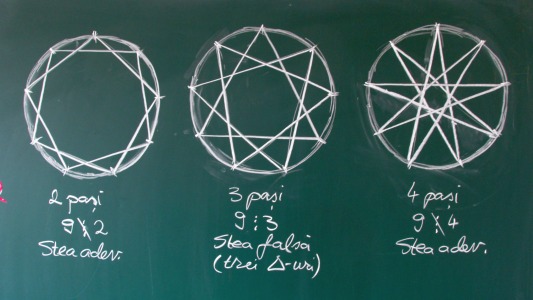
Tehnic, deși lipsește din dex-uri, cuvântul eneagramă desemnează o „stea cu nouă colţuri”. Astfel, pe lângă nonagonul regulat, sub denumirea de eneagramă (sau nonagramă) există două stelări cu 9 colţuri şi o stea falsă compusă de fapt din trei triunghiuri echilaterale (stele adevărate cu pas de 2 sau de 4 pentru că 9 nu este divizibil cu 2 sau 4, respectiv o stea falsă corespunzând pasului de 3 pentru că 9 este divizibil cu 3).
Pe lângă aceste eneagrame cu mecanism simplu de generare, am văzut că mai există şi ciudata eneagramă compusă din poarta lui 7 și un triunghi echilateral ce unește multiplii lui 3. Despre aceasta, pe mine mă interesează doar partea matematică, fără nici cea mai mică legătură cu teoriile mistico-ezoterice, unele de găsit la adresele mai sus menționate. Singurul lucru care mă miră este felul cum a putut fi adusă această reprezentare grafică de la nivelul pur rațional (al ȋmpărțirii cu 7) la nivelul de simbol spiritual. Misticul Titus