De curând a avut loc pe facebook un schimb de replici între profesori de matematică, despre rezultatul discriminantului. Ca persoană atentă la trăirile elevilor, am rezonat desigur cu următoarea afirmaţie: În școală, cea mai mare satisfacție o aveam când îmi dădea Δ-pătrat perfect (din câte am reţinut, afirmaţia îi aparţine d-lui Cristinel Mortici).
M-a bucurat această afirmaţie pentru că reprezenta o amintire pură venită din sufletul unui elev, o amintire despre o stare pe care cu toţii am trăit-o: ca elevi ne bucuram atunci când ne dădea pătrat perfect la delta. Cine nu recunoaşrte această stare trăită în timpul liceului, acela de fapt şi-a pierdut definitiv copilul din el. Copilul se bucură din oficiu pentru un rezultat frumos, îl resimte ca pe o confirmare a faptului că a lucrat corect.
Mă încântă deosebit astfel de afirmaţii rămase în sufletul unora ca amintiri de nezdruncinat; adulţi matematicieni (sau nematematicieni) care ne pot aduce trăiri din viaţa lor de elev, trăiri ce aduc astfel de amintiri ca într-o bulă nedistorsionată de anii vieţii (facultate, maturizarea deplină, şuişurile şi coborâşurile inerente).
Un elev care merge înainte când discriminantul nu dă pătrat perfect, fără măcar să verifice încă o dată, acela dă dovadă de o atitudine nesănătoasă. Între comentariile din acel moment chiar a apărut ideea: În liceu am avut doar 10 la mate, cu excepţia unei singure note de 8, pe care am încasat-o la un extemporal în clasa a IX-a pe trimestrul III, fiindcă nu mi-a dat DELTA pătrat perfect! Greşisem la calcule, evident (afirmaţie a d-lui Marcel Ţena, dacă nu am greşit la salvarea setului de comentarii).
Aceste observaţii, despre bucuria unui rezultat frumos, le cunoştea desigur şi profesorul Grigore Gheba: şi acum elevii se bucură atunci când obţin acele rezultate frumoase din exerciţiile sale, fie la cele cu fracţii etajate, fie la cele cu fracţii algebrice.
Nu vreau să reiau în această postare toate comentariile de atunci, ci prefer să închei cu o afirmaţie gen banc (din câte am reţinut, postat de către dl Costel Balcau): Ne păcălești, cum să fie triunghiul ăla pătrat? Titus Grigorovici, un veşnic copil
P.S. Această postare se doreşte o atenţionare la adresa celor care susţin de obicei că orice rezultat este unul bun, cu alte cuvinte susţinând “egalitatea de drepturi” a rezultatelor frumoase cu a rezultatelor urâte. Tehnic o fi aşa, dar în sufletul elevilor rezultatele frumoase îi atrag spre exersarea matematicii, pe când cele urâte nu. O persoană, profesor la clasă sau autor, care-şi bombardează elevii cu rezultate “indiferente”, de fapt îi îndepărtează de bucuria adusă de rezultatele frumoase. Într-o astfel de atmosferă, unii învăţăcei reuşesc să stea cu sufletul către matematică, alţii nu. În sine, această situaţie nu ar fi o mare problemă (“de fapt nu toată lumea trebuie să ştie matematică!”, s-ar putea spune) dar problema mare iese la iveală atunci când conştientizăm legătura indisolubilă între matematică şi formarea gândirii raţionale, respectiv lipsa acesteia din urmă la mult prea mulţi români.
Bucuria rezultatului frumos apare şi la teorema lui Pitagora, atunci când ai de extras radicalul în final: oricine se bucură dacă găseşte în acel moment un număr pătrat. Dacă este vorba de calcule cu numere mai mare, atunci la acel moment intervine speranţa că acel număr este pătrat. Eu folosesc acest moment dându-le elevilor probleme cu triplete pitagoreice mai mari, altele decât clasicele (3,4,5) sau (5,12,13), sau amplificări lor. Iar când a treia latură este un număr prim mai mare, lucrurile devin de-a dreptul palpitante. Oricum, la calcule lucrurile sunt simple şi clare: elevul se bucură atunci când într-un exerciţiu obţine un rezultat frumos.
Pe de altă parte, se poate pune întrebarea despre ce ar reprezenta ideea de rezultat frumos în cadrul proprietăţilor geometrice. De pildă, teorema lui Pitagora este oare într-adevăr un rezultat frumos, aşa cum gândeau egiptenii antici, care considerau egalitatea respectivă drept o adunare divină? Sau, faptul că suma unghiurilor unui triunghi este egală cu un unghi alungit (mult mai elegant decât numărul 180o), respectiv suma unghiurilor unui patrulater este egală cu măsura unei rotaţii complete, şi asta indiferent dacă patrulaterul este convex sau concav? Dar, mai ales, cum facem ca în momentul predării unor astfel de proprietăţi, să reuşim să le transmitem elevilor ideea de rezultat frumos?

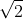 şi BC=2
şi BC=2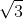 . Pe planul dreptunghiului se ridică, în punctul D o perpendiculară pe care se ia un punct P. Se consideră de asemenea M şi N picioarele perpendicularelor din A respectiv C pe dreapta PB, despre care se ştie că MN = 1. Să se calculeze lungimea segmentului (PB).
. Pe planul dreptunghiului se ridică, în punctul D o perpendiculară pe care se ia un punct P. Se consideră de asemenea M şi N picioarele perpendicularelor din A respectiv C pe dreapta PB, despre care se ştie că MN = 1. Să se calculeze lungimea segmentului (PB).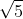 . Notăm cu A, B respectiv C ariile celor trei triunghiuri dreptunghice MNP, MPR şi NPR, iar cu D aria triunghiului MNR. Demonstraţi că A2 + B2 + C2 = D2.
. Notăm cu A, B respectiv C ariile celor trei triunghiuri dreptunghice MNP, MPR şi NPR, iar cu D aria triunghiului MNR. Demonstraţi că A2 + B2 + C2 = D2.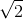 . La această problemă căutaţi două demonstraţii: una pe bază de tehnică de calcul algebric, iar cealaltă pe bază de elemente curate de geometrie, prin împăturirea succesivă a unei coli de hârtie, fără a scrie nimic (demonstraţie indiană de tipul: se vede!).
. La această problemă căutaţi două demonstraţii: una pe bază de tehnică de calcul algebric, iar cealaltă pe bază de elemente curate de geometrie, prin împăturirea succesivă a unei coli de hârtie, fără a scrie nimic (demonstraţie indiană de tipul: se vede!).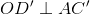 , O fiind centrul bazei ABCD.
, O fiind centrul bazei ABCD.