Următoarea problemă am descoperit-o încercând să-i explic unui elev anumite detalii de fineţe legate du unghiul diedru:
Luăm o coală de format A4 şi îi notăm colţurile cu A, B, C, D astfel încât latura [AB] să reprezinte lungimea dreptunghiului ABCD. Pliem apoi coala de-a lungul diagonalei [BD], astfel încât triunghiul BCD să rămână pe planul mesei, iar triunghiul ABD să se ridice până când punctul A ajunge deasupra laturii [DC], adică până când proiecţia ortogonală a punctului A pe planul (BCD) să aparţină lungimii [DC]. Determinaţi în această situaţie măsura “unghiului diedru” format de planele (ABD) şi (BCD).
C.T.Grigorovici, 9 ian. 2020
*
Înainte de a ataca această problemă este recomandat să studiaţi şi să vă încălziţi cu următoarele trei probleme de geometrie plană, rezultatele cărora (din câte văd eu) trebuind utilizate la problema principală. Este evident că întreg pachetul poate fi folosit minunat în pregătirea pentru olimpiadă.
1) Dacă împăturim o coală A4 în două” obţinem o coală A5. Două coli A4 alăturate, cu lungimea comună, formează o coală A3. Una din condiţiile de “funcţionare” a sistemului de formate A (A3, A4, A5 etc.) este cerinţa ca dreptunghiurile respective să fie asemenea. În această condiţie demonstraţi că raportul lungimii faţă de lăţime este obligatoriu egal cu 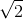 . La această problemă căutaţi două demonstraţii: una pe bază de tehnică de calcul algebric, iar cealaltă pe bază de elemente curate de geometrie, prin împăturirea succesivă a unei coli de hârtie, fără a scrie nimic (demonstraţie indiană de tipul: se vede!).
. La această problemă căutaţi două demonstraţii: una pe bază de tehnică de calcul algebric, iar cealaltă pe bază de elemente curate de geometrie, prin împăturirea succesivă a unei coli de hârtie, fără a scrie nimic (demonstraţie indiană de tipul: se vede!).
2) Considerăm cubul ABCDA’B’C’D’. Găsiţi legătura dintre secţiunea diagonală ACC’A’ şi problema precedentă, iar apoi demonstraţi că 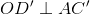 , O fiind centrul bazei ABCD.
, O fiind centrul bazei ABCD.
3) Fie paralelogramul ABCD în care alegem punctele M şi N mijloacele laturilor [CD] respectiv [AB]. Demonstraţi că segmentele [AM] şi [CN] împart diagonala [BD] în trei segmente congruente. Şi invers, adică diagonala [BD] taie “medianele” [AM] şi [CN] în segmente în raportul 1:2.
*
La începutul anilor ’90 exista încă o adevărată isterie când venea vorba despre denumirea unghiului diedru. Cerinţa oficială de denumire – absolut corectă, de altfel – era următoarea: determinaţi măsura unghiului plan corespunzător diedrului format de planele (ABD) şi (BCD). Să analizăm puţin fondul acestei exprimări. Unghiul reprezintă o figură geometrică plană (2D, cum s-ar spune acum), pe când diedrul reprezintă figura geometrică corespunzătoare în spaţiu (3D, în exprimarea modernă). Măsura deschiderii unui unghi plan este lămurită din clasa a 6-a. Pentru deschiderea unui diedru (3D) nu există o teorie nouă, ci măsura acestei deschideri se determină prin transferul pe un unghi plan (2D), un unghi între două semidrepte.
O singură “hibă” are întreaga teorie: esprimarea respectivă este mult prea lungă pentru a fi folosită în viaţa de zi cu zi. Toată lumea spunea de fapt: determinaţi măsura unghiului diedru format de planele (ABD) şi (BCD), dar această prescurtare prezenta celui care o folosea o vulnerabilitate clară în faţa unei alte persoane de a fi criticat pentru că nu s-a exprimat corect. Iar pedanţi “ultra-ortodoxi”, vânători de greşeli de exprimare, dispuşi imediat a te critica, din aceştia nu duceam lipsă.
Din fericire, lucrurile s-au mai calmat, aşa încât prin anul 2000 nimeni nu se mai obosea să folosească exprimarea riguroasă, toţi acceptând deja “unghiul diedru”. Eu prezint la clasă aceste observaţii la fiecare clasă a 8-a, mai ales pentru înţelegerea fenomenului de către elevii buni.
Există în general două categorii de probleme cu unghi diedru. În primul rând sunt cele în care se cere unghiul diedru între un plan “înclinat” şi un plan “orizontal” în figura respectivă, de pildă între o faţă laterală şi planul bazei la o piramidă. Astfel de probleme intră “în materia de examen” pentru note mari la EN. Pe lângă acestea există apoi şi probleme în care se cere unghiul diedru între două plane “înclinate”. Este de aşteptat ca astfel de cerinţe să nu se dea la EN, dar la olimpiade pot veni liniştit.
Există şi o altă clasificare posibilă. La problemele din prima categorie, mai ales la cele din corpurile regulate studiate, unghiul diedru căutat ne apare format de două triunghiuri isiscele, astfel încât perpendicularele din cele două plane să meargă pe dreapta comună în acelaşi punct (într-o piramidă patrulateră regulată VABCD, Apotema piramidei VM şi apotema bazei OM nimeresc amândouă în milocul muchiei bazei). O problemă în care cele două perpendiculare duse natural în figura respectivă nu nimeresc în acelaşi punct pe dreapta de intersecţie a celor două plane, o astfel de problemă creşte automat dificultatea situaţiei. O astfel de problemă este cea din această postare.
Iar dacă tot am ajuns la elevii buni, în altă ordine de idei, cândva în primăvara clasei a 8-a îmi propun să lămuresc – măcar pe scurt – şi existenţa piesei lipsă din alt “tablou”. Anume, că noi vorbim de diedru şi de tetraedru, dar nu vorbim de hexaedru, de octaedre, dar mai ales nu vorbin de triedru. Oare ce este acela un triedru? Eu am un astfel de obiect şi îl duc elevilor, doar aşa pentru cultură generală, cu precizarea că aşa ceva nu este în materia şcolară, deci nici pentru examen. CTG

Triedru este o figură geometrică formată din trei planuri care se intersectează două cîte două, avînd fețele mărginite de trei semidrepte care pornesc din punctul comun al celor trei planuri.
Da, cam aşa ceva, iar despre acesta doresc să vă prezint câte ceva uimitor în curând. CTG