La întrebarea “Pentru ce învăţăm matematica?”, sau la altele similare cum ar fi “La ce ne ajută matematica?”, venită din partea elevilor sau din partea unor părinţi ( acei care nici ei nu au avut o relaţie tare amicală cu matematica), la astfel de întrebări cei mai mulţi profesori răspund cu clasicul “Îţi trebuie la examen!” (la BAC, la EN etc.). Când discuţia este reluată la nivel mai înalt, să zicem într-o dezbatere la o emisiune televizată, sau între specialişti, la nivelul politicii educaţionale a statului român, atunci argumentele se ridică la nivelul olimpiadelor, subiectul fiind alăturat celor din categoria mândriei naţionale, a orgoliului de a fi parte a unui învăţământ super-performant la nivelul olimpiadelor internaţionale, pe baza argumentelor de tipul “Noi şi olimpicii noştri!”.
Cu diferite ocazii, în scrierile mele, am avertizat că această politică educaţională nu este sănătoasă, aducând totodată şi scurte argumente în susţinerea părerilor exprimate. De fiecare dată însă, părerea mea era susţinută doar de argumente raţionale de bun simţ, dar care puteau fi combătute pe baza clasicelor idei inoculate în mentalul naţional (al profesorimii, dar şi al unei mari părţi a populaţiei culte), inoculate de către aparatul de propagandă oficială în anii ’80 şi continuat “într-o mare bucurie” şi cu multă mândrie naţională în anii ’90, totul sub sloganul deja amintit: “Noi şi olimpicii noştri, noi şi sportivii noştri: Nadia, Hagi & Co. + renumiţii anonimi cu rezultate de vârf la OIM etc.”.
De câteva ori am precizat chiar că nu consider că sistemul olimpiadelor şcolare este dăunător, ci doar absolutizarea sa şi ridicarea acestei absolutizări la nivel de politică de stat în domeniu educaţional. Oricum, în această direcţie efervescenţa s-a mai liniştit, mai ales după rezultatele echipei României la OIM 2018 Cluj, rezultate considerate de ziariştii avizi de scandal drept slabe (să meargă ei acolo şi să vadă cum este să “iei în faţă” o problemă pe care nu o poţi urni din loc). Singurul aspect pentru care ar putea fi considerate slabe este faptul că nu au mai putut alimenta orgoliul naţional. Ei bine, şi ce facem acum? Nimic, ce să facem? Problema sistemului olimpic este una, iar aceasta în nici un caz nu poate fi echivalată cu problema situaţiei matematicii şcolare la nivelul maselor (aşa cum greşit au interpretat diferiţi jurnalişi, cum am spus, avizi de scandal).
Până acum nu am luat în discuţie subiectul în cauză într-un mod mai serios, mai structurat şi pe baza unor “argumente ştiinţifice”. Nu am avut energia sufletească să o fac, nu am avut forţa să mă pun “în gura lumii”, să mă pun într-o opoziţie oficială cu autorităţile. Nu am avut însă nici argumente mai “ştiinţifice”, dar nici vremurile nu erau “coapte” pentru un astfel de demers. Cei mai mulţi se simţeau încă “bine-mersi” în vechea paradigmă implementată de Ceauşescu şi aparatul comunist de propagandă după 1980, şi neluată în discuţie, ci continuată cu mare mândrie după Revoluţie. Numărul contestatarilor, dar şi al argumentelor împotriva sistemului dominat de politici elitiste, numărul acestora nu ajunsese la un prag critc care să ducă la acceptarea unei discuţii oficiale şi la luarea în calcul a unor gânduri de schimbare.
Despre partea cu “vremurile coapte”, în sensul acceptării unei astfel de dezbateri, situaţia începe să se schimbe. Dezbaterile generate de publicarea rezultatelor studiului PISA 2018 au arătat că societatea este deja pregătită pentru luarea în discuţie într-un mod serios a subiectului “Învăţământ orientat dominant elitist vs. învăţământ orientat pentru marea masă a populaţiei şcolare”. Doamna Viorica Dăncilă, cu renumita ei gafă cu aria cercului, a pregătit doar terenul, a încălzit minţile şi a pornit dezbaterile despre starea învăţământului. Publicarea rezultatelor PISA s-a mulat perfect pe această stare generală de indignare.
Mai rămâne partea cu “argumentele ştiinţifice” împotriva politicilor educaţionale orientate în primul rând – uneori exclusiv – după preocupările elitiste, în vederea potenţării olimpismului şcolar pentru vârfuri, sau în general în vederea pregătirii şi a rezultatelor la examene (EN & BAC). Din păcate, nu există “studii ştiinţifice” în România (sau în alte ţări) despre care să am cunoştinţă, care să susţină părerile despre nocivitatea unui sistem oficial dominant elitist (poate or fi, dar eu nu am cunoştinţă de aşa ceva). De curând însă am dat peste o “lege” recunoscută în mod ştiinţific la nivel internaţional şi care susţine aceste puncte de vedere. Interesant este că am aflat de această lege tot prin toamnă, fapt care mă face să susţin ideea unor “vremuri coapte” în sensul luării în discuţie a subiectului. Următorul pasaj (trei aliniate) este preluat şi tradus de pe Wikipedia (vezi https://en.wikipedia.org/wiki/Campbell%27s_law ).
*
Legea lui Campbell este o observaţie (*) dezvoltată de Donald T. Campbell, un psiholog şi cercetător sociolog […], care susţine următoarele: “Cu cât un indicator social cantitativ oarecare este folosit mai mult pentru luarea deciziilor, cu atât mai mult acesta va fi subiectul presiunilor coruptive (*) şi cu atât mai mult deciziile vor fi distorsionate (*) şi denaturate, chiar corupte (*) de către procesele sociale pe care indicatorul respectiv avea intenţia a le monitoriza.” Nu prea se înţelege! Haideţi să revenim în zona noastră de comfort, haideţi să revenim măcar în jurul şcolii.
Despre educaţie, Campbell scria în 1976: “Testele de evaluare a asimilării (*) pot fi foarte bine indicatori valoroşi despre nivelul atins şi despre asimilarea generală şcolară în condiţiile predării normale în direcţia competenţelor generale. Dar când rezultatele la teste devin scopul procesului de învăţământ, testele îşi pierd valoarea de indicatori ai stadiului educaţional şi ajung să deformeze procesul educaţional în moduri de nedorit. (Efecte similare apar desigur la testele de final ale diverselor cursuri sau la examene de admitere.)”
Principiul sociologic al lui Campbell este utilizat în a demonstra consecinţele negative ale testelor de evaluare la nivel naţional în şcoli. Aceste consecinţe pot lua, de pildă, forma predării pentru testare (teaching to the test) sau a învăţării pentru înşelare directă a evaluării (*outright cheating în original). […] Legea lui Campbell îi ajută pe oameni să înţeleagă de ce programele “Race to the top (cursă spre vârful ierarhiei)” al administraţiei Obama sau “No Child Left Behind Act (nici un copil lăsat în urmă)” al administraţiei Bush au deseori ca rezultat împietarea (*) şi nu îmbunătăţirea rezultatelor procesului educaţional.
(*) Traducerea acestor rânduri din engleză este destul de dificilă, deoarece textul original de pe Wikipedia foloseşte diferite cuvinte fără o clară corespondenţă în limbajul uzual românesc. Îmi cer scuze în cazul în care traducerea nu mi-a reuşit în modul cel mai fericit.
*
Cu alte cuvinte, legea lui Campbell reprezintă o observaţie de bun simţ despre felul în care acţionează anumite mecanisme sociale în contextul introducerii evaluări rezultatelor unor activităţi. Concret, legea lui Campbell vorbeşte despre adaptarea naturală a individului la faptul că va fi evaluat de către superiorii săi. Cu cât evaluarea este mai clară şi mai punctuală, cu atât activitatea se va îndrepta mai mult înspre aspectele ce vor fi evaluate, ducând la neglijarea aspectelor neincluse în evaluare. În lumea asta încă nu a fost inventată evaluarea perfectă; evaluările sunt eşantionare, iar existenţa unei liste de itemi de evaluat duce automat la adaptarea activităţii generale preponderent spre activităţi legate de acei itemi. Asta duce, la rândul său, la neglijarea automată a celorlalte activităţi, a itemilor şi a competenţelor ce nu sunt evaluate în procesul de evaluare. Ca urmare, educaţia nu mai este generală, completă şi atotcuprinzătoare, ci devine îndreptată doar spre aspectele ce urmează a fi evaluate. Astfel, educaţia devine incompletă, întregul proces generând lipsuri tot mai profunde în obţinerea unui rezultat educativ complet şi eficient.
Haideţi să luăm un exemplu pe care s-ar putea să-l mai ţină minte mulţi colegi. În cei doi ani cât am fost blagosloviţi cu tezele unice, la clasa a 7-a anunţându-se că se dă la teză până la lecţia cutare, cercul cu lungimea şi aria sa nefiind incluse în materia pentru teza unică pe semestrul al II-lea, clase întregi nu au mai învăţat această lecţie, deci nici nu aveau habar despre numărul pi (acei tineri termină sau chiar au terminat între timp facultăţile, ca să avem o relativă orientare în timp). Cei care au mai recuperat-o în clasa a 8-a au salvat tema cu pricina, dar la vremea respectivă oricum se vorbea că nu se dau corpurile rotunde, aşa că …
Da! Asta spune legea lui Campbell. Ar merita acum să luăm şi să citim acastă lege, cât şi consecinţele sale, prin prisma organizării orelor de matematică în vederea rezultatelor la examenele de evaluare la sfârşit de ciclu (EN sau BAC) şi a evaluărilor pe parcurs fără relevanţă asupra traiectoriei şcolare (EN-2 şi EN-6), dar vă las pe dvs., stimaţi cititori să faceţi singuri o astfel de analiză, bazată pe gândurile personale. Ţinând cont de importanţa total exagerată dată timp de peste un sfert de secol rezultatelor la olimpiade, putem desigur include într-o astfel de analiză şi predarea pentru rezultate la olimpiade în cazul unor profesori sau chiar în cazul unor şcoli întregi. Să încerc totuşi şi eu câteva rânduri în acest sens.
Decenii la rând de “picurare” în mentalul profesorimii matematice a ideii de “pregătire pentru examene şi concursuri” a dus la organizarea predării, a orelor şi a programelor în sensul respectiv. Elevii nu mai învaţă matematică pentru a dobândi o gândire raţională şi logică, ci pentru că le trebuie la examen. Aceasta are desigur şi o consecinţă colaterală de o relevanţă uriaşă pentru evoluţia generală a societăţii româneşti: cei care nu au nevoie de matematică la examen, aceia au tot dreptul să nu mai înveţe matematică deloc! Chiar şi cei care vor avea matematică la BAC, pot lua o “pauză” în clasele 9-10, pentru a se apuca apoi prin a 11-a de recuperat. Cum se descurcă în clasele 9-10? Mai copiază, mai fentează, o mai “scaldă”, …; văd ei cum trec, se descurcă cumva, educându-se de fapt în bunul stil românesc de a nu-ţi face treaba.
Dar chiar şi cei conştincioşi, cei care învaţă regulat, chiar şi aceştia învaţă doar ce ştiu că le va trebui la matematică. Astfel, mulţi elevi învaţă ordonat metodele de rezolvare pentru teste, după care le uită pur şi simplu. Foarte puţini sunt cei care mai învaţă matematica “de bucurie”. Nimeni nu mai învaţă subiecte care nu sunt în materia de examen. “Instituţia cursurilor opţionale” nu a prins în şcoli cu adevărat, fiind la cheremul profesorilor de matematică, care sunt de obicei preocupaţi doar de pregătirea examenelor sau a concursurilor, fiind evaluaţi de către şcoli sau de către inspectorate doar în acest sens.
Nimeni nu te evaluează ca profesor cât de raţional gândesc şi se exprimă elevii tăi în viaţa de zi cu zi, cât de bine pot aplica gândirea sau alte elemente din matematică în afara matematicii, ce capacitate au ei de a gândi în avans, cât de ordonat scriu sau cât de clare şi frumoase sunt figurile lor geometrice. Ca urmare, nici profesorii nu se mai preocupă de formarea unei gândiri raţionale şi logice la elevi.
Profesorul este preocupat de parcurgerea materiei şi de includerea în oră sau la temă a cât mai multor probleme posibile de venit la examene sau la concursurile fixate ca obiectiv cu cei mai buni elevi din clasă. Matematica nu mai este un instrument în mâna profesorului pentru formarea gândirii viitorilor adulţi, ci este doar o cantitate de cunoştinţe ce trebuie încărcate în mintea elevilor pentru a fi apoi verificate la examene. Sigur că pregătirea concursurilor duce această formă de încărcare la cote de multe ori inimaginabile de maltratare psihică şi mentală a elevilor. În acest sens eu nu înţleg cum de până acum nu s-a sesizat UNESCO despre situaţia de abuz matematic din România.
În această preocupare generală doar pentru examene şi concursuri au dispărut din materia şcolară multe exemple sau teme întregi foarte eficiente în formarea gândirii, doar pentru că au fost scoase de pe lista celor ce se pot da la examen. Mai rău, după reforma uitată din 1980 au dispărut din predare chiar şi metodele formatoare de gândire la elevi, metode verificate şi perfecţionate de-a lungul timpului (predarea în spirală, predarea intuitivă, predarea prin problematizare etc.). Cam aşa arată trecutul nostru.
Putem însă să ne uităm şi în viitor şi să ne imaginăm cum ar putea evolua predarea la matematică, dacă în curând ar deveni oficială şi deci obligatorie predarea înspre îmbunătăţirea rezultatelor la viitoarele teste PISA. Profesorii angajaţi ai diferitelor edituri ar selecta cum s-ar pricepe diferite “probleme de tip PISA”, le-ar include în “teste de tip PISA”, toţi profesorii ar parcurge astfel de teste, dresându-i pe elevi în acest sens, iar rezultatele la viitoarele studii PISA ar creşte simţitor. Ca urmare, administratorii ministerului învăţământului ar fi lăudaţi şi totul ar părea rezolvat. Sau, poate, dimpotrivă, organizatorii testării PISA s-ar sesiza şi ar schimba problemele într-un mod neaşteptat şi neprevăzut de autorii respectivi, dând sarcini pentru care elevii n-au fost pregătiţi prin acele culegeri. Atunci să vezi circ şi scandal!
Mai ţineţi minte, de pildă, “distracţia” cu problema despre vârsta ciobanului dată de două ori în Elveţia? O redau relativ din amintire: Un cioban are 36 de oi şi 7 capre. Ce vârstă are ciobanul? O mare parte din elevi au dat răspunsul 43, deşi problema nu se putea face (acesta fiind răspunsul corect). Scandal! Învăţători şi profesori revoltaţi! “Nu am făcut cu elevii aşa ceva la clasă.” Ok, au zis organizatorii. La următoarea testare apare o nouă problemă, ceva de tipul: Un cioban de 24 ani are 26 de oi şi 12 capre. Ce vârstă are ciobanul? O mare parte din elevi au dat răspunsul 62, adunând cele trei numere. Din nou scandal şi dascăli revoltaţi, dar din partea organizatorilor o tăcere de tipul: q.e.d. Ce putem vedea noi în acest exemplu? Analfabetism funcţional în domeniul lecturii, dar şi în direcţia matematicii, deşi elevii erau pregătiţi în vederea unor astfel de teste. Sau poate ar trebui să spunem: “datorită” faptului că elevii erau pregătiţi ţintit spre astfel de teste.
Revenind la oile noastre, pardon, la matematica noastră, să lămurim lucrurile cât se poate de clar: nu evaluările la nivel naţional (EN&BAC) şi nici olimpiadele şcolare nu sunt de vină pentru starea actuală a matematicii şcolare româneşti, ci absolutizarea importanţei pregătirii examenelor şi a concursurilor, cât şi presiunea asupra profesorilor pentru rezultate la acestea, aplicate ca politică oficială timp de atâţia ani. Astfel, profesorii nici nu mai ştiu cum să predea fără această motivaţie, iar elevii oricum de mult nu mai vor să înveţe în lipsa unui astfel de obiectiv (dacă învaţă, pentru că de mult a devenit o preocupare cvazi-naţională găsirea formelor prin care elevii să fenteze sistemul, să ia note cât mai bune şi să treacă examenele, fără să înveţe în mod corespunzător). Mai profund gândind, constatăm că nu pregătirea pentru examene sau pentru olimpiade este dăunătoareîn sine, ci orientarea procesului educativ tot mai mult înspre pregătirea acestora. La o analiză mai exactă, constatăm chiar că materia şcolară suferă de aranjări nenaturale unui proces sănătos de învăţământ (aranjat de exemplu pe principiul intuitivităţii), doar pentru a veni în întâmpinarea procesului de excelenţă (de pildă, partea de calcul de arii şi volume care nu intră pentru simularea din martie în clasa a VIII-a, doar pentru a lăsa loc studiului poziţiilor dreptelor şi a planelor în spaţiu, materie mult mai potrivită olimpiadei din februarie).
Indiferent de cum o luăm, situaţia în învăţământ este foarte complicată. După părerea mea însă, o analiză învăţământului românesc care să nu ia în considerare legea lui Campbell este din start sortită eşecului, la fel ca şi toate celelalte reforme în cascadă cu care ne-au cadorisit diriguitorii învăţământului românesc în ultimul sfert de secol. Sau poate ar trebui să spun: de peste 40 de ani? Pentru că Ceauşescu a fost primul care a direcţionat învăţământul românesc înspre încălcarea acestei legi, destul de proaspăt enunţate la vremea respectivă. Dar, ce-l interesa pe Ceauşescu de aşa ceva? El avea cu totul alte priorităţi. Vinovaţi cu adevărat sunt doar diriguitorii învăţământului de după Revoluţie, pentru că au păstrat linia dictatorului şi nu au studiat obiectiv situaţia pentru a lua măsurile ce se impuneau. Constantin Titus Grigorovici (& Co.)
P.S. La adresa https://searchbusinessanalytics.techtarget.com/definition/Campbells-Law , pe lângă două exemple concrete, găsim şi o variantă mai clară: Legea lui Campbell este observaţia că, odată identificată o măsurătoare ca indicator principal al succesului, capacitatea sa de a măsura cu exactitate succesul tinde să fie compromisă.
La adresa https://en.wikipedia.org/wiki/Goodhart%27s_law găsim o „lege” similară. Astfel, legea lui Goodhart reprezintă o altă observaţie în acest sens, denumtă după economistul Charles Goodhart care, prin 1975 a susţinut că: Atunci când o măsurătoare devine ţinta, aceasta încetează a mai reprezenta o măsurătoare bună (“When a measure becomes a target, it ceases to be a good measure.”)
Un subiect ceva mai îndepărtat, dar totuşi cu o oarecare relevanţă în discuţia de faţă, puteţi găsi sub titlul de efectul cobra, de pildă la adresa https://en.wikipedia.org/wiki/Cobra_effect.


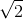 . La această problemă căutaţi două demonstraţii: una pe bază de tehnică de calcul algebric, iar cealaltă pe bază de elemente curate de geometrie, prin împăturirea succesivă a unei coli de hârtie, fără a scrie nimic (demonstraţie indiană de tipul: se vede!).
. La această problemă căutaţi două demonstraţii: una pe bază de tehnică de calcul algebric, iar cealaltă pe bază de elemente curate de geometrie, prin împăturirea succesivă a unei coli de hârtie, fără a scrie nimic (demonstraţie indiană de tipul: se vede!).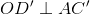 , O fiind centrul bazei ABCD.
, O fiind centrul bazei ABCD.