Găsirea numărului π este un proces ce poate fi prezentat elevilor de gimnaziu, cu abordare atât dinspre perimetrul cercului, cât şi dinspre aria cercului. În prima parte a acestui eseu am prezentat o formă de “găsire” a acestui număr, căutat dinspre perimetrul cercului, pe baza determinării prin măsurare a raportului între perimetru şi diametru (transversala sau lăţimea cercului). Tot în prima parte am prezentat şi o formă de demonstrare a formulei pentru aria cercului, dedusă însă indirect, adică din formula de perimetru. A fost o formă vizuală cu abordare predominant geometrică, deşi aceasta poate fi adaptată şi într-o abordare tehnicist algebrică (consider însă că cei care doresc o astfel de abordare ar putea-o prezenta în continuarea primeia, ca o formă de traducere în noul limbaj de lucru algebric ce se prefigurează în clasa a 7-a). În această a doua parte a eseului voi încerca prezentarea unor abordări directe pentru obţinerea formulei de arie a cercului şi deci pentru obţinerea unei aproximări a numărului π, căutând de fapt de câte ori intră suprafaţa pătratului razei în suprafaţa cercului
În prima parte a eseului am văzut însă o despărţire clară a două linii de preocupare: prezentarea din start a formulelor pentru perimetrul şi aria cercului, cât şi a numărului π, ce deschid posibilitatea de lucru pe exerciţii şi probleme, în vederea pregătirii testelor (utilitatea acestor formule), cât şi în paralel pornirea unui “proces de cercetare” pentru cunoaşterea diferitelor căi de obţinere a acestor formule şi a valorii aproximative de 3,14 pentru acest număr fascinant. Prima linie de preocupare este evidentă: toată lumea le dă elevilor formulele şi valoarea aproximativă a lui π şi se ocupă de aplicaţii ale acestora în exerciţii şi probleme. Cât despre cea de-a doua linie de preocupare, recomand parcurgerea câtorva căi de obţinere a numărului π, atât din motiv de formare a obişnuinţei de a înţelege “de ce este ceva aşa cum este”, cât şi ca exemple de gândire matematică diversă (motiv pentru care recomand în general la toate marile teoreme, dar şi le unele exemple de probleme individuale, parcurgerea mai multor demonstraţii diferite; de pildă parcurgerea a cel puţin 3-4 demonstraţii diferite la teorema lui Pitagora).
Ca o paranteză de accentuare la ultimul aliniat, vreau să atrag atenţia: cu cât parcurgem mai multe rezolvări diferite la o problemă, cu atât mai mult dezvoltăm gândirea în matematică şi prevenim obişnuinţa elevilor de a învăţa pur şi simplu rezolvări automat pe de rost. Desigur însă că nu ne putem permite mai multe rezolvări la toate problemele, dar măcar la cunoaşterea marilor probleme ale omenirii ne putem lua timp pentru a parcurge câteva metode diferite, astfel încât elevul să primească prin acestea mari exemple de gândire.
Am spus că găsirea numărului π este un proces ce poate fi prezentat elevilor de gimnaziu, atât dinspre perimetrul cercului, cât şi dinspre aria cercului. Prima aproximare a numărului π este numărul 3 şi am văzut în prima parte a acestei prezentări cum putem obţine această aproximare din reducerea perimetrului cercului la perimetrul hexagonului regulat. O formă similară de aproximare brută a numărului π ≈ 3 se poate obţine şi din direcţia aproximării ariei, anume prin calculul ariei dodecagonului regulat, dar este evident deja că se naşte aici o mică problemă de ordonare a materiei.
Organizarea oficială a materiei pentru clasa a 7-a cuprinde de-abia la finalul clasei lecţii despre poligoanele regulate, iar acolo se discută doar despre triunghiul, patrulaterul şi hexagonul regulat, iar la acestea accentul studiului este asupra diferitelor lungimi şi a relaţiilor dintre acestea (în conexiune raţională sau iraţională). Despre celelalte poligoane regulate sau nu se discută, decât foarte puţin despre unghiuri. La aceasă lecţie se stă foarte puţin pentru că toţi se grăbesc să ajungă la lecţia despre lungimi (apotemă, raza cercului înscris sau circumscris etc.). Ca urmare elevii rămân cu o ceaţă totală despre celelalte popigoane regulate (pentagonul, octogonul, decagonul etc) sau despre ideea de cerc înscris sau cerc circumscris (cei mai mulţi profesori nici măcar nu se obosesc să le reprezinte figura cu cu cele două cercuri şi un poligon regulat. La ora actuală nimeni nu-şi mai propune să facă aceste construcţii cu elevii.
Pentru a găsi aproximarea lungimii cercului la 3 diametre am avut nevoie să cunoaştem hexagonul regulat şi faptul că acesta se descompune în şase triunghiuri echilaterale (isoscele şi cu un unghi de 60o). Acestea sunt noţiuni elementare de clasa a 6-a şi nu necesită cunoştinţe despre numere iraţionale. Pentru a ne apropia de aproximarea lui π la 3 trebuie să aproximăm aria cercului la o figură cu aria egală cu triplul pătratului razei; în acest sens avem nevoie de cunoaşterea dodecagonului (a poligonului regulat cu 12 vârfuri). Este absolut ciudat şi total neaşteptat, dar şi acesta poate fi cercetat din punct de vedere a unghiurilor la nivel de clasa a 6-a. În plus, acesta ne oferă o surpriză de proporţii din punct de vedere “filozofic”: dacă la hexagonul regulat putem calcula perimetru fără a fi nevoie de numere iraţionale (deşi aria implică iraţionalitatea), la dodecagonul regulat se poate calcula aria fără a avea nevoie de numere iraţionale (de bună seamă că perimetrul va implica iraţionalitatea, aşa că ideea nu mă interesează în contextul prezentului material).
Dacă nu cunoaşteţi încă de acest subiect, atunci nici nu vreau să vă răpesc bucuria de a calcula singuri aria dodecagonului. Trebuie să calculaţi aria unui triunghi din cele 12 în care se descompune orice poligon regulat, triunghiuri având cele două laturi egale cu raza cercului circumscris. Pornind de la unghiul la centru al unui astfel de triunghi, de 30o, şi determinând lungimea unei înălţimi pe o latură congruentă (nu apotema poligonului), de pildă, în triunghiul AOB să luăm înălţimea din A pe raza [OB], se poate calcula apoi aria dodecagonului, obţinând ca rezultat 3r2 (rezolvare de cel mult două rânduri).
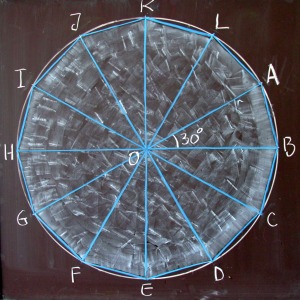
Consider că acest rezultat cu figura şi calculul aferent se potrivesc deosebit de bine în prezentul context, vizualizând – cel puţin pe cale algebrică – într-un mod fascinant aria de trei pătrate de rază, dar mai ales diferenţa minoră până la aria cercului, adică de fapt “cum arată” 0,14 (cele 12 bucăţele care arată ca bucăţile de unghii tăiate). Singura întrebare serioasă legată de aria dodecagonului regulat este legată de cum a putut profesorimea să piardă din conştienţa generală această informaţie. Eu am aflat-o dintr-o carte nemţească din timpul războiului, iar aceasta este singura sursă unde am găsit respectiva informaţie. (în cartea respectivă problema este abordată geometric; apropos: în mod similar, am aflat de la un prieten, profesor în Klagenfurt, cum în Austria s-au scos cândva după război multiplii de unităţi deca şi hecto, dar a rămas kilo, iar actualmente profesorii nu ştiu de ce există multiplicitate de 10 pe secvenţa mili-centi-deci-unitate, dar multiplicitate de 1000 pe secvenţa unitate-kilo; dânsul a “descoperit” multiplii deca şi hecto într-o carte veche din timpul războiului şi vroia să ne povestească despre acestea la un curs, drept o mare găselniţă).
Dar sigur, pentru a prezenta această mică comoară cu aria dodecagonului, trebuie găsită o formă de a cunoaşte cu elevii din punct de vedere geometric poligoanele regulate până pe la 20 de laturi (la nivel de clasa a 6-a, nu la nivel de lungimi iraţionale). În acest sens se pot studia metode cu rigla şi compasul, dar şi metoda cu raportorul (care ne permit construcţia pe divizori ai lui 360, de exemplu a poligonului regulat cu 36 de laturi). Apropos de iraţionalitate: dacă tot este atât de îndrăgită, de ce nu se calculează în finalul clasei a 7-a şi aria octogonului regulat, că dă aşa de frumos şi uşor cu sin45o? Ar înţelege şi copiii ce-s acelea poligoane regulate, că din cele trei din programă nu se pricepe de fapt ce-s acestea în general (tringhiul şi pătratul sunt total atipice, iar hexagonul este ciudat prin regularitatea supraperfectă).
Aceasta ar fi deci prima formă de aproximare directă a ariei unui cerc, confirmându-ne că suntem din nou în apropierea acestui număr fascinant, care în cazul ariei ne spune de câte ori intră pătratul razei în suprafaţa cuprinsă de cerc.
Următoarea metodă de aproximare a ariei cercului şi a numărului π am dezvoltat-o intuitiv într-o oră în urmă cu câţiva ani. Este din nou o metodă practică de cercetare, de tip “laborator de matematică”, în care elevii trebuie să lucreze ceva mai practic. Este o abordare frontală a problemei, prin faptul că ne apucăm efectiv să numărăm pătrăţelele din interiorul cercului. Aceasta vine ca o abordare naturală dacă profesorul s-a îngrijit ca înainte să mai întreprindă astfel de momente de numărat sau determinat aritmetic numărul de pătrăţele din interiorul unei figuri geometrice (atât la finalul clasei a 5-a, cât şi recapitulativ la începutul studiului despre arii în clasa a 7-a). Deci, elevii trebuie să numere pătrăţelele din interiorul cercului, încercând să aproximeze cât mai bine aria cercului. O aproximare destul de bună se obţine dacă nu privim absolutist cerinţa de numărare a pătrăţelelor “din interiorul cercului”, privind situaţiile mai permisiv, anume prin numărarea unor “pătrăţele” şi dacă acestea ies puţin în exteriorul cercului, echilibrând astfel suprafeţele abandonate din interior (veţi vedea imediat la ce mă refer).
Pentru asta vom trasa un cerc cu raza de 5 cm pe caietul de matematică cu pătrăţele. Am ales raza de 5 cm intenţionat, deoarece acest cerc mai are încă opt puncte “de coordonate întregi” prin care trece, câte două pe fiecare sfert de cerc (datorită teoremei lui Pitagora şi a “triunghiului egiptean” cu catetele de 3 şi 4 cm care dau ca ipotenuză tot 5 cm pe raze oblice). Pentru determinarea ariei vom număra pentru început totalitatea centimetrilor pătraţi întregi, cât şi a pătrăţelelor de pe caiet reprezentând sferturi de centimetri pătraţi situaţi complet în interiorul cercului (zona roşie, respectiv pătrăţelele colorate în desen cu verde). Apoi vom lua la numărat restul pătrăţelelor, cele care sunt parţial în interior, parţial în exterior, aproximându-l pe fiecare, sau pe câte două împreună, cât se poate de bine la noi sferturi (aproximăm arcul de cerc cu o linie poligonală care merge când cum, adică în unele cazuri mai în interior, în altele mai în exterior). Se obţine astfel o suprafaţă poligonală cu aria determinabilă şi care aproximează optic foarte bine cercul ales. Din împărţirea ariei obţinute la r2 = 25 se vede că şi aproximarea prin calcul este una mulţumitoare (78 : 25 = 3,12).
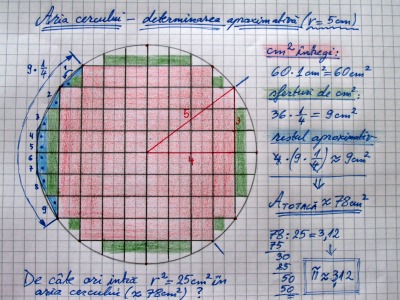
Desigur că putem analiza rezultatul muncii noastre, punându-ne întrebarea “de ce avem totuşi o eroare în minus de 2 sutimi?”. În cazul unei figuri meticulos realizată, la o analiză mai atentă se vede că suprafeţele pierdute prin aproximarea în interior sunt mai mari decât suprafeţele câştigate prin aproximarea în exterior.
Pentru eficientizarea muncii, consider că şi aici ar trebui lucrat tot pe o fişă preimprimată, altfel se pierde foarte mult timp cu făcutul figurii (ştiu din experienţă: deşi lucrez foarte mult cu clasele la realizarea figurilor, tot sunt mulţi elevi care se uită “ca mâţa-n calendar”, rămân în urmă şi “nu înţeleg”, iar apoi se duc acasă şi “se plâng” cât de grea-i matematica). Astfel, în vederea preîntâmpinării neînţelegerilor, elevii vor trebui să-şi facă doar însemnarea unităţilor de arie cu creioane colorate, să se concentreze asupra calculului centimetrilor pătraţi sau a pătrăţelelor, iar în final să facă însumarea suprafeţei şi împărţirea finală. Această lucrare practică ar putea fi dată ca sarcină într-o oră ulterioară (în nici un caz în prima oră despre lungimea şi aria cercului), la finalul orei sau combinată pe o fişă împreună cu alte sarcini mai obişnuite, cu exerciţii şi probleme (vedeţi în prima parte a eseului sfaturile de reluare preţ de câteva ore a exerciţiilor de bază, cât şi creşterea moderată a dificultăţii aplicaţiilor pentru o accesibilizare cât mai largă). Este evident scopul de a-l pune pe elev oarecum într-o stare de “cercetare” a acestui subiect, urmată de concluzia îmbucurătoare: “Uau, pot şi eu să mă apropiu de acest număr magic!”
În acest context este fascinant de cunoscut cu elevii cum au abordat problema ariei cercului vechii egipteni. Şi această metodă de determinare a ariei cercului s-ar potrivi de a fi inclusă în finalul unei fişe de lucru. Ca o paranteză fie spus, sunt conştient că prezentarea figurilor pe o fişă de lucru nu este tocmai cea mai strălucită idee în vederea obişnuirii elevilor cu construcţiile geometrice, dar îi ajută enorm să înţeleagă despre ce este vorba (foarte mulţi elevi nu au capacitatea de a extrage corect figura dintr-un text şi ca urmare abandonează, fapt recunoscut şi de organizatorii concursurilor naţionale care includ figurile geometrice în cadrul fişei de lucru cu subiectele). Se mai poate repara acest impediment dacă elevii primesc ca temă să refacă acasă figura şi calculul, copiate din fişă în caietul de matematică, construite exact cu instrumente.
Aşadar, cum făceau vechii egipteni? Informaţia vine tot din Papirusul Rhind şi sună ca o reţetă magică, ceva de felul următor (citat absolut orientativ din memorie, după diverse traduceri, care oricum sunt şi acestea doar orientative). Aşadar: Ia a noua parte (din lăţimea cercului), ia rezultatul de opt ori şi înmulţeşte apoi cu ce-ai obţinut. Asta este! (aria cercului). Elementele din paranteze nu existau de fapt în text, ci trebuiau subînţelese, iar “textul” era oricum hieroglific, departe de gândirea noastră actuală. Să recapitulăm în text clar, mai pe limba noastră: Ia a noua parte din diametrul cercului, înmulţeşte-o cu opt şi ridică la pătrat. Astfel ai obţinut aria cercului. Cu alte cuvinte, mai pe scurt spus, aria cercului ar fi egală cu pătratul a opt noimi din diametru. Scris pe limba noastră de matematicieni, am obţine formula:
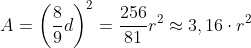 .
.
Rezultatul (aproximativ, desigur) este unul foarte bun pentru acele vremuri (având la împărţire a treia zecimală chiar zero). Asta la cca. 1500 de ani înaintea lui Arhimede, şi se pune clar întrebarea: oare, cum s-a obţinut această metodă? De la zei sau o aveau moştenită de la atlanţi? Lăsând gluma de-o parte, şi-au bătut matematicienii capul (în ultimul un secol şi jumătate) şi au ajuns la următoarea explicaţie plauzibilă.
Suprafaţa cercului este aproximată în doi paşi: în pasul I aria cercului este aproximată cu aria octogonului “treimilor” decupat din pătratul circumscris cercului iniţial; în pasul II aria acestui octogon este aproximată la aria unui pătrat cu latura de 8 (noimi ale diametrului cercului).
Pentru o înţelegere mai bună trebuie să luăm la început o “unitate dă măsură” a problemei, anume noimea diametrului. Apoi luăm pătratul circumscris cercului a cărui arie vrem să o determinăm, şi îl împărţim în 81 de pătrăţele, plecând de la unitatea stabilită. Tehnic, pentru primul pas, este suficient dacă luăm doar punctele de treimi ale laturilor (împărţind astfel pătratul în 9 subpătrate; acest aspect întâlnit în multe surse derutează însă spre finalul raţionamentului; eu am făcut desenul cu împărţirea în 9, dar pe o tablă cu pătrăţele, fiind astfel vizibile şi cele 81 de pătrăţele mici).
Pasul I este deja foarte evident, anume că aria cercului se aproximează foarte bine cu aria octogonului IJKLMNPQ: în unele zone iese octogonul în exterior, în altele iese cercul mai în afară, părând astfel că se echilibrează ca suprafeţe. De-abia la un calcul exact vedem o eroare infimă de trei sutimi în defavoarea octogonului (faţă de rezultatul cunoscut actualmente). Dar şi acest rezultat nu este unul de neglijat, având însă în plus avantajul unei clarităţi vizuale deosebit de simple a aproximării. În multe surse însă se rămâne doar la acest nivel, după care se dă rezultatul vechilor egipteni, A ≈ 256/81∙r2, cititorul rămânând astfel într-o ciudată ceaţă mistică a neînţelegerii (inclusiv în manualul german de care am vorbit în prima parte a eseului; şi într-o imagine prezentată în muzeul Palais de découverte din Paris m-am împiedicat de respectivul neajuns). “De unde?” se va întreba cititorul, pentru că rezultatul figurii cu octogonul este de forma A ≈ 28/9∙r2.
Pasul II ne ajută în acest sens, şi doar făcând această nouă aproximare a ariei octogonului într-un pătrat cu latura de opt unităţi (printr-o ciudată adăugare de o unitate de arie, pe baza apropierii lui 63 de pătratul 64), doar aşa vom putea face pasul spre rezultatul din Papirusul Rhind. De ce a simţit nevoia învăţatul antic să facă şi acest al doilea pas, asta nu cunosc, dar putem da cu presupusul. Oricum, rezultatul îmbunătăţeşte puţin eroarea, de la o lipsă de trei sutimi la un adaos de două sutimi. Aşadar, combinând cei doi paşi, deducem că aria cercului de diametru 9 este aproximată la aria pătratului de latură 8, aceasta fiind în esenţă metoda egipteană.

Includerea acestei metode în finalul unei fişe de lucru ar avea scopul ca pe baza figurilor pre-existente în fişă elevii să refacă calcului şi să obţină în final aproximarea lui π, însoţită automat de acea cunoscută stare de uimire, scurtă dar intensă. Cu alte cuvinte, elevii ar fi puşi din nou să guste puţin din starea de “cercetător”, după principiul “căutaţi aici şi veţi găsi ceva frumos!”.
Trebuie făcută aici o scurtă precizare. Aproximarea cercului prin octogonul treimilor din pătratul circumscris este în sine o deosebită realizare şi poate fi făcută separat (adică pentru început doar pasul I şi doar pe treimi). Ideea de a aproxima cercul cu o figură poligonală, idee din care a derivat apoi “cvadratura cercului”, această idee este una deosebită şi orice elev ar trebui să o întâlnească în şcoală într-o formă simplă şi accesibilă. Iar aproximarea cu acest octogon este, fără discuţie, deosebit de accesibilă. Ideea este foarte frumoasă chiar şi dacă octogonul respectiv nu este un octogon regulat, având doar unghiurile congruente, nu şi toate laturile congruente (acest aspect ar trebui inclus undeva înainte în studiul despre poligoanele regulate).
Dacă tot am adus vorba despre Arhimede (puţin mai sus), eu aş încheia aceste preocupări cu un scurt rezumat despre rezultatele sale în domeniu. Arhimede este considerat oarecum primul geniu universal al omenirii, personalitatea sa fiind disputată intens între fizicieni şi matematicieni. Aparent câştigă fizicienii pentru că matematicienii nu-i folosesc numele, dar, la vremea sa, din creaţia lui Arhimede rezultatul cel mai înalt a fost apreciat ca fiind măsurarea sferei, adică volumul şi aria sferei (se ştie că pe piatra sa funerară erau sculptate, întrepătrunse între ele, o sferă, un con şi un cilindru). Ca o paranteză, trebuie precizat că cele două rezultate, volumul şi aria, au venit în această ordine, cu alte cuvinte, rezultatul final şi cel mai uimitor este totodată şi cel mai simplu, anume că aria sferei este de patru ori aria cercului (de acelaşi diametru).
Legat de numărul π (desigur, nedenumit ca atare în acele vremuri), Arhimede a dat cel mai bun rezultat pentru următoarele peste 1500 de ani, rezultat care se apropie extrem de bine de aproximarea acceptată ca uzuală în vremurile moderne. Anume, Arhimede a aproximat π ≈ 22/7 (anticii nu cunoşteau fracţiile zecimale) şi putem printr-o simplă împărţire verifica faptul că această fracţie ordinară aproximează numărul π corect la primele două zecimale (de abia la miimi apare eroare). Consider că acest rezultat trebuie neapărat dat elevilor, punându-i totodată să-l verifice.
Cum a reuşit Arhimede acest rezultat? Calculul este unul laborios şi depăşeşte cu mult nivelul gimnazial, dar le putem spune elevilor că acest calcul se bazează pe aproximarea ariei cercului cu aria unui poligon regulat cu 96 de laturi. De ce 96? Păi, plecând de la dodecagonul regulat, Arhimede a construit prin înjumătăţirea arcelor (adică prin bisectoare) în mod succesiv poligoane regulate cu un număr dublu de laturi, deci cu 24, 48 şi în final 96 de laturi. Nu am făcut calculul respectiv, aşa că nu pot spune dacă Arhimede s-a oprit aici considerând rezultatul unul suficient de bun (poligonul cu 96 de laturi aproximând extrem de bine cercul), sau s-a oprit aici pentru că a găsit un rezultat foarte frumos în fracţia 22/7, evident frumos prin simplitatea sa (următoarele aproximări mai exacte ale lui π prin fracţii ordinare sunt de ordinul sutelor, acestea fiind evident mai greu de memorat; dacă nu greşesc: 331/106 şi 355/113).
Există aici o precizare (eventual cu trimitere în urmă), având un clar iz practic: elevii se pot apropia de înţelegerea aproximării cercului printr-un poligon regulat cu multe laturi, dacă au realizat în prealabil un astfel de poligon. De pildă, am fi putut să le propunem elevilor spre finalul studiului despre poligoane regulate, despre care am vorbit mai la începutul acestui eseu, sau dimpotrivă, le putem propune chiar acum, în asociere cu prezentarea despre aproximarea dată de Arhimede, să construiască un poligon regulat cu 36 de laturi folosind un raportor (cel mai bine un raportor complet de 360o, care evită eroarea asamblării din două semicercuri). Astfel, împărţind cercul în 36 de arce de câte 10o şi construind poligonul corespunzător, elevii vor pricepe imediat cât de bine aproximează acesta de fapt cercul respectiv. Ca observaţie practică, este evident aici că trebuie lucrat cu creion de 0,5 sau oricum cu un creion foarte bine ascuţit. După acest desen elevii vor privi cu mult mai mare admiraţie şi respect realizarea lui Arhimede bazată pe împărţirea cercului în 96 de părţi egale şi aproximarea cercului cu poligonului regulat obţinut.
*
În final doresc să revin la analiza lecţiei deschise ţinute în toamnă. Este evidentă greşeala de strategie, prin care am încercat să înghesui atâtea şi atâtea informaţii într-o singură oră, covârşindu-i pe elevi cu o cantitate năucitoare. Dorind să fac cât mai mult, am impus o viteză peste posibilităţile majorităţii elevilor, aceştia reuşind doar să copieze ce venea de pe tablă către ei, fără însă a putea şi trece conţinuturile prin filtrul propriei înţelegeri. Este o greşeală general întâlnită, şi un aspect apărut deseori ca reproş la adresa noastră, a profesorilor de matematică. Această atitudine îşi are originea în anii ’80 când s-a marşat mult pe creşterea cantităţii şi a nivelului de lucru la clasă, în vederea obţinerii rezultatelor la olimiade şi concursuri (desigur, în contextul politic general al unor astfel de cerinţe la adresa întregii societăţi; cei care au trăit atunci îşi mai aduc aminte de veşnicele raportări de depăşiri de plan sau de îndepliniri a planului de producţie înainte de termen).
Dar, să privim şi “partea plină a paharului”: dacă nu ar fi fost întâmplarea cu această lecţie nereuşită, cine ştie cât aş mai fi amânat să “pun pe hârtie” toată această colecţie minunată despre numărul π (doar la nivel gimnazial). Şi aşa mi-a fost foarte greu, mi-a luat cam jumătate de an să găsesc forma în care să scriu toate aceste lucruri şi mai ales timpul şi energia pentru a o face.
Legat de parcurgerea tuturor acestor exemple şi informaţii, mult peste ce fac la clasă majoritatea dascălilor, am certitudinea că elevii mei, care au parcurs aceste elemente, au dezvoltat o mult mai bună înţelegere a fenomenului şi în general o gândire superioară celor care au primit doar formulele şi le-au aplicat direct ca pe nişte reţete. De pildă, elevii care s-au ocupat într-adevăr să numere cm2 şi pătrăţelele din interiorul unui cerc au dezvoltat evident o mult mai bună înţelegere a noţiunii de arie în general, cât şi a deosebiri majore între figurile cu laturi drepte şi cerc în ceea ce priveşte exactitatea determinării ariei (cei care doar au copiat de pe tablă, şi nu s-au străduit măcar acasă să înteleagă ce s-a întâmplat, desigur că nu au beneficiat de această ocazie pentru dezvoltarea gândirii).
Accentuez că ne-am preocupat aici de cunoaşterea şi înţelegerea unor fenomene ce ţin de cultura generală (de pildă noţiunea de arie), pe când lecţiile oficiale (despre poligoane regulate şi cerc) se îndepărtează cât pot mult de cultura generală, trăgând preocupările cu toată înverşunarea înspre zona abstractă de specialitate (de pildă făcând o apologie a iraţionalităţii). Ca o paranteză fie spus, este evident ajutorul oferit de întâmplarea cu “idioţenia numită aria discului”, observaţia respectivă oferindu-mi ocazia de a lămurii înainte de toate chestiunea lejerităţii limbajului (vezi postarea din martie 2020 la adresa http://pentagonia.ro/despre-idiotenia-numita-aria-discului/).
Cum ar trebui să procedăm la predarea acestei mega-lecţii? Păi, fie reuşim să alocăm acestui subiect câteva ore şi parcurgem materia aşa cum am prezentat-o în acest eseu, fie facem lecţia pe scurt şi includem restul materialului în fişe de lucru suplimentar, pentru acasă, prin care elevii să facă totuşi cunoştinţă cu toate aspectele prezentate. Poate totuşi ar fi mai bine să facem fişele de lucru combinate pentru clasă şi acasă, aşa cum am prezentat în acest eseu, stratificate desigur, fiecare fişă pe nivele de accesibilitate şi de aplicabilitate (fiecare fişă la început cu exerciţii simple, apoi cu exerciţii de complexitate mai ridicată, iar în final cu o parte de “cercetare” pe exemplele date; astfel, fiecare elev lucrează cât poate, dar are în final satisfacţia că a făcut măcar ceva; în plus, puse în această ordine şi elevii din pluton au satisfacţia că ajung şi ei până la sfârşitul fişei, chiar dacă au “goluri” pe parcurs). Astfel aranjate, aceste fişe ar putea fi folosite şi în contextul predării de la distanţă, aşa cum se cam vede că va trebui să facem în viitor (am evitat folosirea verbului “se prevede”, acesta fiind de obicei asociat unor “ordine de sus”). CTG
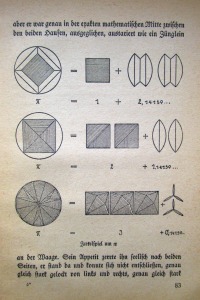
P.S. M-am gândit că ar fi de interes, ca o curiozitate, să aruncăm o privire în cărticica menţionată în care am găsit informaţia despre aria dodecagonului regulat. Autorul este Graf Ulrich, iar lucrarea se numeşte Kabarett der Mathematik, (Ed. Ehlermann, Dresda, 1943). Ulrich Graf abordează problema din punct de vedere pur geometric (nu cum v-am îndrumat eu, adică amestecat geometrico-algebric); o abordează printr-un şir de imagini, la modul cel mai brut, anume prin descompunerea suprafeţei discului în bucăţi care sunt apoi reasamblate în formă de trei pătrate şi un rest. Am încercat la început şi eu această cale, dar respectul faţă de demonstrarea riguroasă a diverselor aspecte implicate m-a forţat la mulţi paşi demonstrativi (lejer o pagină mare de demonstraţie, cu care am pierdut însă la vremea respectivă interesul aproape întregii clase). Iată, deci, cum pune autorul problema respectivă:
Legendarul număr π, aşa cum învăţăm la şcoală, ne spune de câte ori poate intra pătratul razei în cerc. Să încercăm această doar geometric, fără nici un calcul, ci doar cu rigla şi compasul. O dată merge fără nici un effort; şi de două ori putem construi pătratul din cerc, păstrând încă un rest respectabil. Iar dacă ne străduim o vreme, vom putea obţine chiar şi trei pătrate (cu raza cercului ca latură) din suprafaţa cercului, pentru că dodecagonul regulat (12-unghiul sau 12-gonul, cum se spune în germană) se poate descompune în exact trei astfel de pătrate. Un rest mic ne rămâne şi vedem fără niciun calcul: π trebuie să fie 3 şi încă un mic rest, fiecare amintindu-şi aici din timpul şcolii: π = 3,14159… = 3 + 0,14159… = 3 + un rest. Aşa am ajuns în jocul nostru să o reîntâlnim pe bătrâna Doamnă Matematica, jonglând între geometrie şi aritmetică, iar fiecare îşi poate alege ce i se potriveşte mai mult ….
Alăturat găsiţi imaginile de care vorbesc şi modul ciudat de concret de a vizualiza întrebarea “câte pătrate ale razei intră într-un cerc?” (inclusiv o încercare de-a mea de lămurire a ultimului pas, cel cu trei pătrate).

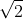 şi BC=2
şi BC=2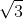 . Pe planul dreptunghiului se ridică, în punctul D o perpendiculară pe care se ia un punct P. Se consideră de asemenea M şi N picioarele perpendicularelor din A respectiv C pe dreapta PB, despre care se ştie că MN = 1. Să se calculeze lungimea segmentului (PB).
. Pe planul dreptunghiului se ridică, în punctul D o perpendiculară pe care se ia un punct P. Se consideră de asemenea M şi N picioarele perpendicularelor din A respectiv C pe dreapta PB, despre care se ştie că MN = 1. Să se calculeze lungimea segmentului (PB).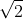 şi BC=2
şi BC=2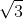 . Fie M şi N picioarele perpendicularelor din A respectiv C pe diagonala [BD]. Calculaţi diametrul cercului ştiind că MN = 1.
. Fie M şi N picioarele perpendicularelor din A respectiv C pe diagonala [BD]. Calculaţi diametrul cercului ştiind că MN = 1.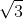 . Determinaţi măsurile următoarelor unghiuri: a) unghiul dintre dreptele PC şi MN; b) unghiul dintre dreapta PM şi planul (ABC); c) unghiul diedru dintre planele (PBC) şi (ABC).
. Determinaţi măsurile următoarelor unghiuri: a) unghiul dintre dreptele PC şi MN; b) unghiul dintre dreapta PM şi planul (ABC); c) unghiul diedru dintre planele (PBC) şi (ABC).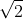 şi PN=
şi PN=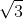 . Pe planul acestui triunghi ridicăm perpendiculara PR=
. Pe planul acestui triunghi ridicăm perpendiculara PR=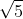 . Notăm cu A, B respectiv C ariile celor trei triunghiuri dreptunghice MNP, MPR şi NPR, iar cu D aria triunghiului MNR. Demonstraţi că A2 + B2 + C2 = D2.
. Notăm cu A, B respectiv C ariile celor trei triunghiuri dreptunghice MNP, MPR şi NPR, iar cu D aria triunghiului MNR. Demonstraţi că A2 + B2 + C2 = D2.

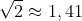 şi
şi 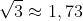 cu aproximările lor uzuale cu două zecimale exacte. Verificând pe aceste aproximări suma lor 1,41 + 1,73 = 3,14, putem vedea ciudăţenia cea mai mare:
cu aproximările lor uzuale cu două zecimale exacte. Verificând pe aceste aproximări suma lor 1,41 + 1,73 = 3,14, putem vedea ciudăţenia cea mai mare: 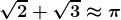 .
.

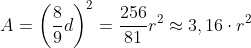 .
.

