O mare parte din orele din şcolile româneşti se fentează, o prea mare parte. În actualul an şcolar parcă am resimţit mai tare ca oricând acest fenomen. Ca de obicei, toţi actorii implicaţi poartă câte o parte din vină: părinţii nu-şi aduc copii la şcoală uneori, extinzându-se fenomenul plecării în concedii în timpul şcolii; profesorii au şi ei momente când au alte gânduri decât să vină la ore; cât despre autorităţile ce ne organizează activitatea, uneori te gândeşti că n-au ceva mai bun de făcut decât să anti-organizeze un bun mers al învăţământului. În aceste condiţii desigur că şi elevii încep de la o vreme să chiulească. Am strâns câteva gânduri pe această temă, iritat find de faptul că simt cum îmi este afectată strădania de a-mi face treaba cât de cât eficient (mai ales cu aceşti copii distruşi de folosirea abuzivă a ecranului de la vârste tot mai mici, dar şi de prea mult timp petrecut în online în pandemie – aici fiecare la nivelul său de vârstă cu alte efecte). Mai ales la matematică, acolo unde totul este mai dificil, pe fondul presiunii examenului, atmosfera de fentat ore din jur mă deranjează profund. Iată deci eseul meu despre arta de a nu face ore în şcoli.
*
Marţi 20 dec. 2022 (înainte de vacanţa de Crăciun), într-una din pauze (probabil la ora 11) o colegă a venit în sala profesorală vădit indignată şi ne-a citit următorul mesaj primit de la învăţătoarea fiului ei (înscris la altă şcoală): Stimaţi părinţi, mâine miercuri 21 dec. copiii vor veni la şcoală fără ghiozdane; vom face activităţi informale legate de Crăciun. Joi 22 dec. copiii vor face activităţi legate de Crăciun acasă.
Ca în fiecare an, înainte de fiecare vacanţă, colega respectivă este indignată pentru că la şcoala noastră nu se prea poate lua vacanţă înainte. De obicei unii colegi încearcă să sugereze elevilor zile libere suplimentare şi ca urmare unii părinţi, de obicei de la clase primare, fac scurte reclamaţii la direcţiune, după care Directorul scrie câte un mesaj de “băgat minţile în cap”. Mai ales pe învăţătoare le loveşte chestia asta mai puternic, pentru că desigur există întotdeauna părinţi care muncesc (sau au activităţi pregătitoare pentru sărbători) şi nu au cu cine lăsa copilul acasă, iar aceştia se prevalează de “dreptul lor constituţional” la şcoală al copilului, forţând astfel învăţătoarele la “baby-sitting” până în ultima zi.
Ca şi de alte ori, şi acum colega respectivă a reuşit să stârnească colegii, aceştia aducând şi alte exemple în acest sens, de genul că la liceul cutare “din centru” marţi nu s-au trecut absenţe, iar joi toată lumea ştia că nu se vor face ore. La clasele mai mari lucrurile sunt simple: elevii chiulesc şi gata, dar şi pentru profesori e nasol, pentru că nu ştiu exact dacă au sau nu “clienţi” până în ultima clipă sau la ultima oră (când poate constată că au mai rămas doar doi).
La clasa a 8-a de anul acesta, colegul diriginte (profesor de română) a preîntâmpinat elegant lucrurile: a venit şi m-a întrebat de săptămâna precedentă ce fac cu orele de mate. I-am spus că le fac pe toate, luni predau iar miercuri de la 12-13, cât şi joi de la 11-12 facem aplicaţii la ultimele lecţii predate (exerciţii din testele de antrenament 2020). Joi au lipsit doi sau trei elevi, astfel că am putut face orele în cele mai bune condiţii.
Eu nu pot altfel: pur şi simplu nu aş suporta acea stare ciudată de vinovăţie. În plus, cum aş putea eu să le cer elevilor să-şi facă datoria dacă în paralel le-aş da chiar eu contraexemple de comportament. La fiecare sfârşit de semestru, trimestru, modul, sau cum le-o mai fi zicând, ajung să mă enervez pentru că societatea mă împinge într-o stare ce nu-mi convine. Mai nou, inclusiv înainte de minivacanţe, cum ar fi vacanţa de fasole cu sau fără cârnaţ, adică cea de Sf. Andrei + 1 Dec. + puntea corespunzătoare + weekendu’ aferent, discuţiile erau în toi: de ce ne mai aduce la şcoală luni şi marţi??? (oricât liber s-ar da, oameni vor şi mai mult!)
Da’, cine-i de vină pentru starea asta? Păi, la fel ca la seria de eseuri despre starea matematicii şcolare româneşti, şi aici există multipli vinovaţi: atât unii colegi dascăli cât şi din partea părinţilor există impulsuri spre a nu se mai face ore înaintea vacanţei. Evident că, la fel cum sunt dascăli care vor să-şi facă datoria, dar şi dascăli care doresc să chiulească, tot aşa există şi părinţi care vor să se facă ore, la fel ca şi părinţi care se gândesc că nu mai are rost, sau unii care-şi planifică plecări cu familia înaintea vacanţei oficiale. Şi desigur că şi elevii învaţă uşor în această atmosferă, atât de la adulţii din jurul lor, cât şi unii de la alţii.
Impulsurile spre nefăcut şcoală în zilele dinaintea oricărei vacanţe vin din toate părţile, inclusiv de la onor Ministerul Educaţiei. Cum? Păi – de pildă – ce au însemnat atâţia ani de Săptămâna “Şcoala altfel” lipită înainte de vacanţa de Paşte? Unii i-au spus “Şcoala pe dos” sau “Şcoala defel” sau cine ştie cum altfel. Oare de ce? Desigur că sunt mulţi colegi care se pricep să umple cu sens aceste zile, dar foarte mulţi încă nu ştiu “cu ce se mănâncă aşa ceva” CU SENS. Foarte mulţi au tradus această perioadă doar în sensul unor ieşiri în oraş sau în natură, excursii sau chiar tabere, pentru că atât s-au priceput, iar asta a dus la percepţia, la concluzia că activităţile din Săptămâna altfel sigur nu au voie a fi făcute în clasă. Fără să mai vorbim de haosul creat pentru cei care rămân în şcoală şi nu au profesori la diferite ore, pentru că aceştia sunt plecaţi cu alte clase (percepţia s-a extins pur şi simplu şi la nou apăruta Săptămână verde).
Pentru liceeni şi pentru elevii din clasele gimnaziale mari (adică pentru cei ce au ajuns să dezvolte o stare cât de cât realistă de şmecherie) este evident că asta sună clar a invitaţie spre chiul (nu are rost să mai vorbim aici despre cei din clasele a 12-a, care oricum vin la şcoală doar la materiile de examen).
În urma poveştilor cu care au venit elevii acasă, mai ales cei mici, despre ce s-a făcut sau nu în astfel de perioade, în familii s-a creat oricum percepţia că săptămâna “Şcoala altfel” este o zdravănă perioadă de pierdut vremea (de-a lungul anilor, de când s-a introdus). Ca urmare, mulţi părinţi decid să nu-şi mai trimită copiii la şcoală în acea săptămână; fie îi lasă acasă (dacă sunt mai mari şi pot sta toată ziua în faţa unui ecran, sau are cine să-i supravegheze), fie îi duc la bunici din weekend-ul precedent, fie îşi iau şi ei un binemeritat concediu şi “o taie” pe undeva cu familia, pentru că – nu-i aşa? – preţurile în turism sunt mai mici atunci. Oricum – cel puţin în Cluj, până când săptămâna respectivă se organiza centralizat, adică toţi de-o dată – fenomenul se putea observa la nivelul oraşului printr-o bruscă descongestionare a traficului de dimineaţă.
Ca în majoritatea altor domenii, şi în cazul Săptămânii “Şcoala altfel” se vede înclinaţia patologică a naţiunii noastre spre ceea ce Titu Maiorescu şi contemporanii săi au denumit aşa de frumos Teoria formelor fără fond. Aşa că – ce să faci? asta e! – cel mai bine nu mai mergem la şcoală în acele zile. Da, iar de anul acesta avem şi “Săptămâna verde”. Minunat! O creştere bruscă cu 100% a perioadei de flendurit şi de nefăcut ore în mod organizat, dictate “de sus”. de la organizatorii învăţământului, cu buna colaborare a dăscălimii, care doar atâta se pricepe (nota bene: n-am fost şcoliţi în acest sens defel!), dar şi cu minunatul sprijin al multor părinţi.
Până de curând titlul acestui articol ar fi fost cât de cât corect: Arta de a nu face ore înainte de vacanţă. Din păcate însă, fenomenul s-a extins masiv şi după vacanţă! De pildă, vineri în 6 ianuarie am fost anunţat telefonic de un părinte că “îmi spune deschis”: au o ofertă de nerefuzat la schi şi copilul este atât de pasionat de schi şi bla-bla-bla, aşa că ei îşi asumă şi copilul va absenta prima săptămână (nici nu mai discut despre “oare unde au mers?”, pentru că mai în toată ţara nu era zăpadă; doar în a doua jumătate a lunii ianuarie 2023 a început să fie raportată zăpadă în unele locaţii). Dar, staţi liniştiţi, din altă şcoală am aflat că profa de mate a lipsit prima săptămână pentru că a fost la schi (cu încă o colegă!). Curat minunat!
Dar, de fapt, ce tot vorbim aici despre înainte sau după vacanţă? După cum am spus deja, de ani buni lumea s-a obişnuit să-şi organizeze oricând concedii în timpul şcolii. Plecări în Thailanda sau în Malta, ori city-break-uri la Paris sau săptămâni de schi la Straja (Lupeni, Hunedoara), atunci când preţurile sunt mai mici, întoarceri din vacanţă cu întârziere “din State de la tata” sau plecări înainte de vacanţă în diverse ţări europene pe “motive personale”, de-a lungu’ Mediteranei sau de-a latu’ Europei, de toate am văzut în ultimii ani – nu inventez nimic!!! (cu pauză desigur în lockdown). Din bun simţ rezist tentaţiei de a insera aici şi ultimele destinaţii din aceste zile. Cum am spus, chiar şi din partea unor colegi dascăli am văzut aşa ceva, persoane care nici măcar nu se jenează să posteze “în timp real”, pe facebook cât sunt ei de fericiţi în Egipt, la piramide, în comparaţie cu “fraierii” care merg în continuare zilnic la lucru.
Întâmplarea de anul trecut cu familia respectivă ce au fost prinşi de poliţia germană cu copilul, iar ciudatii ăia de nemţi s-au trezit să verifice dacă în România este sau nu vacanţă, asta o cunosc toţi. Şi, ce s-a mai întâmplat în continuare? Pentru că nu-mi pot închipui că poliţia română să ia măsuri în acest caz, cum desigur nu acţionează defel în astfel de situaţii.
Ce-aş putea eu să fac într-o astfel de situaţie? Păi, veţi spune, pune-l absent pe elevul respectiv şi “te-ai spălat pe mâini”. Îl pun absent, dar ce rezolv, pentru că părintele are dreptul să-i motiveze o ciurdă de zile de absenţe. Şi oricum, la nevoie se merge la un medic sau la diriginte sau chiar “mai sus” şi “se rezolvă lucrurile” (la fel ca şi cu scutirile medicale ce camuflează chiulul unor elevi). Adevărul este că trăim într-un sistem – cel puţin cel de stat – care permite aproape oficial chiulitul. Iar atunci, ce să ne mai mirăm de activitatea la clasă?
Ţine de acest subiect desigur şi întrebarea clasică din mintea unora (puţini): dar cum este în alte părţi? Ceilalţi (cei mulţi) au deja un răspuns clar: du-te mă, că aşa e peste tot! Nu este aşa peste tot, puteţi fi siguri! Eu am apucat să întreb ocazional pe diferite persoane care au trăit în Anglia, în Statele Unite sau în Franţa, iar lista poate continua. Nu-i aşa! Nimeni nu lipseşte nici măcar o oră fără un motiv adevărat întemeiat, iar lipsitul se sancţionează drastic.
Povestind despre intenţia de a scrie acest articol unei familii prietene care a trăit câţiva ani în Statele Unite (o familie de intelectuali de vârf, domnul predând ca Profesor la o universitate de Top 3 mondial) am avut surpriza să-i văd stârniţi în acest sens mult peste aşteptările mele. Şi ei, după întoarcerea în România, s-au simţit agresaţi de-a lungul anilor de această atitudine generală de chiul, dând exemple în cascadă despre cum era starea de lucruri acolo.
Dar, de unde vine acest fenomen cunoscut de către orice român? Cred că există mai multe surse, chiar diferite paliere “istorice” ale acestora. Periada fanariotă, dar mai ales anii de comunism se pot alinia la discuţie în acest sens. Sau – cum am spus deja – Teoria formelor fără fond ar putea fi una dintre explicaţiile importante (şi aceasta venind dinspre atmosfera din secolele fanariote – multe rău ni se trage de atunci). Privind la nivel macro-european putem observa şi o relativă variaţie a conştiinciozităţii de la est la vest, cu interferenţe însă şi din partea sistemelor politice sau tradiţiilor spirituale. De multe ori incapacitatea organizatorică îşi spune cuvântul, dar cel mai important factor îl reprezintă tradiţia, care – din păcate – este transmisă cu mare sfiinţenie: aşa am fost obişnuiţi, aşa ştim şi aşa facem în continuare, iar cei ce vin după noi aşa învaţă şi ei!
Totuş, aş reveni la întrebarea de mai sus, doar că mai aplicat: de unde vine acest fenomen în cazul şcolilor? (pentru că pe mine această întrebare mă roade). Aici cred că putem găsi o explicaţie foarte plauzibilă. Sistemul birocratic le cerea profesorilor încheierea mediilor undeva la începutul ultimei săptămâni de şcoală din trimestru sau semestru, pentru ca situaţiile să poată fi centralizate pe şcoală şi raportate la inspectorat pentru centralizare pe judeţ şi probabil raportate mai sus. Deoarece însă sistemul nostru de învăţământ este construit pe “autoritatea notelor”, după încheierea mediilor în şcoli se instala un vid de autoritate. Desigur că mulţi profesor încheiau mediile chiar din penultima săptămână, aşa încât starea de “face fiecare ce vrea” apărea chiar dinainte. Această stare era accentuată, mai exact confirmată şi de faptul că raportările trebuiau să includă şi absenţele. Cu alte cuvinte, toată ţara ştia că în ultima săptămână nu se mai puneau absenţe sau note. Pe acest fond “naţiunea” s-a obişnuit că înainte de vacanţă se poate lipsi, pentru că “nu mai au ce să-mi facă”. Şi invers a început să evolueze fenomenul: de vreme ce astfel funcţionau lucrurile, nici profesorii nu mai făceau mare lucru la ultimele ore, această stare accentuând şi girând la rândul ei şi mai puternic fenomenul, ducând practic la un cerc vicios din care acum habar nu avem cum să mai ieşim (nu că tare mulţi s-ar dori să ieşim!).
Am criticat “Ministerul” în principiu pentru măsuri mai vechi sau mai noi, dar realitatea este că reforma din acest an, cu o singură perioadă de încheiere de medii, la care se adaugă şi raportarea absenţelor de-abia după vacanţă (de pildă absenţele pe decembrie au trebuit raportate de-abia la jumătatea lui ianuarie), în acest an nu ar mai fi trebuit să se înregistreze fenomenul conform apariţiei vidului de autoritate dinaintea vacanţei de iarnă. Din păcate obiceiul lipsitului de la şcoală, respectiv cel al nefăcutului de ore din această perioadă “s-a încarnat” atât de adânc în mentalul majorităţii, încât nu mai poate fi oprit. Toţi încercă să lipsească cum pot şi nimeni nu pune absenţe. Pe majoritatea oamenilor nu-i mai poate împiedica nimic să lipsească şi ei “măcar puţin”.
Dimpotrivă, anul acesta cei mai “pe fază” au ales oportunitatea unei noi vacanţe pentru toată lumea (cea de toamnă), în jurul căreia să mai lipească mici ieşiri. Elevii la care părinţii “n-au fost pe fază”, n-au avut ieşiri speciale în toamnă ratând oportunitatea, aceştia au venit la şcoală “nemţeşte”, până la ultima oră de vineri 21 octombrie 2022).
Aceleaşi idei se aplică şi în cazul zilelor libere naţionale, cum ar fi cea de 24 ianuarie, de “Mica Unire”, chiar şi dacă autorităţile au încercat să preîntâmpine fenomenul declarând şi ziua de 23 liberă ca “punte”, generând astfel 4 zile libere legate. Ţinând cont că tocmai a nins în sfârşit, măcar în munţi (după mijlocul lui ianuarie), oare câţi părinţi au decis să transforme în “vacanţă” prin prelungire aceste 4 zile, alipind şi altele (înainte de acest “weekend”, sau în continuarea sa)? Gestul autorităţilor de preîntâmpinare a fost intrpretat astfel de de către unii prinr-o invitaţie la o adevărată văcănţucă.
Revenind la săptămâna “Şcoala altfel”, ca un bun exemplu, eu aş pune în discuţie în primul rând abilităţile organizatorice, atât la nivel macro, cât şi la nivel micro. Nici sistemul oficial înalt, cu birocraţiile sale, nu au ştiut să organizeze clar (de pildă printr-un ghid detaliat), dar nici mulţi dascălii nu s-au priceput să pună în forme coerente astfel de activităţi. În plus, şi la interferenţa dintre cele două nivele lucrurile nu au funcţionat. Ideea unei perioade unice pe ţară s-a dovedit aiurea şi inpracticabilă. Nici forma unei săptămâni de acest tip la alegere centralizat pe şcoală nu are mult mai multă coerenţă; se stabileşte de către cei cu “gura mare” iar ceilalţi … (la fel se întâmplă şi în cazul “Săptămânii verzi”); nu intru în detalii în acest sens. Refuz să mai vin cu idei despre o mai bună şi mai coerentă organizare, dar oare nu ar fi mai eficient să fie lăsată o libertate totală asupra activităţilor de tip “altfel” sau “verde” profesorilor sau diriginţilor, aceştia trebuind doar să acopere de-a lungul unui an şcolar cele 5 zile corespunzătoare sau un număr de ore la fiecare clasă după cum se potriveşte mai bine în cazul fiecăruia? Zic şi io!
Reiau un exemplu în acest sens despre care am mai vorbit: în urmă cu mai mulţi ani, director fiind, a trebuit să mă duc la un inspector să cer semnătura de aprobare pe un dosar de tabără a unei colege învăţătoare la clasa a 3-a, care planificase o săptămână de activităţi agricole de toamnă cu toată clasa într-un sat renumit pentru păstrarea tradiţiilor rurale. În dosarul de planificare erau incluse diferite activităţi specifice perioadei la ţară, precum aratul, dar mai ales recoltatul, în primul rând culesul strugurilor şi băutul mustului proaspăt reprezentând desigur una cele mai importante activităţi. Şi, ce a avut inspectorul respectiv de comentat: de ce nu face colega asta tabăra respectivă în săptămâna “Şcoala altfel”?, care atunci era centralizat înainte de vacanţa de Paşte. (q.e.d.)
Dar, oare ce-am putea face noi – cei care vrem să ne facem treaba – pentru a ne apăra măcar parţial de acest flagel al lipsitului de la ore (cuvântul “chiulit” pare puţin depăşit) O idee ciudată ar fi să programăm teste importante în aceste zile vulnerabile la chiulit (de pildă la mate’). Asta ar funcţiona împreună cu ideea că orice test trebuie dat de toţi copiii, iar cei care lipsesc îl vor da cândva în viitor, când nu se aşteaptă, dar mai ales după suficient timp încât să apuce să uite, să se strângă suficientă materie încât mintea “vinovatului” să fie obligată să uite. Această metodă ar lovi însă şi în cei care au lipsit, de pildă pentru că într-adevăr au fost bolnavi (bat-o vina de gripă!, fără să mai vorbim de alte belele, cum ar fi mâine rupte etc.).
Nu ştiu ce putem face, dar văd că tupeul chiulitului este justificat deseori chiar de către familie; iar aici o parte mare din vină o au chiar politicienii. De pildă, de ce au voie părinţii să motiveze la liber “nu-ştiu-câte” zile, uite numai aşa, pentru ca să fie mulţumiţi şi să vină voturile? Sau, de ce să fie atâtea zile libere, care la rândul lor generează oportunităţi de lipsit?
Eu nu ştiu cum ar trebui să se facă, astfel încât să se remedieze acest flagel al chiulitului la nivel naţional, dar sigur văd că problema se extinde de la un an la altul, în loc să fie remediată (sentimentul meu ar aproxima situaţia deja la orientativ 25% din perioada şcolară).
Această stare de “nefăcut ore” se extinde masiv, primind tot mai multe motive oficiale de manifestare, chiar şi de justificare. Vacanţa de toamnă, cât şi Săptămâna “verde” reprezintă ultimele noi ocazii apărute în programul oricum încărcat al zilelor în care se poate lipsi de la şcoală. Iar ideea de a organiza vacanţa pentru “tabără de schi” decalat pe diferite judeţe a fost o încercare palidă de preîntâmpinare a fenomenului din partea Ministerului.
În general, aproape fiecare întrerupere a şcolii cu o perioadă de zile libere declanşează în mentalul oamenilor ideea oportunităţii de a lipsi, de a lipi câteva zile “auto-libere” de cele oficiale şi de a planifica acolo o distracţie, o călătorie, o “ceva”. În urmă cu 10-20 de ani aceasta se manifesta doar înainte de vacanţă, dar acum oamenii s-au deşteptat, şi le lipesc şi în urma vacanţei, tot mai des şi în jurul mini-vacanţelor sau a săptămânilor speciale în care este evident că nu se va sta în bancă şi să se facă şcoală “de-adevăratelea”.
Am aici şi un comentariu acid special la adresa acestui “mega-partid al părinţilor“: dacă faci doar şcoală tradiţională cu copiii, cu stat în bănci şi lecţii serioase, atunci mulţi comentează că nu faci “şcoală mai modernă”; dimpotrivă, dacă se dă liber oficial la încercări de a face “şcoală mai altfel”, atunci din nou vor veni uni şi vor comenta că nu se face “treabă serioasă ca pe vremuri” şi nu-şi vor mai aduce copiii la şcoală.
Am pornit acest articol în vacanţa de iarnă şi am lucrat câteva săptămâni la rând, dar l-am lăsat de-o parte pentru că mi se părea prea agresiv. Acum, când au înflorit pomii şi am avut mini-vacanţa de 1 Mai, acum pot doar să mă uit în jur şi să văd indignarea generală la adresa fenomenului în discuţie. Profesorii sunt disperaţi pentru că în această atmosferă nu se mai poate face şcoală “cum trebuie”. Mai ales în cazul matematicii aceste aspecte se simt deosebit de greu. Nu te-ai apucat bine de lucru, că şi trebuie să te opreşti. A ajuns aproape imposibil să se mai intre cu eficienţă în acea stare de muncă serioasă, pe care cei mai mulţi o cunosc dinainte de pandemie. Nu cred că pandemia are în sine o vină clară, dar sigur starea generală de nefăcut ore din Şcoala românească nu ne ajută să revenim la atmosfera serioasă de lucru dinainte de 2020.
După vacanţa de Paşte, după cele trei zile de ore, în şcoala soţiei mele a urmat Săptămâna “Şcoala altfel”, lipită de minivacanţa de 1 Mai (am auzit persoane de-a dreptul indignate că 1 Mai pică lunea, fără nici măcar o zi de punte!). Situaţii similare au fost în toate şcolile: o săptămână specială + 4 zile înainte de vacanţa de Paşte + vacanţa respectivă + 3 zile după + cealaltă săptămână specială + săptămâna de 4 zile de după 1 Mai = 5 săptămâni în care n-ai prea putut face mare lucru.
Oamenii îşi face deja calculele ce se va întâmpla de 1 Iunie şi de Rusalii (fără să mai discutăm despre şcolile unde există clase cu predare în limbile minorităţilor ce trăiesc pe alte calendare religioase şi care au şi ei “liber”; chiar aşa: şi de Ramaza Bayram de ce nu?, ca să fim politically-correct). Da, şi desigur ne apropiem de vacanţa de vară când mulţi se vor gândi să-şi ia vacanţă măcar cu o săptămână mai repede, desigur datorită ofertelor de preţ mai bune (sau din alte diferite motive personale).
Merită să evoc aici un exemplu ceva mai ieşit din comun, întâmplat în şcoala noastră. În urmă cu patru ani, o mămică şi-a luat fata de clasa a 8-a prin primăvară şi s-au dus pentru câteva zile (o săptămână?) la Ierusalim, în “Ţara Sfântă”, făcând asta exact în timpul simulărilor de la Minister pentru EN8 (cândva prin martie a fost asta atunci, în 2019). Eu am “ridicat o sprânceană” atunci şi m-am arătat indignat; fata era departe de a fi un elev de succes la învăţătură şi cumva am luat-o personal, drept o sfidare la adresa strădaniilor mele. Acum fata respectivă este în clasa a 12-a, tot la noi la şcoală, la uman, şi “ghici ciupercă” unde a fost plecată cu mamă-sa exact în săptămâna cu simulările oficiale pentru BAC. Da, aţi ghicit: o vizită la “locurile sfinte” rezolvă preventiv orice examen! Atâta vreme cât nu copiezi, orice metodă e bună ca să-ţi iei BAC-ul. Un pic de ajutor divin la momentul potrivit sigur nu strică în acest sens. Întâmplarea respectivă ne oferă de fapt o imagine despre cum văd unii părinţi învăţătura şi pe cei ce se ocupă cu aceasta. Titus Chiulus Liberus
P.S. În “liberele de Mica Unire” am avut o scurtă corespondenţă cu d-na despre care am scris mai sus, din familia ce au lucrat în Statele Unite pentru câţiva ani. I-am trimis articolul în forma de atunci iar dânsa mi-a răspuns a doua zi. Între timp eu n-am mai lucrat la articol până acum, când m-am uitat din nou la răspunsul său. Consider că merită prezentat complet:
Abia m-am trezit şi mi-a venit o idee de titlu. “Arta de a chiuli se învată din şcoală“, şi de încurajare a atitudinii de superficialitate în actul de învăţare şi de lâncezeala faţă de muncă în general. Responsabilii??? Toată lumea: Ministerul învăţământului, profesorii şi părinţii.
Când am povestit în vacanţa de iarnă cu familia respectivă pentru prima dată despre acest articol, dânşi şi-au dat drumul indignării şi s-au lansat într-o pledoarie (din care efectiv nu se mai puteau opri) despre cum era organizat “acolo, în State” totul, despre cum se făceau ore din prima zi, în şcoli fiind aplicat de la prima oră programul complet. Cât despre cum se porneşte anul şcolar “la noi”, asta într-adevăr nu am inclus în eseul de faţă. Pe scurt, am putea prezenta lucrurile după vechea vorbă: Românu’ greu se apucă de lucru, da’ şi când s-a apucat, repede se lasă! Iată ce scria în continuare doamna respectivă:
Anul şcolar are o structura fixă (pe semestre, săptămani, ore) care ar trebui respectată ad litteram. DAR … şi profesorii şi părintii şi elevii ştiu că în primele două săptămâni din noul an şcolar este debandadă: nu toate orele sunt acoperite de cadre didactice, aşa că cei prezenţi suplinesc pe cei absenţi, ore mai multe la o materie, mai puţine sau deloc la o alta, orarul este provizoriu şi se schimbă de la o zi la alta, se dau peste cap planificările profesorilor (cărora însa li se cere “să fie la zi cu programa”), unele manuale sunt insuficiente sau lipsesc cu desăvârşire, în unele şcoli înca se mai repară sau se văruiesc săli de clasa, etc. Şi dacă tot nu se face şcoală ca lumea în acele săptămâni … care-i problema pentru unii părinţi să-şi planifice concediul cu copii în acea perioadă?? Toate acestea sunt ultra cunoscute de către cei din Ministerul Învăţământului de zeci de ani, dar sunt tratate ca o boală incurabilă.
Apoi urmează o perioadă în care programul intră în normal, dar curând vin mini-vacanţele şi vacanţele… Alt motiv de a trata şcoala superficial şi de a încuraja chiulul. Grav mi se pare faptul că la nivel oficial în unele şcoli chiulul este acceptat chiar, nu se pun absenţe, nu se dau note, nu se fac ore în anumite perioade. Şi atunci, de ce ar lua părinţii structura anului şcolar în serios? De ce nu şi-ar programa concedii în acele perioade??
Şcoala este locul de munca al copilului şi felul în care evolueaza în cadrul acelui loc de munca îi trasează drumul în evoluţia lui ca adult la viitorul loc de muncă. Ca elev este interesat în primul rând de note, ca adult va fi interesat în primul rând de bani. Şi, bineinteles, să profite de orice posibilitate de a-şi oferi concedii sau beneficii suplimentare.
Ca o paranteză legată de manuale, merită să amintesc aici cum aproape 20 de ani capitolul despre patrulatere era cuprins în manualele de clasa a 6-a, dar de fapt se făcea în programa de clasa a 7-a. Iar oficial se spunea că “sunt manuale”. Dar să revenim la doamna respectivă.
UAU! Acestea sunt gândurile unei d-ne profesoare ieşită la pensie, ce a apucat să cunoască şi să aprecieze starea de bună ordine din şcoli peste ocean. Pentru cine se miră de ce este societatea noastră aşa cum este, aici aveţi un răspuns cât de clar posibil: asta educăm în şcoală, asta avem apoi în societate. Sau invers: şcoala ar trebui să reflecte visele noastre despre cum ne dorim să arate societatea. Oricum, le mulţumesc familiei respective pentru gândurile trimise, cât şi pentru susţinerea în redactarea acestui eseu. CTG
P.P.S. Mă bate gândul înspre ideea unui studiu asupra probabilităţii ca diferitele zile ale săptămânii să fie libere, ca să ştie cei interesaţi unde să-şi pună orele în orarul săptămânal. E clar că lunea şi vinerea conduc detaşat într-un astfel de top. Asta şi datorită liberelor de Paşte sau Rusalii, dar şi datorită principiului de punte aplicat altor zile libere ce apar la date fixe marţea sau joia. Oricum, chiar şi în lipsa unui studiu ştiinţific riguros, şmecherii cunosc de mult aceste aspecte. Ca o paranteză, dimpotrivă, dacă eu aş dori să-mi fac cât mai bine treaba fără să fiu afectat de acest sitem de anulare oficială a orelor lunea şi vinerea, atunci ar trebui să cer în toamnă, la făcutul orarului, să mi se pună de fapt orele cât mai mult marţi, miercuri, joi (dacă nu în totalitate). Desigur că într-o astfel de situaţie aş putea fi suspectat de colegi că vreau să-mi prelungesc regulat weekend-ul. Acum nu am timpul şi starea necesare pentru un astfel de studiu “profund matematic”, dar pot oferi în schimb un studiu “aritmetic” al situaţiei pe anul şcolar în curs. Astfel, în prezentul an şcolar avem următoarele date:
1) Per total sunt 27 săptămâni întregi şi 9 săptămâni fragmentate (“săptămâni” de 2, 3 sau 4 zile lucrătoare; una a fost chiar de 2+2 zile lucrătoare, cea din 3-7 octombrie, întreruptă de ceva gen ziua profesorului). Deci, 25% din săptămâni sunt incomplete, având “scris pe ele” cu litere mari invitaţie la chiul. Acest raport 27:9 = 3:1 este important în contextul în care şcolilor nu le este permis să aleagă în săptămâni fragmentate săptămânile speciale “Şcoala altfel” sau “Verde”. Cu alte cuvinte, şcolile sunt obligate să mai sacrifice încă două săptămâni neapărat întregi, de 5 zile, pentru cele două săptămâni speciale. Altfel spus, săptămânile “de frecat menta organizat” depăşesc în şcoala românească un sfert din anul şcolar.
Dacă mai tăiem măcar prima săptămână din anul şcolar (când treaba abia începe să pornească, oricum ziua de luni fiind sacrificată pentru serbarea de începutul şcolii, nefăcându-se astfel ore), cât şi ultima săptămână din anul şcolar (cine mai face atunci ore???), raportul ajunge la 23 săptămâni întregi de muncă, faţă de 13 săptămâni de cam-ne-muncă, reducând perioadele de muncit adevărat la două treimi din timpul anului şcolar. La acestea se mai adaugă desigur săptămânile în care elevii au Eveluările Naţionale la clasele 2, 4 sau 6, dar mai ales şi pachetele de 2 sau 3 zile de simulare la EN8 sau BAC, când clasele respective sigur nu mai stau la ore după simulare (minorităţile naţionale cu încă o zi în plus). În afara unor cazuri patologice, în săptămânile respective elevii măcar stau la şcoală în restul zilelor.
2) După cum am spus, nu am timp pentru un studiu matematic general valabil, dar haideţi să ne uităm totuşi şi la numărul zilelor de şcoală efectivă din prezentul an şcolar. 30 de zile de LUNI; 34 zile de MARŢI; 34 zile de MIERCURI; 34 zile de JOI; 32 zile de VINERI. Precizez că nu am luat în calcul prima luni din anul şcolar şi nici vinerea de 2 iunie ca posibilă punte cu recuperare. Apropos punţile date “liber cu recuperare”: ştie toată lumea cum se recuperează acestea. Concluzia este evidentă şi nu are rost să o mai enunţ. O gândiţi cu toţii în acest moment.
Aici putem conecta cu o ultimă idee “stranie”: în aceste condiţii, care-i logica conform căreia sindicatele cer măriri de salarii? Când de fapt, în actuala lipsă acută de bani, autorităţile “ne plătesc” cu zile libere, dar şi cu oportunităţi de zile de fentat suplimentar. Ciudat este că apoi societatea vrea “rezultate” şi se plânge de nivelul şcolii. Da’ de unde, “dragii moşului”?
Aş putea continua acest articol “la nesfârşit”, dar încerc să-mi impun un final. Sunt sigur însă că toţi cei care l-aţi citit veţi avea şi dvs. exemplele personale cu care să continuaţi discuţia cu cei din jur. Cum se poate face matematica în aceste condiţii? Vai de noi!




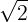 şi pe
şi pe 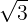 , importanţi pentru elevii de gimnaziu, fiecare cu câte 10 cifre zecimale, imprimate pe treptele ce urcă de la etajul 1 la 2.
, importanţi pentru elevii de gimnaziu, fiecare cu câte 10 cifre zecimale, imprimate pe treptele ce urcă de la etajul 1 la 2.




