În precedentele postări despre figura cu pătratele construite în exteriorul triunghiului dreptunghic ne-am concentrat asupra ideii de arie a acestora, scoţând în evidenţă descompunerea acestor pătrate în pătrăţele, adică în unităţi de bază. La acestea relaţia din teoremă se evidenţiază adunând conţinuturile celor două pătrate ale catetelor pentru a obţine pătratul ipotenuzei. În acest sens reamintesc traducerea ad-literam a cuvântului german pentru arie: Flächeninhalt = conţinutul suprafeţei.
Despre acest subiect am mai vorbit şi cu alte ocazii, de pildă în postarea din toamna lui 2018 http://pentagonia.ro/teorema-lui-pitagora-un-simbol-denaturat/ . Desigur că în exterior, pe laturile triunghiului dreptunghic se pot desena orice poligoane, cu condiţia să fie toate trei asemenea între ele (trei dreptunghiuri asemenea, trei triunghiuri echilaterale, trei pentagoane regulate etc.). Aceste construcţii ar fi însă potrivite, doar ca nişte curiozităţi, de prezentat mult după învăţarea teoremei lui Pitagora.
Mai am o poză găsită pe net în care însumarea pătratelor catetelor apare nu doar la nivel numeric, ci şi la nivel geometric al suprafeţelor (figura are o mică greşeală: îi lipseşte o linie în pătratul din stânga, dar sper că se înţelege).
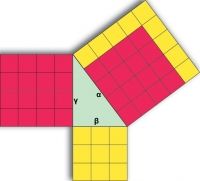
Această imagine sugerează o nouă direcţie de gândire în tema noastră de studiu, anume că dacă unui pătrat (celui roz, cu 16 = 42 unităţi) îi putem adăuga o lărgire cu un rând în ambele direcţii, iar această lărgire (care este reprezentată de un număr impar) este totodată pătrat perfect, atunci obţinem un triplet de numere care respectă Teorema lui Pitagora. Se înţelege? Cam îmbârligat, ştiu. Haideţi să o luăm cătinel.
Suma primelor numere impare este studiată în mod algebric în clasa a X-a, fiind cunoscută în forma: 1 + 3 + 5 + … + (2n – 1) = n2, demonstrată fiind prin inducţie matematică. Există şi situaţii când suma primelor numere impare este inclusă în exerciţii din zona de excelenţă şi olimpiadă la clasele mici gimnaziale, dar subiectul nu este oficial inclus în materie, fiind considerat inaccesibil pentru majoritatea elevilor. Există însă o formă ceva mai accesibilă de a ajunge în zona acestui subiect. Haideţi să o vedem.
Pentru a înţelege ce urmează trebuie însă să schimbăm puţin forma de a privi numerele pătrate. Până acum le-am reprezentat sub forma unor figuri geometrice, anume nişte pătrate împreună interiorul acestora împărţit în pătrăţele ca unităţi de arie. Totuşi în postarea precedentă am avut două imagini care făceau aluzie la o altă abordare.
În primul rând a fost imaginea cu piesele tip “LEGO”, imagine cu pătrate al căror conţinut erau acei “bumbi” specifici, ca nişte buline, aproximante ale unor puncte. Bulinele respective erau ordonate “în pătrat” de trei ori trei ş.a.m.d. Apoi, în imaginea următoare a avut loc o distanţare şi mai puternică faţă de figura pătratului împărţită în pătrăţele. Astfel, în figura cu roşiile aranjate în “formă de pătrat”, figura geometrică numită pătrat a ajuns doar orientativă. “Pătratele” din această imagine nu mai sunt de mult pătrate în sensul geometric, dar totuşi rolul acestora în Teorema lui Pitagora este clar şi evident. Aici roşiile acelea micuţe joacă rolul de buline sau punctuleţe în reprezentarea numerelor pătrate.
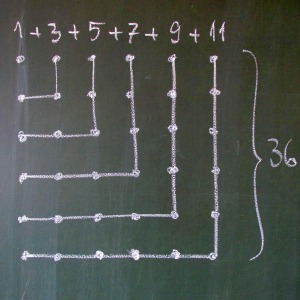
Reprezentarea numerelor prin punctuleţe a apărut în Grecia Antică, învăţaţii din acea vreme folosind pietricele (sau orice altceva, obiecte cât de cât punctiforme, cum ar fi sâmburi) pentru a reprezenta vizual anumite proprietăţi ale numerelor (numerele prime, numerele pătrate sau numerele triunghiulare). Astfel. în diferite lucrări numerele pătrate sau numerele triunghiulare (la fel ca şi altele de inspiraţie geometrică) sunt denumite numere figurate. Faptul că suma primelor n numere impare este egală cu pătratul lui n, de exemplu 1 + 3 + 5 + 7 + 9 + 11 = 36 = 62, poate fi reprezentată prin punctuleţe foarte clar astfel:
Vedeţi în această imagine cum, în afară de 1, orice număr poate fi reprezentat în forma unui “echer de tâmplar” isoscel (nişte L-uri isoscele, numite în antichitate gnomon), însumarea acestora generând o formă de “pătrat”. Astfel, fiecare nou echer, reprezentând un nou număr impar, măreşte pătratul deja existent la următorul număr pătrat. De pildă, dacă la suma 1 + 3 + 5 + 7 + 9 + 11 + 13 = 49 = 72 adunăm următorul număr impar, adică 15, obţinem (1 + 3 + 5 + 7 + 9 + 11 + 13) + 15 = 72 + 15 = 64 = 82.
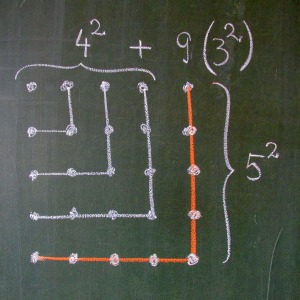
Cu ce ne ajută asta la Teorema lui Pitagora? Păi, aşa-numitul triunghi egiptean, adică suma divină 42 + 32 = 52 se obţine ca 42 + 9 = 52 din următoarea figură:
Asta se întâmplă datorită faptului că 9 este primul număr impar pătrat diferit de 1. Ne punem, pe bună dreptate, întrebarea dacă şi când ne mai întâlnim cu o astfel de situaţie. Păi, desigur la adăugarea gnomonului (a “echerului”) numărului 25, care este următorul număr impar totodată şi pătrat. În acest caz suma numerelor impare până la 23, adică primele 12 impare dă 122 = 144, la care dacă adăugăm 25, obţinem 132 = 169. Avem în acest caz tripletul pitagoreic 122 + 52 = 132. Astfel putem găsi şi alte triplete care îndeplinesc ciudata însumare din Teorema lui Pitagora, următorul fiind de pildă în dreptul numărului impar pătrat 49 (găsirea acestuia elevii o pot primi ca temă opţională).
Se bănuieşte că Pitagora ştia de aceste lucruri, cunoscute de pe vremea civilizaţiei babiloniene. Desigur că Pitagora cunoştea şi obţinerea unor astfel de triplete prin amplificarea celor deja găsite, cum ar fi (6, 8, 10) sau (9, 12, 15) prin amplificare din cel egiptean.. Pe lângă aceste metode există şi alte căi de a găsi triplete pitagoreice, astfel că se găsesc cu totul 11 triplete cu pătratele de cel mult trei cifre (adică până la 1000). Acestea sunt următoarele: (3, 4, 5) şi amplificările sale (6, 8, 10); (9, 12, 15); (12, 16, 20); (15; 20; 25); (18, 24, 30); apoi avem (5, 12, 13) şi amplificarea (10, 24, 26); în final încă trei triplete (7, 24, 25); (8, 15, 17); (20, 21, 29) ale căror amplificări depăşesc însă la pătrat limita de 1000.
Aici v-am arătat calea “babiloneană”de a găsi astfel de triplete, prin figurarea numerelor pătrate, dar şi lista completă până la un anumit nivel de mărime, pentru a le putea folosi în exemple de calcul. Totuşi, eu nu cred că ar trebui să le arătăm elevilor această listă completă. Ei vor trebui să înveţe algoritmul de calcul şi aplicarea acestuia, nu să înveţe pe de rost o serie de rezultate. Astfel, eu la clasă mă concentrez cu elevii mai mult asupra proceselor accesibile de deducere a astfel de triplete şi mai puţin asupra găsirii cât mai multora şi a memorării acestora. Titus şi babiloniile sale
P.S. Vrem – nu vrem, oricum ajungem aici şi la subiectul numit “rădăcina pătrată”: în finalul clasei a VI-a va trebui să le predăm elevilor aplicarea teoremei lui Pitagora dar, prin programă nu avem de studiat până la acel moment finalul calculului, care se face prin rădăcina pătrată (eu am tot căutat-o, dar nu e trecută nici în a V-a, nici în a VI-a). Aşadar, cum să predăm Pitagora fără radicali? Zice nevastă-mea s-o facem ca Pitagora, că nici el n-avea radicalii!!! Logic, nu? Dacă m-ambiţionez, o fac şi aşa, dar nu cred că are sens, pentru că oricum imediat după vacanţa de vară trebuie să le explic cum vine treaba cu rădăcina pătrată. Aşadar, undeva, înainte de lecţia despre Pitagora ar trebui introdusă rădăcina pătrată. Dar cum şi unde?
Cum? Cel mai simplu ar fi de a introduce rădăcina pătrată doar din numerele pătrate, drept operaţie “de probă” a ridicării la pătrat a numerelor naturale. Unde? Cel mai bun loc în materie cred că ar fi fost în capitolul despre numere naturale din semestrul I al clasei a V-a, în continuarea lecţiei despre numere pătrate. Cei care au fost prevăzători, poate chiar au făcut-o acolo, sau o vor face la următoarele clase de a V-a. Dacă însă nu a fost studiată încă rădăcina pătrată, atunci cred că cel mai bine ar fi să o introducem chiar înainte de Teorema lui Pitagora, în ora precedentă. Ca rădăcină doar din numerele pătrate ajunge chiar şi jumătate dintr-o oră. Sunt suficiente doar câteva exerciţii de “extragere” pe baza tablei numerelor pătrate. Pentru asta trebuie însă prezentată tabla numerelor pătrate până la 302 (vezi în acest scop primele exerciţii de pe fişa publicată în postarea http://pentagonia.ro/radacina-patrata-faza-aritmetica-prin-predare-intuitiva/).