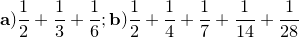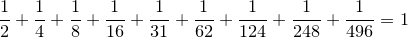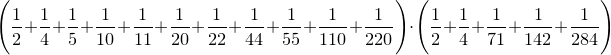Month: February 2016

Ordinea operaţiilor în clasele primare

Prin a 5-a sau a 6-a am surprins-o pe fiică-mea că nu ştia bine ordinea operaţiilor. Făcea mai întâi înmulţirile, apoi adunarile şi apoi scăderile (sau invers, nu mai ţin minte clar) pentru că așa le-a spus doamna învățătoare. La unele exerciţii greşea desigur. Acum, o cunoştinţă a descoperit că fiul ei are şi el probleme cu ordinea operaţiilor. S-a uitat în mai multe manuale şi a găsit că „definiţia” este oarecum incompletă, inexactă, de exemplu:

Într-un exerciţiu în care apar operaţii de adunare, scădere şi înmuţire se rezolvă întâi înmulţirea, apoi adunarea şi scăderea. (Matematică și explorarea mediului, manual pentru clasa a II-a, Didactica Publishing House)

Din definiția aceasta copilul (sau învăţătoarea) poate întelege ce vrea; de exemplu poate înţelege că trebuie făcute mai întâi adunarile şi doar apoi scăderile.

Un singur manual avea o „definiţie” mai corectă, deşi cam greu de înţeles:

  • Înmulţirea este o operaţie de ordinul al doilea.
  • Adunarea este o operaţie de ordinul întâi, deoarece prin adunarea repetată de termeni egali am rezolvat înmulţirea.
  • Scăderea, ca şi adunarea, este o operţie de ordinul întâi.
  • Dacă un exerciţiu conţine una sau mai multe operaţii de ordinul întâi şi de ordinul al doilea, rezolvăm întâi operaţiile de ordinul al doilea, apoi pe cele de ordinul întâi.

(Matematică și explorarea mediului, clasa a II-a, Arthur la Şcoală)

Oare câţi copii (şi învăţători) au înţeles-o greşit şi se miră de ce câteodată nu le iese rezultatul care trebuie, deşi au făcut toate calculele corect?

P.S. Şi dacă tot am ajuns la ordinea operaţiilor în clasele primare, la exerciţii ce cuprind şi diferite straturi de paranteze (să zicem rotunde şi pătrate), oare de ce copiii sunt învăţaţi că după ce rezolvă paranteza rotundă trebuie să o transforme pe cea pătrată în rotundă?

Gaşca cu observaţia

Un exerciţiu de vis

De curând v-am prezentat povestea a două exerciţii frumoase compuse în vacanţa inter-semestrială din februarie 2015 (vezi articolul Aniversarea de 1 an a două exerciţii speciale), explicându-vă cum am ajuns să visez la propriu cel de-al doilea exerciţiu.

Ei, nu cred că trebuie să vă amintesc, de curând am avut iar o vacanţă inter-semestrială, dar decalată cu o săptămână faţă de cea de anul trecut. Şi nu ştiu cum să vă explic, dar iar m-am pus într-o zi la un somnic de după amiază (în 9 feb.). Şi desigur că iar am avut un vis cu un exerciţiu. Acum, totul se întâmpla pe baza faptului că 50 – 1 = 49 (briliant, nu-i aşa?).

După ce m-am trezit am pus la punct detaliile exerciţiului, pe care vă rog să-l savuraţi şi dvs. în continuare (doar exerciţiul a) mi-a apărut în vis; exerciţiul b) este adăugat în stare total trează).

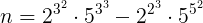1) Fie numărul . a) Arătaţi că 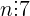; b) stabiliţi ultimele zece cifre ale lui n.

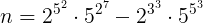În afară de faptul că l-am visat (de data aceasta neforţat), exerciţiul este frumos şi datorită faptului că se pot compune şi altele pe acelaşi calapod, ca temă. De exemplu:

2) Fie numărul . a) Arătaţi că 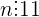; b) stabiliţi ultimele 27 cifre ale lui n.

Reforma uitată (partea a II-a)

Privire asupra psihologiei predării matematicii şcolare

De ce ar trebui să schimbăm forma actuală de învăţământ şi cum ar trebui să o schimbăm, aceasta este tema principală a prezentului. Toată lumea vede aspecte de care este deranjată şi vine cu propuneri de corectări pe măsură pentru mult aşteptata reformă de care se tot vorbeşte.

În partea a doua a eseului Reforma uitată am încercat o analiză a efectelor formei actuale a învăţământului matematic asupra copiilor, plecând de la analiza istorică a reformei din 1980 şi a componentelor acesteia.

Am tratat teme cum ar fi împovărarea materiei şi efectele acesteia, cultul pentru furt, incapacitatea organizatorică pe scară largă, slaba dezvoltare a comportamentului social, cultivarea non-calităţii, slaba dezvoltare a gândirii etc.

În continuare am încercat să dau soluţii pentru găsirea unor căi de reparaţie a acestor defecte întâlnite pe scară largă, căi ce pot fi alese la baza unei reforme sănătoase şi eficiente a predării matematice, reformă ce ar putea fi aplicată şi suportată atât de marea masă a dascălilor, cât şi de marea masă a elevilor români. Totodată am avertizat despre capcana ce ar reprezenta-o încercarea introducerii unor alte modele copiate din diferite ţări. Orice model străin ar trebui mai întâi verificat pe un eşantion românesc. Teoria prezentată se aplică majorităţii materiilor şcolare, având astfel un mare avantaj.

Ideile prezentate nu epuizează subiectul, dar deschid căi nediscutate până în prezent pentru un studiu complet al efectelor predării matematicii în şcoli.

Reforma uitată PII.pdf

Reforma uitată (partea I)

Istoria unei reforme uitate a matematicii şcolare româneşti

Poate a venit vremea să vedem cum s-au petrecut lucrurile la o altă reformă, pe vremea lui Ceauşescu, despre ce a fost vorba în reforma acestuia, impusă profesorilor cu forţa începând de prin 1980. De ce ne-ar interesa acum o reformă petrecută cu peste 35 de ani în urmă? Pentru simplu fapt că trebuie să înţelegem în sfârşit de unde provine actuala paradigmă a învăţământului, de unde provin toate acele apucături ale sistemului pe care actualmente le critică toată lumea.

Impresia personală estă că lumea “nu vede pădurea de atâţia copaci” (o traducere a unei vorbe din germană, preferată de-a profesorului meu de matematică din gimnaziu).

Trebuie să ne aducem aminte ce s-a întâmplat şi să recunoaştem într-un sfârşit cum am fost manevraţi de către Ceauşescu, cum, după un sfert de secol mergem în continuare după cum ne-a programat el. Din acest motiv am intitulat eseul de faţă Reforma uitată.

În studiul realizat am încercat să evidenţiez următoarele aspecte:

  1. Învăţământul matematic din România anilor ’60-’70 a fost unul de foarte bună calitate, având o profundă viziune psihologico-didactică, ce face faţă şi acum unei analize riguroase conform cerinţelor societăţii actuale. Acel învăţământ a fost prezentat magistral în lucrările profesorului Eugen Rusu şi poate fi regăsit în toate manualele şcolare din acei ani. Forme similare de curriculum erau valabile şi la celelalte ştiinţe (desigur cu excepţia istoriei).
  2. Din păcate acel învăţământ a fost înlăturat cu forţa în anii ’80 prin noile manuale şi inspectorii care ajungeau în clase. Degeaba profesorii s-au apărat, până la urmă rând pe rând toţi au cedat, iar cei veniţi noi erau înregimentaţi direct noii linii de predare. Această reformă se sprijinea pe doi piloni:
  3. În primul rând a fost valul de creştere a rigurozităţii în exprimare, a încărcării materiei şi a ordonării acesteia după principiile organizării axiomatice provenită din sistemul universitar. Acest val a devastat ca un adevărat tsunami mai ales geometria gimnazială, responsabilă cu formarea gândirii intuitive la elevi.
  4. Apoi a fost cerinţa din partea conducerii de stat şi de partid de a creşte masiv preocuparea pentru probleme tot mai grele, pentru olimpiade de matematică, ca un mod de dovedire a superiorităţii orânduirii socialiste, în varianta sa mioritică. Această preocupare a prins foarte bine datorită înclinaţiei native a matematicienilor români pentru matematica sportivă.
  5. Din păcate, după înlăturarea lui Ceauşescu nimeni nu a îndrăznit a încerca să corecteze gravele aberaţii ale acelei reforme, astfel încât după o vreme mulţi profesori s-au obişnuit până în măduva oaselor cu acest stil de şcoală, cu această paradigmă. Actualmente nimeni nu mai ştie să vindece această boală, pentru că nimeni nu mai ştie cum arată un învăţământ sănătos. Toată lumea critică învăţământul actual, dar nimeni nu are o alternativă viabilă clară. Eu mă străduiesc de 20 de ani să lucrez în paradigma prezentată de Eugen Rusu în lucrările sale şi pot depune oricând mărturie cât de bine funcţionează la aceşti elevi, la această materie, la aceste examene, la aceste cerinţe.

Reforma uitată PI.pdf

Reforma învăţământului în direct

Pentru prima dată avem posibilitatea să vedem în timp real ce se întâmplă. Lucrurile se petrec cu repeziciune, cum ar spune neamţu’ Hieb auf Hieb, lovitură peste lovitură.

Mass-media şi internetul, în aceste timpuri ce au urmat dezastrului din Colectiv, nu mai iartă nimic, şi bine fac. Fiecare pas al comisiei însărcinată de Dl. Ministru Adrian Curaj cu această nouă reformă este prezentat publicului larg. Şi publicul larg este pentru prima dată în istoria noastră activ în însoţirea acestei reforme. În premieră societatea are posibilitatea să-şi spună cuvântul şi este ascultată.

Pentru prima dată noi, oamenii de rând, avem posibilitatea să intervenim în timp real. De pildă vineri 12 feb. 2016, la Avocatul diavolului de la Europa fm ascultătorii au avut intervenţii deosebite şi emisiunea a trebuit prelungită cu 30 minute.

Pentru prima dată au fost spuse, prin vocea d-lui Cristian Tudor Popescu, adevăruri mari, despre care până acum doar s-a şuşotit în media noastră. Citez un exemplu: Eu am reparat copii stricaţi o viaţă întreagă. Ani în şir cu asta m-am ocupat, cu copii care spuneau “nu ştiu matematică, e greu, nu-mi place”…, copii blocaţi…, au avut un contact greşit, imbecil, din partea profesorului şi s-au scârbit, s-au îndepărtat de matematică. … Această aberaţie numită a preda: copiii stau şi scriu stresaţi, nu înţeleg nimic şi uite-aşa nu reuşesc să intre în contact intim cu matematica..

Săptămâna trecută dl. Moise Guran comentânt despre starea învăţământului la postul tv Digi 24, a luat peste picior autorităţile decidente din învăţământ, clasificându-l în glumă pe Dl. Academician Solomon Marcus drept un extraterestru. Şi într-adevăr aşa este: pentru unii se pare că Solomon Marcus vorbeşte dintr-o altă lume.

Daţi-mi voie să mă coalizez cu dânsul şi să nu mă mai ascund. Da, recunosc în faţa tuturor: şi eu sunt un extraterestru! Da, şi eu predau aşa cum povesteşte dl. Solomon Marcus că ar trebui să facem; da, predau aşa pentru că am avut norocul să înţeleg că trebuie să mă uit mai întâi la elev, la posibilităţile şi la nevoile sale, la elevul de rând, nu numai la vârfuri şi la rigorile unor manuale mult prea pedante. Da, recunosc că mă strădui în fiecare zi să găsesc metode pentru a le prezenta elevilor lecţii cât mai atractive. Da, recunosc, şi eu sunt un profesor dintr-o altă lume.

Titus Grigorovici

16 februarie 2016

Aniversarea de 1 an a două exerciţii speciale

În urmă cu un an, în timpul vacanţei inter-semestriale din februarie 2015, eram preocupat de fracţiile egiptene (vezi Fracțiile la vechii egipteni din octombrie 2015). Un gând nu-mi dădea pace: în timp ce adunam exerciţii pentru temă, cuprinsesem două sume de fracţii unitare, despre care consideram că vechii egipteni nu le-ar fi compus, deoarecă rezultatul acelor sume era de fiecare dată 1. Aceste sume:

sunt construite pe baza numerelor perfecte (desăvârşite) 6 şi 28 cunoscute de către Pitagora (vezi articolul amintit la pag. 3 şi la pag. 5). Cele două sume nu sunt deosebite, dar ridică un mic zâmbet în colţul gurii. În plus, acestea susţin teoria conform căreia Pitagora ar fi aflat de numerele perfecte de la Egipteni.

Ei bine, în acea zi de februarie gândul meu a mers mai departe: dacă aş lua următorul număr perfect, pe 496, ar ieşi un exerciţiu similar, însă mult mai serios, mai greu datorită multitudinii de divizori, iar în urma unei „transpiraţii mult mai serioase” rezultatul ar da tot 1. Or, ştiu din copilărie ce mare bucurie era când la un exerciţiu greu şi complicat obţineam un rezultat frumos. Zis şi făcut, şi iată exerciţiu cu pricina:

Următorul astfel de exerciţiu nu mai poate fi făcut cu acelaşi succes, deoarece 8128 este totuşi prea mare şi calculele sunt de aşteptat a fi dincolo de nivelul de suportabilitate al elevului normal, dar se poate încerca (496 şi 8128 au fost găsite de Nicomah din Alexandria în sec I d.Hr). Oricum, eram bucuros şi încărcat de emoţia realizării unui exerciţiu superb. În această stare, fiind în vacanţă, m-am culcat un pic de dupăamiază, iar în timpul somnului am visat un mega-astfel-de-exerciţiu, adaptând în vis principiul acestor sume la cazul numerelor prietene. Iată ce exerciţiu minunat am visat atunci:

Desigur că şi rezultatul acestuia este tot 1. Cu greu aş putea reda bucuria trăită când m-am trezit şi am luat o coală de hârtie să-l scriu. Desigur că nu am visat toate numerele la rând, ci doar structura: dacă fac aşa şi aşa cu numerele ălea prietene – 220 şi cu 284 – la sfârşit îmi vor ieşi două fracţii inversate, scrise cu cele două numere.

Vă puteţi închipui cum s-au uitat elevii când le-am afişat exerciţiu pe tablă: Ce-aţi făcut dragi elevi în vacanţă? Lăsaţi, nu mă interesează. Să vă spun ce-am făcut eu: am visat un exerciţiu în somn! Uitaţi-l:…. Vă rog să-l rezolvaţi. După ce primii pricepeau că vorbesc serios şi se apucau de lucru, începeau şi restul, iar eu mă plimbam nerăbdător prin clasă. Apoi primii ajungeau la răspuns şi pe rând pe faţa fiecăruia înflorea câte un zâmbet ”de la o ureche la cealaltă”.

În acel moment mi-am adus aminte de o vorbă de-a lui Rudolf Steiner: frumuseţea este umbra spiritului în lumea fizică. Aici se potriveşte cum nu se poate mai bine şi ne dă o explicaţie cum de putem folosi cuvintele frumos şi matematică într-o singură frază.

La Mulţi Ani! celor două exerciţii superbe.

Titus Grigorovici