Fişe de descoperire a matematicii: auto-învăţarea în grupuri mici; matematica – o călătorie de descoperire (Discovery sheets: Self-learning in small groups; Mathematics as a journey to discovery)
În finalul conferinţei d-nei Vestergaard, dânsa şi-a lăsat cca. 5 min. pentrua răspunde la întrebări. Deoarece întrebările erau multe şi se depăşise cu încă 10 min. timpul alocat, dânsa şi-a trecut adresa de e-mail în chat, propunându-ne să-i scriem şi să continuăm discuţiile cu altă ocazie. Mi-am salvat şi eu adresa, i-am scris, şi uite-aşa am ajuns într-o grupă cu alţi şase colegi din Germania, toţi doritori de a afla mai multe despre minunatele ei fişe de lucru şi despre această metodă interesantă. O primă întâlnire, de cunoaştere, a avut loc în 14.04.2021. În grupa respectivă ne-am mai întâlnit până la începutul lui iunie de patru ori (cam la două săptămâni, dar o dată am aşteptat chiar 4 săptămâni, pentru că fusese solicitată pentru o întâlnire online şi de către două doamne profesoare, parcă din Thailanda erau …). Aş dori să vă prezint în cele ce urmează alte aspecte apărute în aceste întâlniri, în plus faţă de cele din timpul conferinţei de la Kassel, sau în accentuarea unora deja exprimate. În această grupă discuţiile au mers în limba germană, aşa încât voi avea mult mai puţine citate în engleză (citatele din explicaţiile d-nai Vestergaard sunt prezentate înclinat).
21.04.2021
Fişele trebuie redactate în paşi mici, pentru ca toţi elevii să se simtă în siguranţă (safe!). Părerea mea este că această politică a paşilor mici ar trebui aplicată în toate formele de predare, mai ales la începutul oricărei teme noi. Un contraexemplu în acest fel ar fi situaţiile despre care am mai vorbit, când unii profesori, în prima lecţie adevărată despre teorema lui Pitagora (în primăvara clasei a 7-a) ajung din prima problemă, cel mult din a doua, deja la situaţii de calcule iraţionale.
Propoziţiile scurte sunt mai accesibile elevilor slabi. În acest sens îmi aduc aminte de o emisiune cu Bear Grills, în care invitatul său, un actor afro-american îl imita pe Obama, spunând că fostul preşedinte al SUA are acest stil de a vorbi în propoziţii scurte (iar asta îi face mesajul accesibil marii mase a populaţiei – comentariul meu).
În mod obişnuit profesorul este poziţionat între elevii buni, pe de-o parte, şi elevii slabi, pe de cealaltă parte. În metoda grupelor mici de lucru, apare o zonă de discuţie directă între elevul bun şi cel slab dintr-o grupă, astfel încât elevii buni ajung să-i ajute direct, pe cei slabi, neintermediat, pentru că profesorul este poate ocupat în altă parte.
Elevii sunt atraşi mai mult de “întrebări”, decât de “ordine”: ce observi dacă compari asta cu cealaltă?, în loc de efectuaţi, calculaţi, găsiţi, demonstraţi!!! D-na Vestergaard recomandă întrebări în loc de cerinţe (Fragen stat Operatoren). Se pare că întrebările sunt percepute ca mult mai blânde, pe când cerinţele apar ca dure, agresive, ultimative. Asta mai ales de către elevii speriaţi de matematică.
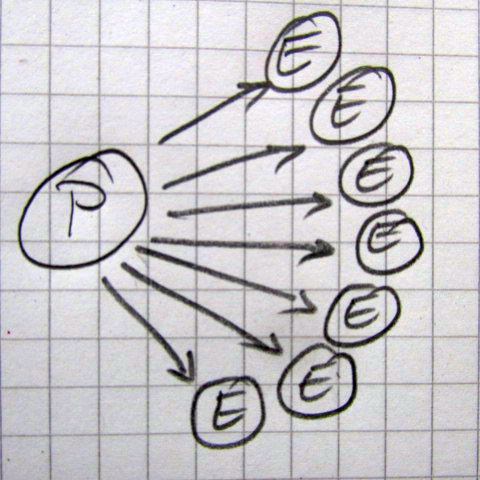
Da, şi destul de repede d-na profesoară a ajuns iar la subiectul ei preferat, anume la nivelul de siguranţă al orei de matematică, din punct de vedere al elevului speriat (the level of safety!). Aici ne-a adus o nouă schiţă reprezentând istoricul de experienţe al elevului obişnuit:
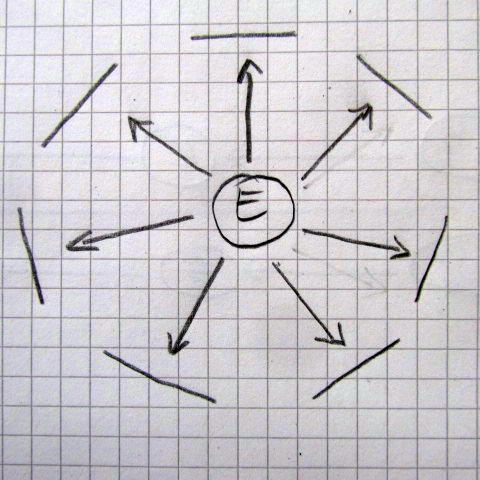
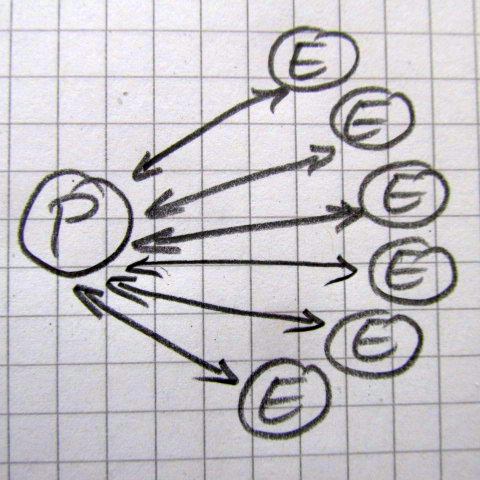
Astfel, în viaţa lor şcolară, multor elevi le sunt blocate iniţiativele, pe baza diferitelor argumente: asta nu e voie, asta nu se face, e interzis!, e greşit, Ha-Ha! (adică s-a râs de el) etc. În schiţa de mai sus elevul este prezentat în centru, săgeţile reprezintă iniţiativele sale (inclusiv răspunsurile sale), iar liniuţele care blochează diferitele săgeţi reprezintă argumente de refuz de tipul celor enumerate aici. În urma multor astfel de experienţe, de la o vreme elevul se blochează, nu mai are iniţiative, apărând un fel de prăbuşire în sine. Pentru un elev care-şi expune părerea cu entuziasmul plin de inconştienţă al vârstei, aceste argumente de blocare acţionează înjositor, mai ales dacă se întâmplă în faţa clasei (socialul este de multe ori vital pentru copii, mai ales în pubertate). În filmuleţele prezentate în timpul conferinţei diferiţi elevi povestiseră despre înjosirile repetate prin care trecuseră în trecut (adică în perioada cunoscută la noi drept “gimnaziu”).
Este foarte important ca elevul să nu fie înjosit de nimeni, niciodată! (Niemals gedehmütigt werden von niemanden) Dacă s-a râs de un elev, de exemplu dacă acesta a întrebat pentru că n-a înţeles, atunci acesta nu va mai întreba niciodată. Mai mult, nici ceilalţi din clasă nu vor mai îndrăzni să întrebe, din frică de a nu fi şi ei înjosiţi (în general se subânţelegea înjosirea din partea unor colegi mai buni, nu din partea profesorului).
Profesorul trebuie să trezească din nou curajul – în matematică – şi la elevii mediocri sau chiar submediocri. Idealul cel mai înalt al unui profesor trebuie să fie de a explica aşa de bine, încât să înţeleagă toţi elevii.
Cât despre elevi, în cazul în care unul nu a înţeles, acesta are responsabilitatea de a întreba pe cineva pentru a se lămurii (fie pe profesor, fie pe un coleg). Dacă un elev n-a înţeles, acesta trebuie să se mai străduiască până înţelege (este dator să se străduiască).
Dar pentru asta, elevul trebuie să se simtă în siguranţă (safety): elevul poate să vină în această oră de matematică cu tot ce este el (desigur, în limitele bunilui simţ). Spunea d-na profesoară: dacă observ o înjosire între elevi, atunci acţionez imediat împotriva vinovatului. Pentru dânsa înjosirea elevilor slabi de către cei buni, chiar şi cea neintenţionată, inconştientă, reprezintă una din grijile majore, pentru că este cauza principală a blocajului celor inhibaţi. Elevul bun trebuie să-şi dezvolte un simţ social pentru “cel de alături”, de a nu-l înjosi nici din greşeală, darămite intenţionat. Chiar şi într-o şcoală care nu promovează pe faţă excelenţa (cum este a noastră: “să văd care ştie primul”), apare natural o concurenţă între elevi, bazată pe cursa după admiraţia dascălului sau pur şi simplu bazată pe bucuria de a fi găsit răspunsul corect. Dimpotrivă, este o artă felul cum îi spui unui elev care a dat un răspuns greşit că nu e bine. Este normal ca celalţi elevi să nu stăpânească această artă şi de aici apare fenomenul respectiv de înjosire a celor slabi (la noi nici profesorii nu-şi prea fac gânduri despre ideea de a nu-i înjosi pe cei care nu au nimerit răspunsul corect; iar “datoria” de a da note, inclusiv slabe, doar exacerbează de multe ori acest fenomen).
Spune dânsa că profesorul (mai ales cel de matematică) trebuie să fie un garant al siguranţei celor mai slabi (the spaceholder for safety). Trebuie să ne străduim să facem o atmosferă “safe”, o atmosferă în care orice elev să se simtă în siguranţă. Eu, ca profesor, trebuie să le pot arăta elevilor că păstrez acest spaţiu “safe”, că păstrez acest “spaţiu al orei de matematică” într-un nivel de siguranţă bună, de a nu fi înjosit, pentru orice elev.
Aici iau o pauză din traducere, pentru că mă năpădesc amintirile unei întâmplări cu aproape zece ani în urmă. Era vorba despre o cerere de transfer la şcoala noastră (începutul clasei a 8-a) din partea unei mame a cărei fiică era în mod agresiv înjosită de profesoara de matematică de la liceul de renume de unde vroiau cu disperare să plece. Când un elev nu ştia, profesoara îl ţinea în picioare şi îi punea pe toţi ceilalţi să rădă de respectivul ghinionist. Pentru că nu prea se ridica la pretenţiile elitiste ale acelei profesoare, eleva cu pricina ajunsese într-un blocaj total datorită acestor tratamente repetate. Cum se spune, era “pe marginea prăpastiei”. Atunci când mama m-a prezentat elevei respective, “dânsul este domnul director, cu dânsul vei face matematică”, fata a izbicnit instantaneu în plâns. Ulterior dânsa mi-a spus că a făcut gestul respectiv intenţionat ca să văd cât de gravă este situaţia.
Am primit-o în şcoala noastră şi i-am spus că îi las timp până la vacanţa de iarnă; nu o voi asculta, nu o voi întreba, singura interacţiune matematică va fi doar când va considera ea să zică, sperând că astfel i se vor vindeca rănile de pe sufleţel. Înainte de Crăciun i-am adus aminte de înţelegere, mi-a zis că e OK, iar din ianuarie a fost elevă cu drepturi şi datorii egale cu ceilalţi. A avut noroc de un an cu subiecte la EN mai uşoare (foarte mulţi au luat 10 în acea vară, inclusiv o elevă din clasa respectivă), iar ea a reuşit undeva peste 6. Dacă am fi avut măcar un semestru în plus, sunt sigur că s-ar fi apropiat chiar de 8.
Citind notiţele după care vă scriu aceste rânduri, nu pot să nu fiu uimit de diferenţa de la cer la pământ între situaţia respectivă şi atitudinea descrisă de colega din Norvegia. Din acest motiv am scris la sfârşitul primei părţi a acestei prezentări, că bănuiesc că situaţia prezentată s-ar putea să pară multora de-a dreptul extraterestră. Dar să revenim la d-na Vestergaard.
Pentru dânsa este vorba despre arta de a reuşi să-i faci pe elevi să iasă din cochilia lor. Dânsa a folosit expresia să reuşeşti să îndepărtezi această “capsulare”, fiecare elev închizându-se în capsula sa (diese Abkapseln wegkriegen, jeder in seine Kapsel). Spune dânsa: aş dori să le “însuşeşc” în mod drag matematica acestei clase (ich möchte liebevoll die Mathematik dieser Klasse eineignen).
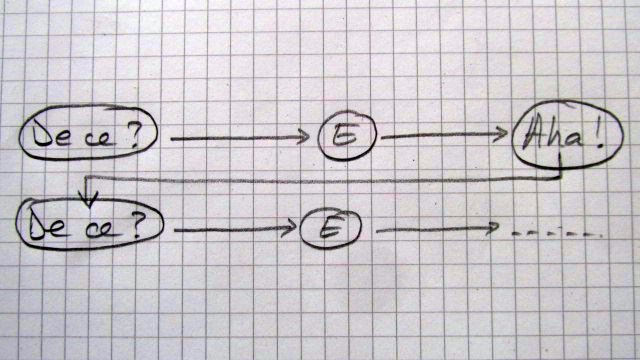
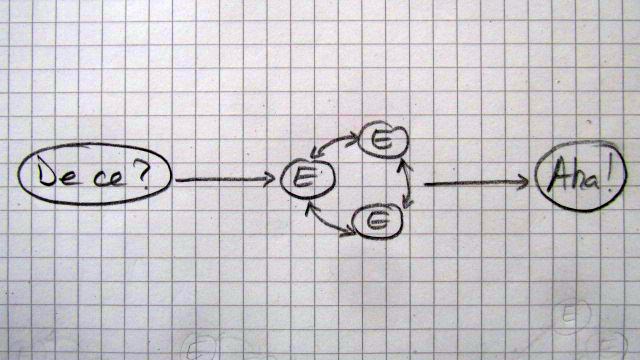
În altă ordine de idei, dânsa spunea că procesul de descoperire (a elementelor lecţiei, desigur) acţionează altfel decât explicaţiile, la care de multe ori elevul nu are nici un chef să fie atent. La desoperirea unui lucru ai o mare bucurie, pentru că primeşti o doză de dopamină (Dopamin-shott), dar asta nu se întâmplă dacă treaba respectivă îţi este explicată. Problema este că noi profesorii trebuie în aşa fel să pregătim materialul, încât elevii să descopere singuri, să le vină singuri ideea despre ce şi cum. Apoi, cu timpul, elevul va avea încredere că noi îi pregătim materiale la care, dacă se porneşte să lucreze, va ajunge să descopere anumite lucruri, iar aceasta îi va da o mare bucurie (doza de dopamină), asta poate chiar de mai multe ori într-o lecţie (lectia ca un spaţiu temporal pentru căutare de comori, de “nestemate matematice”, aducătoare de mare bucurie; ce frumos spusese în timpul conferinţei “vânătoare de comori”).
Dar pentru început trebuie să ne străduim ca elevii să fie absobiţi în acest vârtej. Dacă o grupă nu începe să lucreze, trebuie să-i atragi cumva în acest proces, în vârtejul curiozităţii, care duce apoi la descoperire. Această ultimă precizare a venit în urma unei întrebări: dar ce facem dacă elevii dintr-o grupă nu încep să lucreze? Răspunsul doamnei profesoare a fost mai amplu, dânsa explicând cum încearcă să-i convingă prieteneşte, în nici un caz agresiv (precizarea cu agresivitatea îmi aparţine).
Mai trebuie să fac aici o observaţie: dânsa foloseşte cuvântul descoperire în sensul folosit şi de George Pólya în cartea sa Descoperirea în Matematică, respectiv descoperirea unei rezolvări sau a altor elemente matematice, care desigur au fost pregătite dinainte şi ascunse pe acest traseu al “căutării de comori”, care reprezintă fişa de lucru, sau orice altă sarcină dată de către profesor. Deci, fiecare elev trebuie să descopere lucrurile respective din nou. Aşa este mai bine, aşa îi va aduce bucurie (doza de dopamină), aşa va ajunge să iubească matematica, nu explicândui toate cele şi cerându-i să le recepţioneze în mod pasiv. Eu personal am experienţă multă în a-i îndruma pe elevi frontal pe această cale a descoperirii elementelor unei lecţii (predarea prin descoperire, ca formă extremă a predării prin problematizare). Ar mai trebui să reuşesc pasul către redactarea unor fişe în acest sens.
Revenind la sfaturile d-nei profesoare, dânsa preciza că – cel puţin pentru început şi mai ales pentru elevii mai slabi – profesorul este responsabil atât pentru alegerea unor teme cât mai entuziasmante în sine (unele teme sunt mai potrivite, altele sunt “mai plate” din acest punct de vedere), cât şi mai ales pentru entuziasmarea elevilor, elevii mai slabi nefiind în stare la început să se entuziasmeze pentru o temă nouă din matematică. Iar dacă nu este entuziasm, atunci elevii nu au nici imboldul de a lucra singuri pe aceste fişe.
5.05.2021
În această nouă întâlnire d-na Birte Vestergaard a atenţionat cum frica de matematică este combătută prin experienţe de succes în matematică. Apoi dânsa preciza că orice metodă se numeşte cu adevărat “pedagogică”, durează mult mai mult, mult-mult mai mult decât doar predarea simplă a materiei respective (prelegerea este cea mai eficientă cale din punct de vedere temporal, dar este şi cea mai puţin pedagogică)
Mai ales la începutul unei teme noi este foarte important să ai răbdare, să le dai elevilor timp să intre în noua temă şi să se acomodeze în aceasta. După ce s-au stabilizat în subiectul cu pricina, la o adică, dacă spre sfârşitul orei îţi dai seama că nu-ţi mai ajunge timpul în ritmul acesta lent, atunci poţi să-ţi permiţi şi o porţie de predare, pentru că elevii te vor putea urmării (au înţeles despre ce este vorba; sunt obişnuiţi deja să gândească în acest subiect). Dar oricum, nu-i foarte sănătos (să predai prin prelegere).
Ideea este deosebit de bună: la început mergi cu răbdare, astfel încât toţi elevii să prindă subiectul respectiv, cu nuanţele sale, iar apoi, la nevoie, poţi şi să măreşti viteza spre final. Cu alte cuvinte, preciza Birte (ne cam tutuim): timpul “pierdut” la început ca să prindă toţi, se câştigă mai încolo.
Ca exemplu – pentru entuziasmarea elevilor şi atragerea lor în acel vârtej al curiozităţii şi al lucratului – ne-a dat introducerea progresiei geometrice pe baza vechii probleme cu boabele pe tabla de şah, cum construieşte generalizări, iar în final scoate (ca o bagatelă) observaţia plină de uimire: UAU, există şi progresii aritmetice!
Revenind la problema cu boabele de orez pe tabla de şah, dânsa ne-a recomandat filmuleţul existent pe Youtube sub numele Ricecornparable German/English, uşor de găsit direct si la adresa https://www.youtube.com/watch?v=KnQZ3Mg6upg. Poate fi folosit şi la clasă, dar mai ales în online (merge desigur dat şi ca temă, pur şi simplu să se uite la filmuleţ acasă cu scopul evident de continuare a stării de entuziasmare).
Despre prezentarea de final au fost câteva observaţii deosebit de valoroase. Astfel, prin această activitate zilnică elevii sunt educaţi să prezinte un material, să nu se lungească (adică să respecte timpul celorlalţi, “ai 5 minute”), să fie clari în prezentare. Elevii care ascultă trebuie să fie atenţi, dar să fie şi empatici: dacă au o nelămurire, trebuie să înveţe cum să o spună fără a-l jigni pe cel de la tablă, care este desigur într-o poziţie vulnerabilă. Empatia este exersată şi de cel care prezintă: el trebuie să o facă simţindu-şi toţi colegii, astfel încât şi cei mai slabi să înţeleagă. În pregătirea scurtă a prezentării, elevii se antrenează ca să ajungă la esenţa unui material (să nu “bată câmpii”).
Dacă au de ales, elevii vor la tablă doar dacă ştiu că vor avea succes. În acest format de lecţie elevii sunt chemaţi la tablă pe un material pentru care tocmai s-au preocupat (proaspăt) şi pe care tocmai au avut timp să îl pregătească (a fost avertizat din timp). Oricum, aceste prezentări ale elevilor sunt un element greu de introdus iar acest pas trebuie făcut cu multă răbdare.
La început, în primele ore lucrate pe acest format, grupa aleasă să facă prezentarea primeşte timp până a doua zi: “o faceţi azi într-o pauză sau când aveţi puţin timp liber”. Cu cât elevii capătă mai multă experienţă (poate după un an), procesul poate fi grăbit. Ei sunt anunţaţi că au fost aleşi să facă prezentarea, au pentru asta 2-3 minute la dispoziţie, iar apoi vin direct la tablă să facă prezentarea (D-na profesoară mima o încurajare de tipul: “puteţi s-o faceţi, aşa-i?, eu sunt sigură că puteţi!“). Probabil că o corelare între o temă mai accesibilă şi o grupă care a terminat mai repede poate fi numai bună pentru a trece la această fază mai matură. Cu timpul reuşesc apoi toţi să treacă la prezentări fără o mare pregătire.
O astfel de activitate desfăşurată cu succes îi dă foarte multă încredere matematică unui elev, pentru că de obicei în prezentarea sa acesta a fost nevoit să includă noţiuni descoperite de el în acea oră. În general îl antrenează şi îi dă încredere să cuprindă corect orice subiect nou.
2.06.2021
De la început s-a pus problema în această grupă de preluare a unor fişe de descoperire. D-na Vestergaard le-a oferit cu drag, doar că aceste erau în norvegiană. Dânsa fiind însă daneză, se pare că au funcţionat mai bine programele de traducere din daneză (nu ştiu care sunt diferenţele sau asemănările dintre cele două limbi). Oricum, de la o vreme au apărut în grup fişe în limba germană. Eu nu le pot folosi ca întreg pentru că forma noastră de matematică este mult diferită de cea practicată acolo. Pot doar să mă inspir şi eventual să iau pasaje din acestea pentru a le integra în viitoare fişe de lucru redactate aici.
La această întâlnire unii dintre colegi acumulaseră deja experienţă la clasă pe aceste fişe, aşa încât apăreau şi întrebări ţintite. Simt că una dintre aceste întrebări ar fi de mare interes pentru profesorul român: ce se întâmplă cu elevii buni, care termină repede iar apoi se plictisesc (de pildă dacă o grupă termină mult înainte)? Nu poţi să-i tot ţi în urmă, doar să le explice celor mai slabi. Mai ales în cazul temelor de lucru mai uşoare, pentru astfel de cazuri d-na profesoară vorbea de nişte fişe suplimentare, tratând ramuri ale temei zilei, aspecte ce nu au fost incluse în fişa dată tuturor. Aceşti elevi au apoi ca sarcină în final să le prezinte pe scurt şi colegilor.
Revenind la clasa întreagă, mi-am notat un citat care merită evocat: bine introduşi şi conduşi într-un spaţiu lipsit de frică (vorbea de activitatea profesorului de conducere a elevilor prin lecţia de matematică). Acest tip de lecţie face diferenţa între învăţarea pasivă şi învăţarea activă, dar asta funcţionează doar într-un spaţiu sigur (in a safe room). Legătura este foarte importantă: în siguranţă dacă întrebi, în siguranţă dacă greşeşti, în siguranţă să-ţi aduci ideile tale.
D-na Vestergaard spunea că acest format de lecţie transformă “vântul din faţă” în “vânt din spate”. Elevul slab ajunge să trăiască zilnic bucurii de felul: Uau! EU am înţeles asta! Elevul bun are zilnic bucurii de felul: Uau! EU am descoperit asta! Dar pentru asta profesorul trebuie să reuşească să transforme cultura de predare, să-şi întoarcă paradigma de gândire dinspre sine, ca sursă de matematică, înspre elev, ca obiectiv principal al lecţiei. Şi, după cum am văzut în aceste întâlniri, cultura educaţională a profesorului trebuie să se îndrepte către elevi în general (nu doar către cei buni la matematică) şi totodată trebuie să se îndrepte către elevul întreg, nu doar către gândirea şi stocarea matematicii de către elevi.
O ultimă observaţie personală aş avea aici. În timp ce lucrez la acest articol, în mass media lumea este năucită de atâtea ştiri despre accidentele de pe şoselele din România. Vara aceasta, finalul lunii iulie şi începutul lui august au adus foarte multe accidente pe şosele, soldate din păcate cu multe victime. De peste tot se cere “să ne respectăm unii pe alţii în trafic!”. Dar de ce avem această situaţia destul de generalizată? Păi simplu, după 40 de ani în care în şcoli s-a promovat doar concurenţa şi egocentrismul, acesta este rezultatul. Cum să ne respectăm unii pe ceilalţi când numai asta nu am învăţat în timpul şcolii?
Dacă ne putem aştepta ca foştii elevi buni să nu ajungă nişte adulţi frustraţi (pentru că au primit de obicei factorul formator al matematicii) dimpotrivă, în cazul foştilor elevi slabi, înjosiţi şi frustraţi masiv în anii de şcoală, efectul este debordant: odată ajunşi adulţi, la volanul unor maşini puternice, “păzea! că vine el!”. Primul pas pe acest “drum al revanşării” sunt desigur câinii de luptă” din diferitele rase care impun frică (toată lumea se dă de-o parte când îi iese în cale un Rottweiler sau un Pitbull). Acest pas apare de obicei mai repede, înaintea vârstei de 18 ani. Apoi apare dorinţa fierbinte pentru carnetul de conducere şi pentru o maşină cât mai “tare”.
Tabloul este desigur mult mai complicat de atât, dar oricum eu văd multe conexiuni cu cele prezentate mai sus. Dau aici câteva exemple la întâmplare: educarea empatiei faţă de ceilalţi, capacitatea de planificare (aplicată de pildă pe planificare drumului către mare), educarea pentru a nu epata, o perioadă şcolară (de formare) care să nu producă o viitoare personalitate frustrată etc. Iar acestea ar fi doar câteva aspecte la care noi profesorii, formatorii de viitori adulţi, ar trebui să ne gândim.
Iar acum voi fi deosebit de dur: când un şofer este atât de inconştient în comportamentul său pe şosele, încât ajunge să omoare oameni (poate inclusiv pe el însuşi sau din familia sa), atunci câtă vină ar trebui să resimtă foştii săi profesori care s-au ocupat ani în şir la orele de matematică doar înspre doparea celor buni ai clasei (pe baza cărora să-şi poată apoi etala rezultate la concursuri şi examene), neglijându-i pe cei slabi, înjosindu-i cât de des, astfel încât mulţi dintre aceştia să ajungă adulţi frustraţi, care n-au beneficiat în nici un fel de factorul educativ general al matematicii, având dimpotrivă o personalitate distrusă şi agresivă??? CTG (va urma!)