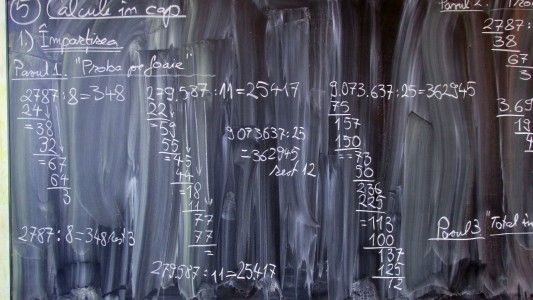Anul 1981 marca ultima apariţie editorială pentru profesorul emerit Abraham Hollinger. Manualele sale se pierd în negura timpului (avem unul chiar şi din perioada interbelică). A fost un metodist de excepţie, fiind acceptat ca autor şi în perioada comunismului sovietic. Pentru foarte mulţi Hollinger contează ca autor al manualelor de geometrie pentru clasele gimnaziale în anii ’60-’70. În 1981 manualele sale erau înlocuite cu unele pe o linie nouă, adaptată noilor “vremuri şi cerinţe”. Cumva însă a fost lăsat să mai “scrie” o culegere de probleme de geometrie, oarecum “testamentul său matematic”. Citez din prefaţa acestei cărţi:
Dacă la aritmetică şi algebră elevul mijlociu (!) îşi însuşeşte cel puţin un minim de cunoştinţe şi este capabil să le aplice, sînt foarte mulţi elevi care nu se aleg aproape cu nimic din tot ce li se predă la geometrie. Este adevărat că există o deosebire esenţială între formele de activitate care se cer elevilor la aceste două părţi ale matematicii: la prima predomină aspectul algoritmic, iar la a două raţionamentul. Totuşi consider că această inegalitate a rezultatelor se datoreşte şi modului de predare. La aritmetică şi algebră, ca elevul să-şi însuşească un lucru oarecare, el este pus să-l repete de foarte multe ori. De exemplu, ca să înveţe regula de trei simplă, elevul este pus să rezolve multe probleme care diferă doar prin semnificaţia concretă a numerelor; ca să înveţe să ridice un binom la pătrat, nu i se dă numai formula pentru (a + b)2, ci el este pus să facă multe exerciţii ca (2x + 1)2, (3a – 2b)2 etc. La geometrie, însă, după ce i se predă o teoremă sau un grup de teoreme, se trece imediat la probleme complexe în care elevul regăseşte cu greu situaţia simplă, schematică a figurii care s-a folosit atunci cînd s-a predat teorema respectivă. Ideea despre care am spus m-a determinat să alcătuiesc aceste Exerciţii este de a folosi în predarea geometriei o metodă asemănătoare cu cea folosită în aritmetică şi algebră, şi anume de a propune elevilor numeroase exerciţii simple, chiar foarte simple în comparaţie cu cele uzuale. Prin aceasta elevul se obişnuieşte treptat cu diferitele situaţii şi urcă în pantă lină la problemele complexe. Astfel de exerciţii nu prea există în cărţile pe care le cunosc; le-am compus. (…) (A. Hollinger, Probleme de geometrie pentru clasele VI-VIII, Ed. Didactică şi Pedagogică, 1982; din Prefaţă, pag. 3).
Am citit de multe ori acest pasaj ce m-a impresionat. Există marile probleme ale geometriei, dar pentru a putea porni primii paşi în geometrie, elevii au nevoie de nişte aşa-zise “probleme” care să le fie accesibile, simple şi totuşi să le pună mintea în mişcare. Astfel de probleme nu existau, aşa încât dânsul a început să le compună. Putem să vedem aceste probleme ca pregătitoare pentru adevăratele probleme de geometrie. Culegerile lui Grigore Gheba aveau probleme de geometrie din acelea grele, complexe; cele ale lui Hollinger erau mai “pentru începători”. Acestea se regăsesc oricum şi în manualele pentru clasele VI-VIII din anii ’60-’70. De fapt Holiinger compusese aceste probleme pentru manuale, adică pentru elevul “mijlociu” (vă sună cunoscut, apropos de corpul central al Clopotului lui Gauss?).
Cum am mai zis, am citit de multe ori acest pasaj, iar cu timpul ideea a început să lucreze în mintea mea, generând în acest sens o nouă normalitate: este normal să fii atent la evoluţia elevilor şi la nevoile lor (mai ales a elevului “mijlociu”), iar dacă observi că învăţarea merge greu, atunci este normal să inserezi exerciţii sau paşi noi de predare (desigur mai mici) pentru pregătirea lecţiilor de bază.
Ce doresc eu să vă prezint acum nu este însă rezultatul unui proces conştient de imitare a lui Hollinger, ci mai degrabă o analiză ulterioară a drumului de generare a unei noi lecţii, cu exerciţiile aferente. Fără să-mi dau seama am făcut acelaşi lucru ca dânsul: văzând că lucrurile merg tare greu, am încercat să înteleg de ce, iar apoi am început să generez exerciţii pregătitoare (ordonate într-o lecţie, că aşa dă bine) pentru pregătirea unui pas necesar la o lecţie oficială. Despre ce este vorba?
În semestrul I din clasa a 5-a elevii învaţă să descompună numerele naturale în factori primi. Metoda folosită este cea “cu bară”, cunoscută de toată lumea şi considerată de toţi drept o banalitate. O fi aceasta o banalitate, doar că mulţi elevi (părerea mea că peste 50-70% din populaţia şcolară) nu o înţeleg din prima. Unii o mai înţeleg în perioada următoare, dar rămân oricum o parte importantă care apucă să o înţeleagă doar dacă îi ajută cineva (un membru al familiei sau un profesor angajat particular). Ultimii “mohicani” o înţeleg de-abia prin clasa a 7-a când se dumiresc, odată cu scoaterea factorilor de sub radical. Dar, de ce este atât de grea descompunerea pentru mulţi elevi? Simplu: aceasta se bazează pe împărţirea ce se cere automat făcută în cap (la numere mici, cele prime, cum ar fi 2, 3, 5, cel mult la 7 sau 11). Până în acel moment însă, nimeni nu le-a cerut elevilor să înveţe şi să-şi exerseze împărţirea în cap. Toţi ştiu să facă împărţiri scrise (chiar la numere mai mari), dar acum trebuie să le facă în cap şi asta repede (că n-avem timp de pierdut, să tot exersăm!). Bănuiesc că unii profesori nici măcar în timp ce-i învaţă descompunerea nu le atrag atenţia că ei, elevii, trebuie acolo să facă mai multe împărţiri în cap, toate într-o succesiune în cascadă la o singură descompunere.
Eu sigur nu am pretenţia să fiu atât de deştept încât să-mi fi dat seama că aici este nevoie de inserarea unui pas intermediar, dar “zeii matematicii” m-au ajutat şi mi-au trimis o sursă de inspiraţie: în urmă cu cca. 15 ani m-am ocupat o vreme cu un băieţel de a 6-a a cărui familie se mutase de la Vienna. La un moment dat am observat la acesta un mod ciudat de a face împărţirile; mi-a spus că aşa le învăţase în clasa a 5-a în Austria. Le-am reluat, le-am înţeles şi am văzut că acestea erau o modalitate de împărţire într-o formă intermediară între algoritmul complet şi împărţirea integral în cap.
Am început să le-o arăt elevilor ocazional, iar cu timpul s-a cristalizat o lecţie. Pentru ca descompunerea numerelor să meargă “şnur” era bine să inserez înainte, de pildă în perioada de recapitulare de la începutul clasei a 5-a, această nouă metodă, cât şi ulterior cerinţa de a ajunge să facem împărţiri în cap.
Este evident că toţi elevii ce parcurg exerciţiile din acest pas intermediar pot apoi să treacă uşor la împărţirile în cap. Iar, ulterior, când vine descompunerea numerelor în factori, toţi elevii care au învăţat împărţirile în cap, toţi aceştia vor înţelege din prima şi descompunerea. Este atât de simplu!
Concret, am generat o lecţie (ce se poate întinde lejer pe 2 ore), compusă din trei părţi. Partea întâi reprezintă o recapitulare simplă a algoritmului de impărţire scrisă. Fac aici o mică “paranteză”: pentru exersarea şi fixarea rapidă de către cât mai mulţi elevi a algoritmului împărţirii, eu consider că elevii trebuie să primească să exerseze situaţii cu deîmpărţit mai lung (pentru repetarea “algoritmică”), dar cu împărţitor relativ mic. Anume, pentru împărţitori trebuie alese numere cât mai mari, dar cu “tabla înmulţirii” accesibilă (cu şirul de multiplii lesne), cum ar fi de o cifră mai mare (7, 8, 9) sau de două cifre (11, 12, 15, 20; 25), eventual asimilabile cu acestea (tabla înmulţirii cu 24 are elementele puţin mai mici decât cea cu 25). Ar mai merge eventual împărţiri la 111 (dar nu ştiu care este câştigul); obiectivul nostru este ca elevii să ajungă să poată împărţi în cap la 2, 3, 5, cel mult 7 sau 11.
Partea a doua aduce împărţirea din Austria, pe care o denumesc la clasă “cu proba în cap” (aici denumesc totodată şi partea întâi ca împărţire “cu proba scrisă”). Apoi vine partea a treia, denumită simplu “împărţirea în cap”. Poza de mai sus (pe o tablă foarte curată) conţine pe scurt doar paşii noi pentru dvs. Mai am un set de poze, cu toţi cei trei paşi, dar pe o tablă execrabilă. Pentru înţelegere de ansamblu mai bună merită însă să le prezint şi pe acestea.
Pentru cei doritori de mai mult, lecţia poate primi şi o prelungire, anume înmulţirea în cap cu numerele 5; 2 sau 25 (care de fapt reprezintă o aplicaţie a împărţirii în cap la 2; 5 respectiv 4, cu ataşarea în final a unui zero, sau a doi de zero). Şmecheriile întotdeauna le plac elevilor şi îi atrag.
Pentru cei doritori ataşez în final şi fişa de lucru aferentă acestei lecţii. Este facută astfel încât să o imprimaţi pe ambele feţe, apoi să o tăiaţi în două, iar elevii să primească o fişă faţă-verso în format A5 (făcând astfel economie la hârtie). CTG
P.S. Putem considera cele de mai sus ca un prim exemplu. În contextul celor spuse de prof. Hollinger, cu timpul am mai generat paşi pregătitori şi la alte lecţii, cum ar fi de pildă fractiunile ca pregătire a studiului fracţiilor ordinare, dar despre asta cu o altă ocazie.