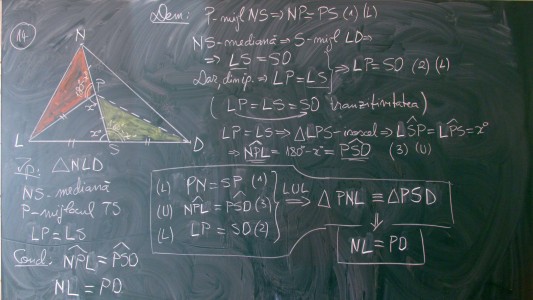Category: Editoriale

De multă vreme societatea românească “de dreapta” este divizată între cei ce susţin un adevăr vizibil “ca lumina zilei” şi cei care îl contestă. În tot acest timp lipsea dovada palpabilă, demonstraţia fără de tăgadă, deşi în urma evenimentelor din ultimele săptămâni situaţia părea tot mai clară. Iată însă că zilele acestea am reuşit să demonstrez matematic, fără dubii, prin metoda triunghiurilor congruente, ceea ce mulţi simţeau de ani buni. Citeşte cu atenţie demonstraţia din problema următoare şi vei înţelege TOTUL despre ce ni se întâmplă! (Erată în poză: Ip. rândul 3: P mijlocul NS în loc de TS)

Domnul Cristian Tudor Popescu nu ratează nici cea mai mică ocazie de a insera în luările dânsului de cuvânt comentarii despre matematică. Probabil că este o metodă prin care îi râcâie pe toţi acei inculţi ajunşi “sus” şi dând cu părerea cu părerea în dreapta şi în stânga în mod cât mai “pretenţios”. Am spus “inculţi”, lăsând descrierea la general, fără a accentua “inculţi matematic” pentru că o persoană cu adevărat cultă în alt domeniu nu are probleme atunci când se vorbeşte de matematică. Inculţii cu adevărat au însă o frustrare profundă legată de matematică: această disciplină i-a chinuit cu adevărat în şcoală şi pentru asta nu o suportă.

Am putut observa şi eu acest fenomen în anii când umblam prin ţară ca reprezentant al sistemului Waldorf, încercând să-i conving pe tot felul de inspectori din alte judeţe că această şcoală nu este o alternativă educaţională pentru copii cu dificultăţi de învăţare. De fiecare dată când aveam ocazia – în discursurile mele – o luam “creanga” prin matematica de liceu ca să le dovedesc că se face treabă şi în această şcoală. Astfel, la primul “logaritm” sau “cosinus” primeam o reacţie de genul “am înţeles, ok, dar puteţi să ne scutiţi de acestea“,

Revenind la comentariile d-lui CTP, pe baza experienţei din alte ocazii, când m-am trezit că după o vreme înregistrările respective dispăreau de la adresele memorate, am decis ca de data asta să preiau textul complet, fără a avea mare lucru de completat. Iată transcris întregul comentariu al D-lui Cristian Tudor Popescu, difuzat joi 30 martie 2023 la postul Europa FM în rubrica Judecata de Joi, din cadrul emisiunii Deşteptarea.

*

N-aş fi crezut că fake-news poate pătrunde şi în matematică. Din când în când mai rezolv probleme, în special de geometrie, ca să am impresia că respir aer curat după duhorile emanate de politică şi presă, pe care le inhalez cotidian.

Pe nu-ştiu-câte site-uri s-a ivit ştirea că două liceene din America au demonstrat trigonometric teorema lui Pitagora şi că au folosit “legea sinusurilor”. Nimeni nu publică demonstraţia respectivă, “s-o văz şi eu”. Nici o autoritate matematică nu a verificat-o şi nu i-a dat certificat de valabilitate. Totuşi, se titrează în neştire: Teorema lui Pitagora demonstrată după 2000 de ani. În realitate sunt vreo 2500, şi de atunci a fost demonstrată în peste 300 de moduri.

O asemenea demonstraţie – trigonometrică – este înainte de matematică imposibilă logic. S-a folosit în demonstraţie “legea sinusurilor”? Păi, de cum ai rostit sau ai scris sinus, asta presupune – dat fiind că sinusul e raportul dintre cateta opusă unghiului şi ipotenuză – un triunghi dreptunghic, în care este valabilă teorema lui Pitagora.

În logică această greşeală se numeşte petitio principii, anticiparea principiului sau argument circular. Pe scurt, este adevărat că sunt bogat, pentru că sunt bogat! Explicaţie care, în cazul politicienilor români devine lege. Ex Dictis CTP

P.S. Eu personal nu vreau să mă exprim în această speţă; pur şi simplu consider că nu am destule date încât să am o părere avizată. Aştept alte informaţii, dar în principiu cred că dacă ar fi existat o cale de a demonstra teorema lui Pitagora prin trigonometrie, s-ar fi găsit de mult. Dar pe de altă parte, cine sunt eu să-mi expun aici părerea? Dacă totuşi … Însă, asta nu ar scuti cu nimic superficialitatea patologică a “ştiriştilor” care ne invadează zilnic cu “informaţiile” lor. CTG

Ia uitaţi-vă aici ce minune de formulă matematică au ajuns să vadă unii dintre pământeni (că pe alte planete nu ştiu dacă se difuzează încă):

Imaginea este decupată dintr-una mai mare ce apare pe net în legătură cu un nou serial, Velma, difuzat de HBO, şi care este gândit ca poziţionare temporală înaintea renumitului serial Scooby Doo, dar cu personaje cunoscute din acesta (se numeşte “prequel” chestia respectivă). Pe lângă Velma mai apar ca personaje şi Daphne, Shaggy şi Fred. Căinele lipseşte deocamdată. Din păcate însă, cum se vede, lipseşte şi matematica, deşi personajul principal se consideră a fi unul foarte inteligent. Iată poza mare din care a fost decupată cea de sus:

Tehnic, Velma este un serial animat american de comedie horror pentru adulţi, bazat pe personajul Velma Dinkley din franciza Scooby-Doo, al cărui prim episod a fost difuzat pe 12 ianuarie 2023 (sursa Wikipedia). Un serial horror? Păi, am văzut deja din poza prezentată. Imaginea respectivă ne oferă o idee clară asupra felului în care unii pământenii obişnuiţi, mai ales unii din SUA, îi văd pe cei buni la învăţătură, dar şi felul în care mulţi dau atenţia cuvenită detaliilor ce nu-i interesează (mai degrabă nu o dau). Prin comparaţie, avem aici şi un alt exemplu, din mai vechiul Peppa Pig britanic (primul episod difuzat în mai 2004):

Deci, merge şi corect. Totuşi, să nu generalizăm în impulsul de denigrare a americanilor, pentru că se poate şi altfel. În serialul de mega-succes The Simphsons apar uneori elemente de matematică surprinzătoare, dar asta se întâmplă pentru că în echipa de realizatori există câţiva buni matematicieni. Dacă înţelegeţi engleza, puteţi aprofunda subiectul din filmuleţul de la adresa https://www.youtube.com/watch?v=ReOQ300AcSU, în care aspectele ne sunt explicate de nimeni altul decât Simon Singh (da, autorul renumitelor Marea Teoremă a lui Fermat, Cartea codurilor sau Big Bang, toate traduse la Humanitas). Discuţia evoluează în jurul unui episod în care Homer Simphson se hotăreşte să devină inventator şi pare că “îl provoacă” pe Andrew Wiles (cel care a demonstrat marea teoremă a lui Fermat). q.e.d. Dooby Scoo

P.S. Merită observat că anumite “scrieri” matematice “vedetă” sunt expuse cu diverse ocazii pentru a sugera o anumită stare. Când se prezintă într-o reclamă o profesoară care tuşeşte de atâta predat, atunci pe tabla din spatele ei apare de obicei teorema lui Pitagora (deşi era într-o vreme şi o reclamă cu un profesor care avea o figură geometrică pe tablă, ce părea că avea acolo şi o bisectoare sau o mediană, adică ceva mai “complicat”). La liceu, dacă vrei să sugerezi că un anumit personaj este mai “tocilar”, adică mai inteligent decât ceilalţi, atunci îi asociezi formula de la ecuaţia de gradul II. Ceva gen “ăştia” numai formule complicate le vâjâie prin cap, din acelea cu radicali, cu fracţii şi cu semne neobişnuite (adică delta). Dacă cineva doreşte să evidenţieze un “mic Einstein”, gen Dexter, atunci desigur că îl va asocia cu renumita formulă E = mc² (pe care oamenii normali sigur n-o înţeleg, şi oricum, are şi “la putere”, deci e grea!). Asta vrea să sugereze că este vorba despre un mic geniu.

La începutul anului a apărut pe blogul nostru un comentariu, la un articol mai vechi, din 21.08.2018. Postarea respectivă merge pe două nivele de idei: prima este faptul că suma unghiurilor exterioare se păstrează constant indiferent de numărul laturilor unui poligon (triunghi, patrulater, pentagon etc.), rezultatul fiind întotdeauna 360^o (în suma respectivă se ia desigur măsura unghiului exterior din fiecare vârf o singură dată, de pildă la triunghi A_e + B_e + C_e). Acest rezultat dă şi titlul postării respective. Un al doilea nivel al articolului îl reprezintă o scurtă exemplificare pe această situaţie a felului diferit cum evoluează gândirea elevilor şi a faptului mult mai important că noi la matematică acţionăm la vârstele gimnaziale pe o zonă de graniţă între două tipuri de gândire diferite; astfel, noi ne putem trezi deseori în situaţia că unii elevi sunt încă în gândirea specifică copilăriei, pe când alţii sunt deja trecuţi în forma de gândire adultă. Pentru a înţelege subiectul prezentei postări, merită să citiţi sau să recitiţi articolul respectiv la adresa http://pentagonia.ro/suma-unghiurilor-exterioare/ . Iată aici şi comentariul cu pricina (ce a apărut la sfârşitul postării pe data de 1 ian. 2023):

Părerea mea este că la triunghi avem 6 unghiuri exterioare (2 câte 2 congruente), la patrulater la fel. Când calculăm suma unghiurilor exterioare, nu le luam pe toate?

Ba da, “stimate” coleg, desigur că le luăm pe toate dacă ne dorim să omorîm frumuseţea unui rezultat. Sau, vom accepta rezultatul frumos, dar numai cu preţul încărcării textului, aşa încât rezultatul respectiv să fie accesibil cât mai puţinor elevi. De ce? D-aia! Pentru că putem!

Din cauză de astfel de “scormoneli” de dragu’ scormonitului a ajuns matematica noastră şcolară atât de inumană. De dragul unei rigurozităţi excesive omorîm un rezultat frumos cu care am putea impresiona elevii. Precizez aici – a nu ştiu câta oară – că matematica şcolară este pentru elevi, şi nu pentru profesori. Când ne întâlnim între noi, ca profesori, putem discuta orice, dar aici este vorba despre predarea unor cunoştinţe elevilor; aici vorbim despre arta predării matematicii! (ce lipseşte din păcate multor colegi, anume o atitudine empatică la adresa ELEVILOR, a cât mai multora dintre ei, nu doar vârfurilor). Iar în strădania de a-i impresiona pe elevi şi a le câştiga interesul, noi avem la ora actuală rivali de temut, cum ar fi jocurile pe calculator, facebook-ul sau Tik-Tok-ul. Nu complicând-o, ci prezentând-o cât mai simplu avem şanse să le câştigăm sufletul.

Astfel, 360^o este un rezultat foarte frumos prin faptul că reprezintă exact suma unghiurilor în jurul unui punct, (rămânând însă în spectrul obişnuit de preocupare al elevilor de clasa a 6-a şi început de a 7-a). Desigur că acesta se impune şi prin faptul surprinzător că rămâne constant, în comparaţie cu suma unghiurilor interioare, care creşte cu numărul de laturi. Dimpotrivă, 720^o nu mai este un rezultat frumos din punct de vedere al elevului mediu (elevul mijlociu, cum cu mare drag şi empatie îi numea Hollinger). Orice trece peste 360^o este perceput de către elevul obişnuit ca ceva dificil. Dar, ce să zic, fiecare profesor are dreptul să le prezinte elevilor matematică predată cât de complicat consideră. Părerea mea!

Iniţial, când am văzut comentariul de mai sus am fost foarte supărat. Impulsul a fost să pun imediat în continuarea comentariului o replică. Cele două-trei aliniate de mai sus reprezintă manifestarea în fizic a acestui impuls de replică. Cu cât mă descărcam mai tare, cu atât îmi dădeam seama însă că acest comentariu reprezintă o oportunitate extraordinară de a lămuri nişte aspecte deosebit de importante în predarea matematicii, iar pentru această ocazie deosebită nu pot de fapt decât să-i mulţumesc colegului care l-a făcut. Cine doreşte să afle aceste multe precizări, poate citi în continuare următoarele subiecte.

*

Subiectul 1) Revenind la legătura fenomenologică dintre suma unghiurilor exterioare ale unui triunghi sau patrulater (în general un poligon convex) cu măsurarea rotaţiei în jurul unui punct, aceasta se poate scoate în evidenţă printr-o metodă practică deosebit de interesantă. Desenând la tablă un patrulater convex ABCD trebuie să-i prelungim laturile doar într-un capăt (să zicem chiar în sensul rotaţiei parcurs de notarea vârfurilor). Am evidenţiat astfel câte un unghi exterior în fiecare vârf. Luăm apoi un creion şi îl folosim aidoma unui vector astfel: îl postăm de-a lungul laturii [AB] cu capătul în vârful A şi cu vârful îndreptat înspre B; apoi îl glisăm de-a lungul laturii până când capătul creionului ajunge în B, restul creionului fiind situat pe prelungirea laturii [AB]; apoi îl rotim în jurul vârfului B până când creionul se poziţionează pe latura [BC]. În continuare vom reface paşii văzuţi la latura [AB] la fel şi la următoarele trei laturi, pentru ca în final creionul să ajungă în poziţia iniţială, în urma rotaţiei din unghiul exterior lui A (care – săracu’ – a ajuns ultimul, da nu-i bai!). Analizănd succesiunea de mişcări observăm că creionul nostru a efectuat în fiecare unghi o serie de rotaţii (în acelaşi sens), care cumulate compun o rotaţie completă, deci 360^o.

Metoda exemplificată aici este una pur geometrică bazată pe mişcare, deosebit de clară pentru elevi (dar care nu poate fi redactată într-un mod accesibil în scris). Dimpotrivă, metodele statice, bazate pe scriere şi descriere algebrică a fenomenului sunt însoţite de dificultatea “citirii textului într-o limbă” pentru unii elevi încă străină (vorbesc aici de limbajul codificat matematic), care încă nu face parte din “zona lor de confort”; pentru unii nu va face parte nicicând, aşa încât o metoda ca cea de mai sus reprezintă o uimitoare ocazie de a le accesa unor astfel de elevi gândirea fără a folosii tare mult limbajul matematic abstract.

Această metodă poate fi desigur folosită şi la determinarea sumei unghiurilor interioare. La triunghi creionul va fi în final cu vârful în sens opus, arătând o rotaţie de 180^o, pe când la patrulater creionul va fi în poziţia de plecare. Deoarece însă în mişcarea în jurul patrulaterului a avut loc o rotaţie, se poate vedea că de fapt a avut loc o rotaţie completă, suma (unghiurilor interioare) fiind deci de 360^o.

Părerea mea este că această metodă este potrivită doar la triunghiuri sau patrulatere; de la poligoane cu mai multe laturi ar trebui să ne putem baza totuşi în gândirea copiilor pe metodele mai abstracte (atât din punct de vedere al scrierii, cât şi al gândirii: cea apărută la patrulatere cu împărţirea acestuia în n – 2 triunghiuri, sau una nouă de împărţire în n triunghiuri, atâtea câte laturi, cu vârfurile într-un punct interior poligonului).

Pentru cei pasionaţi de experimente în afara programei oficiale, desigur că şmecheria de mai sus funcţionează şi în cazul unui patrulater concav, doar că în “vârful” concav rotaţia trebuie să fie mai mult de 180^o. Mult mai “excentric”, ar fi să studiem ce se întâmplă cu “suma unghiurilor exterioare” în cazul unui patrulater concav, doar că în “vârful” concav rotaţia este de aşteptat să se desfăşoare în sens invers decât la celelalte vârfuri??? (cred; n-am făcut-o, dar o propun spre “cercetare” colegilor). Asta ne-ar putea ajuta să înţelegem ce ar fi acela unghiul exterior în cazul unui vârf concav!?!?

Subiectul 2) Legat de acel impuls psihologic-social al unor profesori de a-i corecta pe alţi colegi imediat ce-i găsesc o minimă posibilitate de a le interpreta exprimarea greşit, aş dori totuşi să mai evidenţiez câteva aspecte (am mai vorbit de acest obicei urât). Societatea noastră este masiv impregnată de acest obicei. Şefii îşi permit să-ţi facă observaţii cu orice ocazie, doar cu motivul nespus de a te înjosi şi a-ţi arăta “cine este şeful” (am aflat şi de exemple din SUA; se pare că apare peste tot acolo unde o persoană se simte frustrată, mai prejos de ceilalţi şi încearcă să “se ridice mai sus”, înjosindu-i pe ceilalţi). Dacă ceva nu funcţionează bine din vina lor, mulţi şefi tot ţie îţi vor face observaţii; tot tu eşti de vină. Acelaşi fenomen i s-a întâmplat fiului meu (în trefic, la viteză mică, în oraş): un ofiţer de poliţie i-a “sărit” în faţa maşinii, uitându-se în partea cealaltă. Fiul meu a frânat brusc, poliţaiu’ s-a speriat şi tot el s-a răstit la fiu-meu “să fie mai atent” când conduce. Ăsta a rămas “mască”, cu replica nespusă în gând: “păi, dacă nu eram atent, erau deja sub dubiţă!”.

În general, în relaţionarea din orice grup apare extrem de puternic fenomenul de bullying, de agresare – măcar verbală – a celuilalt, ca o componentă esenţială în lupta sălbatică de zi cu zi de poziţionare cât mai sus pe scara socială a grupului. Este ca într-o haită de lupi, unde cel mai agresiv ajunge lupul alfa. Aceste agresiuni gratuite se iau ca exemplu şi se transmit mai departe în societate. Din diferite surse mi-a fost dat să aud de la persoane care s-au reîntors în ţară după mulţi ani petrecuţi prin alte ţări, că în România au resimţit – atât ei, cât mai ales şi copiii lor –mult mai profund această stare de bullying, această constantă stare de agresiune înjositoare la adresa noilor veniţi în grup.

Obiceiul este desigur prezent şi în zona comentariilor de pe internet, oriunde în lume, dar la noi parcă mai avântat ca în alte părţi. La orice articol, după primul, cel mult după al doilea al treilea comentariu, încep să apară atacuri la adresa celor care şi-au expus un punct de vedere asupra articolului de bază. De obicei, aceste atacuri sunt foarte dure, multe dintre ele legându-se de chichiţe de scrire folosite ca dovadă sau aluzie la “incultura” celui care a scris înainte, cu trimiteri la BAC-ul respectivului etc. În “străinezia” a apărut în acest sens denumirea de grammar Nazis.

Subiectul 3) Dar, de unde vine asta? Părerea mea este că – cel puţin la noi – de mulţi ani elevii se simt gratuit şi fără motiv întemeiat agresaţi de către profesori, atât datoriltă subiectivităţii elevilor (“are ceva cu mine!”), cât şi datorită stilului de predare excesiv de autoritar al multor profesori (“că altfel nu învaţă nimic”). Bănuiesc că acest fenomen se întâmplă din vremuri foarte vechi, iar faptul că la noi încă dăinuieşte este o dovadă importantă a “in-evoluţiei” sociale a sistemului nostru educaţional. Este evident că, odată ajunşi adulţi, foştii elevi vor aplica aceleaşi metode asupra celor din jur, inclusiv asupra copiilor (alteori, dimpotrivă, conştientizând superficial aceste aspecte, ei se vor transforma în nişte excesivi protectori, dar acesta este alt subiect). Astfel, acest fenomen a ajuns să se generalizeze la nivelul marii părţi a populaţiei, mai ales datorită faptului că nu a fost luat în seamă de către autorităţi şi organizatori ai “şcolii româneşti”, astfel încât să se pună ca obiectiv naţional anihilarea sa.

Fenomenul acestor agresiuni mai are o faţetă, anume cea a “datului mare”: dacă-i faci cuiva observaţie, scoţîndu-i în evidenţă o “greşeală”, atunci te dovedeşti mai presus decât el. Impulsul de corectare pe baza rigurozităţii excesive a apărut se pare în şcoala românească odată cu reforma din 1980 (când schimbarea exprimării într-o formă mai profund ştiinţifică, mai riguroasă, a devenit un obiectiv oficial) şi, după cum se vede, unii încă nu s-au gândit să se descotorosească de acest urât obicei. Astfel, încă mai are loc acest concurs de “care se dă mai deştept”, ca un fel de bullying între profesori.

Subiectul 4) Revenind la fenomenul cerinţei excesive de exprimare riguroasă, acesta se manifesta încă în urmă cu 10-20 de ani şi îmi permit să dau aici un exemplu tipic în acest sens. Astfel, orice profesor risca să fie corectat şi automat penalizat în faţa tuturor celor prezenţi dacă nu respecta cutumele de rigurozitate a limbajului impuse cu ocazia reformei din 1980. Iată în continuare exemplul “vedetă” la care mă refer.

Pe vremuri exista prin manuale precizarea despre cuvântul rază, cum că acesta trebuie înţeles în funcţie de context, fie ca un segment (în acest caz cercul are “o infinitate de raze”), fie ca lungimea acestor segmente (în acest caz cercul are “o rază”). Din păcate însă principiul nu era respectat şi la alte segmente care au şi un nume special. Astfel a ajuns să fie obligatoriu a folosi cuvântul lungime la diferite segmente speciale, cum ar fi la lungimea înălţimii unui triunghi sau la lungimea catetelor în teorema lui Pitagora (am mai vorbit despre încărcarea gratuită a textului respectivei teoreme cu acest cuvânt inutil). Ca norocu’ că bunul simţ a prevalat, astfel încât nu am fost nevoiţi să ajungem la lungimea lăţimii unui dreptunghi, sau mai rău la lungimea lungimii unui dreptunghi (asta ar fi fost culmea culmilor!).

În comparaţie cu acest exemplu, observaţia de la început a d-lui profesor este de-a dreptul justificată: într-adevăr, în orice vârf există două unghiuri exterioare. Problema este de atitudine: ambele au aceeaşi măsură (sunt egale sau congruente, cum preferaţi), iar în proprietatea cu pricina eu m-am referit la măsura respectivă ca număr, adică la singular. De fapt la singular vorbeşte şi titlul lecţiei oficiale: Unghiul exterior unui triunghi, şi nu Unghiurile exterioare (aici trebuie să vă imaginaţi zâmbetul meu până “după urechi”!). În acest context, mă miră extrem lejeritatea cu care am scăpat de m-ul de la măsura unghiului, sau de alte astfel de elemente de scriere riguroasă (sigur voi reveni cândva în acest sens).

Există şi în alte părţi ale matematicii astfel de momente, când noi trebuie să înţelegem din context exact ce este nevoie, eventual ajutat de o scurtă explicaţie orală (orice dăm în scris elevilor devine automat material suplimentar de copiat, îngreunând textul, fără să mai discutăm de impulsul ulterior de a învăţa totul pe de rost). Iată un exemplu sugestiv în acest sens. În matematica şcolară românească există clar delimitarea între divizorii proprii şi divizorii improprii ai unui număr. Pe de altă parte, în istoria matematicii există acea situaţie fabuloasă a numerelor perfecte, respectiv a numerelor prietene. O prezint foarte pe scurt: se numeşte număr perfect un număr care este egal cu suma divizorilor săi. Se înţelege automat – aproape intuitiv – că această egalitate nu poate avea loc dacă includem în această sumă a divizorilor şi numărul însuşi. Pe de altă parte, divizorul 1 este inclus (deci nu putem folosi terminologia uzuală). Astfel, avem următoarele prime numere perfecte: 6; 28; 496 etc. De pildă 6 = 1 + 2 + 3. Acelaşi fenomen apare şi la numerele prietene, cum ar fi 220 şi 284, fiecare fiind egal cu suma divizorilor celuilalt, desigur fără numărul însuşi (căutaţi şi edificaţi-vă pe internet; aceste numere provin de la Pitagora). Situaţia evocată reprezintă un exemplu magistral în care cineva ar putea desigur să complice lucrurile numai aşa de dragul de “a se da deştept” (cum? păi, de pildă, numărul 28 este un număr perfect pentru că reprezintă exact jumătate din suma divizorilor săi – a tuturor divizorilor). Părerea mea!

Subiect 5) Un alt aspect deosebit de important al întâmplării îl reprezintă ideea rezultatului frumos evocată de curând. O foarte mare parte din elevi trăiesc într-o atmosferă impregnată puternic de emoţii, iar pentru aceştia orice rezultat frumos are efectul de a-i atrage – chiar şi măcar puţin – înspre această lume seacă şi rece a matematicii. Este evident că – dimpotrivă – orice ratare a unei ocazii implicând un rezultat frumos reprezintă o ocazie ratată în a-i atrage pe astfel de copii înspre matematică (şi vorbesc aici de majoritatea elevilor, cum îi mai spuneam uneori, despre corpul central al Clopotului lui Gauss). Oare, există profesori care să considere drept o normalitate în a face selecţia elevilor buni alungându-i pe cei indecişi dinspre matematică, şi oare, tocmai am asistat la o manifestare a unui astfel de caz?

Cum am spus mai sus, 360^o ar reprezenta în acest caz un rezultat frumos. Această afirmaţie are aici mai multe paliere. În primul rând că elevul mediu este deja obişnuit cu 360^o – intră în zona sa de confort, deci nu va reprezenta pentru el un şoc. Singura surpriză este faptul că această sumă a unghiurilor exterioare reprezintă exact o rotaţie completă. Dimpotrivă, 720^o nu este încă în acest moment un rezultat frumos, i-ar speria. De-abia la suma unghiurilor interioare a unui poligon cu mai multe laturi elevii vor ajunge să înţeleagă pe mintea lor sume de unghiuri peste 360^o. Din păcate, aici am ajuns din nou într-o zonă de “teren interzis” la ora actuală, deoarece noua programă nu mai prevede suma unghiurilor unui poligon în general (acesta este însă un alt subiect, dar totuşi, care a fost logica pentru această excludere?).

Astfel, frumuseţea rezultatului se relevă şi la un nivel mai înalt, atunci când elevul ar constata – odată cu creşterea numărului de laturi – că suma unghiurilor exterioare rămâne constantă, necrescând odată cu înmulţirea laturilor, aşa cum se întâmplă la suma unghiurilor interioare.

În plus, aici, la unghiurile interioare, apare şi o altă nuanţă interesantă: de la triunghi la patrulater suma unghiurilor a crescut, astfel încât oricine se aşteaptă ca la creşterea numărului de laturi să crească şi suma acestora. Singura întrebare ce rămâne în acel moment este dacă creşterea a fost de adăugare a 180^o sau de dublare (recomand să zăboviţi puţin la acest aspect ce ţine de dilema cognitivă, reprezentând poate chiar un adevărat conflict cognitiv). Stabilind care este situaţia la pentagon, la hexagon etc. se lămureşte şi respectiva dilemă. Ce păcat că au fost scoase, elevii nemai având ocazia de a parcurge acest proces de gândire.

Subiectul 6) În altă ordine de idei, merită să evoc aici şi un alt aspect, anume atitudinea în care sunt scrise multe din postările mele. Am mai spus-o şi cu alte ocazii: nu am nici cel mai mic venit din acest demers. Lucrez “pro-bono” şi nu mă plâng, fiindcă că o fac cu mare bucurie (pentru fiecare nou articol a trebuit mai întâi să mă edific eu foarte bine, iar acesta reprezintă pentru mine cel mai mare câştig posibil). Dacă cineva simte că eu “mă dau mare” prin aceste articole, atunci cred că se află la adresa greşită. Tot fenomenul pentagonia a pornit în 1997 după un an de stat în Şcoala Waldorf, din bucuria minunilor găsite şi din constatarea uimitoare că cele mai multe din aceste lucruri au fost cândva şi în şcoala românească, dar au fost pierdute pe drum. Fenomenul pentagonia a reprezentat de fapt bucuria şi strădania de a împărtăşi cu colegii profesori de matematică toate aceste elemente noi pentru mine la vremea respectivă. Apoi, cu timpul, pentagonia s-a transformat într-o strădanie de a ajuta la “repararea” predării matematicii, strigătele de ajutor în acest sens înmulţindu-se cu trecerea anilor din toate părţile.

În acest proces eu lucrez foarte mult. O pagină A4 ia lejer 1-2 ore de lucru (sau chiar mai multe), iar la un articol, pentru a fi într-o formă cât mai civilizată, lucrez câteva săptămâni (în cazul de faţă, aproape o lună). Unele serii de articole se apropie de magnitudinea unei lucrări de gradul I (majoritatea materialului fiind generat de către mine, nu preluat din alte părţi). În general lucrez la mai multe articole în acelaşi timp.

Legat de la felul cum scriu eu aceste articole, şi aici merită petrecut câteva rânduri. Există articole în care încerc să tratez cât mai complet subiectul propus. În altele îmi permit însă doar să evoc anumite aspecte, lăsând apoi “în sarcina” onor cititorilor să mai studieze şi să se edifice cu subiectul respectiv. Acest tip de articole are şi avantajul că lasă cititorului bucuria descoperirii şi nu-i dă totul “mură-n gură, pe tavă”. De multe ori apelez la acest stil şi datorită faptului că doresc să atenţionez asupra cât mai multor alte aspecte implicate intrinsec sau întâmplător în subiectul principal. De pildă, aspectele psihologice evocate prin exemplele de la sfârşitul articolului despre suma unghiurilor exterioare, aceste aspecte nu au nimic direct de-a face cu subiectul din titlu; ele s-au nimerit din întâmplare “în acelaşi loc” prin tema din caietele elevilor.

Există aici şi un alt aspect: de obicei mă străduiesc să prevăd diferitele comentarii ce ar putea apărea în mintea unui cititor, iar când reuşesc, atunci încerc să şi dau o replică unui astfel de gând, aşa încât eseul respectiv să fie cât mai complet şi mai edificator. Alteori, desigur, nu am cum să prevăd ce ar putea gîndi un anume cititor, fie că pur şi simplu nu mi-ar trece prin minte aşa ceva, fie că sunt prea puternic preocupat de alte aspecte şi îmi scapă posibilitatea unui anumit gând. Revenind însă la exemplul comentariului ce a cauzat prezenta postare, de când predau această teoremă a sumei unghiurilor exterioare, nici măcar o dată nu m-am întâlnit cu impulsul de a aduna în respectiva sumă ambele unghiuri exterioare din fiecare vârf. Poate “om fi noi mai superficiali”, atât eu ca profesor, cât şi toţi elevii mei. Părerea mea!

Subiectul 7) La toate aceste articole mă străduiesc să fiu cât mai neagresiv posibil (un articol la care lucrez acum în paralel, mi-a ieşit prea agresiv din prima încercare, aşa că planul este să-l reiau, să-l rup în mai multe părţi şi să caut o linie mai obiectivă şi mai liniştită; acelaşi lucru s-a întâmplat şi cu eseul de faţă, la care am păstrat doar aliniatele de început din starea de supărare iniţială).

Din multele întâlniri cu profesori din străinătate, ce ne-au vizitat de-a lungul anilor şcoala, asistând la orele cadrelor didactice, deoarece eram nevoit să particip ca traducător la cei care nu ştiau nici engleză suficient de bine, de la aceşti musafiri din vestul Europei am învăţat că la orice critică vrei să i-o faci cuiva, trebuie automat să-i spui şi o laudă, ceva bun, şi oricum într-o discuţie de analiză nu ai voie să-i spui mai mult de două puncte negative. Paul Olteanu spune chiar că la orice observaţie negativă, psihicul nostru are nevoie de trei observaţii pozitive pentru a se echilibra; aşadar, zice Paul Olteanu, la scorul de 1:1, îi eşti dator celuilalt cu încă două pozitive, cu două laude, pentru a nu se simţi agresat. UAU! Apropos: la mulţi elevi de gimnaziu de la ora actuală se pare că raportul se îndreaptă către 1:5.

Acestea sunt aspecte ce nu se studiază în pedagogia matematică românească (cel puţin nu cât am apucat eu să văd), iar aici avem o cauză evidentă a faptului că mulţi elevi urăsc matematica, anume datorită felului în care profesorii de matematică, fiind de obicei “mai avântaţi” decât ceilalţi datorită presiunii examenelor sau a olimpiadelor, preferă doar să critice şi să scoată în evidenţă nerealizările unui elev (nu discut aici despre aspecte de genul că la matematică trebuie să corectezi greşelile de calcul, pentru că altfel ajungi “pe arătură” cu fenomenul studiat); cel puţin unii dintre profesori procedează prea critic şi nu e de mirare că mulţi elevi ajung să le fie frică sau chiar să urască matematica (dar şi tot mai mulţi elevi sunt mult prea sensibili la ora actuală, îngreunând astfel procesul de conectare matematică).

Sugerez în acest sens lectura mai atentă a pasajului din romanul Măsurarea lumii despre învăţătorul elevului Gauss, la adresa http://pentagonia.ro/suma-lui-gauss-2-povestea-sumei-de-la-1-la-100/ . În urmă cu 200 de ani severitatea dascălilor se măsura în bătăi; acum am mai evoluat, aşa că severitatea unui profesor se măsoară în critici, cel puţin măcar în corectarea elevului în chiciţe de exprimare riguroasă. Iar unii fac aici transferul acestei atitudini şi la adresa altor colegi, cu orice preţ şi de multe ori gratuit. Părerea mea!

De pildă, legat de atitudinea cu care a fost scris comentariul respectiv, doresc să evoc aici şi o întâmplare extremă în acest sens. Începând din 2020 am organizat în fiecare iarnă un curs de trei zile de predare a matematicii în şcolile Waldorf. Iniţial s-a putut lăsă “liber” şi pentru participarea unor colegi din alte şcoli, aşa încât am avut atunci şi doi colegi neimplicaţi în Waldorf. De fapt unul era chiar pensionar. Atmosfera cursului era aşa că eu mă străduiam să le transmit participanţilor cât mai multe din aspectele specifice acestei pedagogii, diferite de cele din pedagogia tradiţională, dar totuşi păstrând o aparentă stare de convivialitate, de “masă rotundă”. Desigur că pentru unii dintre participanţi aceste informaţii erau surprinzătoare, aşa încât mai puneau întrebări. Alţii cu ani de experienţă luau cuvântul şi confirmau cele spuse din cazurile apărute la ei la clase. Colegul pensionar a făcut un pas mai departe, intrând la un moment în polemică deschisă cu mine. Am încercat să aplanez vizibilul “conflict” iar în pauză m-am dus la dânsul şi i-am spus că trebuie să-şi ţină pentru el diferitele păreri legate de anumite puncte în discuţie, că aici ne-am strâns să studiem aspecte legate de Waldorf şi că în acest sens am un parcurs bine stabilit, că nu îmi pot pierde prea mult timp cu altele ce nu au legătură cu linia stabilită conformă cu această pedagogie. Răspunsul său a fost bulversant: eu am crezut că am venit într-un loc liber la “dezbateri”, fiind evident că înţelegea prin dezbateri chiar şi polemici, fiecare “cu părerea lui” şi luptându-se aprig pentru aceasta. Oare comentariul ce a cauzat această postare este reprezintă tot un exemplu din această linie a unor polemici gratuite, de genul “care pe care”? Se prea poate. Din păcate, de obicei însă, aceste polemici nu prea se pot menţine într-o zonă elegantă şi neagresivă. Mai ales atunci când cineva vine cu afirmaţii prezentate ca “evidente” (dimpotrivă, o întrebare lămuritoare ar fi reprezentat în cazul de faţă un comentariu neagresiv, la care aş fi răspuns simplu şi pe scurt). Părerea mea!

Aici este vorba mai degrabă de o anumită mentalitate nocivă, acea de “a căuta nod în papură” cu orice ocazie. Ţin minte un exemplu în acest sens în urmă cu cca. 20 de ani. Eram foarte bucuros de o problemuţă compusă în care datele din text erau “frumoase”: un trapez în care se dădeau înălţimea de 12 şi trei laturi consecutive de 13, 14 (baza de sus) şi 15, cerându-se perimetrul şi aria. Pentru elevul mijlociu aceasta era o situaţie suficient de grea, pentru că o dădeam în perioada de învăţare şi exersare a teoremei lui Pitagora, iar seria respectivă de numere mai îmblânzea oarecum percepţia. Apoi, am primit o observaţie, că există de fapt mai multe posibilităţi de soluţie, deşi elevii vedeau întotdeauna doar forma tradiţională de trapez (cu baza 14 de sus cea mică şi cu baza mare jos, care trebuia calculată; parcă dă 28). Apoi, când am inclus problema în 2006 în culegerea de geometrie, încercând să includ toate variantele, dar şi cu implicarea fără de voie a redactorului de la editură, din problema respectivă a ieşit un dezastru. Pentru că, de obicei, la asta se ajunge când începe careva să scormonească şi să caute “nod în papură”. Constantin Titus Grigorovici

P.S. Încă o dată, mulţumiri colegului pentru acel comentariu, ce mi-a oferit ocazia unei astfel de analize exhaustive a fenomenului (sper că n-am scăpat cine ştie ce aspecte importante).

În urmă cu aproape un an (10 ian. 2022, de ziua matematicii) dl. Profesor Radu Gologan dădea un interviu d-nei Iulia Roşca pe HotNews.ro. Afirmaţiile din acest interviu mi-au atras atenţia puternic, aşa că l-am salvat în întregime în ideea de a-l relua într-o analiză riguroasă. Altele au fost însă aspectele ce ne-au preocupat în vremurile ce-au urmat, aşa încât tot timpul am fost nevoit să fug după alte subiecte decât interviul d-lui Gologan. Totuşi, documentul salvat atunci îmi tot revenea în atenţie, prin valoarea gândurilor exprimate, cât şi prin “densitatea” acestora.

Acum, către lăsarea iernii, “la gura sobei”, cred că interviul respectiv poate fi recitit în linişte (sau citit pentru prima dată), spre luare aminte şi spre aprofundare. Peste 80% din gândurile exprimate (orientativ) ating predarea matematicii. În această postare doresc să prezint şi să analizez părţile respective. Ca să nu reiau apoi diferite aspecte pentru a le comenta, îmi permit să-mi inserez gândurile şi comentariile pe parcursul interviului, ca un fel de o a treia persoană în discuţie.

IR: Cum ați evalua modul în care se predă astăzi matematica și se asimilează cunoștințele în școală?

RG: Se fac eforturi mari pentru umanizarea, să zicem, a învățământului matematic și evident direct transformarea lui într-o disciplină care să placă tuturor și să aducă fiecăruia ceea ce trebuie.

CTG: Într-adevăr, predarea matematicii trebuie umanizată, astfel încât să devină accesibilă şi să aducă satisfacţie tuturor elevilor, nu doar celor de vârf; ora de matematică trebuie să aducă tuturor nivelelor de elevi beneficii pozitive (pe care aceştia să le şi simtă, astfel încât să nu mai urască această disciplină şcolară).

RG: Inclusiv Societatea de Științe Matematice din România în ultimii ani a mers pe ideea de a induce în societate faptul că matematica nu se învață în primul rând pentru aplicațiile sale ci pentru modul în care ea modelează gândirea și face ca omul să poată raționa în situații diferite cu argumente asemănătoare. Asta este de fapt matematica.

CTG: Într-adevăr, în România încă nu este luată în seamă importanţa activităţii din cadrul matematicii ca activitate dezvoltatoare de gândire raţională şi logică. Ca urmare. sunt neglijate complet activităţi matematice deosebite, care sunt dezvoltatoare de gândire, dar nu se dau la examen (sau la diferite concursuri şcolare). Iată câteva exemple din clasele mici gimnaziale: 1) Provocarea neplanificată, deci nepregătită de acasă, de a găsi următorul termen dintr-un şir, ce se dovedeşte apoi a fi Şirul lui Fibonacci, sau a următorului rând dintr-un tabel ciudat de numere aranjate în mod triunghiular, ce se dovedeşte a fi Triunghiul lui Pascal (oricând începând din clasa a 5-a); 2) Preocuparea de realizare cât mai exactă a figurilor geometrice, folosind tot arsenalul de instrumente şi tehnici. Astfel de aspecte nu se dau nici la examene, nici la alte concursuri, aşa că nimeni nu se ocupă de acestea. Dacă exemplele numerice date ar avea doar o influenţă colaterală asupra activităţii matematicii, lipsa construcţiilor geometrice influenţează hotărâtor neînţelegerea gândirii geometrice. Revenind la interviu, citim mai departe:

RG: Exercițiile pe care copiii le fac ca temă să zicem la școală sau în clasă analizând un anumit aspect al matematicii nu înseamnă neapărat că ele se aplică în viața de zi cu zi ca atare, ci ele sunt un exercițiu să zicem ca cel de pian când faci digitație ca să îți înveți mișcările.

Există peste tot dorința de a face matematica aplicabilă. Aplicabilitatea nu înseamnă neapărat în școală, nu înseamnă ca trebuie să facem probleme numai cu terenuri agricole, tractoare și procente, cum era pe vremuri, ci ca exercițiu pentru viitor. Această tendință a existat și când a fost realizat noul format al examenului de evaluare naţională, cu exemple din viața de zi cu zi.

Nu cred că se înțelege bine care este demersul, din păcate. Adică ideea a fost oarecum forțată, venită din diverse părți, a unor oameni care nu sunt experți în matematică. Nu se învață matematica pentru aplicabilitate. Dacă la examenele naționale avem probleme despre cum punem faianță pe un perete asta nu înseamnă că am transformat matematica în ceva uman, ceva pe care copilul o înțelege mai repede.

Matematica suferă – și la noi în special a suferit mulți ani – de o abstractizare exagerată, care vine din folosirea unor notații și noțiuni abstracte. Am insistat foarte tare și foarte multă lume, chiar dascăli, s-au supărat când am insistat ca teoria mulțimilor să nu fie predată din clasele mici pentru că acest domeniu al matematicii nu înseamnă decât o notație și o simplificare a vorbirii abstracte. Nu este nevoie de asta. Copilul mic trebuie să înțeleagă raționamentele. Nu trebuie să fie pedepsit dacă nu știe să noteze anumite mulțimi de numere cu anumite litere.

Deci matematica trebuie să fie umanizată. În țările anglo-saxone, de exemplu, aceste notații nu există, totul este notat (exprimat) în cuvinte. Nu știu dacă rezultatele sunt mai bune, pentru că în țările anglo-saxone rezultatele la matematică nu sunt mai bune ca ale noastre, poate că la nivelul de jos, la nivelul minimal, acolo stăm noi mai prost.

CTG: Da, într-adevăr, în jumătatea din stânga a blocului principal al Clopotului lui Gauss stăm foarte prost; în acea zonă se generează mare parte din situaţiile de analfabetism funcţional şi discalculie, în general ceea ce Peter Gallin din Elveţia denumea “persoane avariate matematic” (vezi perezentare din http://pentagonia.ro/conferinta-peter-gallin/ ), cei care se evidenţiaţi negativ în studiile PISA.

Revenind la excesele scrierilor abstracte, într-adevăr acestea au îndepărtat matematica de posibilităţile elevilor. Iar cu cât elevii stăteau mai mult în faţa ecranelor (televizor, calculator, smartphone), de-a lungul anilor ’90 şi apoi tot mai mult după 2000, cu atât rigurozitatea abstractă a limbajului matematic era tot mai departe de disponibilităţile şi capacităţile elevilor de a le înţelege şi a le cuprinde.

Fără să mai discutăm şi de faptul că şi în ultimii ani procesul de îngreunare a limbajului este continuat pe alocuri (reamintesc aici doar definiţia din ultimii ani a două drepte paralele din clasa a 6-a, care începe cu “două drepte necoplanare …”, deşi ideea de drepte necoplanare ţine ca înţelegere de clasa a 8-a). Să revenim la interviu:

IR: Și cum facem, pentru că la nivel de performanță mereu avem rezultate, dar în rest…

RG: Aici trebuie să înțelegem că este falsă acea idee că nu se poate să nu facem un anumit domeniu al matematicii în nu știu ce clasă. Trebuie să ne adaptăm ca dascăli la ceea ce pot copiii să învețe și să facă. Dacă nu se poate înțelege funcția de gradul al doilea la clasa a noua, atunci nu o facem. Mai degrabă insistăm pe lucruri care îl fac pe copil să înțeleagă lumea mai bine, să raționeze mai bine, să știe să se adapteze mai bine în situații concrete.

CTG: Aici sunt într-u totul de acord şi totuşi nu sunt de acord. Da, ar fi minunat ca profesorii de matematică să poată decide dacă se poate parcurge o anumită lecţie la momentul stabilit de programă sau nu. Din păcate, realitatea este cu totul alta: profesorii trăiesc tot timpul cu “sabia lui Damocles” deasupra capului; oricând un profesor poate fi luat la control dacă şi-a parcurs materia sau nu, la inspecţii de diferite nivele.

Pe de altă parte nici nu putem afirma că toţi profesorii sunt suficient de conştiincioşi încât să poată acţiona în mod responsabil cu o astfel de libertate “în buzunar”. Am întâlnit situaţii ciudate în acest sens, de pildă când am fost contactat pentru un sfat, persoana respectivă dându-şi seama în clasa a 8-a că uitase să parcurgă teorema lui Pitagora în a 7-a. Sau, şi mai rău, aflu de situaţii când lecţiile nu se predau, dar apoi se cer la teste, aşteptarea fiind că s-au parcurs acasă, cu profesorul particular.

Oricum, afirmaţia d-lui Profesor Gologan implică ideea că trebuie parcurse lecţiile măcar până la examen, acestea neputând fi desigur amânate mult prea mult. Exemplul cu funcţia de gradul II poate fi trecut mai degrabă la categoria despre lecţii ce s-ar putea parcurge cu o predare mai umană; la alte lecţii însă principiul se potriveşte mult mai bine (Oh, iar aici prefer să nu deschid lista, pentru că atunci sigur nu mă mai pot opri uşor). Să revenim însă la afirmaţiile d-lui Gologan, unde vedem că de fapt dânsul se referea – se pare – mai mult la situaţia predării în pandemie (interviul avea loc la scurt timp după acea forţat impusă şi controversată vacanţă de toamnă neaşteptată din oct.-noi. 2021).

RG: Această idee care parvine în general de la conducătorii politici, că vai de mine ce se întâmplă dacă pierdem o săptămâna de școală după părerea mea este falsă, și în matematică este falsă. Dacă facem puțin dar bine este mult mai sănătos decât dacă facem tot însă prost, fără să fie înțeles ca lumea. În educația matematică acest proverb “puțin și bine decât mult și prost” se potrivește foarte bine.

IR: Argumentul de multe ori este acela al examenelor – evaluarea națională și bacalaureatul. Trebuie să se bifeze materia.

RG: Acolo este o altă problemă. Din păcate, tot datorită factorului politic, dorința de a demonstra că examenele naționale sunt un panaceu și toată lumea să treacă, să ne lăudăm în fiecare an cu procentele, a transformat examenele în ceva formal. Se uită de acel capitol al matematicii care este educația gândirii. Veți vedea peste tot cărți, teste de același fel de bacalaureat în care nu există mari deosebiri. Și dacă un elev va da peste un alt fel de raționament, nu va ști să îl explice.

Și părinții nu mai vor ca un profesor să explice fundamentul și dedesubturile și frumusețea matematicii ci vor să se facă cât mai bine, să învețe acele trucuri care se dau la examen. Care sunt într-un număr redus. Aici este marea problemă, care a început să devină universală, nu este doar la noi.

CTG: Cu aceste afirmaţii sunt într-u totul de acord. Referirile la legea lui Campbell sunt evidente în aceste afirmaţii (dacă aţi ratat articolul, sau pentru împrospătare, vă recomand postarea http://pentagonia.ro/legea-lui-campbell/ ). În altă ordine de idei, va trebui clar să mai reluăm într-o discuţie separată acest obiectiv puţin băgat în seamă, anume de formare a gândirii obiective raţional-logice în orele de matematică, aspect din păcate tot mai neglijat de către tot mai mulţi colegi, fără să mai discutăm de cum sunt acestea privite de către părinţi sau politicieni, în societate în general, deci de la o vreme chiar şi de către elevii de liceu (“asta la ce ne trebuie?”).

IR: Dar pentru a se ajunge la ce spuneți dumneavoastră, matematica să ajungă la mai mulți copii, este nevoie de o modificare substanțială a materiei, a programei?

RG: Nu cred că este nevoie de o modificare, pentru că de peste 150 de ani în mare programa a rămas ca aceeași și s-a dovedit că este utilă pentru că altfel nu se ajungea la rezultatele excepționale pe care le-a realizat mintea umană – calculator, mijloace de transmitere a informațiilor și așa mai departe. Toate au pornit de la o educație matematică serioasă.

Modul de predare și de abordare trebuie să fie schimbat. Trebuie eliminat de exemplu aceste standarde finite de examinare și de evaluare ale copiilor.

IR: Este nevoie ca disciplinele STEM să fie studiate interdisciplinar? Mai mulți elevi cu rezultate în aceste domenii au vorbit despre asta.

RG: Este corect, iar ei v-au răspuns asta pentru că au dat astfel de teste, testele standardizate americane – SAT, GRE. Ele sunt făcute de agenții naționale private, cu tradiție, și au privire de ansamblu. Probabil că lucrurile acestea trebuie făcute, eu nu sunt adeptul acestei idei de a face școala așa încât matematica să fie automat implicată în fizică, chimie și să nu mai faci separat fizică, chimie. Acest lucru merge foarte bine la clasele primare și poate la până la vârsta de 10-11 ani, apoi modul de gândire la fiecare materie este altul. Poate că pilotat un an, doi, zece, în câteva școli. Trebuie văzută și asta, este o experiență care trebuie făcută.

CTG: Aş mai zăbovi puţin la întrebarea despre ce ar trebui modificată, programa sau predarea? Pentru că această întrebare nu poate fi tranşată atât de simplu. Dl. Radu Gologan accentuează aici asupra accesibilizării predării, pentru că aceasta a ajuns să fie total neglijată, fiind de fapt mult mai importantă decât programa în sine. Exact din acest motiv ţin de fapt acest blog pentagonia.ro – Arta predării matematicii.

Acest subiect merită în sine un articol şi o analiză separată, pentru care însă acum nu este loc (dar mă gândesc foarte serios să mă apuc de lucru cât mai repede de aşa ceva). Îmi permit totuşi o scurtă prezentare a unor metehne ce le observ la ora actuală în predarea matematicii şcolare (fără a emite pretenţia că la acestea s-a referit dl. Gologan). Există în principiu cristalizate două direcţii nepotrivite de evoluţie a predării, care au ajuns să monopolizeze mare parte din orele de matematică:

1) Într-o extremă avem o predare intenţionat teoreticistă cu multe elemente prezentate general deosebit de abstract, mult peste nivelul tuturor elevilor; confruntat astfel de lecţii orice elev are nevoie de explicaţii lămuritoare (de la părinţi sau fraţi mai mari, sau desigur de la profesori particulari). Este evident că acest stil de predare se trage din predarea excesiv de riguros, teoreticistă practicată în anii ’80-’90 în şcolile româneşti. Mă feresc a suspecta o acţiune intenţionată în sensul că elevii să nu înţeleagă nimic, astfel încât să vină la meditaţii, aşa încât rămâne doar o explicaţie de tipul unei preocupări egocentriste a respectivilor colegi înspre o exprimare super-teoreticistă, o exprimare ce sfidează orice empatie, scoţând în evidenţă cel mult o stare patologică la acei profesori.

2) În cealaltă extremă avem o predare rezumativă a principalelor idei dintr-o lecţie, fără nici cea mai vagă explicaţie sau implicare a gândirii. Este vorba de profesori ce consideră că elevii trebuie să primească cât mai pe scurt principalele elemente ale lecţiei, pentru a se putea trece apoi rapid la aplicaţii. Nici urmă de explicaţii care să lămurească elevii de ce sau de unde sunt scoase aceste afirmaţii. În acest sens am ajuns să privim cu mulţumire când unii profesori practică o astfel de predare şi aduc totuşi şi anumite explicaţii lămuritoare. Multe culegeri (“auxiliare”) prezintă astfel de rezumate la fiecare lecţie, în format cât mai scurt (fără nicio explicaţie, la geometrie de obicei chiar fără figurile lămuritoare), iar mulţi colegi profesori preferă să-i pună pe elevi să copieze lecţia din aceste culegeri. Gafa pedagogică este însă că aceste rezumate au fost gândite ca rezumate “a-posteriori” predării lecţiei, nu ca forme de introducere a unor noi cunoştinţe.

Problema mare este că nici una, nici cealaltă din aceste două forme de “predare” nu construiesc gândirea în mintea elevilor, amândouă fiind la fel de păguboase, amândouă necesitând de fapt explicaţii şi muncă ulterioară acasă. Faptul că cele două forme de predare devin tot mai generalizate este şi mai dramatic.

Totuşi – ca să fim cinstiţi, nici modificarea programei nu poate fi complet neglijată. Îmi permit aici să dau un singur exemplu. După ce ne-am luptat atâţia ani ca sistemele de ecuaţii să fie readuse în clasa a 7-a, dar într-o formă mai accesibilă, acum trebuie să sesizăm faptul că apariţia formulelor de calcul prescurtat prima dată doar în clasa a 8-a pune elevii în faţa unei “trepte de gândire” mult prea dificile, prea înalte, oarecum dublă ca înălţime faţă de ce pot cei mai mulţi dintre ei cuprinde, supunându-i pe elevi la o presiune foarte mare în toamna clasei a 8-a. O formă mult mai lesne de cuprins pentru elevul mijlociu ar fi fost ca formulele să apară în primăvara clasei a 7-a, însă doar ca metodă de calcul – aşa se şi numesc: “formule de calcul prescurtat”, urmând ca folosirea lor în mod invers, ca metode de descompunere în factori să apară doar în a 8-a. Revenind la interviul analizat, acesta evoluează în continuare într-o cu totul altă direcţie:

IR: Până la urmă, matematica se poate studia online?

RG: Da, matematica are avantajul că se poate adapta la studiul online, spre deosebire de alte discipline. Sigur că și aici lucrurile sunt un pic mai delicate, în sensul în care s-a văzut, copiii buni și dornici progresează mai bine online, din păcate sub medie lucrurile stau mai prost. Deci nu putem face un învățământ de masă numai online, dar cu vârfurile putem lucra online poate mai bine decât altfel. (…)

CTG: Susţin cu totul acest punct de vedere, pe care doresc doar să-l extind: cu elevul mijlociu şi pe durată lungă învăţământul online nu este defel sustenabil. În plus, afirmaţia d-lui Radu Gologan functionează doar de la anumite vârste în sus. Deja am început să vedem urmările năucitoare ale celor doi ani de predare online (pe scară largă, vreau să zic, pentru că toţi avem desigur şi exemple de cazuri în care online-ul a funcţionat); mult vom mai avea de studiat şi de tras în acest sens. Revenind la interviu, după câteva scurte idei despre ziua matematicii, discuţia revine spre predare:

RG: În 2010, Societatea de Științe Matematice a numit anul acela anul matematicii în Școala Românească și a avut tot felul de manifestări legate mai ales despre ce spuneam la început, schimbarea paradigmei despre matematica în școală – nu se face în primul rând ca să înveți să folosești ci se face pentru o gândire corectă. Am folosit un citat din Moisil atunci: „Tot ce e gândire corectă este matematică”.

IR: Dar ați simțit că acest demers de care vorbiți, acest mesaj este primi cu ostilitate, reticență? Pentru că lumea întreabă „la ce îmi folosește mie să învăț integralele?”…

RG: Exact. Am avut discuțiile acestea chiar cu oameni care au avut o carieră apropiată de matematică, care sunt ingineri informaticieni de vârsta mea, care spun că au învățat integrale și „unde mi-au folosit?” Da, dar fără să îți dai seama, acele exerciții ți-au folosit ca să ai niște judecăți formate în creier pe care le aplici în altă parte. Exercițiul matematic, cu integrale, cu ce o fi cât de complicat, nu este făcut ca să le folosești, mai ales acum când calculator îți poate da rezultatul. Problema este raționamentul pe care îl faci. Nu poți să fii inginer de calculatoare dacă tu nu înțelegi niște noțiuni abstracte de matematică.

Inclusiv pentru copii, joaca asta cu tabla înmulțirii, pe care trebuie să o învețe pe dinafară, este utilă. Plăcerea de a se juca cu numerele este primul semn de talent spre un domeniu în care folosești matematica.

Interviul se încheie cu câteva gânduri despre organizarea olimpiadelor şcolare, şi poate fi citit în întregime la adresa https://www.hotnews.ro/stiri-educatie-25289414-interviu-ziua-matematicii-profesorul-radu-gologan-matematica-nu-invata-pentru-aplicatiile-sale-pentru-modul-care-modeleaza-gandirea-nu-cred-trebuie-modifice-programa-modul-predare.htm Închei cu scuzele de rigoare pentru îndrăzneala de a mă fi inserat cu păreri personale în acest interviu, dar şi pentru mega-întârzierea de aproape un an a acestei prezentări faţă de momentul interviului. Titus Grigorovici

În seria Out of the box, difuzată în emisiunea Lumea Europa fm, dl. Cătălin Striblea îl are la ora actuală ca invitat în fiecare duminică pe dl. Lorand Balint. În prezenta a doua postare inspirată din respectivele emisiuni, mi-am propus să reiau alte câteva gânduri din acel prim episod difuzat duminică, în 11 sept. 2022 (îl puteţi asculta pe podcastul Europa fm la seria prezentată de d-na Iulia Verbancu), gânduri cu care m-am confruntat lucrând la prima parte, la cea despre câte feluri de profesori există.

În prezentarea făcută iniţial, Cătălin Striblea spunea despre Lorand Balint că acesta crede cu tărie în ideea de a inspira oamenii să gândească, deşi dintr-o parte a celor spuse în acel prim episod parca se înţelege altceva. Astfel, despre situaţia de la acel moment din învăţământ (septembrie 2022, în plină dezbatere – una foarte dură – între societate şi Ministrul Educaţiei, pe diverse teme, printre care şi introducerea dreptului Colegiilor Naţionale de a-şi organiza propriile examene separate de admitere), în acel moment Lorand Balint spunea:

LB: Partea bună este că există dezbatere, că în România se încearcă o schimbare sau măcar se discută despre o schimbare, pentru că realitatea în care trăim este că pe întreaga planetă au loc discuţii similare la o scară mai mică sau mai mare. Toată lumea trăieşte într-o nouă realitate. Lumea a devenit mult mai fluidă. Schimbările sunt la ordinea zilei. Un an nu mai seamănă cu anul următor şi nu vorbim despre efectele pandemiei sau a unei crize punctuale, ci este vorba de o realitate deja de zeci de ani de zile, iar sistemele de învăţământ din toată lumea sunt construite pentru o realitate trecută. Şi atunci, ceea ce trăim noi în România, dezbaterile şi conversaţiile sunt la ordinea zilei şi în alte ţări ale lumii. Asta este partea foarte bună, că dezbatem, că discutăm (…) şi este unul din beneficiile apartenenţei la lumea occidentală (faptul că putem să vorbim, faptul că putem să dezbatem, faptul că putem să ne contrazicem, să avem păreri diferite, …).

Într-adevăr, este foarte bine că există dezbatere şi este foarte bine că am ajuns ca societatea să aibă un cuvânt hotărâtor de spus în marile decizii ale guvernanţilor. Am văzut până la urmă cum s-au decis lucrurile, ajungându-se la demisia d-lui Sorin Cîmpeanu.

Legat de ideea existenţei unei noi realităţi cu care se confruntă sistemele de învăţământ, şi cu această idee sunt într-u totul de acord. Aş da aici şi un exemplu, unul deosebit de îndepărtat, atât temporal cât şi preocupaţional, care să ajute la înţelegerea magnitudinii acestor gânduri. Într-un “top” al celor mai tari şi influente jucării sau jocuri ale anilor ’80, difuzat de posturile National Geographic (desigur centrat pe SUA), pe locul 1 este Cubul Rubik. În prezentarea făcută apar două idei deosebit de interesante. În primul rând că firma cu care se discuta pentru producere nu a dorit la început să intre în această afacere pentru că “De ce ai produce o jucărie pe care nu o poţi rezolva???”. Cu alte cuvinte, se considera ca minimă, chiar neglijabilă, forţa copiilor de a rezolva o situaţie ce părea de nerezolvat pentru adulţii aflaţi în posturile de decizie. Realitatea este însă că tinerii, copiii chiar, au alte moduri de a ataca o situaţie nouă, moduri încă neînţelese pe deplin de lumea adultă, moduri cu care ei pot rezolva în mod neaşteptat probleme cu care se confruntă, cu o singură condiţie: să vrea. Deci problema se reduce la a găsi subiecţii care să vrea, pentru că putere au destulă (există în acest sens şi multe alte exemple; aş amini doar că pasul decisiv în descifrarea scrierilor maiaşe a fost făcut de copilul unui cercetător care lucra la acest subiect). Or, sistemul de învăţământ oficial pleacă întotdeauna de la premisa că elevii trebuie învăţaţi de către adulţi cum se face ceva nou. De obicei nu este inclusă în politica educaţională ideea că un copil ar putea găsi singur o soluţie. Aici unii – mai ales pe la noi – s-au obişnuit să scurtcircuiteze brutal sistemul natural al minţii copilului, instituind modelul de a parcurge lecţiile înainte, fie de către un membru al familiei, fie de către profesorul particular, încercând să dea astfel impresia unui copil care gândeşte. Revenind la cuburile Rubik, la ora actuală nu mai se mai poate manifesta această creativitate, pentru că orice copil atras de jucăria respectivă are posibilitatea să caute direct pe youtube, manifestându-şi şi modelându-şi forţa minţii înspre a prelua ceva gata făcut, nu înspre a genera ceva nou.

Este evident că sistemul de excelenţă în matematică practicat în şcolile româneşti este oricum foarte asemănător cu ce am scris anterior: pentru a avea o eficienţă bună în atingerea nivelului ridicat, elevii primesc de-a gata diferite şmecherii, fără ca ei de fapt să le descopere singuri. A lăsa copiii să descopere singuri reprezintă un proces de învăţare foarte lent şi total nesigur; dimpotrivă, a-i arăta o şmecherie, a-i arăta cum se face este mult mai eficient. Copilul ajunge să ştie multe într-un timp relativ scurt, dar el dezvoltă doar abilităţi de stocare şi de manevrare a celor primite. Aceşti elevi sigur nu dezvoltă abilităţi de a genera singuri elemente noi (măcar noi pentru ei, chiar dacă acestea nu sunt noi pentru alţii).

În al doilea rând (evenind la reportajul despre cubul Rubik) odată ajuns pe piaţă, după ce generase acea totală preocupare în lumea copiilor şi a tinerilor, preocupare de-a dreptul obsesivă, copiii “se jucau” tot timpul cu acest cub, găsind rezolvări şi în scurt timp ajungând desigur să concureze între ei, care îl face mai repede. S-a ajuns astfel şi la concursuri şi la consemnarea primelor recorduri. Şi – Atenţie! – totul se întâmpla fără prezenţa internetului; cu alte cuvinte, în primul rând putem fi siguri că soluţiile au apărut de undeva, dintr-o minte, posibil de fapt din mai multe minţi separate de distanţe uriaşe, iar apoi de la aceştia rezolvările se învăţau “prin viu grai”, transmise de la unul la altul (eu de pildă aşa am ajuns să rezolv partea finală, ultimul strat al cubului, preluând nişte scheme de la alţi elevi, prin ’83-’84).

Mie mi-a atras atenţia faptul – nespus în emisiune – că totul se întâmpla “underground”, adică oarecum neoficial, neinclus în procesul oficial de învăţământ. Adică, elevii învăţau matematică brută, grea, gândită iniţal de către profesorul Ernö Rubik pentru studenţi, şi o făceu singuri, fără ghidajul profesorilor. Să ne imaginăm deci profesorii cu materiile lor învechite pe de-o parte, la ore, iar pe de altă parte elevii învăţând ceva nou, intrigant, dar fascinant, venit din exteriorul şcolii, lucrând cu înverşunare în pauze, în ore sub bancă, înainte sau după ore, fiecare singur sau cu prietenii, lucrând la ceva neinclus în sistemul şcolar oficial, dar având clar efecte pozitive asupra propriei dezvoltări intelectuale (vedere şi orientare în spaţiu, educarea voinţei pentru căutarea soluţiei etc.), în ultimă instanţă asupra propriei educaţii. Pentru prima dată elevii se educau singuri, total pe lângă sistemul oficial de educaţie, iar sistemul putea doar să privească uluit la fenomenul respectiv. Desigur că au fost probabil şi minţi deschise printre profesori, care în mod spontan să fi pornit şi ei pe acest drum, atât ca rezolvitori individuali, cât şi ca profesori, încercând unele prime includeri a cubului Rubik în cadrul orelor de matematică, dar îmi permit să cred că aceştia au fost doar câţiva, fenomenul neputând fi ridicat la nivelul de masă, aşa cum avea loc în rândul elevilor (nici chiar într-o ţară ce se pretinde deschisă la nou cum sunt SUA).

Revenind pe plaiuri mioritice, nici până acum sistemul nostru şcolar nu are o strategie de a integra în vre-un fel această jucărie în cadrul preocupărilor oficiale. Oare, o astfel de includere ar trebui să vină de sus sau să fie făcută la nivel local, opţional, individual, punctual în diferite lecţii deja existente? Păi, veţi spune, de vreme ce nu este la examen, de ce să o facem? Dar – voi răspunde – oare noi doar pentru examene lucrăm? Asta este însă o altă dezbatere. Vorbind despre “ce ar fi de făcut” la nivel naţional, adică într-o ţară cu un sistem centralizat de stat, Lorand Balint dădea următorul exemplu:

LB: Mă refer acum … la ceea ce au făcut englezii în ultimii zece ani, când şi-au dat seama că realitatea s-a schimbat, că trebuie să-şi adapteze şi sistemul de educaţie de stat. Ei aveau două scenarii, unul care să le vină de la guvern, de sus, să zică “aşa faceţi!” – şi istoric aşa s-au întâmplat lucrurile – doar că şi-au dat seama că nu prea ştiu exact “cum să facă”; sunt atâtea de multe variabile, atâta de multe realităţi. Atunci decizia lor a fost să meargă pe scenariul 2 în care au dat o mare autonomie şcolilor din sistemul de stat, să se comporte aproape la fel ca şi şcolile din sistemul privat, să poată să ia decizii local, să poată să-şi asume lucruri care diferă de restul şcolilor din sistemul de stat, urmând ca după o perioadă să măsoare, să observe care sunt lucrurile care au funcţionat mai bine şi care au funcţionat mai prost, şi să tragă învăţăturile de la toate, să lase şcolile să inoveze, să caute soluţii şi apoi să le extrapoleze la nivelul sistemului.

Imediat în urma acestui exemplu, fără să ne fi prezentat clasificarea profesorilor (de care noi am discutat deja în prima parte), Lorand Balint trage următoarea concluzie:

În România, dacă este să ne uităm, dacă e să avem inovaţie, dacă este să avem transformări, cel mai probabil colegiile naţionale sunt principalul candidat. Ele sunt cele mai îndreptăţite să caute soluţii şi să inoveze (…).

Ulterior, spre finalul discuţiei, adică după prezentarea celor cinci categorii de profesori, Lorand Balint ajunge să justifice părerea exprimată mai devreme, anume că colegiile naţionale ar fi principalele puncte de unde ar apărea o evoluţie:

LB: …. La colegiile naţionale ponderea profesorilor din categoriile “de şcoală veche” sau “tip-top” sau “dac-aş avea” este mult mai mare decât în restul instituţiilor şi atunci din această perspectivă este mai probabil ca de la ei să vină inovaţia şi să schimbe lucrurile. (…) Creşte probabilitatea ca (în câţiva ani) să apară un model care să poată fi replicat …. .

Un prim răspuns la această afirmaţie ar fi pe o lungime de undă a pamfletelor: Aşa, am înţeles, deci de la Colegiile Naţionale este de aşteptat să apară o soluţie pentru marea masă de elevi analfabeţi funcţionali din mediul rural! Da, bine.

Pe o lungime de undă apropiată, aşputea începe discuţia acestor citate cu o concluzie finală (din punctul meu de vedere): modelul nu ar apărea în câţiva ani, modelul deja există (!), anume la diferite facultăţi (unde, desigur că nu te pui cu autonomia universitară!) Practic, Lorand Balint sugerează aici instituirea discriminantă a unei autonomii preuniversitare, însă doar la nivelul Colegiilor Naţionale.

Să vedem câteva aspecte ale funcţionării autonomiei la nivel universitar, astfel încât să ne putem închipui cum ar funcţiona la nivel preuniversitar. De pildă, dacă doreşti să intri la o anume facultate (la care admiterea are loc pe baza unor examene concrete), atunci cel mai sigur este să iei meditaţii de la profesori din acea facultate, altfel rişti cel puţin ca să intri la “taxă”. Oricum, pentru anumite facultăţi există desigur şi culegerile aferente, pe care trebuie să le cumperi şi după care trebuie să lucrezi, pentru că acestea îţi dau “lungimea de undă” a subiectelor ce le vei primi la examenul de admitere. Iar modalitatea orelor online desigur că nu putea fi ratată în urma extinderii modelului din pandemie. Vă daţi seama ce oportunităţi financiare suplimentare ar apărea pentru cadrele didactice din diferitele colegii, dacă s-ar permite examene separate la acestea? Totul se reduce până la urmă la bani şi la forţa financiară a familiilor care “pun ochii” pe o anumită instituţie pentru nivelul următor de educaţie. Nu că acum n-ar exista fenomenul meditaţiilor în masă, dar o admitere separată la diferitele colegii ar fi ridicat fenomenul la un cu totul alt nivel. Am prezentat pentru început gândurile din acest aliniat, doar aşa ca să înţelegem cum ne situăm faţă de cele susţinute în respectiva emisiune. Pentru că de fapt, despre asta a fost vorba în primul rând în respectiva schimbare faţă de care toată lumea era indignată prin vară, atunci când dl. Cîmpeanu venise cu această propunere, pe care dorea să o impună cu orice preţ.

Permiteţi-mi să trec însă la lucruri mai serioase, anume la analiza punctului de vedere al lui Lorand Balint, anume că plecând de la premisa că la Colegiile Naţionale este desigur o “densitate” mai mare din categoriile dezirabile de profesori, atunci desigur că de acolo ar fi de aşteptat să apară şi idei novatoare bune pentru reformarea învăţământului românesc. Eu sunt doar parţial de acord cu aceasta concluzie.

Totul pleacă de la faptul că linia ghidantă a Colegiilor Naţionale este una orientată mai tot timpul spre excelenţă, spre performanţă în cele două direcţii arhicunoscute: concursurile şcolare, respectiv examenele de final de ciclu şi admiterea la formele şcolare ulterioare. Or, aceste rezultate se obţin exclusiv pe baza elevilor de vârf, cu grijă selectaţi dinainte, dar şi pe baza unei presiuni dure a materiei (cu accent pe cantitatea mare, dar şi pe nivelul ridicat, chiar foarte ridicat), presiune exercitată prin intermediul notelor, presiune ce are de obicei ca urmare faptul că cei mai mulţi elevi au nevoie de meditaţii particulare la materiile pentru care se doreşte performanţa. Or, cum cei mai mulţi profesori de la aceste instituţii lucrează în acest stil, căutând cu înverşunare nivelul foarte inalt (să ne limităm aici doar la matematică, unde cunoaştem bine tabloul), este de aşteptat ca modelele ce ar reieşi dintr-o astfel de căutare novatoare în cadrul Colegiilor Naţionale – sugerată de Lorand Balint – să fie una potrivită doar acestui segment al societăţii, anume elevilor de vârf, respectiv familiilor cu forţă financiară pentru meditaţii.

Cu mare probabilitate putem spune că modelele reformatoare ce ar reieşi din aceste instituţii de învăţământ ar fi potrivite doar şcolilor sau claselor “de elită”, croite după acelaşi model. Nu trebuie să fi “mare filozof” în cunoaşterea învăţământului românesc ca să îţi dai seama că aceste modele nu ar fi aplicabile în clasele sau în şcolile cu elevi “mai de rând”, din oraşe sau din mediul rural, aceştia rămânând din nou “pe de lângă”.

Ce-i de făcut? Păi frâiele unei posibile reforme sunt încă tot “în mâinile” Ministerului. Dar Ministerul, ca instituţie (chiar dacă erau cu totul alţi oameni atunci, pe vremuri), Ministerul ne-a adus în această situaţie în care toate forţele creative ale profesorimii sunt îndreptate doar către elevii cei mai buni ai societăţii, cel mult înspre copiii familiilor celor mai potente financiar. Mă refer aici desigur la continuarea şi la exacerbarea în anii ’90 şi mai departe a politicilor lui Ceauşescu spre excelenţă. După părerea mea, ca urmare tot Ministerul – chiar dacă cel de acum – trebuie să descâlcească această situaţie, are datoria să o facă (deşi se cam codeşte).

Mudificând puţin puctul din care privim subiectul nostru, nu se poate ca acum Ministerul să pretindă că lasă frâiele în mâinile celor mai bine poziţionaţi (cu cei mai mulţi “profesori dezirabili”), de vreme ce aceştia sunt setaţi tot pe vechile obiceiuri şi direcţii. Ministerul este cel care trebuie să reseteze cumva mai întâi tot sistemul pe nişte coordonate mai sănătoase pentru întreaga societate, nu doar pe nişte lungimi de undă favorabile numai elitelor, şi doar apoi, după ce sa dovedit că resetarea a avut loc în mod real, doar apoi Ministerul poate lăsa frâiele din mână.

Iar acest proces de lăsare a frâielor din mână trebuie făcut cinstit, accesibil pentru toată lumea, astfel încât şi dascălii implicaţi în şcolirea celorlalte categorii de elevi să aibă posibilitatea să “renoveze” zona lor de activitate. De pildă, ca să dăm doar un singur exemplu, sunt atâtea persoane (fizice sau juridice) care se implică intens în recuperarea păturilor de elevi oropsiţi de soartă, în prevenirea apariţiei analfabetismului sau a analfabetismului funcţional. De ce aceştia ar fi excluşi (pentru că este evident că profesorii din Colegiile Naţionale nu se întâlnesc cu astfel de situaţii, deci nici nu intră în raza lor de preocupare)?

Conştient fiind că această resetare nu ar putea de fapt avea loc, pentru că societatea este în mare parte calcifiată, osificată în modele vechi, unilaterale, greşite pentru mare parte a elevilor, putem să ne gândim şi la o altă abordare (nu am inventat-o eu, ci am aflat-o de la alţii). De pildă în Norvegia profesorii şi şcolile sunt obligate să treacă la un sistem de predare “prin descoperire”. Adică profesorii nu mai au voie să predea prin “prelegere”, prin prezentare a itemilor.

O formă mai simplistă de căutare a soluţiilor, similară cu cea britanică prezentată de Lorand Balint a avut loc în jurul lui 1980 în Suedia, deci soluţii există, doar să se dorească găsirea lor, doar că interpretarea acestor modele să se facă cinstit, nu deformator, ca în cazul de faţă.

Vreau să spun că Ministerul ar trebui să genereze un cadru de referinţă a învăţământului mai sănătos, în conformitate cu pretenţiile şi cu cerinţele unui învăţământ modern echitabil pentru toţi cetăţenii săi, un model similar cu cele folosite la nivel mondial, şi doar apoi să dea libertatea profesorilor şi şcolilor să caute soluţii în acest cadru. Deşi, şi aici am masive rezerve despre ce modele ar găsi unii sau alţii (văd destule exemple negative în jurul meu).

Atâta vreme cât suntem ancoraţi în obiceiurile şi în formele trecutului, atâta vreme cât inclusiv profesorii de la care s-ar aştepta acţiuni reformatoare pozitive sunt selectaţi tot pe baza criteriilor trecutului, sigur nu se vor putea găsi forme noi de şcoală şi de şcolire care să fie eliberate de tarele trecutului. Revenind la emisiunea analizată, spre final mai are loc o bucăţică de “discuţie discutabilă”:

CS: E important să ai o elită consolidată sau o masă mare de elevi absolvenţi în România care ştiu să lucreze la nivel mediu?

LB: Mie-mi place “şi-ul” (şi o să mai apară în discuţiile noastre); eu mă feresc de “sau”. Eu cred că poţi să ai şi o elită şi o masă mare de elevi care să fie oameni foarte bine educaţi, cu un viitor foarte bun. Dar este loc de “şi”, adică şi de o elită şi România are nevoie de o elită, de oameni educaţi, de oameni care să împingă lucrurile, de oameni care să fie pasionaţi, să aibă un mediu în care să se dezvolte.

Deci, d-lui Lorand Balint îi place “şi-ul”, dar iată ce ne transmite dânsul de fapt în ultima frază a emisiunii: ne spune că trebuie să ne preocupăm atât de elită (şi GATA!).

Simţiţi că ceva este greşit la fraza de mai sus? Poate corect ar fi fost să scriu: trebuie să ne preocupăm atât de elită, cât şi de ceilalţi (alegeţi dvs. eventual o altă formă de frază care să vi se potrivească, dar să aibă şi sens). Dar, din păcate, în argumentaţia din fraza finală a lui Lorand Balint lipseşte cu desăvârşire referirea la marea masă a absolvenţilor care să ştie să lucreze onorabil la un nivel mediu (apare doar în penultima frază). Poate că dânsul a vrut să o zică, poate că a subânţeles-o, poate s-a luat cu vorba, vrând să spună cât mai multe (vorbeşte foarte repede şi foarte mult), dar de spus n-a spus-o în final; nici măcar un cuvinţel! Chiar dacă susţine că este un adept al lui “şi” în loc de “sau”, se pare că Lorand Balint cam înclină spre zona elitelor (la fel ca mai toate persoanele ajunse în poziţii decizionale în ultimii 30-40 de ani în România).

Îmi pare rău, dar în urma acestei ultime pledoarii din finalul emisiunii respective, din partea mea dl. Lorand Balint primeşte doar un foarte apăsat semn cu pumnul strâns şi cu degetul mare în jos! Pentru mine persoanele care nu se gândesc şi la marea masă a elevilor, la corpul principal din “Clopotul lui Gauss”, pentru mine aceştia sigur nu contează în a emite păreri despre cum ar trebui să arate viitorul şcolii româneşti. Este absolut natural să ne procupăm de elite (să dăm Cezarului ce-i a Cezarului), o merită din plin, dar suntem obligaţi să ne preocupăm cel puţin la fel de mult şi de ceilalţi. Iar, ţinând cont că principalul curent de preocupare a fost în ultimii 30-40 de ani doar înspre elite, înseamnă că ar fi vremea să lăsăm ceva timp şi preocupării pentru restul populaţiei şcolare.

De fiecare dată când se naşte o discuţie despre ce ar trebui să facem cu restul populaţiei şcolare (de pildă pe baza procentelor răvăşitoare de analfabetism funcţional dovedite de Studiul PISA), repede sare cineva în sus “dar elitele noastre?”. Cu elitele trebuie să se lucreze mai departe conform nevoilor lor (iar despre acestea nu-mi fac griji, sigur preocuparea va continua pe lina deja cunoscută, şi este ok aşa), dar marea discuţie este despre ceilalţi, despre cei ce nu pot face parte din rândul elitelor. Despre aceştia discuţia trebuie lăsată să aibă loc, trebuie lăsată să se dezvolte, ca apoi să ajungă să se genereze soluţii, iar pentru asta trebuie încurajată şi mai ales statutată la nivel naţional oficial.

Ca o părere personală, din păcate se pare că procesul de “a lăsa frâiele din mâini” din partea Ministerului a cam pornit, fără să fie clar anunţat şi nici bine organizat. Iar mişcarea respectivă cu intenţia de a da Colegiilor Naţionale dreptul să-şi organizeze propriile examene de admitere făcea parte din acest proces, ca un fel de start furat (cum ar fi la Formula 1 înaintea unui restart, dacă nu s-ar anunţa decât unii şoferi că Safetycar-ul se va retrage). CTG

P.S. După cum am scris, în prezentarea făcută iniţial, Cătălin Striblea spunea despre Lorand Balint că acesta crede cu tărie în ideea de a inspira oamenii să gândească. Da, pe mine dânsul m-a făcut să gândesc, dar sigur nu în direcţia în care şi-a dorit-o. Dar, lăsaţi-mă pe mine la o parte. Să încercăm să ne imaginăm cum ar ajunge să gândească marea masă a elevilor acestei ţări într-un viitor organizat după modelul previzionat conform acestui interviu? Păi, simplu: la fel cum gândesc şi marea masă a actualilor adulţi (foştii elevi de ieri), deoarece condiţiile de formare ar fi identice. Exact la fel, atât cu bune, cât şi cu rele, dar sigur cu nimic în plus, cu nimic mai presus.

P.P.S. Mai recent, într-o emisiune din 13 noiembrie, Lorand Balint se arăta mult mai raţional. Astfel, în emisiunea în care discutau fenomenul doritorilor de carnet de conducere auto, care sunt însă analfabeţi, dânsul spunea ceva de genul: trebuie să înţelegem realitatea în care trăim şi să ne-o asumăm, sugerând găsirea unor soluţii Out of the box. Într-adevăr, cu aşa ceva sunt într-u totul de acord. Dar, oare când va începe şi în organizarea învăţământului românesc, în particular a învăţământului matematic, un proces de găsire a unor soluţii Out of the box? Haideţi să luăm această recomandare şi să o aplicăm şi asupra situaţiei matematicii şcolare din România. Cât mai mulţi dintre noi! (cu scuzele de rigoare pentru critica efervescentă, dar şi cu mulţumirile corespunzătoare pentru gândurile exprimate de dl. Lorand Balint în emisiunile respective)

În seria Out of the box, difuzată în emisiunea Lumea Europa fm, dl. Cătălin Striblea îl are invitat pe dl. Lorand Balint. Acesta este un om care crede cu putere în puterea educaţiei, ca să-l citez pe Cătălin Striblea din prezentarea făcută la început. Seria Out of the box a pornit cu câteva discuţii despre educaţie, după care s-a distanţat de acest subiect (în episodul al doilea au vorbit despre motivele din cauza cărora elevii îşi scot scutire la Educaţie fizică).

În prezenta primă postare redactată cu mare întârziere faţă de difuzarea respectivei emisiuni, mi-am propus să reiau câteva gânduri din primul episod, gânduri la care tot cuget de atunci (episodul a fost difuzat duminică, în 11 sept. 2022; îl puteţi asculta pe podcastul Europa fm la seria prezentată de d-na Iulia Verbancu).

CS: Ştiu că tu ai un tip de studiu făcut prin munca ta, despre profesorii din România, că sunt mai multe categorii de profesori. Poţi să ne spui despre asta?

LB: În momentul în care am avut de făcut o serie de proiecte despre profesorii din România am petrecut foarte mult timp să-i înţelegem, pentru că nu există acest lucru “Profesorul român”. Avem profesori diferiţi şi tipologii diferite şi sunt implicări diferite. Am identificat cinci tipologii diferite de profesori.

1) Prima categorie sunt profesorii blazaţi, sunt cei care au ieşit deja la pensie, chiar dacă au 25 de ani, 30 de ani sau 60 de ani, vârsta este mai puţin importantă; pentru ei totul e greşit, orice s-ar face bifează şi se duc, eventual intră la oră; trece ora, au rezolvat-o, vine salariul, îşi văd mai departe ….. . Ăsta este un segment care de multe ori blochează iniţiativele, pentru că “nimic nu-i bun, nimic nu se poate face, totul e greşit, sistemul e greşit, oamenii sunt greşiţi, copiii sunt greşiţi”; totul e greşit pentru ei.

2) Al doilea segment sunt profesorii de şcoală veche. Sunt oameni foarte faini, foarte implicaţi în educaţie, care cred în educaţie, dar care sunt ancoraţi într-o lume un pic depăşită, adică au metodele care le aveau în trecut. Principala lor plângere este că elevul din ziua de azi nu mai este “cum era odată” şi atunci au dificultăţi în a se înţelege cu ei, deşi sunt implicaţi, deşi sunt profesori din pasiune.

3) Al treilea segment – profesorii “tip-top” le-am zis noi, sunt cei care sunt şi implicaţi şi fac lucrurile, caută pe internet, interacţionează cu copiii, încearcă să-i înţeleagă, încearcă să-şi dea seama care sunt metodele noi de predare şi de interacţiune.

4) Al patrulea segment ar fi segmentul profesorilor “băi, dac-aş avea!”: “dac-aş avea şi eu 15 copii la sala de clasa în loc de 30, dacă aş avea şi io un proiector şi-un lap-top şi internet care să funcţioneze permanent, dac-aş avea nişte resurse, aş faaace. Practic sunt oameni care poate, la un moment dat au fost “tip-top”, au avut energia, dar după aia a venit o inspecţie, a venit poate reacţii de la nişte părinţi care n-au fost încântaţi că au încercat lucruri un pic diferite, şi au început să fie mai “dac-aş avea, dac-ar fi, dacă …”.

5) Ultimul segment (şi cel mai mare segment) sunt profesorii: “dacă mi se spune, asta voi face”. Acesta este cea mai mare parte, da! Sunt cadrele didactica care sunt cadre didactice pentru că acolo i-a adus viaţa. Adică nu sunt neapărat implicate, neapărat să-şi dorească să fie profesori, dar sunt acolo. Iar ei respectă: dacă programa zice, dacă vine inspectorul şi zice “asta trebuie să faceţi”, ei o să facă ceea ce li se spune, disciplinat; inspecţia a ieşit bine, şamd .

Deci să le recapitulăm: (1) profesorul blazat, (2) profesorul de şcoală veche, (3) profesorul “tip-top”, (4) profesorul “dac-aş avea” şi (5) profesorul “băi, dacă mi se spune fac”.

Mie mi-a plăcut foarte mult această idee, a clasificării atitudinii şi comportamentului profesional al breslei noastre. M-am gândit foarte mult de la acea emisiune la faptul că – uite – şi altcineva a observat că ne comportăm diferit în viaţa de zi cu zi în şcoală. Chiar şi categoriile depistate îmi plac ca idee. Pe unele le-am observat şi eu, pe altele poate creierul meu a refuzat “să le vadă”; dacă Lorand Balint şi colegii săi au lucrat cu grupuri mai mari de dascăli, atunci însă nu le-au mai putut ocoli cu privirea.

Pe de altă parte, într-o şcoală alternativă deosebit de complexă cum este sistemul Waldorf, eu am avut ocazia să mai observ şi alte “patern-uri” (modele) comportamentale, care ţin de felul cum se oamenii comportă puşi brusc şi nepregătiţi suficient într-o comunitate construită liber şi neierarhic. Unele se regăsesc şi la Lorand Balint, altele apar în plus în aceste condiţii noi.

Da, iar acum vine marea întrebare: dvs., stimaţi cititori, din care categorie faceţi parte? Se poate să alegeţi o categorie clară, sau se prea poate să fiţi un mix între două categorii de mai sus, poate o categorie dominantă şi una secundară. Dacă ar fi să mă încadrez forţat în categoriile mai sus prezentate, eu personal m-aş vedea ca un mix între categoriile 2 şi 3, undeva între profesorul de şcoală veche şi profesorul tip-top; cel puţin în parte, pentru că mă văd totuşi şi având diferenţe majore faţă de descrierile tipologice făcute în respectiva emisiune (poate ar mai trebui să studiez pe tema acestora).

Revenind la categoriile de mai sus, nu mă pot abţine să nu observ relativa dezordine în care acestea ne-au fost prezentate, atât felul în care ne-a fost prezentată fiecare individual (eu m-am străduit să redau discursul cât mai fidel), cât şi ordinea acestora. Legat de ordine, singurul lucru la care mă duce mintea ar fi că acestea ne-ar fi fost prezentate în ordine crescătoare (dată fiind precizarea că ultima categorie este cea mai consistentă numeric).

Tot în această emisiune Lorand Balint aduce în discuţie ideea că o parte dintre profesori ar putea fi folosită ca bază reformatoare a învăţământului, adică într-o reformă “de jos în sus”, în pofida existenţei celorlalţi care acţionează oarecum ca o piatră de moară legată de “gâtul învăţământului românesc” (comparaţia îmi aparţine). Astfel dânsul evidenţiază ca aducătoare de speranţă reformatoare profesorii din categoriile “de şcoală veche” sau “tip-top” sau “dac-aş avea”. O astfel de ordonare, pornind de la cei mai demni de încredere la cei mai indezirabili ar fi mai interesantă pentru un studiu despre ce-i de făcut cu şcoala românească. Desigur că aici ar fi importantă şi proporţia în care a fost regăsită fiecare categorie în studiile efectuate.

Adăugând acestei structuri o a treia axă, anume o axă a dezirabilităţii – care categorie ar fi mai de dorit – putem simţi în ordonarea lui Lorand Balint o structură asemănătoare cu Clopotul lui Gauss, cu probabil cea mai deschisă spre acţiuni novatoare în centru şi cele mai retrograde la extreme (retrograde din punct de vedere a implicării în starea calitativă a învăţământui).

Revenind la “poziţionarea” mea în sistemul acestor cinci categorii, eu văd şi o altă nuanţă, anume că categoria “tip-top” sunt de multe ori persoane ce se aruncă cu mare avânt în metode noi, fără ca neapărat să şi aibă certitudinea solidităţii acestor acţiuni, lăudându-se însă masiv cât sunt ei de novatori. De astfel de tendinţe eu mă distanţez. Ţin minte exemplele ce le primeam în mass-media prin aprilie-mai 2020 despre profesorii care aveau deja pusă la punct o formă de predare online cu elevii la diferite licee din ţară (chiar dinaintea pandemiei), profesori care ne erau prezentaţi drept exemple de bună practică. Realitatea ulterioară a arătat însă că acest model de predare, extins la scară generală şi pe durată, s-a dovedit extrem de dăunător la anumite vârste şi peste un anumit prag de folosire. Am dat acest exemplu ca să înţelegem că “nu tot ce zboară se şi mănâncă”.

Am şi un exemplu opus. Doar pentru că pedagogia Waldorf este relativ nouă în sistemul românesc de învăţământ, mulţi aveau tendinţa să spună despre mine şi colegii mei că “folosim metode noi”. Poate erau “noi” pentru ei, inclusiv pentru ei inspectorii, doar că eu regăseam multe metode preluate din sistemul Waldorf din vest şi în manualele sau în culegerile româneşti din anii ’60-’70. A fost o vreme când mă străduiam să le explic că eu nu folosesc metode “noi” ci că folosesc metode “săntoase”, dar după câţiva ani m-am săturat şi m-am retras din astfel de discuţii (din păcate însă, în România încă nu a avut loc o dezbatere reală despre ce ar însemna – de pildă la matematică – o predare sănătoasă).

Închei cu un exemplu despre prima categorie, respectiv despre ultima, adică despre cele două oarecum cele mai retrograde din punct de vedere al ideii de auto-reformare a activităţii noastre (aşadar, două categorii într-un exemplu). Despre auto-reformare vom vorbi mai multe în a doua parte a acestei discuţii.

Fiind oarecum rupt de detaliile din programa gimnazială (dinainte de 2017), în urmă cu câţiva ani am întrebat un coleg de la o altă şcoală dacă se face în clasa a 6-a reducerea termenilor opuşi într-o sumă de numere. Răspunsul a fost că nu se fac, pentru că nu sunt în manuale, în programă etc., că se fac doar în clasa a 7-a. Pe mine m-a mirat mult, pentru că acest pas matematic mi se pare unul de bun simţ, accesibil gândirii copilului din acel moment, uşor de înţeles şi aducător de multă bucurie în viaţa matematică a elevilor (este aşa o bucurie mare în clasă atunci când elevii văd cum o astfel de sumă de multe numere pozitive şi negative se “auto-anulează” măcar parţial, scurtându-se fără nici cel mai mic efort calculaţionar). Făcându-se doar în clasa a 7-a la calcule cu litere sau cu numere iraţionale există clar pericolul ca elevii să priceapă că doar acolo se pot face reduceri de termeni opuşi. Ţin minte cum m-a şocat starea de completă platitudine ce se simţea din acel răspuns. Înţeleg acum că ce am simţit atunci a fost un mix (năucitor pentru mine) între profesorul “blazat” şi profesorul “dacă mi se spune fac”. Apropos de starea de “deja pensionat” mental, despre care vorbea Lorand Balint la început, menţionez că acest coleg acum chiar se pensionează de-adevăratelea. CTG

P.S. Am redactat acest articol cu trei săptămâni în urmă şi de atunci observ aproape involuntar atât diferiţi colegi, care în ce categorie s-ar integra prin atitudinea sa, cât şi pe mine cum manifest în diferite situaţii una sau alta dintre apucăturile celor câteva categorii ale lui Lorand Balint. Nu ştiu dacă aceasta ar fi cea mai bună clasificare, dar ideea acestei clasificări se poate dovedi deosebit de bună în studierea fenomenului învăţământului, mai ales în vederea luării deciziilor realist cele mai potrivite pentru viitor (desigur cu conexiune înspre toate categoriile implicate în procesul şcolar, atât cele implicate direct, despre care am vorbit deja în vacanţă, cât şi despre cele de care încă n-am apucat, dar de-abia aştept să o fac, cu toate calităţile fiecăreia, dar mai ales şi cu toate tarele, deficienţele şi lipsurile fiecăreia).

Îmi vine greu să mă laud, dar chiar sunt surprins. Iniţial am gândit demersul de a susţine un blog despre arta predării matematicii pentru 2-3 ani (pentru atâta aveam idei la început). Exista în subconştient şi visul de a reuşi să public 5 ani (suna frumos: pentagonia – 5 ani). Atâta rezistasem la precedenta încercare, cea cu Caietele de matematică P3NT4GON1A (1998 – 2002). Fiecare an trecut peste acest prag de cinci reprezintă pentru mine o mare realizare în sine. În ultimii doi ani, pe care putem să-i privim ca un bonus, a scăzut frecvenţa postărilor, dar în schimb a crescut considerabil lungimea textelor publicate.

La acest moment aniversar aş dori să evoc un aspect interesant din munca la articolele scrise. Se întâmplă uneori să mă apuc de lucru, încercând să explic un fenomen pe care-l simt eu sau pe care-l găsesc evocat în diferite surse, dar neclar lămurit. Încep să scriu articolul, străduindu-mă să explic ce-ar trebui înţeles acolo, şi din senin îmi apare o idee lămuritoare, sub forma unei expresii ce clarifică foarte bine totul. Restul este apoi doar muncă de detaliu şi de folosire la maxim a noii expresii proaspăt generate (pentru a se fixa cât mai bine în conştienţa cititorului, dar şi pentru a extrage maximum din aceasta).

Ca exemplu cel mai recent, vara asta am avut din nou un moment de inspiraţie în acest sens, generând noţiunea de “Dilemă cognitivă“, ce mi s-a părut mult mai potrivită în folosirea de zi cu zi la clasă, decât poate prea durul “Conflict cognitiv”. Acesta este doar ultimul dintr-un şir ciudat de momente inspiraţionale apărute “din senin” în procesul de explicare a diferitelor aspecte pe care iniţial doar le intuiesc, doar “le simt” mai mult sau mai puţin conştient (dar pe care cu mare avânt mă apuc să le explic colegilor, pentru că simt că trebuie să o fac).

Prima dată s-a întâmplat acest fenomen pe la începuturi, în momentul când am realizat că “Gândirea aritmetică” este profund diferită faţă de “gândirea algebrică“. Apoi am avut un moment interesant când am generat noţiunea de “Matematică naivă“. Altă dată, prin toamna lui 2017, răsfoiam o carte veche a lui Eugen Rusu şi eram entuziasmat de nuanţele nou înţelese la această lectură, când brusc s-a cristalizat ideea că eu folosesc de fapt “Criteriul psihologic al intuiţiei” în selectarea teoremelor pe care le selectam spre demonstrare la clasă. Cu altă ocazie, încercând să explic ce lecţii de geometrie se potrivesc căror elevi, am început să scriu din senin despre “Geometria aritmetică” (geometria de calcul, accesibilă elevilor slabi în opoziţie cu “geometria demonstrativă“, căreia îi fac faţă cu succes doar elevii mai buni). “Predarea prin descoperire” este o altă denumire generată personal, deşi sunt convins că ar trebui să fie de găsit pe undeva în marea şi larga bibliografie pedagogică.

Deşi nu-mi aparţine, sunt foarte bucuros de atenţionarea la adresa comunităţii matematice şcolare româneşti a fenomenului denumit generic drept “Legea lui Campbell” (oare când vom vedea şi efecte în acest sens, în politica educaţională naţională?). La fel de tare m-am bucurat şi de orice alte elemente adusă în faţa dvs. din diferite colţuri ale lumii sau din diferite epoci, elemente ce ar putea contribui la îmbunătăţirea artei predării matematicii.

Dar, pe departe cea mai mare bucurie în uurma acestor articole o reprezintă propria evoluţie ce are loc cu aproape fiecare articol metodico-didactic nou scris. Străduindu-mă la fiecare astfel de eseu să explic fenomenul respectiv cât mai bine, cât mai clar, din toate punctele de vedere, în final mă asigură că eu le-am înţeles foarte bine. Este ca şi cum aş da de fiecare dată un examen în faţa dvs., a cititorilor în mare parte necunoscuţi, mulţi deosebit de pretenţioşi, poate unii în disacord cu mine, aşa încât trebuie din start să fiu cât mai convingător, să aduc argumente cât mai solide, pentru a fi sigur că – odată publicat – trec “examenul”.

În acest sens – din tot acest proces de desluşire a fineţurilor artei predării matematicii – este evident că cel mai câştigat sunt eu, iar acesta este probabil unul din motoarele principale ale continuării blogului pentagonia.ro. Eu muncesc masiv la aceste articole, dar tot eu sunt şi foarte câştigat în final, în sens profesional. Satisfacţia trăită în urma finalizării unui astfel de articol este deosebită, iar asta îmi dă o energie ce mă încarcă puternic în viaţa profesională (fără să mai discut despre calitatea muncii mele, care tot creşte).

Totuşi, sper că măcar frânturi din tot ce scriu eu aici să vă ajute şi pe dvs., cel puţin din când în când. Oricum, stimaţi cititori, ţin să vă mulţumesc din suflet pentru timpul acordat prin lecturarea acestor esuri. Dvs. reprezentaţi desigur celălalt motiv principal al demersului acestui blog. Cu tot respectul, din Pentagonia, al dvs. Constantin Titus Grigorovici