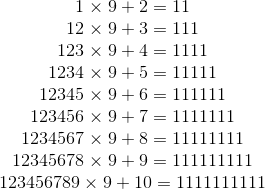Category: Probleme și exerciții

În continuarea explicaţiilor din postarea precedentă pe tema repetării calendarului, doresc să vă prezint în această ultimă parte notiţele mele din zilele de început a anului 2017, atunci când am rezolvat această problemă. “Marea idee” a fost să figurez cei şapte ani normali pe un cerc, la fel şi cei şapte ani bisecţi posibili. Iniţial am încercat parcursul unei perioade de 28 de an pendulând pe cele două cercuri după principiul: trei paşi succesivi pe cercul calendarelor normale şi un pas (dublu) pe cercul calendarelor bisecte. Astfel am obţinut prima dată lista succesiunii celor 14 calendare posibile într-un ciclu de 28 de ani după care succesiunea începea din nou de la capăt:

a, b, c, F, f, g, a, E, d, e, f, D, b, c, d, C, g, a, b, B, e, f, g, A, c, d, e, G, → a

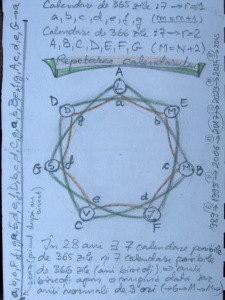
Cel mai interesant în acest şir este faptul că un calendar – de exemplu cel notat cu a – nu se repetă echidistant (nici nu avea cum, 28 nefiind divizibil cu 3), ci într-un ciclu de → 6 ani→11 ani → 11 ani →. Anii bisecţi apar doar o dată într-un ciclu de 28 de ani. Singura provocare în acest moment a fost dorinţa de a cuprinde într-o singură formă circulară (de fapt heptagonală) cele două cercuri de calendare. În imaginea alăturată vedeţi rezultatul acestor strădanii, împreună cu notiţele colaterale din acel moment. De pildă, vedeţi în partea dreaptă o primă încercare de a stabili care au fost precedenţii trei ani şi următorii trei ani care au calendarul identic cu anul 2017. Astfel, au acelaşi calendar anii 1989→1995→2006→2017→2023→2034→2045.

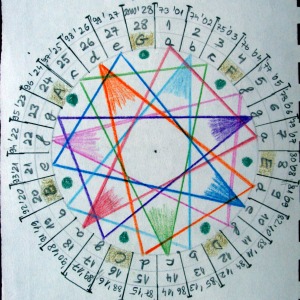
În acest moment este evidentă nevoia de a cuprinde într-o imagine circulară repetitivă, în care să se vadă imediat care sunt anii cu calendare identice, respectiv să vedem fizic ce formă are ciudata periodicitate (6, 11, 11). Astfel, pe figura următoare se vede aranjarea pe un cerc împărţit în 28 de părţi (centura mijlocie) a celor 14 calendare posibile (şapte normale, fiecare de trei ori, respectiv cele şapte bisecte, fiecare o singură dată) pe centura interioară. Pe centura exterioară sunt notaţi în mod corespunzător anii actuali, dar şi precedenţii cu 28 de ani în urmă (pe poziţia 1 anul ’01 pentru 2001 etc., cât şi 2001 – 28 = 1973, notat ’73).

Surpriza a apărut când am început să conectez cu o aceeaşi culoare poziţiile celor trei ani identici dintr-un ciclu de 28, obţinând acele triunghiuri isoscele, a căror combinare arată foarte “mistic”. Efectiv arată ca şi cum m-aş fi întors de la un curs de specializare din Tibet. Pe baza acestei imagini putem stabili imediat că actualul calendar (2017) va putea fi folosit din nou în 2023, pe când calendarul anului viitor de-abia în 2029.

Ultimul pas în această mică cercetare a fost să caut ce se găseşte pe internet legat de repetarea calendarului. Fără pretenţia unei căutări exhaustive, totuşi nu am găsit teoria mai sus prezentată, ci doar câteva tabele cu confirmarea rezultatelor (pentru întreaga perioadă de aproape două secole până în 2100, an ce nu va fi considerat bisect). Cuvinte de căutare ar fi same calendar (pentru engleză), respectiv identische Jahre (pentru germană).

În caz că nu aţi ajuns şi dvs. la aceste concluzii, vă doresc să petreceţi clipe plăcute în procesul de de descifrare a notiţelor prezentate. Ah, da, şi fiţi vigilenţi la calendare vechi. În plus, este evident că un calendar frumos merită ţinut, pentru că îi vine vremea din nou.

Titus Grigorovici

Ştim, copiii urăsc tabla înmulţirii, urăsc cărţile, lecturile suplimentare, memorarea şi dacă s-ar putea nici un fel de manuale, nici un fel de teme, nici un fel de BAC, cu toţii direct la facultate, fără examen de admitere, bineînţeles. Dar, lăsând la o parte cum vor unii din minister să bramburească învăţământul şi sistemul de educaţie, acesta “sfânt”, care “dă profilul unei naţii”, să recunoaştem că aritmetica, tabla înmulţirii, chiar dacă n-o fi ea frumoasă, este totuşi necesară.

Numai că uneori ai nevoie de profesori dedicaţi care să ştie să-i facă pe elevi să descopere frumuseţile matematicii. Ştim, aceştia sunt ca diamantele, nu se găsesc la orice colţ de stradă, dar când ei există parcă mai avem un licăr de speranţă. Iată un exemplu prin care învăţătorii sau profesorii devotaţi meseriei lor l-ar putea da elevilor plictisiţi, înfrăţiţi doar cu jocurile de pe tabletă sau smartphone.

Am preluat integral, inclusiv titlul, articolul de mai sus din ziarul Magazin, Nr. 52 din 29 dec. 2016, pag. 12, pentru că pur şi simplu merită, reprezentând o pledoarie deosebită pentru o matematică de suflet. Titlul este de-a dreptul magnific. Articolul nu este semnat, doresc însă cu drag să felicit autorul pledoariei respective. Merită să zăbovim un pic asupra conţinutului.

În primul rând, să spunem câte ceva despre “sursa” celor patru seturi de “exerciţii”. Acestea sunt foarte vechi, fiind oarecum din repertoriul universal. Apar împreună sau doar unele în diferite cărţi, dar le putem găsi şi în diferite locuri pe internet. Într-o vreme umbla un Power Point pe e-mail, în care acestea aveau prin prezentare “ataşată” o aură mistică (în 2011, exact aceleaşi patru seturi cu titlul Frumuseţea matematicii).

Apoi, ar trebui să vorbim şi despre momentul cel mai potrivit de folosire al acestora. Părerea mea este că şi-ar găsi locul pe prima fişa de lucru dată elevilor la începutul clasei a V-a, cu cerinţa ca fiecare elev să verifice cât mai multe nivele din fiecare exemplu. Elevii slabi vor face doar câte 2-3 din fiecare; elevii harnici vor face seturile complete. Mesajul este însă unul clar: matematica este frumoasă, dar nu este grea; fiecare poate să facă după forţele sale câte ceva. În plus, aceste exerciţii reprezintă o recapitulare minunată a înmulţirii şi a adunării, fără a fi plictisitoare, ci având chiar o doză bună de “joc”. Este evident că o astfel de fişă poate fi dată doar dacă 1) profesorul de matematică nu consideră că este “sub demnitatea sa”; 2) învăţătoarea nu lea dat deja clasei respective.

Într-un an scurt, cu 365 zile, sunt 52 de săptămâni şi încă o zi (365 : 7 = 52 rest 1). Dacă ne gândim, de pildă la data de 1 ianuarie care poate să fie într-una din cele şapte zile ale săptămânii, observăm că există exact şapte variante de calendar scurt. Astfel, datorită faptului că avem o zi în plus faţă de cele 52 de săptămâni exacte, într-o succesiune de 2-3 ani scurţi ziua de 1 ianuarie va evolua în 2-3 zile ale săptămânii succesive.

Dacă am avea numai ani scurţi de 365 zile, atunci am avea doar şapte forme de calendar care s-ar rula la rând, după care ar lua-o de la capăt, astfel încât prima zi din an s-ar plimba la rând prin zilele săptămânii (L, Ma, Mi, J, V, S, D).

Într-un an bisect, pe lângă cele 52 de săptămâni întregi mai rămân 2 zile rest. Astfel, deducem şi în acest caz două concluzii: 1) există exact şapte calendare posibile de ani bisecţi; 2) dacă am avea doi ani bisecţi în ani succesivi, atunci o zi din calendar, de pildă 1 ianuarie, s-ar muta în săptămână peste două zile.

Dacă am avea dimpotrivă numai ani bisecţi de 366 zile, atunci am avea iarăşi doar şapte forme de calendar care s-ar rula la rând, dar în acest caz prima zi din an s-ar plimba la prin zilele săptămânii sărind peste câte una (L, Mi, V, D, Ma, J, S).

În realitate,după cum se ştie, pe un interval lung de timp avem câte trei ani scurţi intercalati cu unul bisect. În concluzie, prima zi din an se plimbă prin schema săptămânii după un model de tipul (L, Ma, Mi, V, S, D, Ma, Mi, J, S etc.), caracterizabil ca număr de paşi şi prin modelul de periodicitate (1, 1, 1, 2).

Astfel, concluzionăm că există şapte calendare posibile de ani scurţi (cu 365 zile) şi şapte calendare de ani bisecţi (cu 366 zile), ani ce trebuie să umple un interval de periodicitate de 28 de ani, despre care am amintit în prima parte a acestui eseu. Întrebarea este: cum se umple un interval de 28 de ani cu doar 7 + 7 = 14 modele de calendar? Pentru a uşura munca eu am notat cele 14 variante de calendar astfel: a, b, c, d, e, f, g  pentru cei şapte ani simpli (de 365 zile) posibili, respectiv A, B, C, D, E, F, G pentru cei şapte ani bisecţi posibili, notaţi în ordinea în care acestea s-ar succede dacă ar fi doar calendare simple, respectiv doar calendare bisecte. Astfel, calendarele a şi A încep lunea, calendarul b începe marţi, dar calendarul B începe miercuri; calendarul c începe miercuri, dar calendarul C începe vineri etc.

Singurul lucru ce mai rămâne de făcut este de a aranja într-o succesiune de 28 de ani cele 14 modele de calendar, urmând ca la al 29-lea an să constatăm repetarea primului calendar ( piece of cake, cum zice englezu’). Dacă nu v-am ameţit de tot şi aţi reuşit să înţelegeti ce am vrut să spun, atunci vă doresc spor la lucru şi succes în găsirea rezolvării. Dacă însă nu vă descurcaţi, vă rog să nu disperaţi; peste două săptămâni revin cu rezolvarea completă, aşa cum am găsit-o eu.

C.Titus Grigorovici

 

Se poate explica foarte uşor că orice calendar se repetă o dată la 28 de ani. După cum am mai spus, anul acesta – 2017 – funcţionează pe calendarul din anul de graţie 1989! O explicaţie banală ar fi că 7 ∙ 4 = 28, unde 7 ar reprezenta un ciclu de repetare al calendarelor dacă toţi anii ar fi de 365 zile, iar 4 reprezintă periodicitatea anilor bisecţi.

Această explicaţie superficială nu ne spune însă de ce anul acesta – 2017 – funcţionează şi pe calendarul din 2006! Dacă din 1989 nu prea cred că mai are cineva acasă vreun calendar, şansele cresc însă să mai găsim un calendar din 2006. Eu am găsit unul acasă şi altul la un prieten.

Sper că am reuşit să vă trezesc curiozitatea pentru problema repetării calendarului. Deci, ce se întâmplă acolo, cum se repetă calendarele şi de ce? După ce algoritm secret se repetă calendarul dintr-un an? Aceasta a fost întrebarea ce am purtat-o după mine din 2001, când mi-am dat seama cu părere de rău că prosopul cu un calendar din 1972 imprimat pe el, ce îl folosea maică-mea la bucătărie, primit din Germania, tocmai fusese valabil în 2000 (mai ţineţi minte, Millenium?). Dar întrebarea avea un clenci: simţul matematic îmi spunea că nu există 28 de calendare diferite, ci că într-un interval de 28 de ani mai au loc şi alte repetări, mai ciudate. Mai mult n-am făcut pentru că nici nu prea ştiam de unde să apuc problema. Până în ultima vacanţă de iarnă când, în primele zile ale lui 2017 s-a dezlănţuit furtuna în gândire şi, brusc, am rezolvat problema. Pe lângă bucuria rezolvării, am găsit şi o utilitate deosebită pentru noi, profesorii. Problema aceasta nu seamănă cu nimic din ce facem la clasă, din ce avem în programă sau în culegeri pentru olimpiade sau examene, la nici un nivel. Cu alte cuvinte, nu avem o reţetă pentru rezolvarea acesteia, şi ne aflăm astfel în poziţia elevului ce a primit de la profesor o problemă fără să i se fi dat în prealabil o reţetă de rezolvare.

Haideţi să facem acest experiment: luaţi problema atât cât v-am prezentat-o şi încercaţi să o rezolvaţi, să desluşiţi după ce principii pur matematice se repetă calendarul. Este evident că “nu se pun” rezolvări găsite pe net (oricum, nu prea veţi găsi; eu am căutat în diferite limbi, dar nu am găsit altceva decât tabele cu prezentările repetărilor, fără nici o cât de superficială explicaţie). Ce vă pot asigura este că, în afară de împărţirea cu rest nu avaţi de folosit nimic, doar o doză bună de gândire sănătoasă (nu exclud însă ca totuşi cineva să găsească vreo rezolvare în Z₇). Dar, dacă ar fi să o fac la clasă, nu aş coborî sub clasa a VIII-a decât în cazul unor elevi brilianţi.

Haideţi să facem acest experiment şi să studiem pe noi cum este să stai în faţa unei probleme pentru care nu ai o reţetă de rezolvare. Poate asta ne va ajuta pe unii dintre noi să ne dezvoltăm mai mult empatia faţă de elevi. Vă propun acest experiment ca un preambul la o analiză a împărţirii problemelor de matematică în două mari categorii: cele pentru care rezolvitorul are la dispoziţie o reţetă, un model, şi cele pentru care nu are drumul pregătit cu rezolvări deja învăţate. Eu le numesc pe primele probleme reţetabile iar pe cele din a doua categorie probleme off-road (pentru că drumul rezolvării nu este pregătit, nu este asfaltat).

Pentru cei care acceptă să intre în acest joc, promit că voi reveni peste 2 săptămâni cu eventuale indicaţii ajutătoare, iar peste încă alte două săptămâni cu o rezolvare completă, aşa cum am găsit-o eu.

C. Titus Grigorovici

Teoremă:        Orice calendar se repetă odată la 28 ani.

Demonstraţie:            Temă!

Aplicaţie:        Calendarul 2017 ≡ Calendarul 1989

Profu’ de mate’ la manifestaţie

Eugen Rusu şi Dilema cerşetorului

Dacă tot vorbirăm de curând despre cerşetori, cunoaşteţi Dilema cerşetorului, o problemă legată de mucurile de ţigară? Am auzit-o pe vremuri de la un prieten şi am publicat-o prima dată în caietul de matematică P3NT4GON1A nr 4 (mai 1999). Aceasta este una dintr-e cele mai frumoase probleme de matematică distractivă pe care le cunosc. Iar pe lângă partea de matematică distractivă, are şi un factor educativ foarte ridicat. Trebuie doar precizat – undeva, în timpul rezolvării problemei – că este vorba de mucuri de la ţigări fără filtru (elevii de-acum nu prea mai ştiu de-aşa ceva); iar aceasta creşte factorul de scârbire a elevilor faţă de fumat. Deci, iată problema:

Un cerşetor reuşeşte să facă o ţigară întregă din trei mucuri găsite aruncate pe stradă. Câte ţigări va fuma un cerşetor care a adunat zece mucuri?

Nu vă repeziţi să răspundeţi trei ţigări. Întrebarea este despre câte ţigări va fuma, nu despre câte va asambla din cele zece mucuri. Aici este prima capcană a acestei minunate probleme.

*

În acest moment, tocmai ne-am lovit de una din cele mai mari dileme ale publicării problemelor de matematică: Să dau răspunsul final, sau să vă las să savuraţi căutarea acestuia? Dacă vă dau răspunsul, atunci nu veţi parcurge minunatul drum de strădanie, plin de zbucium interior, care duce la descoperirea personală a soluţiei. Acest drum poate să dureze uneori chiar şi zile întregi, inclusiv nopţile dintre ele. În această căutare constă chiar farmecul principal al matematicii.

Când dau astfel de probleme elevilor, rezolvarea are loc într-un dialog. Elevul se gândeşte dar, în cazul în care nu găseşte soluţia corectă, eu îi mai pun o întrebare ajutătoare. Uneori, după întrebarea ajutătoare, îi las pe elevi din nou o zi-două. Apoi reluăm procesul. Aceasta se poate însă doar într-un dialog, chiar şi dacă dialogul este în scris, între două persoane aflate la distanţă. Dar trebuie să fie un dialog.

Pe vremuri, marii matematicieni se provocau astfel prin scrisori cu probleme sau rezolvări găsite personal. Cazul lui Fermat este arhicunoscut, dar şi Arhimede a practicat informarea prin scrisori asupra rezultatelor sale.

Autorii de cărţi cu matematică distractivă dau răspunsurile în partea a doua, la soluţii, mizând pe faptul că cititorul are voinţă şi nu se duce direct la răspuns. De fapt această metodă este folosită la majoritatea culegerilor de matematică. Actualmente, la unele culegeri partea de răspunsuri este atât de înghesuită încât căutarea soluţiei devine o adevărată provocare. Pe vremuri, Grigore Gheba punea răspunsurile chiar lângă exerciţiu, dar acolo provocarea era să nu greşeşti, nu cum se rezolvă, pentru că rezolvarea o ştiai teoretic de la clasă.

Martin Gardner, pe vremea când publica minunatele sale probleme în Scientific American, dădea soluţia de-abia în numărul următor, lăsând astfel cititorilor timp de o lună pentru căutarea soluţiei.

La publicarea unei cărţi, însă, acest dialog de care vorbim este imposibil. El poate fi eventual mimat de către autor prin cei doi paşi (punerea problemei, respectiv oferirea răspunsului), dar realitatea arată că cititorul fuge tot mai das direct la răspunsuri. În acest sens, Eugen Rusu în lucrarea Cum gîndim şi rezolvăm 200 de probleme (Ed. Albatros, 1972), pune chiar mai multe “filtre protectoare” în acest proces în care rezolvitorul este tentat să caute soluţia gratuit. Astfel, lucrarea sa are cinci părţi, concepute pentru a forţa rezolvitorul să caute el singur soluţia. Pentru a da un impuls unei astfel de preocupări, culegerea  nu are numai două părţi, ci patru:

1 ENUNŢURI,   2 CUM GÎNDIM,   3 IDEEA  şi   4 SOLUŢIA
Citește întreg articolul

Discutând prin primăvară cu elevii de clasa a VIII-a, am concluzionat că matematica distractivă este atunci când Profu’ se distrează de elevi, că ei nu ştiu problema :-).

De curând petreceam o Duminică dimineaţă însorită în compania unei ceşti de cafea, lecturând nişte vechi caiete de Gazeta Matematică din 1966-1967 (de când am venit noi pe lume), căutând probleme de folosit la clasă. Vecinul ne tot bâzâia să-i dăm probleme de matematică “din-alea faine”, iar noi îi tot propuneam câte o problemă de matematică distractivă. Când o termina, mai cerea, iar tot anturajul se distra de bucuria sa. În aceste condiţii am găsit în GM seria B, Nr.1 din 1967 următoarea problemă dintr-un set cu titlul Probleme date la Olimpiada matematică din Anglia (problema 7916):

O sută de studenţi de înălţimi diferite sînt aranjaţi într-un pătrat de 10 rînduri şi 10 coloane. În fiecare rând studentul cel mai înalt este selectat, apoi studentul cel mai scund din cei selectaţi este marcat cu A. În fiecare coloană este selectat studentul cel mai scund, apoi studentul cel mai înalt dintre cei 10 studenţi selectaţi este marcat cu B. Dacă A şi B sînt persoane diferite, găsiţi care dintre ele este mai înaltă şi de ce?

Ne-am tot gândit, el a reuşit o rezolvare într-un caz particular, dar nimic mai mult. Apoi, rezolvarea mi-a venit în minte în vis, în somnul binemeritat de după-amiază (vis cu un mic iz de coşmar, pentru că tot pierdeam numărătoarea coloanelor). Când m-am trezit am aşterut rezolvarea pe hârtie, cu desenul celor 100 de studenţi ca o tablă de şah de 10×10, şi am realizat cât este de simplă problema noastră. Dar, de fapt, aşa sunt toate problemele de matematică distractivă: simple, dar cu rezolvarea bine ascunsă.

Titus Grigorovici

Operaţii cu fracţii ordinare şi fracţii zecimale finite

Profesorul Grigore Gheba a publicat în România în anii ’60-’70 o culegere reluată în multe ediţii, ce a ajuns la nivel de cult în învăţarea matematicii. Astfel, majoritatea părinţilor elevilor actuali îşi aduc aminte cu veneraţie de culegerile lui Gheba.

Din multele exemplare ce le-am avut în casă (un raft întreg cu toate ediţiile), ne-au mai rămas în principal două exemplare: cel al soţiei (din 1969) pe care lucraseră înaintea ei şi cei doi fraţi mai în vârstă, cât şi exemplarul meu în limba germană (din 1973), din care a lucrat şi fratele meu. Ambele au fost atât de “muncite”, mai ales în partea cu operaţii cu fracţii suprapuse (numere raţionale), încât primele zeci de pagini sunt distruse, detaşate, de-a dreptul rufoase. Se vede de departe cât de mult s-a lucrat din ele!

Pentru cei care doresc să dea elevilor acele exerciţii “de aur” pentru stabilizarea calculului cu fracţii, vă oferim o variantă a acestora, adaptată la programa actuală a clasei a VI-a, adică fără radicali. Eu, de pildă, le dau elevilor ca temă de lucru în vacanţa de vară, câte una pe zi, 20 la începutul vacanţei şi restul la sfârşit, pentru reamintire.

Titus Grigorovici

Omagiu-Gheba-1.pdf