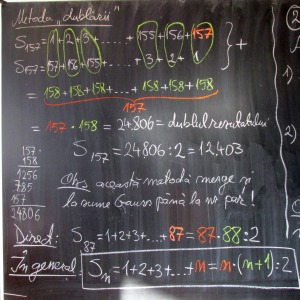Pentagonia

A doua zi după ce D-na Viorica Dăncilă dat renumitul r² ca răspuns pentru aria cercului, Dl Moise Guran a prezentat în Pastila BiziDay un comentariul cu titlul: Ciudatul mod în care Dăncilă le-a fost multora mai utilă decât anii de şcoală …, Rar mi-a fost dat să aud o analiză atât de profundă a situaţiei predării matematicii din şcolile româneşti, ca în acest eseu. În ultima parte a eseului Moise Guran spune următoarele:

*

Se poate învăţa ca pe apă matematica? Este aceasta o ştiinţă ce poate fi tocită, cum se spune? Da, bineînţeles! La nivel de Examen de Capacitate şi de Bacalaureat, da, dar la acest nivel matematica îşi pierde sensul ei adevărat. Devine doar un şir de formule memorate şi utilizate în exersarea unor tipologii de probleme de examen, la fel cam cum au făcut trainer-ii de campanie cu Doamna Dăncilă: x posibile întrebări pentru care pregătim candidatul cu y variante de răspuns, pe care acesta le memorează şi le livrează precum în schiţa cu crastravetele: “ce este elipsa? Păi, nu e clar că tot un fel de crastravete!”

Râdem. Râdem de mai bine de o sută de ani de crastravete, dar de fapt nu ştim nici noi de ce râdem, căci nu copilul care învaţă mecanic poezia e problema, ci profesorul, dascălul, cel care crede că aria cercului trebuie memorată ca o poezie uşoară, când de fapt misterul cercului este chiar afurisitul de pi. Ce este pi? He he, ha ha ha!

Adevărata întrebare este câtora dintre noi ni s-a explicat la şcoală că nu o constantă cu nume grecesc determină cercul, ci din contră, cercul este cel care îl determină pe acest afurisit de pi, infinit în zecimale. Cum se face că toate, dar chiar toate triunghiurile, indiferent că sunt mai mari sau mai mici, indiferent de formă, răspund cu exactitate înmulţirii dintre bază şi înălţime supra doi? Dar de ce nu supra trei sau supra patru? De ce exact supra doi? Vedeţi, acestea sunt întrebări care dau sensul şi scopul matematicii, căci ele, întrebările şi demonstraţia unei formule, iar nu memorarea ei mecanică, ajută un copil să-şi dezvolte logica, inteligenţa, iar mai târziu, când mai creşte şi ajunge adolescent nebunatic, să vadă într-un pahar de bere un cilindru, al cărui volum poate fi calculat pentru că are baza unei forme de cerc.

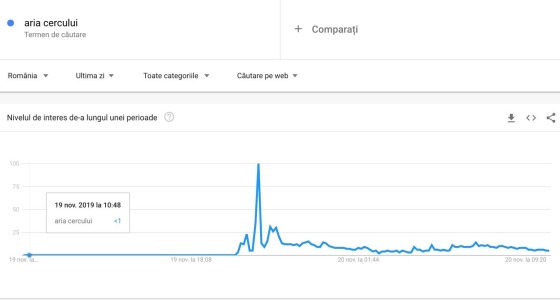
Eşecul Doamnei Dăncilă de a răspunde corect la întrebarea “care este aria cercului?” nu demonstrează în mod necesar că aceasta nu ştie matematică, căci o formulă – fie ea şi cea mai simplă formulă – poate fi uitată. Dar momentul mărturiseşte mult, dureros de mult, despre eşecul sistemului de educaţie românesc în general, de ieri şi de azi, căci Doamna Dăncilă nu doar că şi-a tocit diplomele pe vremea comunismului, dar a predat tehnologie la şcoală de stat şi matematică în privat unor copii de azi, pe care i-a pus să memoreze mecanic formule, sisteme, modele de întrebare şi modele de răspuns, un sistem educaţional care a ajuns atât de jos, încât cel mai mare bine pentru beneficiarii săi pare a fi făcut tot Doamna Dăncilă. Uite, judecând după căutările de pe internet, dar şi după râsetele colective de acum, azi probabil ştiu de zece ori mai mulţi români cum se calculează aria cercului, decât ştiau ieri.

*

Da, dl. Moise Guran surprinde în aceste rânduri esenţa predării matematicii în şcoli, reuşeşte să atingă dincolo de orice dubiu marile întrebări şi dileme ale predării matematicii (atât de mari încât profesorii nici măcar nu le mai văd în zdroaba lor zilnică la catedră). Aproape că am impresia că dânsul i-a citit pe George Pólya sau pe Eugen Rusu. Să reluăm analiza ideilor exprimate. Gândul central al acestor rânduri îl reprezintă opoziţia dintre înţelegerea unei idei din matematică şi învăţarea ei pe de rost (în cazul de faţă aria cercului, dar se poate discuta despre orice alt element de matematică, iar Moise Guran ia repede spre exemplificare şi aria triunghiului). Ce interesantă ar fi o emisiune “Avocatul Diavolului” în care ascultătorii să fie chemaţi a dezbate cu argumente dilema între cele două păreri: “de ce trebuie învăţată matematica pe de rost” şi “de ce matematica trebuie înţeleasă”! Realitatea este că matematica cu greu poate trăi în mintea unui om fără oricare dintre aceste două componente.

Marea problemă a matematicii şcolare româneşti este că există cu duiumul dascăli care consideră că se poate atinge un nivel bun de matematică doar cu învăţarea pe de rost şi fără înţelegerea unui fenomen. Asta datorită faptului că învăţarea pe de rost este mult mai lesne de verificat decât înţelegerea. Primul pas greşit în acest sens îl fac desigur învăţătoarele, care oricum nu sunt setate spre o prea profundă poziţionare înspre înţelegerea matematicii, dânsele confundând în general gândirea unui fenomen cu învăţarea pe de rost a unei reţete de rezolvare. Mult mai dureros este că întâlnim profesori de matematică de liceu care cer învăţarea pe de rost a rezolvărilor exerciţiilor predate chiar şi la clase de mate-info. Cum s-a ajuns la această situaţie? Eu consider că am vreo câteva explicaţii.

În primul rând, datorită faptului că învăţarea pe de rost a unei probleme (de către elevi capabili şi antrenaţi în acest sens) este mult mai lesniceoasă decât formarea gândirii, care este o mare consumatoare de timp. Or, datorită creşterii exponenţiale a cantităţii de tipuri de probleme cu care se confruntă profesorul şi elevii spre excelenţă, tot mai mulţi ajung la ideea că cel mai bine este să înveţi pe de rost că, de verificat te verifică dacă le poţi rezolva, nu dacă le-ai înţeles.

De aici ajungem la a doua cauză: forma problemelor date la examen, chiar şi la olimpiade. Există probleme la modă, cu şanse mari de a fi date, profesorul îi cere să le înveţe (adică să le ştie) iar elevul înţelege că este suficient să le înveţe rezolvările. Există elevi care le ştiu printr-o combinaţe de gândire şi repetiţie, dar există şi mulţi elevi care le învaţă pur şi simplu pe de rost. Odată deschisă această posibilitate pe creierul elevului, acesta va merge tot mai des pe calea învăţării rezolvării (asta se consideră a fi de fapt pregătirea pentru examinarea la matematică), începând tot mai clar să neglijeze înţelegerea fenomenului.

Dar, dacă gândirea şi înţelegerea reală a fenomenului nu se cer la examen, de ce ar mai trebui formată gândirea? Refuz să intru într-o dezbatere a acestei întrebări! Cine nu este în stare să dezvolte un răspuns coerent la această întrebare, acela este deja demn de milă (din punctul meu de vedere). Mai degrabă m-aş ocupa de întrebarea – pe care Moise o atinge doar tangenţial, anume când ar trebui să ne ocupăm de formarea gândirii, de vreme ce cea mai mare parte a timpului orelor de matematică se desfăşoară sub spectrul pregătirii examenului. În diversele mele articole am încerca să dau un răspuns la această întrebare, şi anume că avem datoria să ne ocupăm de formarea gândirii raţional-logice deductiv-argumentative, dar şi că putem face aceasta foarte bine în cadul introducerii noilor noţiuni şi cunoştinţe. Cu alte cuvinte, dezvoltarea gândirii se poate face eficient îndrumând elevul spre cunoaşterea fiecărui pas din matematică pe o cale similară cu cea pe care a fost descoperit pasul respectiv, adică refăcând traseul de gândire urmat de descoperitorul acelui pas.

Eu folosesc pentru descrirea acestei căi denumirea de “predare prin problematizare”. Aceasta însă nu poate fi aplicată la ora actuală din două mari motive. Întâi că este mare consumatoare de timp şi ar trebui să i se facă loc în timpul orelor de matematică (ghici ce componentă a orelor de matematică ar trebui restrânsă, adică unde ar trebui să scadă pretenţiile?). Apoi, din punct de vedere a pregătirii metodico-didactice a profesorilor de matematică, predarea prin problematizare nu a fost şcolită deloc în cea mai mare parte a facultăţilor, profesorii neînţelegând ce ar trebui să facă, metoda fiind cvasi-dispărută din mentalul breslei noastre (de aia mă agit atâta, pentru că am impresia că sunt printre ultimii, dacă nu chiar ultimul, care mai ştiu câte ceva despre asta).

Pe lângă aceste două aspecte ce ţin de profesori, mai există şi unul colateral, ce ţine de elevi. Se poate face predarea prin problematizare la orice elev care colaborează şi nu închide poarta gândirii, preocupându-se la oră doar să scrie de pe tablă, cel mai bine rămânând chiar puţin în urmă, asigurându-şi astfel o preocupare “serioasă” pentru momentele când profesorul le cere elevilor să lucreze ceva independent (dar, copiez).

Toate aceste aspecte ar trebui să facă subiectul unei preocupări intense din partea conducătorilor matematicii şcolare româneşti. Institutul de ştiinţe a educaţiei ar trebui să fie centrul acestei preocupări de “desţelenire” a respectivului teritoriu al cunoaşterii demult uitat, dar intens studiat şi analizat în anii ’60-’70 de Polya la nivel mondial, dar şi la noi prin Profesori Eugen Rusu, A. Hollinger ş.a. (Universitatea din Bucureşti a avut până prin anii ’90 demni continuatori ai acestor doi metodişti legendari şi sigur se poate reînoda tradiţia acelei forme de pregătire a profesorilor).

Ultimele gânduri – cele legate de pregătirii metodico-didactice a profesorilor – reprezintă oarecum o a treia cauză a supraevaluării ideii de învăţare pe de rost. Obsesia teoreticistă introdusă în cadrul reformei “din 1980” (reforma uitată ce s-a pornit prin 1977 şi a ajuns la apogeu prin 1981), cu care a fost bombardaţi profesorii în anii ’80, a ajuns să fie acceptată şi însuşită ca paradigmă de marea masă a profesorilor în anii ’90, iar acum colegii nu înţeleg cu ce greşesc, pentru că ei aşa sunt setaţi. Or, o schimbare de paradigmă la nivelul predării necesită mult mai mult decât câteva pagini explicative în jurul unei noi programe (vezi programa de gimnaziu din 2017).

Cu alte cuvinte, este mult mai uşor să dictezi simplu o definiţie, decât să te chinui să formezi intuitiv, prin gândire, respectiva noţiune. De fapt greşesc prin această afirmaţie, pentru că starea de fapt este mult mai dramatică: oare, câţi profesori îşi pun măcar întrebarea că ar putea introduce o noţiune altfel decât dând o definiţie sau o explicaţie?

Revenind la dezvoltarea gândirii prin problematizare, desigur că gândirea poate fi dezvoltată şi prin problematizarea simplă, adică prin problematizare în rezolvarea unei probleme. Nu este neapărat să o faci doar în cazul predării, adică a introducerii noţiunilor noi, şi chiar este de dorit să o faci şi în cazul problemelor (de reţinut desigur că şi în acest caz devine consumatoare de timp). “Problema este că” în mentalul elevilor lecţiile sunt oarecum mai importante decât problemele (şi Moise Guran sugerează asta prin discursul său), aşa că sunt şanse crescute să fie mai atenţi şi mai colaborativi la lecţie decât la probleme: poate că elevul a auzit despre radicali şi este curios cum sunt aceştia (deşi şi problemele au argumentele lor: “pot veni la test”).

Moise Guran atinge în discursul său şi un alt punct important: faptul că matematica îi poate atrage pe elev spre gândire prin declanşarea fenomenului de uimire. Din păcate şi acest proces al mirării urmat de dorinţa de a găsi un răspuns “că de ce se întâmplă aşa”, şi acest proces este unul mare consumator de timp. Dar predarea teoreticist definiţionistă practicată în ultimii 30 de ani ca politică oficială în nici un caz nu poate stârni gânduri de uimire. Uimirea apare în matematică atunci când este descoperit un fenomen nou, iar nu când vine un profesor şi-ţi expune în stil plat-academic a succesiune de definiţii, observaţii şi teoreme, pe un ton monoton. Uimirea a avut loc atunci când un matematician a descoperit ceva. Dimpotrivă, uimirea a fost eliminată, desfiinţată atunci când un profesor universitar a prelucrat acele idei şi le-a organizat într-o formă corect-demonstrativ teoretică. Dacă la nivel academic acest proces îşi găseşte justificarea prin ordonarea teoretică a matematicii, introducerea absolutizată a acestui stil de predare la nivel preuniversitar a distrus încetul cu încetul formarea gândirii la elevi. Deci, elevului trebuie să i se permită parcurgerea de paşi de descoperire similari cu cei parcurşi de descoperitorii matematicii, iar asta cât mai des posibil. Aceşti paşi sunt cei formatori de gândire şi nu “turnarea cu tolcerul” (cu pâlnia) a lecţiilor în capul elevului, oricât de riguroasă ar fi aceasta.

Elevul trebuie să se poată lupta cu înţelegerea fenomenului de pi măcar o vreme, aşa cum omenirea s-a luptat secole, chiar milenii cu acest proces. Materia şi lecţiile trebuie astfel aranjate încât elevul să facă pasul de judecată pentru înţelegerea cauzei formulei ariei triunghiului, înainte de învăţarea formulei respective pe de rost. Dimpotrivă, predarea ariei triunghiului printr-o definiţie, aşa cum se putea găsi într-un manual “alternativ” din 1997, această formă de predare a fost una anihilatoare de gândire, prin definire omorându-se de fapt din faşă orice tentativă a întrebării “de ce?”, întrebare ce reprezintă sămânţa gândirii.

Este evident că acest subiect merită continuat şi analizat şi răs-analizat, dar cred că este suficient pentru această a treia parte a eseului de analiză pastilei BiziDay din 20 noiembrie. În vacanţă mă voi concentra pe o altă cauză – una năucitoare – a faptului că evaluarea prea agresivă este în sine anihilatoare de gândire, fiind una din cauzele eşecului sistemului de educaţie românesc în general, de ieri şi de azi. Nu închei însă înainte de a atrage atenţia asupra felului deosebit de organic în care se leagă textul lui Moise Guran de ştirea despre “eşecul” învăţământului românesc la Studiul PISA, ştire ce avea să pice peste nici două săptămâni. CTG

Parafrazând un vechi cântec reluat prin anii ’90 (Alice, who … is Alice), putem întreba pe bună dreptate: PISA, ce-i aia PISA? Am gasit pe HotNews.ro câteva elemente sugestive şi câteva explicaţii destul de clare pe care le-aş relua şi le-aş suplimenta cu anumite comentarii (vezi întregul material la https://www.hotnews.ro/stiri-educatie-23528977-rezultate-pisa-2018-performante-slabe-ale-elevilor-romani-cel-mai-mic-punctaj-din-2012-pana-acum.htm).

PISA este prescurtarea pentru Programme for International Student Assessment (în traducere Programul pentru Evaluarea Internaţională a Elevilor) şi este o testare care se desfăşoară o dată la 3 ani şi arată nivelul elevilor de 15-16 ani la matematică, ştiinţă şi citire.
PISA evaluează măsura în care elevii au dobândit cunoştinţe şi abilităţi esenţiale pentru participarea deplină la viaţa socială şi economică. Evaluările PISA nu caută să vadă doar dacă elevii care se află la sfârşitul învăţământului obligatoriu pot reproduce ceea ce au învăţat, ci examinează cât de bine pot ei extrapola din ceea ce au învăţat şi dacă îşi pot aplica cunoştinţele în situaţii necunoscute, atât în şcoală cât şi în afara acesteia.

Studiul PISA este realizat de Organizaţia pentru Cooperare şi Dezvoltare Economică (OECD) şi are în vizor toată populaţia şcolară, dorind să ofere o imagine a generaţiei respective asupra abilităţii acestora de integrare în viaţa activă a societăţii peste numai câţiva ani. La fel ca şi sondajele de opinie în vederea alegerilor, şi studiul PISA se desfăşoară pe eşantioane alese astfel încât să fie reprezentative pentru întreaga populaţie şcolară a unei ţări. Cu alte cuvinte, rezultatele unui astfel de studiu s-ar schimba dramatic dacă s-ar alege eşantioane favorabile, în conformitate cu curentul de mândrie naţională despre „olimpicii noştrii”, curent rămas oficial şi după 1989 (reamintesc că acest curent de opinie a fost impus de Ceauşescu în anii ’80 când am auzit 10 ani despre “societatea multilateral dezvoltată” şi despre “omul de tip nou”). O astfel de alegere însă şi-ar pierde relevanţa pentru societatea românească.

Din păcate – din cauza lipsei unei analize realiste a stării ideologice a societăţii noastre – România a făcut în toţi aceşti 30 de ani şi în educaţie doar jumătate de pas înspre o schimbare reală şi sănătoasă, la fel ca în orice domeniu de altfel (spre exemplificare: vrem calitate de maşini nemţeşti de elită, strâmbând din nas la orice nu este top, dar când producem noi ceva, cei mai mulţi suntem dominaţi în continuare de “merge şi-aşa!” sau de renumitul “da’ ce-are!” când ne este reclamată o deficienţă a rezultatului muncii noastre). Aşadar, la fel ca în orice domeniu şi în cazul educaţiei apare respectiva schizofrenie: comandăm ca ţară studiul PISA şi plătim pentru asta peste 150.000 de euro, după care vine D-na proaspăt Ministru Monica Anisie şi declară că “nu trebuie neapărat să ne îngrijoreze, pentru că accentul nu se pune neapărat pe ce ştiu elevii, ci pe ce aplică”. În matematică folosim q.e.d.: adică, DA, noi ştim că o foarte mare parte din populaţia ţării este neglijată cu totul de către politica educaţională a statului român, dar ce mândri suntem de restul, de “olimpicii noştri” şi de toţi cei care învaţă bine în clasele şi în şcolile noastre bune şi care apoi aplică la şcoli înalte din străinătate (ultimul m-a anunţat aseară că va aplica la o facultate din Scoţia) şi apoi devin “Ăştia” şi veci nu se mai întorc (“citat” pamfletar printre rânduri!). Da, aşa se înţeleg D-nă Ministru, vorbele dvs. Şi când te gândeşti că era atât de simplu să fiţi cinstită şi să daţi pur şi simplu vina pe cei dinaintea dvs. Sau, poate, chiar aţi fost cinstită în sinea dvs., şi de fapt aşa gândiţi. Atunci înseamnă că a avut dreptate Moise Guran cu desfiinţarea inspectoratelor şcolare.

Aşadar, facem o testare despre întregul spectru de elevi, dar nu ne interesează ce ne spune aceasta despre CE se pricep să aplice, sau mai exact să nu aplice, după ani buni de şcoală aproape jumătate din populaţia şcolară. “Ei ştiu de altfel foarte multe lucruri după toţi aceşti ani de şcoală, dar nu ştiu să le aplice”. Asta sună cam ca aia din 2008 a D-lui Tăriceanu, că economia românească duduie, iar criza mondială n-are cum să ne îngrijoreze.

Cu alte cuvinte fiind spus – şi acest aspect nu l-am regăsit în nici măcar o luare de poziţie – Studiul PISA oferă o imagine a învăţământului nostru opusă structural imaginilor tradiţional măgulitoare oferite de sistemul elitist, în sensul că ne atrage atenţia şi asupra celeilalte părţi a populaţiei şcolare, asupra celor slabi la matematică (deşi nici imaginile oferite de sistemul elitist olimpic nu mai sunt ce-au fost altădată, decăzând la rând cu celelalte domenii gândite de Ceauşescu pentru a ne convinge de eficienţa politicii sale, cum ar fi Naţionala de fotbal sau gimnastica – la Olimiada de la Tokyo nici măcar nu vom mai fi reprezentaţi de echipa de gimnastică, iar exemplele pot continua mult şi bine). Pe când rezultatele elitiste ne oferă o imagine luminoasă, Studiul PISA integrează în tablou şi partea neglijată a populaţiei şcolare, iar faptul că această parte neglijată creşte de la un Studiu PISA la următorul, această stare de lucruri ar trebui să ne îngrijoreze!

Totul revine însă la o altă paradigmă groaznică ce ne conduce mental activitatea: pentru ce învăţăm de pildă matematica? Pentru examene (obligatoriu) şi pentru concursuri (cei mai buni). Păi da, şi atunci cei care nu dau examene, cu aceştia ce facem? Păi, aceştia pot să rămână analfabeţi funcţionali în matematică! Situaţia lor “matematică” nu ne interesează. Da, cam aceasta este atitudinea societăţii despre matematică şi cei care nu o ştiu. Toţi elevii care nu învaţă şi nu ştiu matematică, chiar şi la un nivel minimal, toţi aceştia nu vor trage deloc foloase din capacitatea formatoare a matematicii înspre dezvoltarea unei gândiri raţionale şi logice. Cu alte cuvinte, toţi cei 47% dintre elevi români care nu au atins măcar nivelul 2 din studiul PISA, toţi aceştia pot fi clasificaţi drept analfabeţi funcţional din punct de vedere al gândirii raţional logice. Mai exact, aceşti elevi nu pot interpreta şi recunoaşte, fără instrucţiuni directe, modul în care o situaţie simplă poate fi reprezentată matematic, cum ar fi de exemplu, compararea distanţei totale pe două rute alternative sau convertirea preţurilor într-o monedă diferită.

Mai mult, chiar şi dacă aceştia reuşesc să identifice reţeta de aplicat (dintre cele învăţate la clasă) şi o şi aplică, ei nu sunt în stare să-şi recunoască validitatea sau falsitatea răspunsului dat. De pildă, am dat în finalul lui noiembrie la clasa a VII-a următoarea problemuţă: Ducem la curăţătorie un covor rotund cu diametrul de 2,80 m. Stabiliţi câţi m² are acest covor (formulă şi calcul cu două zecimale exacte). Dintre cei care au ştiut să identifice că trebuie să calculeze aria (deşi nu era precizat concret cuvântul arie) şi au pus corect formula (mulţumim D-na Viorica!), dintre aceştia au fost totuşi foarte mulţi care n-au pus la rezultat virgula unde trebuie (inclusiv unii care n-au pus-o deloc). Aceştia nu şi-au dat seama că un astfel de covor nu poate avea 60 m² sau chiar 600 m². Pentru ei aceste numere nu au o însemnătate clară, pentru ei acestea sunt doar „numere” (şi matematica lucrează cu numere că aşa vrea ea). Întrebarea „oare mi-a dat corect” nu este acoperită de vreun fel de gândire (cred că în mintea unora rezultatele problemelor de matematică au un statut similar cu datul cu zarul: la ambele e vorba de numere şi apoi „om vedea ce iese”). Probabil că peste ani, într-o situaţie de calcul a preţului la o curăţătorie de covoare, ei îşi vor da seama că ceva nu e bine, dar acum „li se rupe-n 14”.

Aceste gânduri ne duc mai departe şi la o altă întrebare despre care încă n-am auzit o analiză realistă: Cine-i de vină? Există articole care vorbesc despre vina sistemului sau despre vina profesorilor, despre lipsa manualelor, despre planul cadru sau despre programe; dar cine-i bagă în seamă pe toţi aceştia care aparent doar dau cu părerea? Chiar şi reprezentanţii Consiliului naţional al elevilor au ieşit la declaraţii: ei consideră că planul cadru şi metodele de predare ar fi de vină şi serios că nu-i pot contrazice.

Pe de altă parte există articole care vorbesc despre vina părinţilor; mai puţine însă vorbesc şi despre vina atitudinii elevilor. Nu vorbeşte însă nimeni despre cauzele acestora şi, mai ales, nu li se explică părinţilor despre urmările în ne-dezvoltarea atenţiei şi a capacităţilor de gândire, despre urmările extinderii folosirii excesive a ecranelor la nivel naţional, prin reţelele ce oferă pachete de televiziune prin satelit în fiecare locuinţă (până şi în ultima cocioabă conectată la reţeaua electrică), dar şi despre urmările accesul nelimitat la internet prin telefoanele inteligente (2007 primul i-phone, după 2010 încet dar sigur la tot mai mulţi copii de vârste tot mai fragede petrecând tot mai mult timp în faţa ecranelor).

Toată această îmbârligătură de vini bănuite sau nebănuite susţine o stare în care oricine poate arăta cu degetul în altă parte, numai la el nu: „Ceilalţi sunt de vină, nu eu!”. De fapt, pe mine personal nici nu mă interesează cine-i de vină, cum nici nu m-ar încălzi cu nimic tragerea la răspundere a vinovaţilor. Singurul lucru cu adevărat important ar fi recunoaşterea completă a situaţiei şi luarea unor decizii de corectură în conformitate cu tabloul complet. Nici măcar nu m-ar interesa de fapt ca acest proces să se desfăşoare la vedere. Ar putea fi foarte bine manager-uit de către o comisie de încredere. Problema este că ne-am cam săturat de atâtea „comisii” care ne duc dintr-o reformă în alta. Vorba lui Tudor Gheorghe: „30 degeaba!”.

P.S. Apoi, ce să mai vorbim despre faptul că la sezonul de alegeri de peste 5 ani, aceşti 47% vor avea drept de vot? Oare, cum se vor putea ei păzi de a nu fi fraieriţi de un partid sau de un candidat anume? UAU! Vremuri grele ne aşteaptă! Oare această stare de fapt a fost intenţionat cauzată, sau „it just hapened”? Hmmm!

A doua zi după ce D-na Viorica Dăncilă a scos perla cu renumitul r² pentru aria cercului, Dl Moise Guran a prezentat în Pastila BiziDay (20 noi. 2019) un comentariul cu titlul: Ciudatul mod în care Dăncilă le-a fost multora mai utilă decât anii de şcoală …, comentariu la adresa evenimentului, dar şi în general la adresa matematicii şi a politicii educaţionale prin care aceasta este introdusă elevilor. Am prezentat în prima parte a acestei serii întregul text, cât şi o primă analiză la adresa pasajului introductiv despre clasica întrebare retorică a elevilor “La ce ne ajută matematica?”. După pasajul introductiv şi scurtul solo la chitară (de origine Iron Maiden), Moise Guran intră direct în profunzimea metodicii predării matematicii:

MG: Deşi formula ariei cercului are o muzicalitate aparte, aşa – pi-er-pătrat – ceea ce e drept o face uşor de confundat cu perimetrul cercului – doi-pi-er – tot e mult mai uşor de reţinut decât oricare altă formulă matematică, de exemplu baza ori înălţimea supra doi, cum ar fi aria afurisitului de triunghi, de exemplu. Sau poate, nu acestea sunt formulele, şi le-aş putea greşi la rândul meu. Nu le-am mai folosit de mult. Cu adevărat greşit însă, în tot ceea ce v-am spus eu, este expresia “uşor de reţinut”. Sunt lucruri pe care le reţinem mecanic pentru că le folosim tot timpul, aşa cum ar fi, în cazul meu, numărul de telefon al nevestei, sau sunt lucruri pe care mu le-am mai folosit de mult şi firesc le uităm pentru a face loc în memorie altor numere de telefon, pinului de la card, parolei contului de facebook sau doar altor informaţii de zi cu zi.

CTG: Da, aici este atinsă exact acea parte de matematică ce trebuie învăţată pe de rost. Nu poţi de fiecare dată să-ţi demonstrezi “again & again” (din nou şi din nou) fiecare formulă. Cele des folosite trebuie şi merită învăţate pe de rost. Unii elevi se împotrivesc şi calculează de fiecare dată cât face pătratul lui 12, până când oricum încep să-l ştie. Aceştia îţi vor explica că se descurcă şi la extragerea radicalului prin descompunere. Pe ei îi vom lămurii că la rădăcina lui 169 sau a lui 289 nu se vor descurca cu descompunere. Pe cei care nu se lasă, îi “bubuim” cu un radical din 361. În urmă cu mulţi ani la o simulare de clasa a 8-a, toată clasa a fost blocată timp de 10 minute din cauza acestuia. La sfârşitul simulării a venit în clasă diriginta, care era profesoară de engleză: “Ei, cum a fost?” a întrebat ea. Când i-am spus că n-au ştiut radical din 361, s-a îndreptat indignată către ei: “Cum? Naţi ştiut că-i 19?” Toată clasa a rămas blocată (ei neştiind că Diriga lor se pregătise pentru matematică până în martie în a 12-a, la rândul ei de dragul dirigintei, care era profesoară de matematică).  Alţii consideră că nu-i nevoie să înveţe pe de rost şi a aplica automat formula (a + b)², încercând de fiecare dată să înmulţească (2x + 7) cu el însuşi, neştiind că astfel nu vor face faţă la lecţia simetrică de descompunere în factori, şi exemplele pot continua mult şi bine.

Da, mulţi elevi se opun învăţării pe de rost, dar nici politica educaţională a matematicii nu-i ajută. Elevii ar trebui să primească suficiente exerciţii elementare care să-i pună în situaţia reţinerii unei formule sau a unor numere speciale pe baza folosirii dese. După 1997 odată cu apariţia manualelor alternative au dispărut din repertoriul de zi cu zi al orelor de matematică şi al temelor aplicaţiile de bază într-o cantitate suficientă încât elevii să memoreze elementele datorită folosirii acestora de multe ori în situaţii elementare. De-abia după acest moment ar fi voie de trecut la aplicaţii mai avansată. Or, dacă studiaţii orice manual sau auxiliar, la momentele de bază cu greu găseşti 2-3 aplicaţii simple. Este mult mai uşor să-i bombardezi din prima cu aplicaţii superioare, iar în paralel să le ceri să înveţe pe de rost orice. Am întâlnit colegă ce predă la o şcoală de elită şi care le cerea elevilor de liceu de la mate-info să înveţe pe de rost şi rezolvările diferitelor exerciţii (adevărate probleme superîmbârligate, numite “exerciţii” doar pentru că nu au un text consictent).

Ce este deci cel mai rău, este că profesorii ajung să absolutizeze ideea învăţării pe de rost (dar nu numai profesorii, ci şi părinţii sau chiar elevii). Chiar şi acest aspect a ajuns să fie atins de Moise Guran ceva mai încolo:

MG: Râdem de mai bine de o sută de ani de crastravete, dar de fapt nu ştim nici noi de ce râdem, căci nu copilul care învaţă mecanic poezia e problema, ci profesorul, dascălul, cel care crede că aria cercului trebuie memorată ca o poezie uşoară …Eşecul Doamnei Dăncilă de a răspunde corect la întrebarea “care este aria cercului?” nu demonstrează în mod necesar că aceasta nu ştie matematică, căci o formulă – fie ea şi cea mai simplă formulă – poate fi uitată.

Aşadar, secretul constă în găsirea liniei juste de departajare între cele de învăţat pe de rost, pe de o parte, cele de gândit pe de altă parte şi cele mediane, acele exerciţii a căror rezolvare devine automată, dar nu se învaţă pe de rost. Însă, despre cele de gândit vom discuta în a treia parte a comentariilor despre această pastilă Biziday. CTG

P.S. Încerc să ţin o ordine a postărilor cât de cât coerentă, dar cu greu fac faţă frecvenţei cu care apar în ultima vreme în viaţa publică evenimente ce au legătură cu predarea matematicii. Eu sunt un simplu profesor, pe lângă ore (ce trebuie pregătite) am şi teste de redactat şi de corectat; apoi am şi o viaţă extramatematică şi nu mai apuc să scriu tot ce ar fi nevoie. Sper să apuc în vacanţă, adică vreau să spun că sper că în vacanţă se vor mai linişti şi nu vor mai apărea evenimente noi de analizat, astfel încât să le pot epuiza pe cele ce s-au îngrămădit în ultima vreme. Oricum , e clar că dacă n-ar fi existat, pentagonia ar fi trebuit inventată. Glumesc desigur, dar în spatele acestei glume se ascunde o situaţie rar întâlnită. Nu ţin minte să mai fi fost o stare atât de evidentă de agitaţie în jurul matematicii şcolare, ca în această perioadă.

A doua zi după ce D-na Viorica Dăncilă “a scos porumbelul pe gură” cu renumitul r² pentru aria cercului, Dl Moise Guran a prezentat în Pastila BiziDay (20 noi. 2019) un comentariu extraordinar la adresa evenimentului, dar şi în general la adresa matematicii şi a politicii educaţionale prin care aceasta este introdusă elevilor. Comentariul din această Pastilă Biziday cu Moise Guran poate fi ascultat la adresa https://www.youtube.com/watch?v=H2s078_RDmY, sub titlul: Ciudatul mod în care Dăncilă le-a fost multora mai utilă decât anii de şcoală … Iată în continuare în text întregul discurs (cu câteva adăugări minore pentru cursivitate şi claritate în lecturare):

*

Acum vreo câţiva ani, pe când era fiu-meu la şcoală, unul dintre puşti a întrebat-o pe profa de mate “la ce ne foloseşte Doamna matematica în viaţă?”. Profesoara s-a cam ofensat şi n-a avut un răspuns foarte concret. Pe vremuri, pe vremuri mai golăneşti aşa, pe când eram eu în liceu iar Revoluţia ne făcuse să credem că democraţia înseamnă să stăm cu profii la fumat şi uneori şi prin baruri, un amic i-a pus aproximativ aceeaşi întrebare profesorului nostru de matematică: “Domnu’, dacă n-ar fi Bacalaureatul iar noi n-am fi la mate-fizică, ne-ar trebui la ceva matematica asta în viaţă?”, iar profesorul nostru de atunci, un gentelman de care îmi amintesc cu plăcere, deşi nu prea mă scotea din 5 şi 6, a zis cam aşa: “Da, tinere domn, ca să ştii şi tu câte pahare poţi să bei înainte să nu te mai poţi ridica de pe scaun”.

Deşi formula ariei cercului are o muzicalitate aparte, aşa – pi-er-pătrat – ceea ce e drept o face uşor de confundat cu perimetrul cercului – doi-pi-er – tot e mult mai uşor de reţinut decât oricare altă formulă matematică, de exemplu baza ori înălţimea supra doi, cum ar fi aria afurisitului de triunghi, de exemplu. Sau poate, nu acestea sunt formulele, şi le-aş putea greşi la rândul meu. Nu le-am mai folosit de mult. Cu adevărat greşit însă, în tot ceea ce v-am spus eu, este expresia “uşor de reţinut”. Sunt lucruri pe care le reţinem mecanic pentru că le folosim tot timpul, aşa cum ar fi, în cazul meu, numărul de telefon al nevestei, sau sunt lucruri pe care mu le-am mai folosit de mult şi firesc le uităm pentru a face loc în memorie altor numere de telefon, pinului de la card, parolei contului de facebook sau doar altor informaţii de zi cu zi.

Se poate învăţa ca pe apă matematica? Este aceasta o ştiinţă ce poate fi tocită, cum se spune? Da, bineînţeles! La nivel de Examen de Capacitate şi de Bacalaureat, da, dar la acest nivel matematica îşi pierde sensul ei adevărat. Devine doar un şir de formule memorate şi utilizate în exersarea unor tipologii de probleme de examen, la fel cam cum au făcut trainer-ii de campanie cu Doamna Dăncilă: x posibile întrebări pentru care pregătim candidatul cu y variante de răspuns, pe care acesta le memorează şi le livrează precum în schiţa cu crastravetele: “ce este elipsa? Păi, nu e clar că tot un fel de crastravete!”

Râdem. Râdem de mai bine de o sută de ani de crastravete, dar de fapt nu ştim nici noi de ce râdem, căci nu copilul care învaţă mecanic poezia e problema, ci profesorul, dascălul, cel care crede că aria cercului trebuie memorată ca o poezie uşoară, când de fapt misterul cercului este chiar afurisitul de pi. Ce este pi? He he, ha ha ha!

Adevărata întrebare este câtora dintre noi ni s-a explicat la şcoală că nu o constantă cu nume grecesc determină cercul, ci din contră, cercul este cel care îl determină pe acest afurisit de pi, infinit în zecimale. Cum se face că toate, dar chiar toate triunghiurile, indiferent că sunt mai mari sau mai mici, indiferent de formă, răspund cu exactitate înmulţirii dintre bază şi înălţime supra doi? Dar de ce nu supra trei sau supra patru? De ce exact supra doi? Vedeţi, acestea sunt întrebări care dau sensul şi scopul matematicii, căci ele, întrebările şi demonstraţia unei formule, iar nu memorarea ei mecanică, ajută un copil să-şi dezvolte logica, inteligenţa, iar mai târziu, când mai creşte şi ajunge adolescent nebunatic, să vadă într-un pahar de bere un cilindru, al cărui volum poate fi calculat pentru că are baza unei forme de cerc.

Eşecul Doamnei Dăncilă de a răspunde corect la întrebarea “care este aria cercului?” nu demonstrează în mod necesar că aceasta nu ştie matematică, căci o formulă – fie ea şi cea mai simplă formulă – poate fi uitată. Dar momentul mărturiseşte mult, dureros de mult, despre eşecul sistemului de educaţie românesc în general, de ieri şi de azi, căci Doamna Dăncilă nu doar că şi-a tocit diplomele pe vremea comunismului, dar a predat tehnologie la şcoală de stat şi matematică în privat unor copii de azi, pe care i-a pus să memoreze mecanic formule, sisteme, modele de întrebare şi modele de răspuns, un sistem educaţional care a ajuns atât de jos, încât cel mai mare bine pentru beneficiarii săi pare a fi făcut tot Doamna Dăncilă. Uite, judecând după căutările de pe internet, dar şi după râsetele colective de acum, azi probabil ştiu de zece ori mai mulţi români cum se calculează aria cercului, decât ştiau ieri. Indiferent că-l văd, sau că nu mai pot să-l vadă pe fundul unui pahar. Momente şi schiţe, aceasta este ţara.

*

Rar mi-a fost dat să aud o descriere atât de profundă a situaţiei predării matematicii din şcolile româneşti, ca în acest eseu. Haideţi să analizăm pentru început pasajul introductiv ce atrage atenţia asupra unei întrebări cu care orice profesor de matematică se confruntă dacă elevii ajung să simtă un oarecare curaj (un ascendent) în faţa sa.

MG: Acum vreo câţiva ani, pe când era fiu-meu la şcoală, unul dintre puşti a întrebat-o pe profa de mate “la ce ne foloseşte Doamna matematica în viaţă?”. Profesoara s-a cam ofensat şi n-a avut un răspuns foarte concret.

CTG: Despre întrebările “La ce foloseşte matematica?” am mai vorbit. Poate merită totuşi accentuat şi aspectul realist ce se ascunde în spatele acestor întrebări. Foarte mulţi (actuali sau foşti elevi) simt într-adevăr că matematica pare să se preocupe mai mult de ea însăşi decât de elevi. Profesorii de matematică sunt de prea multe ori slujbaşi ai matematicii şi nu ai elevilor, aşa cum ar trebui de fapt să fie; sunt slujbaşi ai unei matematici despre care elevii în nici un caz nu simt că le-ar folosi; nu-i văd sensul şi le repugnă.

Desigur că şi elevii greşesc de multe ori atunci când consideră că “cea mai bună matematică este atunci când aceasta lipseşte cu desăvârşire”, dar această părere vine tocmai din faptul că elevul nu înţelege sensul celor ce se întâmplă la ora de matematică. În linii mari sunt trei direcţii în care este impinsă excesiv matematica, direcţii care-i uită pe majoritatea elevilor şi din cauza cărora aceştia se simt neglijaţi (în funcţie de rapiditatea cu care se instalează pubertatea la elevi, aceştia încep să “comenteze”, să pună întrebări de tipul evocat de Moise Guran). Cele trei direcţii care rup matematica de zi cu zi de majoritatea elevilor, respingându-i constant, sunt următoarele: 1) Rigurozitatea în sine a matematicii; 2) Excelenţa (olimpiade şi alte concursuri); 3) “Pregătirea pentru examene”. Să le analizăm pe rând (şi pe scurt, fiecare putând reprezenta în sine subiectul unui eseu extins).

1) Despre rigurozitatea matematicii am tot vorbit: la nivelul şcolar (gimnazial şi liceal) aceasta a fost ridicată la cote greu de suportat pentru elevi în cadrul reformei de la sfârşitul anilor ’70 (vedeţi postările în care am vorbit despre “Reforma uitată”). Rezultatul unor cursuri universitare despre predarea axiomatică au fost turnate mai întâi în liceu, apoi chiar în gimnaziu. Înţelegerea iniţială a matematicii, care trebuie să aibă loc în mod natural pe căi intuitive, a fost eliminată cu totul, elevii fiind puşi în situaţia de a lua contactul cu fenomenele studiate doar la nivel abstract teoretic “axiomatico-definiţionist”. Majoritatea covârşitoare a elevilor nu a înţeles şi nu a făcut faţă noii abordări, dar sistemul – printr-o atitudine de stat poliţienesc – nu a ţinut cont de realitatea din şcoli (timp de un sfert de secol, cam până la începutul anilor 2000). Acum, deşi noua programă de gimnaziu cere o revenire, profesorii la rândul lor nu înţeleg această cerinţă şi nu sunt dispuşi a părăsi “zona de comfort”, mai ales că dinspre “minister” nu vine clar o lămurire despre ce şi cum (nici inspectorii care ar trebui să fie vectorul principal de reformare, nici dânşii nu înţeleg foarte bine ce şi cum).

Abordarea excesiv de riguroasă îi alungă pe majoritatea elevilor, dar elevii se împart în două categorii din acest punct de vedere: a) majoritatea nu o înţeleg, iar pentru aceştia rigurozitatea devine o corvoadă imposibil de dus; b) cei puţini care o înţeleg şi îi fac faţă, o duc cumva, dar îi chinuie şi nu prea pricep la ce le ajută. Chiar şi acestora, de la un anumit nivel în sus rigurozitatea nu le foloseşte la nimic.

2) Preocuparea pentru excelenţă îi alungă pe toţi elevii care nu fac faţă problemelor şi aplicaţiilor mult prea grele pentru pregătirea olimpiadelor. Şcolile sau clasele unde se trage tare pentru excelenţă sunt pline şi de elevi care se chinuie în această atmosferă. În funcţie de posibilităţile familiilor, mulţi rezistă doar cu ajutorul orelor particulare; alţii au nevoie de psihiatru, iar totul se întâmplă în numele celor câţiva elevi beneficiari reali ai sistemului, care o vor lua clar pe o linie reală (studii ulterioare axate pe matematică). Ah, da, şi totul se întâmplă desigur şi în numele profesorului sau a şcolii, care este considerat/ă bun/ă.

Cât despre restul elevilor, al claselor sau chiar al şcolilor, toţi cei care nu intră în această goană după rezultate la olimpiade, sau nu-i fac faţă, sunt din start catalogaţi mai mult sau mai puţin slabi, rataţi, “ei nu sunt de succes” etc. Ce frustrare aduce acestă politică la nivelul întregii ţări? Nimeni nu discută oficial de acest aspect.

3) Singura direcţie ce se justifică cât de cât este învăţarea matematicii pentru examen, dar această motivaţie nu ţine la elevii claselor începătoare de ciclu (5-6, respectiv 9-10). Ca atare, deoarece la acest nivel profesorii nu ştiu altă tactică, matematica este introdusă şi abordată în stil clasic, adică prin metode specifice statului poliţienesc dictatorial autoritarist. De abia prin a 8-a, respectiv prin11-a elevii încep să înveţe cu adevărat pentru examen. Dar ce se întâmplă la clasele care nu au examen de matematică la BAC? Aceştia refuză cu totul matematică. Reacţia alergică este atât de brutală încât o mare parte a populaţiei şcolare nu apucă să beneficieze de factorul formator al matematicii, de acele aspecte prin care matematica le va folosii o viaţă întreagă: gândire logică, luarea unor decizii raţionale, capacitatea de a nu fi influenţabil etc. Fără să mai discutăm de utilitatea acestor cunoştinţe pentru cei care decid să mai rămână în sistem pentru încă un ciclu de învăţământ, de pildă într-o Politehnică. Exact acest al treilea aspect îl evocă Moise Guran în a doua idee a introducerii sale:

MG: Pe vremuri, pe vremuri mai golăneşti aşa, pe când eram eu în liceu iar Revoluţia ne făcuse să credem că democraţia înseamnă să stăm cu profii la fumat şi uneori şi prin baruri, un amic i-a pus aproximativ aceeaşi întrebare profesorului nostru de matematică: “Domnu’, dacă n-ar fi Bacalaureatul iar noi n-am fi la mate-fizică, ne-ar trebui la ceva matematica asta în viaţă?”, iar profesorul nostru de atunci, un gentelman de care îmi amintesc cu plăcere, deşi nu prea mă scotea din 5 şi 6, a zis cam aşa: “Da, tinere domn, ca să ştii şi tu câte pahare poţi să bei înainte să nu te mai poţi ridica de pe scaun”.

Desigur că întrebarea “La ce ne ajută matematica?” este una profund retorică. Până la momentul când elevul respectiv şi-a luat curajul să-şi întrebe profesorul/ profesoara, el s-a simţit din plin agresat de această materie, a auzit deja acasă sau în grupul de prieteni această întrebare, şi pentru el punerea întrebării este doar un act de sfidare a autorităţi în faţa celorlalţi. Ca urmare, orice răspuns just sau explicativ este în van. Doar un răspuns subtil înjositor poate să “salveze pielea”, adică onoarea dascălului în ochii colegilor: dacă răspunsul face faţă provocării, atunci cei din  “audienţă”vor ţine minte răspunsul (cum bine o dovedeşte Moise Guran): “ce l-a făcut pe ăla!”. În rest, puteţi să fiţi siguri: chiar pe nici un elev nu-l interesează la ce foloseşte matematica (şi asta nu din răutate; pur şi simplu, la vârstele şcolare nu este normal să te intereseze aşa ceva). CTG

Când stabileam la începutul lui octombrie că voi ţine pe 7 noiembrie o lecţie descisă cu colegii din cercul metodic despre predarea ariei cercului, nu mă gândeam că subiectul va ajunge înainte de sosirea iernii “pe buzele tuturor”. Iar când am scris de curând despre eleva care mi-a dat într-o lucrare fulger pentru numărul π valoarea 14,3 nu am putut bănui că tocmai deschid o nouă serie comică despre aria cercului. Pur şi simplu nu aveam de unde intui că un jurnalist se va trezi să întrebe pe un candidat la funcţia de preşedinte al ţării despre aria cercului. Nu consider formula de arie a cercului drept un etalon general de inteligenţă, dar în anumite cazuri speciale poate fi totuşi folositor ca un indicator în acest sens.

Redeschid aşadar tema despre acest număr magnific. Va fi probabil o succesiune destul de “colorată” de postări, în care voi trata atât evenimentele din această campanie electorală, cât şi aspectele metodice evidenţiate, inclusiv gândurile din spatele şi din timpul orei deschise din 7 noiembrie.

Deşi mi-am propus să ascult dezbaterea din seara zilei de 19 noiembrie pentru turul doi la alegerile prezidenţiale, cumva am ratat momentul de aur când şi-a făcut apariţia spectaculoasă în discuţie numărul π, prin omiterea sa de către D-na Dăncilă în propria-i conferinţă de presă. Am auzit în acea seară despre întâmplare, dar primele înregistrări auzite au fost cele de a doua zi, în drum spre şcoală. Acestea (fiind deja aranjate) sunau ceva de genul R pătrat, Pi R pătrat!, aducându-mi aminte de celebra replică din filmul cu James Bond, în care acesta se prezintă: Bond, James Bond. Dacă ar fi fost gândită intenţionat ca o glumă, atunci mai înţelegeam, dar aşa, replica contrafăcută de a doua zi dimineaţa, prin intenţia sa de a ascunde adevărul, doar îl certifică.

Repede însă ne-am dat seama de magnitudinea scandalului iscat cu o seară înainte. De fapt, nu răspunsul D-nei Dăncilă cu lipsa renumitului număr iraţional transcendent prezintă uriaşul dezastru în care ne aflăm, aşa cum s-a năpustit să considere mare parte a presei şi a societăţii. Nu, nu răspunsul D-nei Candidat la cea mai înaltă funcţie în stat reprezintă marea problemă, ci faptul că s-a ajuns în situaţia atât de josnică încât unui reporter să-i treacă prin minte să pună această întrebare, vădit intenţionat, pentru a scoate în evidenţă nivelul de cultură al acestui candidat. La fel cum în urmă cu cinci ani un reporter îl întreba pe Kandidatul din vremea respectivă dacă ştie imnul României, la fel acum s-a trezit careva s-o întrebe pe D-na Dăncilă despre aria cercului. Diferenţa este că, acu’ cinci ani Werner se pregătise pentru o astfel de situaţie şi fiind şi om umblat pe la corul bisericii, a făcut faţă cu brio provocării.

Dar să revenim la D-na Pi-orica şi la semnificaţia respectivei provocări. Această întrebare împreună cu răspunsul respectiv scot în evidenţă nivelul intelectual incredibil de scăzut la care a ajuns partidul care este responsabil în societatea românească pentru spectrul de stânga, pentru nivelul de preocupare social. Stânga românească a ajuns actualmente la un nivel de cultură inimaginabil de scăzut în trecut, chiar şi în urmă cu 10 ani. Sigur nu ne putem închipui o astfel de întrebare pusă pe vremuri, la candidatura D-lui Mircea Geoană, de pildă. Îmi este milă cu adevărat de toate persoanele culte ce împărtăşesc cinstit viziuni de stânga. Sunt făcuţi de râs în faţa celorlalţi, chiar şi în faţa lor sau a famililor. Sunt înjosiţi, deşi nu meritau asta. Nu asta înseamnă a fi de stânga; nu asta înseamnă social-democraţie. Dar destul cu politica. Haideţi să facem o scurtă trecere (cât de cât mai apropiată de matematică) asupra acestor evenimente din 19-20 noiembrie 2019 (doar aşa, ca să rămână undeva fixate, pentru amintire).
Odată cu întrebarea şi cu respectivul răspuns, “toată ţara” s-a năpustit pe internet să-şi refresh-uiască cunoştinele despre subiectul cu pricina, aria cercului devenind pentru scurt timp cea mai căutată sintagmă pe Google, cu peste 200.000 de căutări (Raluca Ion, Republica, Aria cercului, cea mai căutată sintagmă pe Google). Alţii inventau titluri şi mai “colorate”: Aria cercului – Cea mai căutată formulă pe Google după ce Dăncilă a dat-o de gard, cu un vârf de 100.000 de căutări în seara de 19 noiembrie (Aria cercului – Cea mai căutată formulă pe Google după ce Dăncilă a dat-o de gard)

Mult mai hotărât s-a arătat Dl. Cristian Tudor Popescu: PSD ar trebui să se numească de acum înainte πSD, pentru că π-ul necunoscut dnei Dăncilă va fi ţinut minte de toată lumea. (Pe vremuri, când organizam cu soţia ziua lui π, în pauză serveam elevii cu π-scuiţi (neapărat rotunzi) iar după pauză doritorii îşi puteau confecţiona o π-lărie, aşa că propunerea D-lui CTP îmi place de minune.) Continuă dânsul:

Dna Dăncilă a răspuns clar, de bunăvoie şi nesilită de nimeni, în văzul şi auzul ţării întregi: „Raza la pătrat”. Aici, jurnalista care a pus întrebarea a greşit: nu trebuia să-i dea pe loc răspunsul corect, trebuia doar să-i spună „Eroare, doamnă Dăncilă”. Sau, mai rafinat, putea să-i „dezvăluie”: „Răspunsul corect este 2r²”. Cu siguranţă, candidata s-ar fi repezit, cum s-a agăţat şi de πr² să zică, da, doi er pătrat, aşa am spus şi eu; după aceea putea fi făcută de rahat la pătrat. Deci, Dăncilă nu s-a corectat imediat, cum minte gros acum πSD, ci a fost corectată imediat.

Trecând şi la “dezbaterea paralelă”, Dl Popescu nu-l iartă nici pe Kaiserului Klaus, care, la reluarea întrebării de către un reporter, a zâmbit larg fără să emită vreun sunet. C-adicătelea, e sub demnitatea mea de profesor de fizică să răspund la o aşa simplă întrebare. Bine, domnule preşedinte, i-aş fi spus. Dacă asta e prea de tot elementar, atunci spuneţi-ne, vă rog, formula de calcul a ariei sferei. (πSD, elipsa lui Dăncilă și Kaiserul Klaus)

Da, şi dacă tot am ajuns şi la aria sferei, despre care Arhimede a arătat că este de patru ori cât aria cercului de acelaşi diametru, ajungem vrem-nu-vrem şi la explozia de bancuri din săptămâna ce a urmat. Unul dintre cele mai “culte” bancuri a fost cel care vorbea despre Somaţia lui Arhimede către D-na Dăncilă, cerându-i să ne spună câte laturi are un cerc.

Apoi a venit ziua alegerilor şi am fost chemaţi la vot să alegem între 2D (a şti sau a nu şti aria cercului; trebuia să spun oare 1D?) şi 3D (oare K ştia aria sferei?). Cel mai tare a fost ex-premierul Mihai Tudose, care a spus că: am votat şi pentru redarea prestigiului formulelor matematice. Adică, ce-a vrut să spună? Iar luni dimineaţă se zvonea că D-na Candidat πSD ar fi luat în diaspora 3,14%! (fapt care-i desigur fals, da’ bancu-i bun)

Încercând să închei trebuie să mai punctez doar meritul Andreei Dumitrescu (Realitatea Plus) care în finalul conferinţei de presă a pus întrebarea de pomină cu aria cercului. Cât despre D-na Dăncilă, a strâns peste 3,14 mil. de voturi? A strâns! Şi oricum, chiar dacă a πRdut, trebuie să-i mulţumim din suflet: niciodată matematica şcolară elementară nu a fost pe buzele tuturor ca acum (cu bucurie şi veselie pe buzele tuturor!). Toată lumea ştie mai nou aria cercului, toţi elevii ştiu acum formula cu pricina (chiar şi draga de ea, eleva cu 14,3). Nu se putea imagina o plecare mai spectaculoasă din politica de vârf, decât această ieşire pe acorduri matematice. CTG

Pe lungile autostrăzi din Germania ascultam diferite posturi de radio. Când nu mai recepţiona bine postul ascultat, radio-ul sărea automat la alt post. În toată această perioadă, din când în când auzeam o melodie ce mi-a atras atenţia în mod special. Era o melodie cu deosebite inflexiuni, cu o melodicitate absolut specială, cu un sound care părea retro, aducându-mi aminte de anii ’80, dar totuşi clar o melodie nouă, actuală.

De prima dată am avut impresia că o mai auzisem, dar nu ştiam “de unde să o iau”. Apoi, cred că la a patra audiţie, fiica mea a căutat-o cu aplicaţia de pe telefon şi am stabilit că melodia se numea So Am I şi era cântată de Ava Max. Aceasta este cântăreaţa aia cu Sweet but psicho.

Ne bucuram foarte mult când suna melodia din difuzoare; o auzeam cam o dată pe zi. Destul de repede mintea mea – atâta cât putea să fie de activă în paralel cu condusul la viteze medii de 140 km/h (pe tronsoanele fără reparaţii) – mintea mea “vedea” un soi de imagini interioare mişcătoare în acord cu inflexiunile acestei melodii. Mintea mea genera un film interior al acestei melodii, un film potrivit desigur doar minţii mele, percepţiilor mele. Sunt sigur că soţia mea şi fiica mea aveau cu totul alte senzaţii decât mine la această melodie.

Odată intorşi acasă nu am mai auzit melodia; prima dată am auzit-o din nou de abia după două săptămâni. Aşa că am căutat-o pe net să o văd. Şi, surpriză: videoclipul melodiei nu era nici pe departe potrivit percepţiilor şi imaginaţilor mele. În Germania în timpul condusului nu reuşisem să fiu atent şi la text (engleza mea nu curge atât de fluent ca şi germana; de multe ori când aud o melodie în mod repetat, doar la radio, mai întâi percep doar melodia, iar apoi la fiecare reaudiţie noi şi noi pasaje din text; asta şi datorită faptului că de obicei când asculţi muzică la radio, în paralel faci şi altceva). Acum, în faţa videoclipului, eram atent la text şi la mesajul melodiei, la căntăreaţă, la celelalte personaje şi la felul cum dansează, şi descopeream o cu totul nouă melodie, care nu se potrivea deloc cu filmul interior de pe lungile perioade de condus pe autostrăzile nemţeşti. Imaginile oficiale erau cu totul străine de trăirile mele, deşi era vorba de una şi aceaşi melodie. Între timp, în toamnă aceasta a ajuns să fie difuzată şi la noi, fiind destul de cunoscută şi intrind pe parcursul obişnuit de creştere, apoi de banalizare lentă.

Dacă nu cunoaşteţi melodia o puteţi asculta pe youtube (Ava Max – So am I, o melodie numai bună de ascultat în maşină, spune comentatorul de la Europa fm, azi sâmbătă 16 Noi. pe la ora 9.30, exact în momentul când m-am apucat să scriu această completare), dar dacă nu o cunoaşteţi, atunci nu rataţi ocazia şi faceţi experimentul descris mai sus, ascultând mai întâi de câteva ori melodia fără a vă uita la videoclip.

Dar oare, de ce vă povestesc dvs. toate acestea pe un blog despre predarea matematicii? Doar, n-am găsit matematică şi la Ava Max? Nu, staţi liniştiţi. Dar, deja din timpul acelor lungi perioade de condus mi-a încolţit în minte o idee, anume deosebita analogie între filmul interior generat de mintea mea la auzul acelei melodii şi felul în care mintea naturală şi vie a copilului generează şi vede modele comportamentale ale numerelor în procesul de învăţare a lecţiilor.

În acest moment al pledoariei sunt tentat să reiau pasaje dintr-o postare din vară, despre deschiderea matematicii (http://pentagonia.ro/opening-mathematics-deschiderea-matematicii/): Realitatea structurilor matematice poate fi vieţuită doar prin producerea interioară … învăţăceii ar trebui să poată începe cu a produce gânduri …

De ce a început mintea mea să vadă forme şi pete mişcându-se în fundal? Pentru că i s-a permis, pentru că a avut ocazia: mintea mea primea în acele momente doar melodia, nu şi videoclipul, şi acele pete se mişcau atât de frumos! Atunci când văd direct videoclipul unei melodii, mintea mea nu generează nici un film interior; mintea mea preia imediat filmul generat de regizor (merită să recitiţi articolul sus menţionat).

În tinereţe, pe vremea lui Ceauşescu, aveam melodiile doar înregistrate pe bandă audio (de obicei pe casete), deci nu le vedeam şi videoclipul. În acea perioadă aveam deseori senzaţia unui film interior la diferite melodii. De pildă, eu am reuşit să-mi înregistrez o copie după albumul Thriller al lui Michael Jackson înaintea Crăciunului din 1984. În acea vacanţă plină de zăpadă am ascultat masiv acest album. Ningea constant în fiecare noapte cam 50 cm, dar datorită greutăţii stratul total nu se mai ridica mult peste un metru. Pentru mine melodiile de pe acest album sunt fără discuţie melodii de iarnă şi indiferent de oricâte ori am vizionat clipurile respective, tot nu s-a putut şterge din mintea mea acea senzaţie de iarnă. Concret, în mintea mea există câte două “foldere” pentru  aceste melodii: când văd clipul, văd ce a vrut Michael Jackson să văd, dar când aud cântecul la radio simt automat atmosferă de iarnă.

Când s-ar putea ca mintea elevului să vadă modele comportamentale ale fenomenelor studiate? Desigur, atunci când nu v-a primi instant şi modele pre-fabricate de către alţii. Ce se întâmplă cu mintea unui elev care este obişnuită constant să primească modelul sau reţeta de rezolvare gată pregătită de către alţii? Simplu: nu va fi în stare să genereze un model propriu sau o rezolvare proprie de una’ singură.

Un elev a cărui minte a primit de-a lungul timpului doar rezolvări “de-a gata”, nu va putea nici o dată să rezolve o problemă de un tip nou, de care nu a mai văzut, pur şi simplu pentru că nu a fost antrenat să genereze idei noi. O predare a matematicii care constă doar din punerea de reţete în faţa elevilor, o astfel de predare nu va putea forma  minţi care să gândească.

În acelaşi fel, un elev neobişnuit să gândească, măcar în timpul unei rezolvări, acesta nu va putea să regândească o problemă căreia i-a uitat rezolvarea. Din păcate, există chiar şi la liceu profesori care le cer elevilor constant să înveţe rezolvări pe de rost. Ne putem imagina drama unui astfel de elev în clasa aVIII-a sau în a XII-a. El a fost obişnuit la fiecare capitol, cel mult pentru fiecare teză, din câteva capitole, să înveţe pe de rost toate rezolvările specifice, iar dacă s-a antrenat de mic în acest sens, reuşeşte constant lucrări de 10. Apoi vine perioada când este verificat din toată materia de patru ani. Dacă face teste recapitulative acasă, are posibilitatea să tot caute rezolvările uitate, dar atunci când este confruntat cu simulări la clasă (oficiale sau neoficiale), acest elev clachează şi este pur şi simplu îngenuncheat de incapacitatea sa de a gândi pe o situaţie pentru care nu-şi mai aduce aminte rezolvarea sau pe o situaţie pentru care nu s-a pregătit în acel format. Căderea este dură şi buimăcitoare (chiar până la nivelul de 6-7) şi nimic nu-l mai poate ajuta în acele momente. Un profesor care-i obişnuieşte pe elevi în acest fel, acesta cu greu poate fi denumit profesor de matematică.

Dacă aţi prins ideea, atunci vă las de aici să gândiţi dvs. de ce mă agit atât de mult să introduc cât mai des în lecţiile mele pasaje de predare prin problematizare, împingându-i pe elevi să descopere pe rând momentele lecţiei (sau ale rezolvării unei probleme) în urma unui proces “de cercetare” pe care îl putem numi şi predare prin întrebări (sau rezolvare prin întrebări). Desigur că acest tip de predare nu este posibil întotdeauna şi desigur că nu-mi reuşeşte la toţi elevii, dar cei care reuşesc măcar uneori să dea răspunsuri bune, aceştia sunt pe calea cea bună spre formarea unei minţi care chiar gândeşte, nu doar acumulează reţete de rezolvare. Titus auf der Autobahn

În emisiunea La radio din 28.09 2019 de la Europa fm, d-na Andreea Esca i-a avut ca invitaţi pe Măriuca şi Florin Talpeş, fondatorii firmei Bitdefender. Am ales din această emisiune câteva citate care ar trebui să ne dea de gândit, atât nouă celor de la bază, cât şi celor care se ocupă în mod organizatoric de învăţământul matematic românesc. Emisiunea merită ascultată cap-coadă de către orice profesor de matematică; eu am găsit-o la adresa https://www.europafm.ro/reasculta-emisiuni/ .

Din start aceştia precizează: Suntem formaţi de şcoala de matematică din România. Apoi îi auzim vorbind despre profesori cu har şi despre sprijinirea acestora, despre lipsa orelor aplicate (lucru de mână, traforaj etc.). Ceva mai târziu aflăm ce a zis Andrew Wiles la Roma:  problema nu e cu copiii, problema e cu profesorii: adică, nu că de fapt copiii nu iubesc matematica, problema e că sunt prea mulţi profesori de matematică care nu iubesc matematica. Asta o fi “la ei”, dar în nici un caz “la noi”; la noi sunt sigur că toţi profesorii iubesc matematica, problema este care matematică? (nu intru în acest subiect, l-am mai tratat cu alte ocazii; precizez doar pe scurt că – după părerea mea – în prea multe cazuri matematica spre care se preocupă profesorii nu este matematica potrivită elevilor). Dacă v-a scăpat, precizez că Andrew Wiles este cel care a reuşit să demonstreze Teorema lui Fermat în 1995 (vezi Simon Singh, Marea teoremă a lui Fermat, Ed. Humanitas)

Dl. Talpeş aprofundează tema, abordând frontal subiectul nivelului matematicii şcolare româneşti, nu a matematicii de excelenţă, ci a matematicii de masă. Astfel, dânsul aminteşte despre o discuţie cu Dl. Hanushek din SUA, economist la Universitatea Stanfort, discuţie avută la Summitul RBL (proiect de educatie): Ce impact ar avea o crestere a educatiei asupra PIB-ului in Romania?, iar răspunsul a fost următorul: daca generatia care se naşte astăzi va fi la 14 ani cu zero analfabeti functionali sau vom reuşi la examenul PISA să fim la nivelul Cehiei, adică să ridicăm cu 20 de puncte nivelul care îl avem azi la aceste examene, vom creşte PIB-ul Romaniei cu 1500.000.000.000 (1500 miliade) lei şi cu 15% an de an salariile din România. Deci, impactul în economie a unei educaţii mai bune este imens.. Şi l-am întrebat ce aţi face, spuneţi-ne trei lucruri ce le-aţi face: păi, simplu, m-aş ocupa de profesori, de profesori şi de profesori

Spre final mi-a atras atenţia următoarea afirmaţie: Studiile arată că cel mai mare progres profesorii îl fac învăţând unii de la alţii, nu cursuri, nu citind cărţi, ci învăţând unii de la alţii. Această afirmaţie este absolut şocantă în contextul în care de atâţia ani suntem obligaţi să participăm la cursuri de formare, cursuri de cele mai multe ori măcar parţial sterile, cursuri la care mai nimeni nu vrea să meargă, dar suntem obligaţi pentru că avem nevoie de “hârtia” respectivă şi de “punctele” aferente. Suntem oficial subjugaţi unui sistem în care unii câştigă de pe urma noastră, noi fiind obligaţi prin lege să le fim clienţi. Şi credeţi-mă, ştiu ce vorbesc: sunt unul dintre norocoşii care am avut ocazia să particip şi la cursuri în străinătate (sau cu profesori din străinătate) şi am avut şansa să văd şi să simt clar diferenţa. Pentru liniştea cititorului precizez că nu toate au fost lăudabile. Am în amintire şi două (*) la care îmi pare rău că m-am înscris, dar raportul acestora faţă de cele generatoare de amintiri profund pozitive este de cca. 1:10. La cursurile urmate cu formatori români raportul este orientativ invers! (* mă refer la câte un curs de 4-5 şedinţe de o oră jumate, parte a unui seminar de 5 zile cu cursuri de dimineaţa până seara)

Cât despre sfatul de a învăţa unii de la alţii în mod direct, trebuie să precizez că eu am asistat – cu titlul de a învăţa, nu cu titlul de a verifica – la ore la alţi profesori un total de cca. o lună (în Germania şi în România). Cât despre învăţatul din cărţi, aici părerea mea este că, după ce te-ai “pus pe linia corectă” preluând de la alţii, vei creşte mai departe doar dacă vei intra într-un proces de autodezvoltare prin proprie strădanie, iar asta nu se poate face decât prin intermediul cărţilor. Problema este desigur, ce cărţi alegi pentru a te forma (despre cărţile alese de mine şi de soţia mea am scris în nenumărate rânduri). Din fericire există foarte multe cărţi potrivite acestui scop, scrise sau traduse în limba română. Din păcate, majoritatea profesorilor habar nu au de aceste. Pentru cei mai mulţi profesori de matematică contează doar culegerile; cei mai mulţi nici nu conştientizează că există şi cărţi despre matematică sau despre predarea matematicii. CTG

P.S. Dacă tot vorbirăm de învăţat unii de la alţii, anunţ şi pe această cale că joi 7 noiembrie 2019 (ora 13)  voi ţine o lecţie deschisă (o oră cu elemente de tip “laborator de matematică”) cu tema Aria cercului şi numărul pi (ştiu că pedanţii spun aria discului, dar dacă dorim să venim în întâmpinarea marii mase a elevilor, trebuie să renunţăm pe cât posibil la aceste pedanterii obsesive: aşa cum vorbim despre aria triunghiului sau aria pătratului, putem liniştit vorbi şi despre aria cercului). Cine doreşte este binevenit la această activitate la Liceul Waldorf din Cluj.