Moise Guran a vorbit la Pastila Biziday de la Europa fm din 5 dec. 2019 sub titlul Cum se face că avem un preşedinte inspector şcolar şi un fost premier analfabet funcţional despre realitatea învăţământului şcolar românesc. Permiteţi-mi să vă vorbesc în acest comentariu despre manifestarea structurii de autoritate piramidală, de sorginte comunistă, a învăţământului şcolar românesc, atât de bine scoasă în evidenţă de către Dl. Guran.
El, inspectorul, are alte griji: el trebuie să aibă relaţii la partidul de guvernare, să-şi identifice şi să-şi găsească proptele în noul partid de guvernare, atunci când vin “ăialalţi”, să-şi alimenteze puterea din sursă sigură, ca să o poată împărăţi mai departe, mai micilor “Dumnezei” numiţi Directorii de şcoli. Aţi văzut vreo dată un director de şcoală ţipând la profesori? Dar un inspector ţipând la directori? Dar un primar sau un şef de Consiliu judeţean ţipând la inspectori, aţi văzut? Pentru că nu e nici o diferenţă între aceste manifestări de putere şi bullying-ul de zi cu zi pe care în final profesorul îl face asupra copiilor. (…)
Vă rog să mă scuzaţi, puterea exemplului funcţionează: (…) diploma este totuşi suficientă, dar numai dacă vrei să lucrezi la stat, să urci pe ierarhia asta de partid cu sau fără carnet, în care cu cât eşti mai obedient faţă de superiori şi ţipi mai tare la subordonaţi, vei ajunge tot mai sus, poate intr-o zi în vârful învăţământului românesc, al administraţiei, al poliţiei sau chiar al politicii româneşti.
*
Este pentru prima dată când aud vorbindu-se despre acest fenomen în mass-media românească, cel puţin la nivelul acesta de audienţă, dar şi de claritate. Nu, d-le Guran, nu am văzut cum un inspector să ţipe la directori, dar am simţit cum un inspector să agreseze relativ calm, dar sarcastic şi cu multe subînţelesuri o sală întreagă de directori (eram unul dintre ei). Din fericire, pot să spun că se pare că la Cluj au cam trecut acele vremuri. Comparând cu ce ştiu din alte judeţe, am convingerea că la Cluj inspectorii chiar sunt mult mai civilizaţi vizavi de directori (şi nu mai fac “din astea”).
Am văzut însă cum un inspector din minister ţipa la inspectorii responsabili cu alternativele educaţionale din toate judeţele (erau către 100 de inspectori). Stăteam la uşă, în exteriorul sălii respective cu 2-3 colegi şi ne cruceam; nu ne venea a crede! A fost groaznic, deşi nu noi eram cei vizaţi.
Cine vrea să aibă măcar o vagă idee despre cum a fost, să se mai uite la filmările făcute cu ocazia vizitei inopinate ale D-nei Ministru Anisie la şcolile din Ialomiţa: o acţiune de forţă şi înjosire a celor care sunt poziţionaţi mai jos pe scara ierarhică. Imaginaţi-vă ce putea să răspundă învăţătoarea respectivă la întrebările D-nei Ministru. Sau ce autoritate mai are dânsa în faţa elevilor (sigur nu mai are nivelul de autoritate corespunzător căruia striga doar uneori la elevi). Am vrea să fie altfel lucrurile înţara asta? Da! Dar nu aşa se schimbă lucrurile D-nă Ministru. În felul acesta doar reuşiţi să vă integraţi perfect în tabloul prezentat atât de bine de Moise Guran. În felul acesta arătaţi doar că faceţi parte din întregul sistem care este incapabil a se autoschimba, indiferent de partidul din care face parte unul sau celălalt.
Aici Moise Guran atinge poate cel mai bine susrsa acelui fenomen despre care tot ne vorbea Liviu Dragnea: România paralelă! Dânsul vorbea de România paralelă cu cea în care trăia dânsul. Da, există două Românii paralele, şi ca în bancul respectiv, fiecare îl ceartă pe celălalt că “de ce stă pe partea cealaltă a străzii?”. (Apropos: ştiaţi de ce traversează Adele strada? Ca să ne cânte “Hello from the other side!”) Cred că mă opresc aici, pentru că m-am îndepărtat oricum mult prea mult de predarea matematicii. CTG
P.S. Nici vorbă să fi terminat de discutat toate aspectele atinse de Moise Guran în cele cinci minute BiziDay din 5 dec.2019, dar vă spun cinstit: nu mai am energie de a vorbi despre toate aceste aspecte care macină învăţământul românesc. Eu vreau să vorbesc despre “arta de a preda matematica” şi din păcate subiectul a divagat mult prea mult. Chiar mai mult, îmi doresc să termin cu comentariile cu iz politic şi să mă întorc cu totul în articole despre ora de matematică şi atât (cât mă va ţine, nu ştiu, dar sper că nu va mai fi nevoie să intervin prea des).
Mă rezum în final doar la a vă prezenta pentru ultima dată citatele pe care nu am apucat să le analizez şi pe care le las în sarcina dvs. (vă rog să le acordaţi gânduri, dar nu de tipul “ce mai vrea şi ăsta?”; încercaţi să fiţi realişti, încercaţi să vă puneţi pe dvs. şi zona dvs. de comfort sub semnul întrebării; încercaţi să vă gândiţi dacă nu cumva au şi ceilalţi dreptate; încercaţi să nu mai aşteptaţi rezolvarea problemelor de la alţii, pentru că singurul pe care îl puteţi schimba este chiar persoana dvs.). Aşadar, vă doresc gânduri fructuase plecând de la următoarele idei: # Vanitatea unei caste cu o normă de 18 ore pe săptămână, # , responsabilă inconştient şi neacceptat de distrugerea a generaţii şi generaţii întregi de copii, care reprezintă de fapt viitorul ţării. # Ceea ce contează este doar capacitatea ta, a fiecăruia dintre noi, de a învăţa tot timpul, de a te adapta la nou. # Copiii noştri pleacă din şcoală fără să ştie măcar cum să înveţe singuri # fără a putea conştientiza că în societatea de azi succesul profesional nu este asociat cu afurisita aia de diplomă, ci cu foamea de permanent up-grade profesional. # Pentru că, vedeţi dumneavoastră, după ce importantul personaj – inspectorul – părăseşte lecţia deschisă, profesorul le poate dicta copiilor dintr-o carte (sau, cum am auzit de curând, de pe smart-board-ul pe care afişează cu sictir probleme gata rezolvate, putând astfel susţine şi că foloseşte mijloace moderne de învăţământ), # sau le poate preda plictisit şi mecanic o lecţie de la care cel mai des şi copiii şi profesorul absentează în realitate, chiar dacă sunt cu toţii acolo în clasă, înecaţi în formalism.
O singură întrebare am, d-le Moise Guran: cum aţi reuşit să găsiţi o legătură atât de rapidă între ideea de profesor dedicat şi – în mod automat – cei doi-trei copii dintr-o clasă, cu potenţial de olimpiadă? Adică, dacă te ocupi cu înverşunare şi de alţi elevi, alţii decât cei cu potenţial de olimpiadă, înseamnă că nu eşt profesor dedicat?
P.P.S. Permiteţi-mi să mă răzgândesc şi să vă mai reţin câteva minute, ca să vă vorbesc scurt despre un aspect neatins de Dl. Guran, neatins concret, dar la care i-a făcut cu mâna în trecere: cultul pentru necinste, pentru copiat, în general şcolirea pentru furat.
În finalul lucrării sale O scurtă istorie a românilor povestită celor tineri (Humanitas, 1999, pag. 210), regretatul Neagu Djuvara scria: Moştenirea cea mai tragică a regimului comunist constă în faptul că acea jumătate de secol ne-a stricat sufletul. Un regim în care minciuna a fost ridicată la rangul de metodă de guvernământ, în care teroarea a dezvoltat laşitatea la cei mai mulţi şi eroismul imprudent la cîţiva, în care delaţiunea a fost considerată virtute, în care furtul, nu numai din bunul statului dar şi din cel al vecinului, a sfârşit prin a apărea legitim din cauza privaţiunilor permanente şi a exemplului de înşelăciune venit de sus, un asemenea regim nu putea să nu lase urme profunde în mentalităţi şi comportamente. Ele sînt astăzi piedica majoră în integrarea noastră într-o lume nouă. Răul mi se pare atît de adînc şi de generalizat încît nu ştiu dacă generaţia celor care acum sînt tineri îl va mai putea stîrpi. Moralitatea batjocorită se repară mai greu decît uzinele învechite. Poate doar generaţiile următoare să reuşească a regăsi echilibrul, dacă ar şti, cu hotărîre, să impună cultul cinstei, al respectului pentru cuvîntul dat şi pentru semeni.
Să dau câteva exemple, pornind de la renumitul vers al lui Tudor Chirilă: am copiat la mate şi la sport. Sau, n-are rost, pentru că ştiţi şi dvs. destule exemple? Hai, totuşi să aruncăm o privire în jur, prin şcoli, încercăm totodată să evităm a vorbi despre forma tradiţională de furt în şcoli, adică despre copiat (copiatul temelor, pe vremuri în toalete, mai nou primite pe telefon, copiatul la lucrări, tema făcută de cineva acasă, copiatul la examene etc.).
1) Cum putem numi descărcarea deja tradiţională a referatelor de pe internet, altfel decât şcolire pentru furat, pardon, plagiat? Rămân blocat când câte un elev ameninţat cu corigenţa îmi sugerează cu tupeu “să-i dau un referat”. Ok, îţi dau un referat, dar cu o temă că nu-l găseşt pe net. Ah, nu aşa! Îmi răspunde, recunoscând astfel că spera să-i dau un referat despre Gauss, iar el să-l descarce. La o papetărie cu imprimantă (din Cluj) merg elevii de liceu cu sticul şi o roagă pe doamna respectivă să le scoată un referat pe hârtie rugând-o totodată să scrie şi numele lor acolo înainte de imprimare. Am un elev venit de la altă şcoală cu următoarea poveste (spusă de părinţi): învăţătoarea le-a cerut să facă un referat, iar elevul respectiv a lucrat două zile să-l compună, să-l scrie şi să lipească nişte poze, sub îndrumarea mamei. Când a venit la şcoală, învăţătoarea i l-a trântit şi l-a certat: nu ai putut şi tu să aduci un referat frumos descărcat de pe internet? Ce-I cu prostia asta?
2) Ce şcolire este aia în care la testul PISA un procent uriaş de elevi se dovedesc analfabeţi funcţional (la folosirea limbii materne sau a gândirii matematice), dar au promovat bine mersi clasele până la acea vârstă; păi, ori eşti de nota 2 sau 3, dar conform legii poţi promova clasa cu aceste note, ori promovezi clasele doar cu cel puţin 5, dar atunci chiar şti de 5, însemnând deci şi că nu eşti analfabet funcţional. Ei, la noi se poate şi să nu ştii şi să iei totuşi nota de trecere.
3) Cum am putea să descriem acele situaţii când un părinte vine la şcoală şi îl ia la rost de pidă pe profesorul de sport, pentru că îi strică media copilului său “eminent”, deşi acesta lipseşte regulat la orele de educaţie fizică, nu-şi dă normele şi este obraznic şi sfidător la adresa profesorului respectiv? Putem întreba şi invers: dacă pentru un 10 la matematică un elev trebuie să muncească foarte mult, de ce este plin de 10 sau de 9 la religie, pictură, muzică sau sport în cataloage? Această discuţie poate fi extinsă desigur în toate direcţiile, cum ar fi că părintele respectiv probabil că are impresia despre sine că este un om cinstit, sau – într-o direcţie relativ opusă – de ce un sistem care se consideră hipercorect prin faptul că face medie aritmetică între materii, de ce pune pe picior de egalitate media religiei (cu 1 oră săptămânală, dar şi cu noata 10 garantată) cu media matematicii (cu 4 ore pe săptămână, şi cu multă muncă necesară pentru o amărâtă de notă, să zicem 7). Ştiaţi că în sistemul examinărilor la şcolile de arte (muzică, arte plastice) notele 9 sau 8 reprezintă deja o înjosire eliminatorie?
4) De ce nu se fac în România orele până la ultima oră de vineri înainte de vacanţă, aşa ca în “ţările civilizate”? De ce profesorii le spun elevilor “vacanţă plăcută!” de marţi? De ce părinţii îşi duc copii cu o săptămână înainte de vacanţă la ţară? De ce copii chiulesc după ce s-au încheiat mediile? De ce în România părinţii îşi permit să plece în excursie cu familia în timpul şcolii? (fie şi în prima săptămână după vacanţă, cum s-a întâmplat acum la clasa a 8-a!).Ştiu de un elev a cărui familie a luat bilete în străinătate exact în perioada când copilul va avea teza (la o şcoală bună din Cluj). De toate am văzut sau am auzit: excursii cu familia în timpul şcolii în Ibiza, în Malta, la Roma, în Thailanda, în Finlanda, la Londra şi lista poate continua la nesfârşit (copilul întârzie puţin la şcoală: este în America cu tatăl său şi aşa am găsit bilete mai ieftine, iar întârziera a fost exact de două săptămâni – pentru că la început tot nu se face maru lucru!). Iar dacă profesorul se opune, aducem o scutire de o săptămână şi gata. Lăsaţi că recuperează, va zice părintele, încercând să muşamalizeze şi să nu vadă că tocmai i-a plantat puiuţului său în gândire un set de “norme de conduită şi etică” dăunător: Merge şi-aşa! sau Da’ ce-are? sau Profu’ are ceva cu copilul meu!. Da, avem grijă ca toate lucrurile cu care suntem obişnuiţi, inclusiv toate aceste lucruri urâte să le transmitem “cu sfinţenie” şi noilor generaţii, atât noi profesorii, cât şi dânşii părinţii.
5) Ca să înţelegem că dezastrul descris de Neagu Djuvara este generalizat, să luăm şi un exemplu, două, din vârful ierarhiei. Minciuna zilnică, adică lipsa totală a respectului pentru adevăr, duce la o stare generală de nepercepere profundă a “ADEVĂR”-ului. În România nu există “un adevăr”, ci există “adevărul meu” împotriva “adevărului tău” sau a “adevărului celuilalt”; la nivel înalt există chiar “adevărul meu de acum”, care peste o vreme se poate schimba radical în “adevărul meu de atunci”. De ce? Pentru că de la un anumit nivel în sus, şefii îşi permit această atitudine faţă de subalterni. Nu se înţelege ce spun?
Încercaţi să vă amintiţi care ministru al educaţiei încerca să desfiinţeze din răsputeri şcolile profesionale şi de ucenici pentru a umple liceele cu elevi care să devină apoi clienţii facultăţilor particulare? Într-o vreme se dorea chiar instituirea unei legi care să permită intratul la facultate fără BAC “sub promisiunea fermă că faci cumva să îl iei până la urmă” (aici societatea s-a sesizat până la urmă şi a oprit utopia). Cum putea respectiva persoană, reajunsă în funcţie peste ani, mai aproape de zilele noastre să ne vorbească liniştită despre “necesitatea reînfiinţării şcolilor profesionale”? Suntem proşti? Chiar nu avem ţinere de minte? (Apropos: nu am auzit comentarii în mass-media care să fi sesizat şi prezentat acest aspect)
O fi un singur exemplu de acest fel? Nici vorbă. Îl mai ţineţi minte pe Dl Preşedinte Băsescu cum ne asigura în 2009 că la noi nu vor scădea salariile, iar peste o vreme venea chiar el şi ne anunţa scăderea cu 25% a tuturor slariilor din sistemul bugetar? “Adevărul meu de acum”, total diferit “adevărul meu de atunci”. Ce educaţie poate face un sistem care vine în faţa “educabililor” cu astfel de modele? În aceste condiţii de ce să mă mir când un elev mă minte în faţă, având impresia că dacă el zice ceva, înseamnă că într-adevăr aşa şi este?
Acesta sunt cazuri legate de o persoană. Din păcate, aşa sunt făcute şi legile (la care eu nu mă pricep defel). La una am impulsul să zic “No, până aici!”. Ce părere aveţi de legea care permite înmatricularea în România de autoturisme cu volanul pe dreapta? Cum credeţi că v-aţi simţi când v-ar sării în faţă de după coloana din contrasens un BMW cu volanul pe partea greşită? Mă îngrozesc când îi văd. Cine a luat respectiva decizie de a permite astfel de înmatriculări? Sigur nu erau persoane cu o legătură sănătoasă cu adevărul şi cu judecata logică.
Sper că vă daţi seama că, dacă am sta mai mult la tema deschisă de Neagu Djuvara şi am face un pic de brain-storming, sigur s-ar mai găsi şi alte exemple Cred însă că mă opresc cu această listă urâtă aici, dar am convingerea că de la recunoaşterea acestor adevăruri şi a multor altora ar trebui pornită o reparare adevărată a situaţiei din şcoli (şi de aici mai departe în societatea românească, proces ce ar dura însă 20-30 de ani din momentul pornirii, cu condiţia desigur de a fi realizat just şi cinstit; cine ar avea forţa să-l facă just şi cinstit, asta este o altă discuţie).
P.P.P.S. Închei aici comentariile ideilor atinse (sau nu) de Moise Guran cu câteva gânduri chiar despre dânsul şi despre decizia sa din 15 ianuarie 2020 de a părăsi definitiv meseria de jurnalist şi de a trece în politică. Eu personal am resimţit puternic şi într-un mod relativ amar acest gest. Permiteţi-mi să mă justific.
O vorbă veche spune că “Dacă doi oameni îţi spun că eşti beat, mai bine du-te şi te culcă!”. Dar dacă aceasta se întâmplă într-o dispută în care totuşi simţi cu adevărat ai dreptate, ce faci? Abandonezi lupta şi laşi după ceilalţi, pentru că sunt mai mulţi? Sau te înverşunezi şi totuşi lupţi, te angajezi la o luptă de durată, conştient fiind că cei de altă părere sunt mulţi iar lupta va fi cu atât mai grea. În aceste condiţii însă, trebuie să fi foarte puternic pe poziţie, mai ales atunci când ai un crez profund (un crez pentru care ai şi dovezi clare), un crez care este însă contrazis de marea majoritate a celor din jur.
Acesta este şi cazul meu: de ani buni (peste 25 ani) duc o “luptă” ciudată pentru o predare mai umană a matematicii. În această “luptă”, fiind în opoziţia constantă faţă de marea parte a sistemului, mă ajută desigur fiecare dovadă că şi altcineva gândeşte la fel, că şi altcineva a văzut aceleaşi aspecte, chiar dacă majoritatea celor din jur parcă preferă “să se uite în altă parte”. În acest context m-am bucurat de fiecare dată când am auzit vreun jurnalist exprimându-se coerent, realist şi analist despre predarea matematicii. Moise Guran a fost unul dintre cei mai activi în acest sens, iar activitatea sa prin comentariile şi analizele despre matematică, dar şi despre predare şi şcoală în general, îmi vor lipsi cu siguranţă. Mulţumesc “fostului jurnalist” Moise Guran – în numele tuturor care i-au apreciat comentariile – pentru tot sprijinul acordat de fiecare dată în înţelegerea situaţiilor cu care ne-am confruntat în învăţământul românesc, situaţii pe care din păcate autorităţile se feresc de obicei a le vedea şi a le rezolva.. Îi mulţumesc lui Moise Guran că mi-a arătat că nu eu sunt cel “beat”, ci ceilalţi.
Interesant este că eu îmi propusesem, aproape stabilisem că voi termina cu comentariile “politico-educative” chiar în weekend-ul dinaintea anunţului d-lui Guran (articolul de faţă a fost redactat la începutul lunii ianuarie). Foarte interesant! CTG

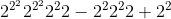 . Oare primarul lor este prof de mate? Nu de alta, dar au fost mai multe imagini cu mesaje matematice în setul de poze primit. Ti ∙ 101
. Oare primarul lor este prof de mate? Nu de alta, dar au fost mai multe imagini cu mesaje matematice în setul de poze primit. Ti ∙ 101
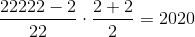 . Mie personal, cel mai mult mi-a plăcut următorul calcul: (9 ∙ 8 ∙ 7 + 6 – 5) ∙ 4 – 3 + 2 + 1 = 2020, deşi nici cu următorul nu te poţi plânge: 1 – 2 + (3!)4 + 5 + 6! = 2020. Pe de altă parte, cei pasionaţi de teorema lui Pitagora au amplificat tripleta egipteană 32 + 42 = 52 cu 404 şi au obţinut 12122 + 16162 = 20202.
. Mie personal, cel mai mult mi-a plăcut următorul calcul: (9 ∙ 8 ∙ 7 + 6 – 5) ∙ 4 – 3 + 2 + 1 = 2020, deşi nici cu următorul nu te poţi plânge: 1 – 2 + (3!)4 + 5 + 6! = 2020. Pe de altă parte, cei pasionaţi de teorema lui Pitagora au amplificat tripleta egipteană 32 + 42 = 52 cu 404 şi au obţinut 12122 + 16162 = 20202.