Moise Guran – pe când era încă jurnalist – a vorbit la Pastila Biziday de la Europa fm din 5 dec. 2019 sub titlul Cum se face că avem un preşedinte inspector şcolar şi un fost premier analfabet funcţional despre realitatea învăţământului şcolar românesc. Să analizăm în continuare pasajele legate de inspecţia la clasă.
Doamna Monica Anisie, actualul ministru al educaţiei este şi ea un fost inspector şcolar, la fel ca şi Preşedintele Klaus Iohannis. Trebuie că şi D-na Anisie şi Dl Iohannis au asistat de nenumărate ori la numerele de dresaj cu copii numite “lecţie deschisă”, “inspecţie la clasă”, “examen de grad”. Aceasta este metoda de evaluare a calităţii profesorilor în România: o şcenetă anunţată, repetată înainte, în care copiii ştiu ce întrebări va pune doamna la clasă, doamna ştie ce copii trebuie să răspundă şi la ce întrebări fiecare, iar un inspector plictisit ştie că asistă de fapt la un “montaj literar artistic”. (…)
Fără a generaliza şi fără a arunca anatema asupra (…) tuturor profesorilor, adevărul este că nu ştim în acest moment câţi dintre cei rămaşi în sistemul de educaţie mai sunt altfel, mai predau adică la clasă şi demnitatea umană. Pentru că, vedeţi dumneavoastră, după ce importantul personaj – inspectorul – părăseşte lecţia deschisă, profesorul le poate dicta copiilor dintr-o carte, aşa cum au mărturisit foştii elevi ai Vioricăi Dăncilă, de exemplu că făcea aceasta, le poate vorbi urât, poate urla la ei, le poate arăta semne obscene, şi credeţi-mă că nu vorbesc din teorie, sau – mai des – le poate preda plictisit şi mecanic o lecţie de la care cel mai des şi copiii şi profesorul absentează în realitate, chiar dacă sunt cu toţii acolo în clasă, înecaţi în formalism.
*
Eu consider că cel mai important punct al acestui citat îl reprezintă demnitatea umană. Cel care nu are în el demnitatea umană, acela şi-a ratat cariera, acela nici măcar nu ar avea voie să intre într-o clasă! Şi spun atât de hotărât acest gând datorită unui fapt puţin cunoscut şi deloc luat în seamă despre învăţământ: imitaţia!
Imitaţia este singura cale prin care copiii învaţă şi se formează până la vârsta de 7 ani. Orice aparentă învăţare raţională, pe bază de explicaţii, înainte de această vârstă este o falsă învăţare şi o dăunătoare intelectualizare mult prea timpurie. Doar după împlinirea vârstei de 7 ani încep să se deschidă în mod realist canalele de învăţare explicativă şi dobândire conştientă şi activă de cunoştinţe pentru creierul uman. Totuşi, acumularea de comportament, atitudine şi “felul de a fi” are loc în continuare şi după vârsta de 7 ani, predominant tot prin imitaţie, iar prezenţa în faţa clasei a unui personaj precum Viorica Dăncilă, par examplu, produce pagube greu de imaginat în marea masă a populaţiei şcolare cu care aceasta a interacţionat. Dacă dorim educarea demnităţii umane la întreaga populaţie şcolară, atunci trebuie să avem grijă ca în faţa claselor să ajungă doar persoane cu o solidă demnitate umană. Cum s-ar putea face chestia asta, asta este un alt subiect.
Dar să revenim la inspecţia la clasă. Îmi permit să vorbesc atât de degajat şi fără jenă despre acest subiect pentru că eu m-am înscris de mai multe ori la ţinerea unei lecţii deschise cu colegii din cercul metodic, şi pot povesti câte ceva suplimentar faţă de modelul tipic prezentat de Moise Guran (în plus, am mai ţinut şi o lecţie deschisă pentru care am fost desemnat să o ţin). Cele mai multe au ieşit bine sau foarte bine, dar despre ultima nu mă pot lăuda (sper să reuşesc în curând o analiză a acestei ultime ore, pentru că atinge câteva subiecte foarte actuale în finalul lui 2019).
Pe lângă acestea au fost şi inspecţiile pentru examenele de grad. Desigur că îţi pregăteşti aceste lecţii în mod deosebit. De ce? Pentru că de aia sunt făcute, ca să vadă musafirii ceva deosebit! Ţine de felul nostru de a fi; de a fi o “gazdă bună”.
Aşa suntem noi: dacă mergi în străinătate pe la rude şi prieteni (plecaţi din România), te vor ospeţi din plin. Dacă vei merge la prieteni străini, atunci cel mult te vor informa că poţi să te serveşti din frigider cu ce este şi îţi vor spune eventual unde este cel mai apropiat magazin. Ce-i drept, vor organiza şi o masă deosebită sau te vor scoate la restaurant, dar totul departe de strădania deosebită a “românului” de a te îndopa până îţi va veni “să explodezi” de atâta mâncare. Dar să revenim la orele cu “musafiri” la clasă.
Desigur că lecţiile deschise sunt deosebite de restul orelor şi asta se întâmplă din multe cauze. Nici măcar nu-mi pot permite într-un astfel de eseu să fac o analiză exhaustivă, atât de multe cauze există. Voi evidenţia doar două: una care ţine de cel inspectat şi una care ţine de cel aflat în vizită, ambele coexistând într-un fel de simbioză de nimeni analizată în mod realist. Pe de o parte este “gazda”, cadrul didactic care ţine ora respectivă şi care are desigur îndoieli asupra sa: oare, în realitate, corespunde el cerinţelor? Oare câte lipsuri are el, câte deficienţe prezintă activitatea sa de zi cu zi? Şi întrebările la adresa propriei persoane pot continua cu diferite nuanţe “mult şi bine”, dar acestea sunt ţinute ascunse în cotloanele personale cele mai adânci. Oare câte din acestea vor fi vizibile la lecţia deschisă, punându-te într-o poziţie vulnerabilă? Pe de cealaltă parte este “musafirul”, care însă nu se comportă neapărat ca un veritabil musafir, ci se crede de multe ori îndreptăţit în a critica, prin poziţia sa; starea societăţii noastre a ajuns chiar în faza în care aceşti musafiri se cred uneori chiar datori de a te critica, a-ţi găsi mici chiciţe de care să se lege, în cazul lipsei unor aspecte evident greşite.
Cine are impulsul de a spune că aceasta este o atitudine normală, acestuia îi precizez că nici vorbă; am avut mai multe ocazii să particip (ca director în Şcoala Waldorf) la ore ale colegilor alături de musafiri din Germania, veniţi să verifice calitatea şi nivelul waldorfului din şcoala noastră, şi trebuie să precizez că atitudinea acestora este una profund diferită de ceea ce suntem noi obişnuiţi.
Aruncând o privire sumară chiar şi numai asupra acestor două aspecte, şi înţelegem imediat cât este de dificil momentul unei lecţii deschise şi de ce oamenii se străduiesc să le facă deosebite. Asta nu-i scuză însă pe cei care prezintă “ore false”. Una este să prezinţi o oră cât mai bine pregătită, chiar regizată în mintea ta până în cel mai mic detaliu, şi alta este ca toată această pregătire să fi fost repetată şi exersată dinainte cu elevii. Nici nu vreau să discut de astfel de cazuri. Simt că m-ar îngreţoşa până la extrem.
Prefer dimpotrivă să vă povestesc două întâmplări din experienţa mea cu cu inspecţiile avute la clasă. Alte întâmplări de la ore deschise sau de inspecţie le voi povestii în articole viitoare separate, împreună cu conţinutul care a fost în aceste cazuri deosebit faţă de lecţiile cunoscute de toată lumea. Până atunci însă aş dori să vă povestesc cum mi-am permis eu “să fentez” sistemul într-un mod cât se poate de cinstit, ajungând chiar să-i povestesc după oră inspectorului despre ce am făcut.
Prima lecţie evocată a avut loc în primăvara lui1998, cu ocazia inspecţiei pentru gradul II (la vremea respectivă încă nu se făceau tot felul de preinspecţii). Aveam două clase în Şcoala Waldorf şi două clase în şcoala tradiţională unde eram titular. Ca inspector urma să vină o Doamnă Profesoară (profesoară cu P foarte mare!) total deosebită: în primul rând pentru că fusese colegă cu părinţii mei în facultate, astfel încât cădea din start posibilitatea unei atitudini prea severe la inspecţie; pe de altă parte aveam un respect apropiat de frică faţă de dânsa, pentru că era unul din autorii manualelor de geometrie pentru clasele 9-10 după care învăţasem în liceu (pentru mine era un fel de semizeu). Dar aveam şi eu ambiţiile mele: vroiam să folosesc ocazia pentru a-i dovedi unei mari personalităţi de ce sunt eu în stare, dar mai ales de faptul că Şcoala Waldorf nu este o şcoală pentru copii cu probleme la învăţătură, aşa cum susţineau cei mai mulţi.
Ne înţelesesem să fac două ore de aritmetică şi algebră la casele de la şcoala tradiţională şi două ore de geometrie care erau legate la clasa a VI-a din Waldorf (la vremea respectivă patrulaterele erau în clasa a VI-a, după triunghiuri). Atenţia cea mai mare a mea era asupra orei duble de geometrie, unde oricum mă simţeam cel mai în largul meu. Pentru a o impresiona pe Doamna Profesoară îmi pusesem două obiective clare pentru această oră: să fac o problemă “de olimpiadă” şi o problemă pe care dânsa să nu o ştie. În plus, totul trebuia să se lege impecabil, iar clasa trebuia să funcţioneze cum trebuie prin elevii buni pe care mă puteam baza. Dar nici prin cap nu-mi putea trece să fac o şcenetă anunţată şi înainte repetată, aşa cum vorbeşte Moise Guran.
Puteam însă să fac cu o zi înainte o lecţie de factură similară, astfel încât elevii să fie cumva setaţi pe lungimea de undă dorită. Practic, am regizat două ore duble în cascadă, în două zile consecutive. Prima oră din cele două din ziua precedentă aducea linia mijlocie în triunghi, iar a doua venea cu probleme în care linia mijlocie în triunghi se aplica în situaţii combinate împreună cu mediana pe ipotenuză şi altele. Apoi, în prima din cele două ore de la inspecţie urma să studiem linia mijlocie în trapez, iar apoi probleme combinate împreună cu linia mijlocie în triunghi, mediana pe ipotenuză, cateta opusă unghiului de 30o etc.
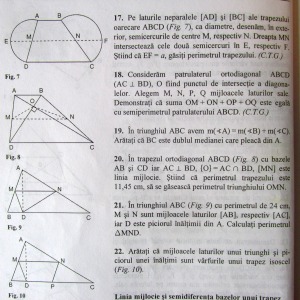
Pentru inspecţie găsisem o problemă cu linia mijlocie în trapez şi mediana pe ipotenuză, ce fusese dată la olimpiadă în acel an, şi care se potrivea perfect cu întregul demers. Mai îmi trebuia o problemă pe care Doamna Profesoară să nu o cunoască, pentru a o impresiona profund, dar pe care elevii mei să o ştie face, chiar dacă desigur nu-mi permiteam să le-o arăt dinainte. Concluzia era clară: aveam nevoie de două probleme similare, una cu linia mijlocie în triunghi şi una cu linia mijlocie în trapez, amândouă inventate de mine, plecând de la premiza că dânsa (ca autor de manuale de geometrie) ştia cam orice problemă deja existentă la nivelul la care eram eu cu elevii. Trebuia deci să compun două probleme total noi pentru aceste lecţii, astfel încât să parcurg problema cu linia mijlocie în triunghi în lecţia precedentă, iar elevii să ştie rezolva sigur problema cu linia mijlocie în trapez la inspecţia de grad. Măcar unul din clasă trebuia să poată face transferul.
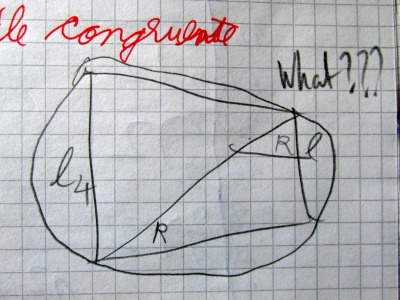
După 3-4 zile de gânduri şi strădanii mi-a venit ideea unor probleme cu două semicercuri construite pe laturile oblice ale unui triunghi oarecare, respectiv ale unui trapez oarecare. Prima trebuia să o facem la lecţia precedentă inspecţiei, astfel încât elevii să cunoască rezolvarea în principiu la cea de a doua problemă, la lecţia cu linia mijlocie în trapez de la inspecţie. În plus, cele două probleme precedau foarte fluent şi problema aleasă de la olimpiadă.
Puteţi vedea probleme din cele două lecţii succesive în următoarea imagine (din culegerea scrisă peste ani). Problema 17. este problema nouă în trepez (cea în triunghi este similară). Problema 20. este problema ce fusese dată de curând la olimpiadă (nu mai ţin minte ce fază (locală sau judeţeană). Problemele 21. şi 22. au participat şi ele la ispravă, dar nu mai ştiu în rest care probleme au mai fost implicate.
Cum a funcţionat toată treaba la inspecţie? Perfect! Sau, ar trebui să spun “mai mult ca perfect”! Doamna Profesoară, care era afundată într-o discuţie cu directoarea noastră, a sărit în picioare când a văzut figura pe tablă (nu fusese atentă la prezentarea problemei) şi a preluat pur şi simplu lecţia: “Ce se dă? Spune tu. Ce se cere? Spune tu. Cum se rezolvă? Poftim tu la tablă.”, hotărându-se asupra unei eleve care a ridicat mâna şi a început să explice cum s-ar rezolva. Apoi s-a întors în ultima bancă şi m-a lăsat să continui. După oră, întorşi în cabinetul unde urma să aibă loc o primă analiză, s-a uitat la mine zâmbind: “Ce mi-ai făcut, copile! De unde ai scos problema aia?” Am zâmbit cu gura până la urechi şi i-am povestit toată tărăşenia, cum îmi propusesem să o impresionez şi care a fost planul meu. Oricum, lecţia decursese foarte bine, fără ca elevii să cunoască conţinutul dinainte.
Următoarea întâmplare ce doresc să o evoc, tot într-o parţială contrazicere a celor prezentate de Moise Guran, este o experienţă ciudată, la trei ani după prima întâmplare. Eram înscris la gradul I când s-au introdus preinspecţiile, aşa că m-am trezit şi eu că urma să fiu pre-inspectat (ce-i drept numai o oră). Fusesem anunţat când şi la ce oră urma să vină profesorul desemnat în acest sens. Se potrivea la clasa a VII-a, aşa că am hotărât să fac o oră nou inventată de mine (conţinând teorema directă a liniei mijlocii în triunghi, ambele reciproce parţiale, cât şi reciproca totală; sper să vă pot prezenta în curând şi această lecţie deosebită pe pentagonia.ro). Tocmai compusesem lecţia respectivă, eram total entuziasmat despre aceasta şi urma să o prezint la acea inspecţie în premieră absolută în ziua cu pricina. Aşa că că m-am hotărât spontan în acea zi să fac o repetiţie generală a lecţiei respective la clasa a VIII-a, cu care aveam ora dinaintea inspecţiei (fiind o lecţia nouă, această clasă nu o văzuse cu un an înainte).
Pe vremea respectivă eram o şcoală mică, cu personalul la minim, directoarea făcea şi ore, doar femeia de servici umbla prin şcoală în timpul orelor. Aşa că am instruit-o că va veni un Domn Profesor pentru inspecţie la ora 11 şi că dacă apare mai devreme să-l poftească în mica săliţă ce o foloseam atât ca secretariat cât şi ca direcţiune.
Acum eram la clasa a VIII-a cărora le spusesem că le prezint sub titlu de probleme recapitulative la demonstraţii de geometrie plană o nouă lecţie de a mea, lecţie ce o voi face apoi şi ora următoare cu cei de a VII-a. Tocmai trecuseră cam 20 min. din ora la clasa a VIII-a, eram cam pe la jumătatea lecţiei, când uşa clasei se deschise şi femeia de servici îl împise pe Domnul Profesor în clasă. Nu-l mai văzusem nici o dată şi am rămas mască, iar singurul mod în care am putut să reacţionez a fost să-l salut şi să fiu 100% cinstit şi să-i explic ce se întâmplă. A spus că nu-i nimic, a luat loc într-o bancă şi a urmărit finalul lecţiei (eu nu puteam să fac altceva, nu puteam schimba subiectul, aş fi arătat necinstit şi ipocrit faţă de respectiva clasă a VIII-a, lecţia era pe jumate pe tablă şi dânsul oricum s-ar fi prins de întâmplare). Apoi, ora următoare a văzut lecţia de la cap la coadă la clasa a VII-a. Lecţia i-a plăcut, pre-inspecţia a ieşit bine, iar peste ani mi-a fost povestit de către cineva cât de frumos vorbea Domnul Profesor respectiv despre cele văzute cu acea ocazie.
Acestea au fost cele două exemple în care eu mi-am pregătit lecţia de la inspecţie mai mult decât ar fi obişnuit (mai neortodox, am putea spune). Am totuşi convingerea că am jucat cinstit, iar situaţiile respective nu pot fi încadrate la categoria o şcenetă anunţată, repetată înainte, în care copiii ştiu ce întrebări va pune doamna la clasă, doamna ştie ce copii trebuie să răspundă şi la ce întrebări fiecare, iar un inspector plictisit ştie că asistă de fapt la un “montaj literar artistic”. În schimb, chiar dacă eram hiperstresat la vremea respectivă (în mod diferit desigur în cele două situaţii), elevii mei au putut să vieţuiască totodată cu aceste ocazii şi demnitatea umană. CTG







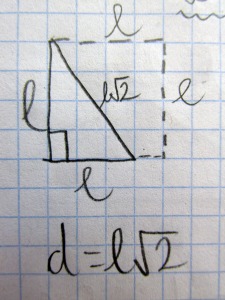
Observații la începutul anului 3 (după noua programă)
Mulțimi, segmente, unghiuri, divizibilitate și ecuații -clasa a VI-a.
Am stat mai bine de o lună la mulțimi, având o clasă medie, care nu a făcut nici o conexiune cu noțiunile predate în clasa a V-a.
La segmente și unghiuri am luat-o de la început ( sunt mulțimi de puncte, cu notații și tot meniul asociat, nu-i așa?), fără posibilitatea de a rezolva civilizat multitudinea de ecuații aferente.
Metodele aritmetice erau foarte bine predate de către învățători, acceptate și însușite de către elevi (fără exagerări, sume Gauss sau metoda ”algebrică”). Acum elevii intră în gimnaziu cu un bagaj matematic … extrem de modest, dar cu EN II și cu EN IV trecute cu succes!
Teorema lui Pitagora a devenit șarpele acestei programe.
Materia clasei a VII-a este extrem de lejeră, avem timp până și pentru jocuri didactice, În clasele V-VI nici vorbă de așa ceva (goana după olimpici).
Greul a rămas … pentru clasa a VIII-a.
Despre evaluare și mai ales despre Evaluarea națională din 2021 nu vorbește nimeni. Curriculum fără evaluare … nu există.
Poate nu am înțeles eu prea bine noua programă, dar am pierdut o groază de timp ! … A, peste trei săptămâni dăm teza. Atât.
Bravo, cu felicitări!