Prezentul eseu este gândit ca o scrisoare deschisă adresată d-lui Radu Gologan, preşedinte SSMR, şeful Comisiei pentru elaborarea noilor programe de matematică pentru clasele gimnaziale, cât şi tuturor membrilor comisiei. Propunerea oferită spre dezbatere publică la sfârşitul lunii ianuarie 2017 reprezintă cea mai plăcută surpriză posibilă, deschizând căi de vindecare şi evoluţie pozitivă a predării matematicii, căi de neimaginat până în urmă cu puţină vreme.
Această primă parte a eseului (de publicat înaintea termenului de 12 feb.) va fi direcţionată asupra conţinuturilor şi ordinii acestora, dar va conţine în argumentări şi elemente de metodică. În cea de a doua parte (ce urmează cât de repede posibil) voi analiza mai în amănunt metodica propusă. Din această a doua parte evidenţiez acum doar un singur aspect: întoarcerea în predarea matematicii a cuvântului intuiţie. În prezentul proiect, doar la nota de prezentare şi în sugestiile metodologice, acesta apare în diverse forme de 20 de ori (!!!), subliniindu-se astfel importanţa folosirii şi dezvoltării intuiţiei elevilor. Aşadar:
Stimate D-le Radu Gologan, stimaţi colegi,
Ca profesor activ în direcţia reformării predării matematicii de peste 20 de ani, vă felicit pentru acest proiect. În încercarea de a fi cât mai obiectiv (un ideal greu de atins) am structurat prezenta analiză pe patru categorii de păreri, numite cât de sugestiv posibil: 1) Da, cu aplauze; 2) Da, cu amendament; 3) Nu, cu alternativă; 4) Nu, cu avertisment. Din punct de vedere personal, proiectul este unul foarte reuşit, dovadă că primele trei categorii sunt încărcate, pe când ultima categorie este foarte “subţire”. Toate părerile şi comentariile expuse se bazează pe experienţa personală; pe majoritatea covârşitoare le cunosc foarte bine din aplicarea în activitatea personală (a mea şi a soţiei) din şcolile unde am predat. La toate aceste comentarii se poate face precizarea că opinia prezentată este în favoarea elevului, că aşa este cel mai sănătos pentru parcursul matematic al elevului. Înţeleg prin sănătos orice argument de ordin psihologic, legat de posibilităţile şi nevoile fiecărei vârste, dar şi a fiecărei categorii de elevi în parte. Acolo unde nu am o părere bazată pe experienţă directă, ci doar pe intuiţia dată de experienţa de ansamblu, acolo voi preciza acest aspect.
- DA, cu aplauze! Da, sunt cu totul de acord cu următoarele elemente:
- Da! conectării cmmdc şi cmmmc de simplificarea fracţiilor ordinare, respectiv de aducerea fracţiilor la numitor comun; aşa înţelege orice elev la ce sunt bune acestea, le găseşte imediat un sens. Da şi introducerii acestora prin enumerare şi intuitiv, nu prin algoritm. Aşa este sănătos!
- Da! aducerii înmulţirii şi împărţirii fracţiilor ordinare înapoi în clasa a V-a, imediat după adunare şi scădere. Da şi limitării pentru început la exerciţii mai uşoare.
- Da, poveştii cu tabla de şah (pag.7).
- Da! mutării noţiunii de mulţime din clasa a V-a la începutul clasei a VI-a. Atunci deja există o zestre de cunoştinţe matematice fixate ce pot fi folosite în exerciţii cu mulţimi. Astfel, în clasa a V-a aducem aspecte matematice noi, dar în sistemul de scriere cunoscut.
- Da, capitolului despre mulţimi şi structurare a cunoştinţelor despre numere naturale deja dobândite de la începutul clasei a VI-a. Simţeam că în clasa a V-a mulţimile, prin scrierea lor nouă, abstractă, îngreunează mult acomodarea elevilor la matematica de gimnaziu, dar nu aveam un gând clar unde ar trebui puse. Experienţa generală îmi spune că la începutul clasei a VI-a este foarte bine (dar nu le-am predat nici o dată astfel).
- Da! (cu ropote de aplauze şi urale!) scoaterii m-ului de la măsura unui unghi (pag. 9); undeva prin clasele VI-VII poate fi introdusă treptat, deşi în multe raţionamente acest m cu parantezele sale încarcă doar scrierea, devenind astfel pentru mulţi elevi o piedică, o îngreunare în înţelegerea raţionamentului expus.
- Da introducerii ecuaţiilor de-abia în clasa a VI-a, după învăţarea semnului unui număr. Atât unii profesori, cât şi părinţii, nu se puteau abţine să nu le zică elevilor încă din clasa a V-a că îl mutăm în membrul celălalt cu semn schimbat.
- DAAA! (cu cea mai mare bucurie) parcurgerii paralelelor tăiate de o secantă, respectiv a unghiurilor alterne interne, înaintea lecţiei despre triunghiuri. Astfel se poate studia – cu demonstraţie cu tot! – suma unghiurilor în triunghi din prima lecţie. Suma unghiurilor în triunghi este o aplicaţie cu pronunţat caracter aritmetic, accesibilă tuturor elevilor, care ajută în plus şi la stabilizarea înţelegerii noţiunii de unghi. Se încheie astfel o lungă perioadă aflată sub dominaţia predării riguros- axiomatice care impunea o ordine a lecţiilor ce sfida principiile natural-pedagogice (demonstraţia prin reducere la absurd, ce folosea congruenţa triunghiurilor, cu acel triunghi prelungit la infinit, nu se mai face de la Revoluţie; ca urmare nu mai este necesară de mult ordinea triunghiul → congruenţa triunghiurilor → unghiuri alterne interne → suma unghiurilor în triunghi). Eu personal predau în ordinea propusă de prezentul proiect din anul şcolar 1994-1995.
- Da! (cu lungi ovaţii!) reintroducerii cercului în “clubul noţiunilor fundamentale”, în primul capitol de geometrie din clasa a VI-a. Cred totuşi că poziţiile relative a două cercuri pot fi lăsate pentru clasa a VII-a (neesenţial).
- Da! (cu mare bucurie!) reintroducerii accentului pe construcţii geometrice cu diferitele instrumente, atât în clasa a V-a, cât mai ales în clasa a VI-a (inclusiv construcţia intuitivă a paralelelor prin translaţie, care este de mare valoare în formarea gândirii, dar care poate sta şi la baza explicării congruenţei unghiurilor corespondente). Cunoaşterea figurilor geometrice prin construirea acestora în diferite cazuri particulare este o cale deosebit de sănătoasă de învăţare. Acesta ar trebui aleasă ca tema definitorie (!) pentru clasa a VI-a. Apoi, în clasa a VII-a, când accentul se mută pe raţionament, pe demonstraţie şi calcule complicate, elevii pot folosi la nevoie doar schiţe, pentru că ei au deja fixată în minte figura corectă construită cu mare atenţie în clasa a VI-a.
- Da, (în conexiune directă cu precedentul) lecţiei Cazurile de construcţie a triunghiurilor, cu precizarea că eu prefer ordinea LLL, LUL, ULU.
- Da, la Identificarea patrulaterelor pe corpuri geometrice sau pe desfăşurări ale acestora (pag.17), dar şi a triunghiurilor. Tocmai ce am propus un opţional de clasa a VII-a cu construcţii de corpuri geometrice din carton.
- Da! (cu mii de mulţumiri!) readucerii sistemelor de ecuaţii în clasa a VII-a, mai ales că au fost aduse doar cu metodele specifice ecuaţiilor (substituţiei şi reducerii), rămânând în clasa a VIII-a metoda grafică (cea care a bulversat zeci de ani elevii la această lecţie).
- Da! (cu mare bucurie) mutării în clasa a VII-a a capitolului despre cerc de la sfârşitul anului (când mulţi nu-l prea mai făceau) în semestrul I. Anul acesta eu am predat Poligoane înscrise în cerc (construcţie, măsuri de unghiuri) şi Lungimea cercului şi aria discului în semestrul I, şi pot depune mărturie că funcţionează foarte bine. De pildă, între cele două teme am calculat aria poligonului regulat cu 12 laturi înscris în cercul de rază r, care este exact 3r2, folosind doar determinări de unghiuri şi cateta opusă unghiului de 30o. La lungimea cercului şi aria discului se pot folosi şi metode aproximative de tip “laboratorul de matematică” (mult sprijinit de dl. acad. Nicolae Teodorescu): determinarea lungimii cercului cu metrul de croitorie, apoi găsirea aproximativă a lui π prin împărţire, respectiv determinarea ariei prin numărarea pătrăţelelor din interiorul cercului pe caietul de matematică sau pe hârtie milimetrică şi apoi împărţirea ariei obţinute la aria pătratului razei. Aceste metode sunt în deplină armonie cu linia prezentului proiect.
- Da! (un DA mare) aducerii inecuaţiilor de la sfârşitul clasei a VIII-a la început, în primul capitol, imediat după intervale.
- Da! (cu evidentă bucurie) precizărilor legate de rezolvarea ecuaţiei de gradul II: prin aplicarea formulelor de calcul prescurtat (pag.26). Ce se întâmplă cu formulele clasice de rezolvare (a,b,c,Δ,x1,2)? Sunt interzise? Le facem în semestrul II? Rămân pentru clasa a IX-a? Trebuie să lămuriţi aceste aspecte, eventual în note de subsol, la fel ca la scrierea măsurii unghiurilor. Eu aş fi mulţumit să rămână în liceu, dar din respect pentru ceilalţi colegi cred că poate fi aleasă varianta cu semestrul II. (ar fi binevenite mai multe astfel de note de subsol, unele dintre ele reparatorii, cum ar fi următoarea: reducerea termenilor opuşi într-o sumă poate fi făcută încă din clasa a VI-a, la numere întregi, nu doar în clasa a VII-a, ca în programa veche; dvs. nu aţi precizat unde se va face pe viitor)
- DA, cu amendament. Susţin aceste elemente de conţinut cu următoarele amendamente:
- Da, readucerii în clasa a V-a a metodelor de rezolvare aritmetică de probleme. În general, doamnele învăţătoare nu prea le ştiu. Am însă îndoieli că profesorii le vor parcurge cât de cât serios. Într-o lume dominată de punerea în ecuaţie, este nevoie de explicaţii serioase, pentru a se înţelege la ce folosesc rezolvările aritmetice.
- Da, readucerii în clasa a V-a a proprietăţilor operaţiei de putere, dar într-o lecţie separată, următoare introducerii puterii. Elevii au nevoie de cel puţin 2 ore (chiar o săptămână) pentru acomodarea cu noua operaţie; ei trebuie protejaţi faţă de profesorii care vin şi “le toarnă” totul din prima zi, fără ca ei, elevii să apuce să se dezmeticească despre ce este vorba. Urmare a acestei “politici de predare” dăunătoare, avem exemplele cu elevii care prin clasa a VII-a spun: puterea este un fel de înmulţire, deci fac înmulţire, adică 23= 6. Un alt argument este că introducerea proprietăţilor puterii din prima lecţie sabotează fixarea acestei noi operaţii în contextul ordinii operaţiilor de ordinele I, II şi III. Ca urmare propun următoarea detaliere (eventual ca observaţie metodologică): Lecţia 1: introducerea operaţiei cu exemple, fără exponentul 0 sau 1, cât şi primele exerciţii simple de ordinea operaţiilor cu toate cele cinci oparaţii. Lecţia 2: lămurirea noţiunii de putere, inclusiv puterea cu exponent 1 sau 0, conexiunea dintre exponent şi numărul zero-urilor la puterile lui 10, cât şi exerciţii de ordinea operaţiilor mai stufoase. Lecţia 3: Proprietăţi ale operaţiei de putere, acestea aducând de obicei o încălcare a ordinii naturale a operaţiilor.
- Da, mutării criteriilor de divizibilitate cu 3 şi cu 9 înapoi în clasa a V-a, cu amendamentul că ar trebui adus şi criteriul cu 25, care este foarte uşor. Criteriul cu 4 eu personal îl voi face oricum ca pereche al lui 25 (la fel cum criteriile cu 2 şi cu 5 sunt în pereche; vezi predarea prin analogie a asemănării triunghiurilor cu congruenţa triunghiurilor, la sugestii metodologice, clasa a VII-a).
- Da studiului mărimilor direct proporţionale şi a celor invers proporţionale, cu următoarea precizare importantă: dacă la proporţionalitate directă avem şir de rapoarte egale, la proporţionalitatea inversă avem şir de produse egale. În acest context vă rog insistent să eliminaţi definiţia cea veche (invers proporţionale înseamnă şir de rapoarte egale cu inversele) care nu mai foloseşte la nimic, doar la bulversat elevii.
- Da construcţiilor geometrice de pătrate şi dreptunghiuri pe baza şirului lui Fibonacci, dar cu amendamentul că va trebui explicat profesorilor ce să facă, altfel colegii vor citi peste acel rând (pag.15). Înţeleg că vorbiţi de desenul de construcţie al spiralei lui Fibonacci; eu îl fac cu elevii, dar câţi îl cunosc?
- Da titlului Noţiuni de trigonometrie, cu rugămintea de inserare a expresiei: rapoarte trigonometrice înaintea enumerării acestora. Din păcate, mulţi profesori care coboară de la liceu la gimnaziu le denumesc funcţii trigonometrice. Ce înţeleg elevii din această denumire? Tot aceşti profesori le dau apoi elevilor şi valorile pentru 0o şi 90o. Ar trebui undeva în programă interzise aceste derapaje.
- NU, cu alternativă. În locul propunerii dvs. vin cu o alternativă care poate oferi atingerea obiectivului propus:
- Scrierea în baza 2 a numerelor în clasa a V-a este prea grăbită, mai ales că majoritatea profesorilor vor face direct scrierea de tipul 1100101. Eu am făcut-o în ultimii ani în recapitularea de la începutul clasei a VI-a sub forma orice număr natural poate fi scris ca sumă de puteri ale lui 2, prezentată ca joc în care elevii trebuiau să găsească puterile lui doi care compun un număr dat. De-abia apoi am dedus scrierea în baza 2.
- La clasa a V-a, în lecţia Înmulţirea fracţiilor, puteri; împărţirea fracţiilor propun mutarea puterii după împărţire, păstrând ordinea naturală a nivelului operaţiilor.
- Este absurd să vorbim la clasa a V-a despre Numere raţionale pozitive, când elevii încă nu au învăţat despre numere negative sau pozitive; sfidează ordinea introducerii noţiunilor fără a avea o motivaţie concretă. Propun să rămânem în clasa a V-a la denumirea de fracţie, cu variantele de fracţie ordinară sau fracţie zecimală, acestea putând fi transformate una în cealaltă, prin semnul de egalitate. Astfel, propun ca noţiunea de număr raţional, cât şi mulţimea ℚ a numerelor raţionale, să fie introduse de-abia la capitolul din finalul clasei a VI-a, parte a procesului foarte bine descris în Note definitorii ale acestei programe (pag. 3).
- Scrierea unui număr natural de două cifre ca produs de puteri de numere prime, poate fi inclusă liniştit în primul capitol din clasa a V-a, mai ales că se precizează prin observare directă. Chiar şi algoritmul de descompunere a numerelor în factori primi este accesibil majorităţii elevilor în clasa a V-a. Acesta este profund conectat cu operaţia de împărţire (o temă de bază a sem.I din clasa a V-a), cu operaţia de putere şi cu criteriile de divizibilitate cu numerele 2, 5 şi 3, pentru care reprezintă o bună aplicaţie.
- Elevii pricep foarte greu scrierea divizibilităţii cu bară verticală (ex. 3|51, la pag.15). Pentru divizibilitate ar trebui reintrodus oficial semnul
 care conectează în mintea elevului cu semnul împărţirii (un punct în plus înseamnă împărţire exactă), dar rămâne pe calapodul de gândire obişnuit (numărul mare este divizibil cu numărul mic, evitând inversarea cerută de scrierea cu bară).
care conectează în mintea elevului cu semnul împărţirii (un punct în plus înseamnă împărţire exactă), dar rămâne pe calapodul de gândire obişnuit (numărul mare este divizibil cu numărul mic, evitând inversarea cerută de scrierea cu bară). - Nu este precizat, aşa că ar trebui explicit interzisă definirea tradiţională a interiorului unui unghi, cea prin intersecţia de semiplane. Profesorii trebuie doar să coloreze sau să haşureze interiorul unghiului; exteriorul vine de la sine înţeles, aşa că, folosind intuiţia copilului, nici n-ar mai trebui prezentate; oricum, la ce foloseşte exteriorul unghiului?
- Folosirea, introducerea ideii de demonstraţie geometrică doar pe cazul unei singure matode, anume a metodei triunghiurilor congruente, în clasa a VI-a este periculoasă pentru formarea gândirii elevului: mulţi elevi reacţionează ulterior la probleme ce necesită alt tip de argumentaţie, forţând pseudo-demonstraţii fără sens care au forma unicei demonstraţii învăţate, cea cu congruenţa de triunghiuri; iar când le spui că au greşit se uită năuciţi şi nu înţeleg ce se întâmplă. Elevii trebuie să cunoască şi alte demonstraţii în paralel. Eu m-am concentrat din start la câteva exemple de demonstraţii cu unghiuri.
- Demonstraţiile prin metoda triunghiurilor congruente în cazul figurilor axial-simetrice nu au sens în mintea elevului începător, minte care vede intuitiv că cerinţa este îndeplinită prin simetria figurii. Introducând criteriul ne-simetricităţii figurii, rămân foarte puţine probleme pe care elevul să înveţe această metodă. Problemele cu congruenţă în figuri cu cerc mai pot ajuta un pic, dar nu prea mult. De-abia când apar şi patrulaterele, cantitatea de aplicaţii nesimetrice creşte la un nivel mulţumitor.
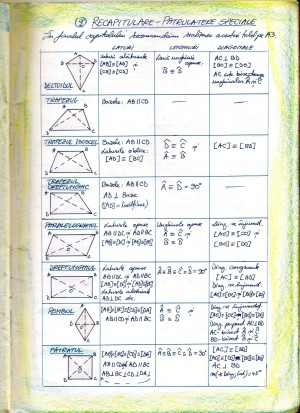
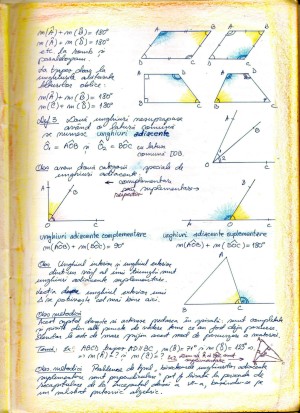
- Păstrarea capitolului despre patrulatere în clasa a VII-a are o serie de dezavantaje majore. Pe lângă conexiunea cu precedentul aliniat, este evident că aplicaţiile la primele tipuri de demonstraţii (inclusiv cele cu unghiuri) sunt foarte restrânse doar în triunghiuri (triunghiul este o figură săracă în aplicaţii simple dar nesimetrice). Readucerea capitolului despre patrulatere în clasa a VI-a ar rezolva toate cele expuse. Patrulaterele s-ar putea parcurge foarte uşor prin cunoaşterea intuitivă a proprietăţilor acestora, prin construcţi detaliate în diferite cazuri (o bogăţie de exemple, aliniat cu principiul mai sus menţionat pentru clasa a VI-a), dar şi prin primele exemplificări ale conexiunilor demonstrabile între proprietăţile acestora (multitudinea de teoreme directe şi reciproce). În plus, am scăpa astfel de schizofrenia manifestată actual când le dăm elevilor o figură formată din două triunghiuri, dar ne facem că nu ştim că acela este de fapt un patrulater. Dau aici exemplul trapezului de la EN Cl.a VI-a din urmă cu trei ani, care era prezentat ca o combinaţie de două triunghiuri, şi la care copiii s-au chinuit foarte mult. Dacă ar fi cunoscut trapezul dreptunghic, lucrurile ar fi fost mai clare. Mai dau un exemplu: noţiunile de unghiuri complementare, respectiv suplementare, se înţeleg mult mai bine într-o prezentare unitară, după patrulatere, cu exemple clare din triunghiuri şi patrulatere. Anexez prezentei scrisori deschise scanarea notiţelor personale (din 2011) cu capitolul despre patrulatere pentru finalul clasei a VI-a, redactat conform principiilor predării intuitive specifice acestei clase. Precizez că tema liniilor mijlocii o las totuşi pentru clasa a VII-a când, la începutul semestrului I, pe post de “recapitulare şi completări” atacăm serios diversele demonstraţii geometrice. Pentru elevii buni acestea devin una din temele principale de lucru în clasa a VII-a.
- Nu, introducerii din primul capitol din clasa a VII-a a numerelor reale. Elevii au nevoie să petreacă o vreme în calculul aproximativ al diferitelor mărimi care nu au rezultat întreg. De pildă, calculul înălţimii şi a ariei unui triunghi echilateral, dar şi lungimea şi aria cercului, au o puternică componentă practic-aplicativă de aproximare. Nimeni nu înţelege cât este lungimea unei borduri de 25π m din jurul unui sens giratoriu, aşa că apelăm la calculul aproximativ 25 ∙ 3,14 ≅78,5m. Din câte ştiu, în vest numerele iraţionale ca atare apar doar în liceu. Eu am împărţit clasa a VII-a astfel: în semestrul I dăm rezultate aproximative aritmetice (atât la cerc, cât şi teorema lui Pitagora – vezi primul comentariu de la categoria 4), iar în semestrul II trecem la calcul algebric, cu numere iraţionale, atât la algebră, cât şi la geometrie. Astfel împăcăm ambele direcţii de gândire matematică, studiind în semestrul I doar rădăcina pătrată, iar în semestrul II noţiunea de număr real.
- Nu! acelei lecţii stupide de la capitolul despre cerc din clasa a VII-a despre proprietăţi: la arce congruente corespund coarde congruente şi reciproc, diametrul perpendicular pe o coardă, arce cuprinse între coarde paralele, coarde egal depărtate de centru. Acestea reprezintă doar drumul segmentat pentru demonstrarea faptului că tangenta la cerc este perpendiculară pe raza în punctul de contact. Dar această demonstraţie nu se predă în şcoli, deci nici teoremele pregătitoare nu-şi au sensul. Acestea doar îi chinuie pe elevi, care nu pricep ce vrea profesorul. Nici profesorii nu prea au probleme aplicative cu sens la această lecţie. Peste aceste teoreme se poate sări simplu, trecând direct la observarea perpendicularităţii tangentei pe rază. În schimb, există deosebite aplicaţii la “teorema ciocului de cioară” (cele două tangente dintr-un punct la un cerc sunt congruente), bine apreciate de către elevii buni. Propun reintroducerea în materie a acestei teoreme. Dacă tot am ajuns la propuneri, permiteţi-mi încă una: în contextul reintroducerii cercului în clasa a VI-a, se poate demonstra direct la nivelul acestei clase că triunghiul înscris în semicerc este dreptunghic (în conexiune cu “mediana pe ipotenuză”).
- Nu (un Nu conştient şi experimentat) păstrării ordinii lecţiilor de geometrie din clasa a VIII-a. La această formă s-a făcut doar “o jumătate” de pas în sensul folosirii intuiţiei naturale a elevilor (intuiţia este activă în continuare; folosirea ei nu trebuie interzisă cu avansarea în vârstă; mai ales la elevii slabi intuiţia rămâne în continuare principala cale de acces la cunoştinţe). La ce ajută prezentarea corpurilor de la lecţia a doua, dacă elevii nu fac apoi mai nimic cu aceste corpuri? În tot semestrul I vin doar lecţii grele şi abstracte, nimic pentru elevii slabi care ar vrea şi ei să calculeze o arie, să aplice teorema lui Pitagora şi o formulă. În locul acestei ordini a lecţiilor vă propun următoarea ordine, în care predau cu rezultate foarte bune de aproape 20 de ani. Astfel: Capitolul I – Corpuri (I): Cubul, paralelipipedul dreptunghic, prismele, piramidele şi tetraedrul, cu reprezentare, elemente, arii şi volum, totul pe baze intuitive (la apotemă nu este nevoie de T3⊥ pentru că avem triunghiuri isoscele, iar înălţimea se înţelege foarte uşor). Capitolul II – Teoreme în spaţiu: Paralelism, perpendicularitate, T3⊥, unghi diedru . Capitolul III – Corpuri (II): Trunchiuri de piramidă, corpuri rotunde, cu reprezentare, elemente, arii şi volum. Astfel, elevii slabi primesc din start material de lucru, iar elevii buni, cu o scurtă întârziere primesc şi ei “hrană” pe măsura lor. Nu mai intră T3⊥ până la teză, dar până la sfârşitul primului semestru, până la olimpiadă şi simulare sigur se termină tot capitolul II.
- NU, cu avertisment! Consider că introducerea acestor elemente prezintă un mare risc, pe care îl voi expune:
- Mutarea teoremei lui Pitagora în clasa a VI-a prezintă un multiplu pericol major. Ar mai avea oarecare sens dacă am parcurge o primă parte de rădăcină pătrată la nivel intuitiv aritmetic (cum era prin anii ’90). Aceasta însă lipseşte. Mă îngrozesc de felul cum profesorii vor turna în elevii de clasa a VI-a elemente din arsenalul cunoscut din clasa a VII-a legat de teorema lui Pitagora. Cum vor arăta subiectele de la EN a clasei a VI-a incluzând numerele pitagoreice? În plus, în acest mod teorema lui Pitagora este coborâtă la nivelul banal de observaţie, subminând ideea unei demonstraţii pe viitor. Teorema cu cele mai multe demonstraţii din toate câte sunt, nu va mai avea nevoie de demonstraţie în mintea elevilor. Cea mai importantă teoremă din toate timpurile este redusă la nivelul unei reţete. Totuşi vin cu o propunere de remediere. În ultimii 15 ani am predat teorema lui Pitagora în semestrul I din clasa a VII-a, într-un capitol complex, format din trei părţi: 1) rădăcina pătrată; 2) ariile patrulaterelor şi a triunghiurilor; 3) Teorema lui Pitagora (demonstrată prin arii; există chiar două demonstraţii, din care una foloseşte şi congruenţa triunghiurilor), cu aplicaţii în calculul perimetrelor şi al ariilor. Mutarea respectivă este deosebit de benefică atât elevilor slabi, cât şi elevilor buni. În plus rezolvă şi o problemă de fond a acestei mutări (neprecizată în proiect dvs.), anume că parcurgerea acestei teoreme mai repede este cerută de profesorii de fizică, care altfel o explică ei elevilor înaintea noastră. Revenind la demonstrarea teoremei lui Pitagora, menţionez că eu parcurg cu elevii în clasa a VII-a cel puţin trei demonstraţii diferite, la lecţiile corespunzătoare (pe lângă demonstraţia cu arii amintită şi demonstraţia cu teorema catetei arhicunoscută, mai aleg şi o demonstraţie pe bază de arii şi formule de calcul prescurtat (în conexiune cu următorul punct).
- Neintroducerea formulelor de calcul prescurtat în clasa a VII-a este o mutare inexplicabilă, un deja vú ce aminteşte de conul de penumbră în care au fost înghesuite sistemele de ecuaţii în ultimii ani. Elevii au nevoie de o perioadă de jumătate de an în care să se obişnuiască cu noua mişcare matematică, cu noul raţionament specific calculului prescurtat, astfel încât să le poată folosi eficient în semestrul I din clasa a VIII-a. Mutarea propusă va bulversa din nou o mare parte din materia de studiat, la fel cum a făcut-o şi mutarea sistemelor din clasa a VII-a în finalul clasei a VIII-a. Formulele de calcul trebuie să apară în clasa a VII-a, chiar şi dacă apar numai într-un singur sens. Astfel, elevilor slabi eu le cer doar direcţia de explicitare, de tipul (3x + 1)2= 9x2 + 6x + 1, nu şi direcţia inversă de transformare în produs. Legat de acest subiect am încă o propunere: personal, accept ideea unei “fobii” oficiale faţă de cuvântul polinom (dezvoltată în gimnaziu la începutul anilor ’90 pe vremea renumitelor probleme de divizibilitate cu teorema lui Bezout), dar nu le putem spune la nesfârşit Operaţii cu numere reale reprezentate prin litere (etc.). (clasa a VIII-a, pag.28) Aşa cum la expresiile cu fracţii s-a acceptat noţiunea de Fracţii algebrice, tot aşa propun ca la fostele polinoame să folosim noţiunea de Sume algebrice.
Închei cu speranţa sinceră că se vor dovedi de folos cât mai multe din observaţiile făcute. Totodată, precizez că stau la dispoziţia dvs. pentru eventuale lămuriri pe care le-aţi considera necesare.
Titus Grigorovici
Profesor Şcoala Waldorf Cluj-Napoca











In articolul dumneavoastra din octombrie 2019 , doua greseli impardonabile pentru un doritor sa invete pe altii :
– tabelele cu impartiri care au inundat “piata” nu sunt (o) tabla a impartirii! Nu exista o tabla a impartirii!!! Exista doar o tabla(patratica) a inmultirii , atribuita lui Pitagora,tabla dupa care se fac /se invata si impartirile!!!
– reprezentarea prin segmente a numerelor cunoscute si necunoscute si arelatiilor dintre ele se numeste corect :metoda figurativa! Metoda grafica – ati pomenit de ea- se invata incepand cu clasa a 7-a! Pentru lamuriri consultati singurul ghid aprobat de M.E. Matematica Ghidul invatatorului, editura Lucian.
–
Observații la începutul anului 3 (după noua programă) 🙁
Mulțimi, segmente, unghiuri, divizibilitate și ecuații -clasa a VI-a.
Am stat mai bine de o lună la mulțimi, având o clasă medie, care nu a făcut nici o conexiune cu noțiunile predate în clasa a V-a.
La segmente și unghiuri am luat-o de la început ( sunt mulțimi de puncte, cu notații și tot meniul asociat, nu-i așa?), fără posibilitatea de a rezolva civilizat multitudinea de ecuații aferente.
Metodele aritmetice erau foarte bine predate de către învățători, acceptate și însușite de către elevi (fără exagerări, sume Gauss sau metoda ”algebrică”). Acum elevii intră în gimnaziu cu un bagaj matematic … extrem de modest, dar cu EN II și cu EN IV trecute cu succes!
Teorema lui Pitagora a devenit șarpele acestei programe.
Materia clasei a VII-a este extrem de lejeră, avem timp până și pentru jocuri didactice, În clasele V-VI nici vorbă de așa ceva (goana după olimpici).
Greul a rămas … pentru clasa a VIII-a.
Despre evaluare și mai ales despre Evaluarea națională din 2021 nu vorbește nimeni. Curriculum fără evaluare … nu există.
Poate nu am înțeles eu prea bine noua programă, dar am pierdut o groază de timp ! … A, peste trei săptămâni dăm teza. Atât.
Bravo, cu felicitări!