Category: Metodică

De când am pornit acest blog am scris de câteva ori despre figura geometrică cu trei pătrate construite pe laturile unui triunghi dreptunghic şi despre faptul că aceasta prezintă într-o formă deosebit de intuitivă Teorema lui Pitagora. De pildă, în luna mai 2018, în postarea despre cum mi-am pus faianţa în baie, am arătat cum am încercat să evoc în propria-mi casă amintirea din copilărie despre figura geometrică cu cele trei pătrate, figură ce era zugrăvită pe un perete al holului de intrare în apartamentul unde am locuit până în clasa a VI-a, acasă în Oraşul Victoria. Foarte interesant, cât de pregătit eram eu de pe atunci pentru Teorema lui Pitagora în clasa a VI-a.

Reluarea temei cu ajutorul ciocolăţilor pătrate Ritter Sport nu reprezintă în acest sens o simplă fixaţie, o ciudăţenie personală, ci răspunde unei necesităţi de moment în sensul sprijinirii profesorilor ce vor avea de predat în finalul clasei a VI-a Teorema lui Pitagora începând de anul acesta. Acolo este stabilită prin programă, explicându-ni-se că trebuie să o predăm fără demonstraţie, explicată prin verificări de triplete de numere pitagoreice, doar pentru a putea ajunge cât mai repede la determinarea lungimii folosind pătrate perfecte (din nou citatele sunt preluate înclinat din programa de matematică – clasele V – VIII, pag. 16). Trebuie (!) să facem acest lucru pentru a ne asigura că le-o predăm elevilor NOI, PROFESORII DE MATEMATICĂ, cea mai importantă teoremă din gimnaziu, probabil chiar cea mai renumită din toate timpurile, astfel încât să nu apuce să le-o arate elevilor colegii profesori de fizică, doar pentru că lor le-o trebuie în toamna clasei a VII-a.

OK, foarte bine aşa, dar care-i diferenţa? Că le-o arată ei superficial sau le-o arătăm noi superficial înaintea lor, tot superficial se numeşte. Am arătat în prima parte cum putem însă aduce această teoremă într-o formă de minimă “demonstrare”, o formă de justificare intuitivă, scoţând-o astfel din starea de HOCUS-POCUS de neînţeles spre care ne direcţionează noua programă.

După cum am mai spus, sunt foarte mulţi cei care nu cunosc figura cu triunghiul dreptunghic şi pătratele construite în exterior pe laturile sale, care nu o asociază cu Teorema lui Pitagora. Se întâmplă asta pentru că respectiva figură a fost exilată din manuale începând cu reforma din 1980, demonstrarea teoremei făcându-se doar pe baza teoremei catetei obţinută prin asemănarea triunghiurilor, respectiv datorită faptului că în textul teoremei s-a pus accentul doar pe aspectul de putere a doua a lungimii unei laturi, eliminându-se din discuţie ideea de arie a unui pătrat. Interesant este aici următorul aspect: dacă, în justificările cu pătratele construite pe laturile triunghiului, legătura dintre unghiul drept şi relaţia între cele trei pătrate este destul de evidentă pentru “ochiul începător” al elevilor, în demonstraţiile care folosesc doar lungimile laturilor, adică numerele la puterea a doua, legătura dintre cele două părţi ale Teoremei lui Pitagora se pierde pentru cei mai mulţi elevi.

S-a mers astfel în ultimii aproape 40 de ani doar pe abordarea aritmetică, eliminându-se cu totul forma geometrică, formă care aducea o foarte vizibilă reprezentare grafică a fenomenului numeric pe care se bazează Teorema lui Pitagora. Oare ce se întâmplă în alte părţi legat de aspectele discutate? În plimbările mele pe internet am găsit diferite poze care aduc în discuţie situaţia cu pătratul ipotenuzei care este cât suma pătratelor catetelor, exemplificată pe cazul triunghiului de laturi (3, 4, 5). Iată două mai interesante dintre acestea, poze care arată cât de cunoscută este de fapt imaginea respectivă:

La ce sunt bune toate acestea – veţi întreba – de vreme ce autorii noii programe nu au acordat nici măcar o minimă atenţie ideii de “demonstraţie” a teoremei. Noi de ce să ne stresăm când ei tocmai au deschis cutia Pandorei, spunând lejer că se poate “fără demonstraţie” la cea mai mare teoremă din toate timpurile?! (conform programei, a doua trecere pe la Teorema lui Pitagora, de data asta cu demonstraţie, se face de abia peste un an, undeva în finalul clasei a VII-a).

Se vede aşadar – pentru orice matematician responsabil – că discuţia despre prezentarea Teoremei lui Pitagora în finalul clasei a VI-a este una importantă, mai ales prin prisma justificării accesibile a acesteia pe baza însumării ariei pătratelor catetelor pentru a obţine echivalarea ariei pătratului ipotenuzei. Până acum am discutat despre prezentarea unor situaţii sub formă concretă (cine mai găseşte şi altele în afară de ciocolată, “LEGO” sau roşii?) sau de imagini aduse ca poze ori prezentate digital, imagini care ar trebui desigur să se concretizeze şi ca figuri geometrice pe tablă (profesorul de mate trebuie să fie conştient de importanţa unui astfel de demers). Cu alte cuvinte, am discutat doar despre ce ar trebui să facă profesorul în faţa clasei pentru a prezenta această teoremă cât mai just.

Cred că ar fi cazul să ne îndreptăm atenţia şi asupra felului despre cum ajung aceste desene în caietele elevilor? (aspecte despre care desigur că programa cea nouă nu ne vorbeşte). Nu trebuie făcute multe desene. Cum am precizat în finalul postării despre folosirea ciocolatei, este vorba de puţine figuri geometrice, dar acestea ar trebui să fie cât de cât coerent şi corect realizate în caiete. Indiferent de câtă experienţă are o clasă în realizarea figurilor geometrice (din câte văd în jurul meu, nu prea se lucrează în acest sens), sunt şanse mari ca mulţi elevi să nu reuşească acest desen, pentru că este vorba de construirea unuia sau a două pătrate poziţionate oblic faţă de aliniamentul şi liniatura caietului de matematică. Şi atunci ce facem?

Eu cred că există două direcţii de acţiune. Prima ar fi ca elevii să decupeze pătratele (anterior colorate) de pe o altă coală de hârtie (tot cu pătrăţele) şi să le lipească corect asamblate în caietul de clasă la locul potrivit în cadrul lecţiei. Aceasta ar fi varianta uşoară, pentru că nu implică construcţii geometrice foarte abile. Dar pentru asta trebuie să fim dispuşi la transformarea unui sfert de oră de matematică într-o parte manufacturieră, pentru care elevii trebuie să aibă la ei lipici şi foarfecă. Desigur, le-o putem da şi ca temă, dar în acest caz eu nu garantez pentru ce se va găsi în unele caiete.

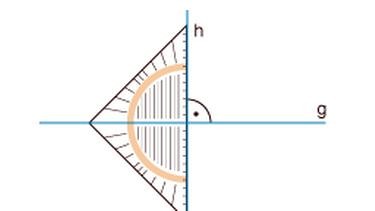
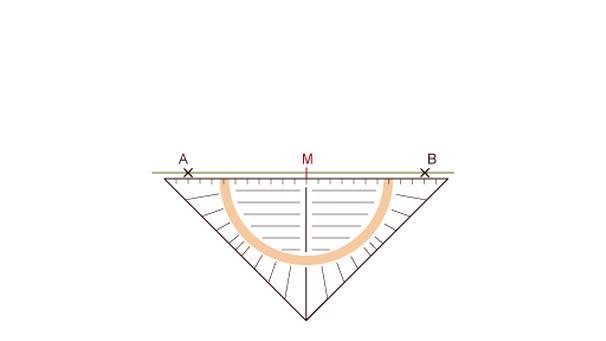
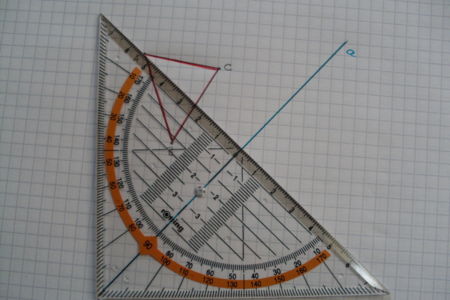
O a doua direcţie de reprezentare ar fi desenarea figurii geometrice cu instrumente pe caiet. În acest moment apare ideea de a alege între cele două posibile variante de poziţionare a triunghiului dreptunghic: cu ipotenuza drept bază (aşa cum am prezentat-o în imaginile cu ciocolata sau cu faianţa) sau cu o catetă drept bază (aşa cum apare în pozele cu piesele “LEGO” sau cu roşiile cherry). În varianta cu ipotenuza ca bază vom avea de construit două pătrate înclinate pe laturile oblice, pe când în varianta cu o catetă ca bază (să alegem cateta cea mare) vom avea de construit doar un pătrat pe o latură oblică (cel de pe ipotenuză). Este evident că a doua variantă este preferabilă din acest punct de vedere.

Un aspect mai trebuie evidenţiat aici, anume că la triunghiul (3, 4, 5) figura cu pătrăţele este destul de mică, dar poate fi uşor dublată prin trecerea la altă unitate de măsură, anume la cm². Dimpotrivă, la triunghiurile (6, 8, 10) sau (5, 12, 13) figurile în pătrăţele sunt clar preferabile pentru a încăpea pe pagina de caiet. Dacă vrem să le punem pe toate trei triunghiurile alăturat, pentru a exemplifica (bio)diversitatea acestora, atunci vom alege desigur pătrăţelul caietului de matematică drept unitate de măsură.

Dacă încercăm să analizăm şi mai profund aceste două variante de realizare a figurii – poziţionând ipotenuza sau o catetă drept bază – atunci ajungem să descoperim aspecte de-a dreptul surprinzătoare.

Construcţia figurii cu o catetă drept bază ne “îndrumă” spre cazul de construcţie LUL în varianta sa CC (catetă-catetă cu unghiul drept între acestea). Putem să ne imaginăm aici de pildă cateta de 4 ca bază şi cateta de 3 ca înălţime, pătratele acestora fiind desenate cu laturile orizontale sau verticale exact pe liniile de pe caietul de matematică. În acest caz lungimea ipotenuzei de 5 apare ca “probă” a construcţiei.

Dimpotrivă, construcţia figurii cu ipotenuza drept bază ne “îndrumă” spre cazul de construcţie LLL: latura de 5 ca bază şi laturile de 3 şi 4 ca laturi oblice construite cu compasul. În acest caz verificarea corectitudinii situaţiei se face cu un echer care va verifica unghiul drept.

Cu alte cuvinte, mai elevat spus, adică într-un limbaj mai potrivit clasei a VII-a, în cazul construcţiei triunghiului dreptunghic cu laturile de (3, 4, 5), varianta de construcţie cu cateta ca bază corespunde Teoremei directe a lui Pitagora; dimpotrivă, varianta de construcţie cu ipotenuza ca bază şi catetele oblice, dar de lungimi date, corespunde mai degrabă Teoremei reciproce a lui Pitagora.

În final îmi permit să vă aduc şi o mică imagine din pedagogia alternativă Waldorf, care sărbătoreşte anul acesta 100 de ani de la înfiinţarea primei astfel de şcoli la Stuttgart în Germania (septembrie 1919). Rudolf Steiner, întemeietorul acestei şcoli, a cuprins pentru clasa a V-a şi o materie numită Desen geometric cu mâna liberă, în care elevii trebuiau să parcurgă în formă de desen principalele figuri geometrice, ajungând până la Teorema lui Pitagora, cel puţin în cazul triunghiului dreptunghic isoscel. De-a lungul anilor, dascălii Waldorf au încercat să găsească căi de parcurgere a acestei materii. Pe caietul de matematică putem foarte uşor desena o astfel de figură pentru că laturile oblice sunt în acest caz diagonale ale pătrăţelelor, fiind înclinate la 45^o faţă de liniatură. După ce construim figura, împărţim pătratele de pe catete cu câte o diagonală, iar pătratul ipotenuzei cu ambele diagonale, relaţia din Teorema lui Pitagora devenind astfel evidentă.

În acest sens vă prezint şi o imagine cu o dublă caricatură din 1886, din Foaia volantă de München, cu Pitagora înainte şi după descoperirea renumitei teoremei denumită după el, în cazul triunghiului dreptunghic isoscel. Nu cred că Steiner a avut aşa ceva în gând atunci când a spus cele de mai sus, dar această caricatură ne oferă măcar o oarecare imagine a spiritului acelor vremuri în legătură cu subiectul nostru. CTG

P.S. “Ameninţarea” cu cutia Pandorei legată de lipsa unei demonstraţii a fost desigur o exagerare, mai degrabă o “figură de stil” menită să dea un aer de opoziţie. Realitatea este că în matematica gimnazială există multe puncte unde nu prea le explicăm elevilor de unde vin lucrurile învăţate.

Jocul din copilărie “de-a hoţii şi vardiştii” se numeşte în matematica pură “de-a axiomele şi teoremele”. Însă în matematica şcolară mai apar şi alţi factori decisivi, ca doi arbitri pe care i-am putea denumi accesibilitate şi intuitivitate. Aceştia interferează în procesul de stabilire a materiei de predat, eliminând din jocul pur “de-a axiomele şi teoremele” diferite pasaje, ca fiind prea “violente”, adică inaccesibile minţii elevilor. Haideţi să trecem în revistă câteva astfel de momente, în care demonstrarea paşilor parcurşi este “împinsă sub preş”, omisă sau doar mimată.

Dintre cele mimate îmi vin acum în minte două momente. Primul ar fi Teorema lui Thales, care este oarecum pregătită prin Teorema paralelelor echidistante. Aceasta însă poate duce la justificarea primeia doar în cazul unui raport raţional; situaţia iraţionalităţii rămâne “în aer”, fiind preluată însă în mod inconştient de intuiţia elevilor (aşa se întâmplă şi pentru numere iraţionale). Un alt caz, chiar mai enervant, îl reprezintă teorema care afirmă că tangenta la un cerc este perpendiculară pe raza dusă în punctul de contact. Aceasta nu primeşte o demonstraţie, dar elevii sunt plictisiţi de către toţi profesorii şi de către toate manualele cu câteva teoreme premergătoare pe drumul unei demonstraţii: arce cuprinse între coarde paralele etc. Acestea, la rândul lor, nu au mai deloc aplicaţii (în mod similar cu teorema paralelelor echidistante), dar toată lumea le face.

Dintre cele prezentate fără demonstraţie mă gândesc la următoarele. Primul exemplu ar fi metoda triunghiurilor congruente: dintre cele trei cazuri, unul era considerat axiomă iar celelalte erau demonstrate din acesta. Când am început noi să predăm şi trebuia să ne dăm definitivatul era încă la modă acest subiect: care este axioma şi cum era demonstraţia aia prin reducere la absurd? Un alt exemplu în acest sens, faţă de care nimeni nu face “mare caz” este formula pentru volumul piramidelor: de ce este acolo supra 3? Dacă la aria triunghiului se poate uşor explica de ce este supra 2, la volum lucrurile stau mult mai greu. Cât despre formulele sferei în acest context, am vorbit cu altă ocazie. Mai dau încă un exemplu, din aritmetico-algebră: de unde vine algoritmul de extragere a rădăcinii pătrate? De ce se face în acest mod?

Analizând însă toate aceste exemple, vedem că ele au fost eliminate din predare sau nici măcar nu au fost introduse, deoarece demonstraţia respectivă a fost considerată (din start sau ulterior) mult prea dificilă pentru mintea gimnazială a elevilor. Vedem deci că nu este nimic neobişnuit în a li se da elevilor o teoremă fără justificare. Consider însă că Teorema lui Pitagora poate fi justificată într-un mod intuitiv accesibil prin ariile pătratelor celor trei laturi ale triunghiului dreptunghic, aşa că prezentarea acestei teoreme fără nici măcar o minimă justificare poate fi liniştit considerată drept o gafă de predare.

Îmi permit aici şi o scurtă observaţie nematematică de final: cu scuzele de rigoare vreau să precizez că sunt conştient că folosesc un limbaj care pentru răgăţeni ar putea suna în anumite momente a regionalism, de pildă în cazul pluralului cuvântului ciocolată (ciocolăţi în loc de ciocolate). Prefer varianta ardelenească din două motive: în primul rând consider că dă textului o culoare specifică Clujului, oraş unde îmi desfăşor activitatea; în al doilea rând, folosind exprimările uzuale din această zonă, îmi permit să stau în “zona de confort” din punct de vedere lingvistic, fapt care mă ajută să mă concentrez mai bine asupra subiectelor propuse. Sper că cititorii pot trece peste aceste impedimente, reuşind la rândul lor să se concentreze asupra gândurilor exprimate în aceste eseuri.

De curând mi-am dus la îndeplinire o dorinţă mai veche, anume de a realiza din ciocolăţi Ritter Sport figura geometrică ce prezintă Teorema lui Pitagora cu pătratele laturilor sale în exteriorul triunghiului (3, 4, 5). Am încercat diferite variante pentru o poză cât mai sugestivă şi mâncând cu această ocazie destul de multă ciocolată. Pentru a se înţelege cât mai clar şi a ajuta la exprimarea în cazul viitoarelor folosiri a imaginii la clasă am ales până la urmă ciocolăţi de culori diferite (neagră, albă şi cu lapte). Iată ce a ieşit:

Odată vizualizată imaginea pe ecran, am realizat avantajul uriaş al acestei poze în contextul includerii Teoremei lui Pitagora în finalul clasei a VI-a pe noua programă, fără demonstraţie, explicată prin verificări de triplete de numere pitagoreice, doar pentru a se putea ajunge cât mai repede la determinarea lungimii folosind pătrate perfecte (pasajele prezentate înclinat sunt preluate din programa de matematică – clasele V – VIII, pag. 16).

Pentru cei care încă n-au înţeles, la nivelul conducerii matematicii şcolare s-a ajuns la concluzia că Teorema lui Pitagora trebuie predată înainte de începutul clasei a VII-a, pentru că altfel profesorii de fizică de la grupele de excelenţă (şi nu numai) încep să le-o arate oricum elevilor în toamnă, pentru că au nevoie de ea în sezonul de olimpiade din primăvară, dovedind astfel o acută durere în cot faţă de minimele nevoi de rigurozitate ale matematicii.

Aşadar să le dăm elevilor Teorema lui Pitagora fără nici măcar o minimă justificare! Eu nu sunt de acord cu aşa ceva, şi asta pentru că legătura realizată prin Teorema lui Pitagora (directă sau reciprocă) între proprietatea unui triunghi de a avea un unghi drept şi ciudata egalitate între puterile “a doua” ale lungimilor laturilor sale, această legătură este una lipsită total de evidenţă. Cu alte cuvinte, noua programă ne cere să dăm cea mai mare teoremă din toate timpurile doar ca un fel de reţetă gen hocus-pocus şi gata.

Acest aspect de totală ne-evidenţă de care vorbesc, era evidenţiat în stilul lor specific chiar şi de preoţii de Egiptul Antic. Iată cum prezentau ei asocierea între triunghiul dreptunghic şi ciudata egalitate între puterile a doua ale triunghiului (3, 4, 5). În mistica vremii aceştia considerau numerele pare ca femeieşti iar numerele impare ca bărbăteşti (6 = 3 + 3 iar 7 = 3 + 1 + 3). În egalitatea 3² + 4² = 5², numărul 3 era considerat zeul  Osiris, 4 era zeiţa Isis, iar 5 era copilul lor Horus. Cu alte cuvinte, adunarea între 3 şi 4 care dă 5, prin intermediul ridicării la pătrat era considerată o adunare divină. În limbajul nostru, pentru a nu deveni mistici, putem spune că legătura dintre unghiul drept al unui triunghi şi laturile sale care să respecte o egalitate de felul 3² + 4² = 5² este o legătură uluitoare, total ne-evidentă.

Situaţia de lipsă totală a unei minime evidenţe se păstrează atâta vreme cât păstrăm folosirea cuvântului “pătrat” doar pentru “puterea a doua”. Însă imediat ce acceptăm folosirea cuvântului “pătrat” cu sensul său iniţial, de figură geometrică, respectiv înţelegând că vorbim de aria sa, lucrurile capătă brusc sens, cel puţin în cazul triunghiurilor cu laturi de lungimi întregi. Din păcate însă, acest aspect a fost neglijat total de către autorii programei noi la mutarea Teoremei lui Pitagora în clasa a VI-a.

Văzând minunata poză de mai sus cu pătratele (având incontestabil unghiuri drepte), se observă automat că laturile celor două pătrate mai mici sunt aliniate perfect, arătând astfel evidenţa unghiului drept al triunghiului cuprins între cele trei pătrate. Moment în care m-am gândit să refac figura şi cu alte numere, adică cu alte pătrate decât cele de (3, 4, 5). Zis şi făcut, şi iată ce a ieşit:

Analizând cele trei poze în comparaţie cu prima se poate vedea clar că la acestea triunghiul cuprins între cele trei pătrate nu mai este dreptunghic, pentru că cele două pătrate mai mici nu au laturi în prelungire. Facem în paralel o verificare de ordin aritmetic: 2² + 3² < 4² (4 + 9 < 16) şi 3² + 4² < 6² (9 + 16 < 36) pentru situaţiile cu triunghi obtuzunghic, respectiv 4² + 5² > 6² (16 + 25 > 36) pentru o situaţie cu triunghi ascuţitunghic. Aceasta ne creează un tablou mai larg şi mai clar: a² + b² < c² indicându-ne un triunghi obtuzunghic, pe când a² + b² > c² (c fiind latura cea mai lungă) corespunzând unui triunghi ascuţitunghic, situaţia de trecere între cele două variante, reprezentată printr-o egalitate, adică atunci când a² + b² = c², ne indică evident un triunghi dreptunghic. Clar? Clar!

Cred că o astfel de succesiune de imagini poate aduce o destul de bună legătură în mintea elevilor de clasa a VI-a, între ideea de triunghi dreptunghic şi egalitatea divină între “pătratele laturilor” sale. Desigur că putem confecţiona şi nişte cartoane împărţite în pătrăţele de aceeaşi mărime, pătrate cu laturi de 2, 3, 4, 5, 6, 7 etc. cu care să putem experimenta ceva mai mult ca în situaţiile sus prezentate. Confecţionând până la pătrate de 10 am putea arăta şi următoarea situaţie de egalitate pentru triunghiul (6, 8, 10) obţinut prin amplificarea primului, cunoscut şi ca triunghiul egiptean. Dacă am avea pătrate până la 13, am putea să le arătăm un triunghi dreptunghic nou, triunghiul (5, 12, 13), care nu derivă din amplificarea celui egiptean.

Pe de altă parte, seria redusă până la 6, dar din ciocolăţi Ritter Sport este mai atractivă (gustoasă), fiind destul de clară şi edificatoare pentru copii (o astfel de variantă, cu ciocolăţi achiziţionate din fondul clasei, se finalizează şi cu un mic festin dulce pentru elevi, legându-le definitiv în amintire Teorema lui Pitagora de o senzaţie pozitivă). Găsind prin magazine doar ciocolăţi cu latura de 4 sau 6, am decis să tai din acestea pentru a obţine pătrate cu latura de 2, 3, respectiv de 5. Ciocolăţile Ritter Sport au ajuns o prezenţă obişnuită şi în România. La nemţi sloganul lor este QUADRATISCH. PRAKTISCH. GUT, care în traducere liberă înseamnă pătratic – practic – bun (traducerea imprimată în engleză pe unele ambalaje este parţial diferită). Pentru cei interesaţi de detalii gustoase (adică pe post de bibliografie), am folosit următoarele sortimente: white + crisp (cea albă), nugat praline (cea cu culoare de ciocolată de lapte) şi dark chocolate – halbbitter (cea mai întunecată).

În urmă cu un an, când am avut ideea aceasta, am căutat imediat şi pe internet. Nu se putea ca să nu fi avut altcineva ideea respectivă până atunci. Şi într-adevăr, am găsit poze cu Pitagora şi Ritter Sport, dar cu nişte ciocolăţele împachetate câte un pătrăţel individual (într-adevăr, dacă vrei să o faci la clasă, este mult mai igienic aşa). Deşi în acest caz pătratul este de obicei deformat în dreptunghi datorită ambalajului, până la urmă am găsit şi o imagine cu “pătrate” cât de cât corecte. Îmi place foarte mult şi comentariul alăturat: alune² + marţipan² = lapte² (uneori e comică limba germană pentru că are un umor tare sec: autorul a dat “factor comun” cuvintele “ciocolată cu” şi apoi a împărţit egalitatea cu acestea). Constantin Titus Grigorovici

P.S.

Reprezentarea grafică a unei funcţii se face pentru a putea înţelege mai bine variaţia sa, adică “comportamentul” acesteia în general sau în anumite puncte. Cei puţini, cu o imaginaţie numerică bună, le înţeleg oricum, dar pentru a le accesibiliza cât mai multor persoane, funcţiile se reprezintă grafic. Iniţial reprezentarea grafică a funcţiilor a făcut parte din strădania de a transmite studenţilor înţelegerea pentru evoluţia fiecărui tip de funcţie în parte. De abia ulterior reprezentarea grafică a devenit un scop în sine (problemă sau exerciţiu, de dat ca temă şi apoi la testare), coborând cu timpul în liceu (nu vreau să comentez aici despre ce înţelege un elev care învaţă doar graficul funcţiei de gradul I).

Prin această postare, dar şi prin multe altele înainte, doresc să atrag în primul rând atenţia asupra faptului că Teorema lui Pitagora prezentată doar numeric este abstractă şi greu de înţeles pentru majoritatea elevilor. Doar cei obişnuiţi deja în a prelua o reţetă fără comentarii (aşa se face) o vor aplica din prima şi o vor considera uşoară. Toţi ceilalţi însă se vor duce acasă buimăciţi şi vor trebui şi ei dresaţi de către părinţi sau de către profesorii particulari înspre aplicarea reţetei. De aplicat, o vor aplica până la urmă, dar de înţeles nu o vor înţelege, matematica întărindu-şi astfel în mintea majorităţii caracterul ei de colecţie de reţete de nepătruns, în cel mai bun caz nuanţate cu un iz de hocus-pocus.

Datorită multelor insistenţe din partea mea în legătură cu figura cu pătrate în exteriorul triunghiului dreptunghic s-ar putea înţelege că am o “fixaţie”, o obsesie legată de această figură. Total greşit! Prin toate aceste reveniri şi atenţionări doresc doar să transmit că în cazul absenţei pătratelor ca figură geometrică în exteriorul triunghiului, Teorema lui Pitagora reprezintă un fenomen abstract, inaccesibil unei înţelegeri reale pentru majoritatea elevilor. Puteţi verifica desigur şi câţi adulţi nematematicieni o înţeleg în jurul dvs. Să vedeţi ce figură fac diverse persoane când le arăt Teorema lui Pitagora în baie pentru că nu înţeleg: ceea ce ţin ei minte din şcoală o reţetă de calcule într-un anumit format, iar aici eu le arăt nişte pătrate.  Vă daţi seama cum se uită când îi întreb câte pătrăţele sunt în pătratul cel mic (9), dar în pătratul mijlociu (16); dar în pătratul cel mare (aici unii trebuie să se forţeze bine până deduc 25). Unii încă nici acum nu pricep ce vreau şi trebuie să-i întreb cât face 9 cu 16: abia acum se luminează la faţă şi reuşesc să facă conexiunea între ce au învăţat în şcoală şi ce văd pe perete. Abia acum înţeleg DE CE funcţiona reţeta aia.

Mai ales în vremurile din urmă, când majoritatea covârşitoare a elevilor au crescut cu prezenţa constantă a ecranului, aceştia nu mai au puterea de imaginaţie dezvoltată astfel încât să înţeleagă ce se întâmplă în Teorema lui Pitagora (nici dacă le-o demonstrăm pe calea asemănarea triunghiurilor + teorema catetei, adică prin rapoarte, nu înţeleg mare lucru).

Aşadar, pătratele respective construite în exteriorul unui triunghi constituie de fapt “reprezentarea grafică” a Teoremei lui Pitagora. Desigur că interioarele pătratelor respective trebuie colorate, haşurate, pentru a sugera că vorbim despre suprafeţele lor. Astfel, putem constata că există două forme extreme pentru textul Teoremei lui Pitagora.

FORMA NUMERICĂ: În orice triunghi dreptunghic suma pătratelor lungimilor catetelor este egală cu pătratul lungimii ipotenuzei. În acest caz cuvântul “pătrat” se referă la operaţia de “puterea a doua”. Această prezentare a teoremei este una curat numerică, abstractă, dar uşor de reţetat pentru aplicaţii în probleme.

FORMA GEOMETRICĂ: În orice triunghi dreptunghic suma ariilor pătratelor catetelor este egală cu aria pătratului ipotenuzei. În acest caz cuvântul “pătrat” se referă la figura geometrică vizibil construită în exteriorul triunghiului pe fiecare latură. Această prezentare a teoremei este una destul de clar de înţeles pentru majoritatea elevilor, dar anevoios de aplicat pe exemple concrete (doar n-o să desenăm în fiecare problemă cele trei pătrate!, fără să mai discutăm de cazurile cu lungimi neîntregi)

Analizând cele două variante, putem spune că forma geometrică, cea cu pătrate în exterior, este una potrivită introducerii şi înţelegerii fenomenului, pe când forma numerică, cea cu “puterile a doua” una mult mai practică pentru scriere şi pentru aplicaţii ulterioare în calcularea celei de a treia laturi. O predare corectă trebuie în mod automat să le includă pe amândouă, cea geometrică pentru înţelegere la început, apoi cea numerică pentru scriere şi aplicaţii în continuare.

Pentru a nu da două variante de text diferite (cea cu “arie” respectiv cea cu “lungime”), cel mai sănătos este să dăm un text care să le cuprindă oarecum pe amândouă, un text care omite ambele cuvinte şi care totodată le subînţelege pe ambele, text care era folosit înaintea reformei din 1980 (reformă evidenţiată între altele printr-o rigurozitate excesivă):

FORMA DE COMPROMIS: În orice triunghi dreptunghic suma pătratelor catetelor este egală cu pătratul ipotenuzei. Faţă de avantajele enumerate mai sus, acest text este şi mai scurt, deci mai uşor de cuprins de către minţile elevevilor. În plus, acest text forţează atât imaginaţia, cât şi intuiţia elevilor, ambele caracteristici fiind foarte importante în viaţa ulterioară de adult.

Mai trebuie lămurit un aspect important: oare, cam de câte ori  trebuie făcută figura cu pătrate în exterior la o clasă? Eu o fac o dată pentru triunghiul (3, 4, 5), cu fiecare pătrat împărţit în pătrăţele unitare (la fel ca la exemplul cu ciocolata), şi încă o dată ora următoare cu pătratele doar haşurate (interiorul colorat), pentru generalizare. Mai departe ne concentrăm asupra formei scrise în cât mai multe exemple. După ce au văzut primul desen, la următoarele exemple de calcul elevii vor prelua prin analogie forma scrisă de rezolvare, gândindu-se că este la fel ca atunci cu ciocolata.

Să nu încheiem înainte de a arunca o privire şi pe YouTube (cuvânt de căutare: pitagora), unde găsesc mai multe preocupări faţă de subiectul nostru. În primul rând amintesc “filmuleţul” https://www.youtube.com/watch?v=vMyv5mRzzMU (ThePitiClic) în care autorul ne explică încă o dată cele de mai sus. Apoi găsim una dintre cele mai bune explicaţii, o demonstraţie cu apă: https://www.youtube.com/watch?v=CAkMUdeB06o

P.P.S. O cunoştinţă care a citit acest text înainte de publicare ne-a trimis următorul comentariu: Eu la şcoală am învăţat-o cu terenuri de tenis de mărimi diferite şi spectatori care priveau dintr-un triunghi şi mă miram de ce sunt terenurile pătrate şi de ce stau spectatorii într-un triunghi : )

În postarea precedentă am prezentat cum se găsesc numerele Fibonacci consecutive 8 şi 13 la alinierea fructelor de pe un ananas. Tot acolo am amintit în treacăt şi despre o creangă de pin pe care am găsit numerele Fibonacci consecutive 5 şi 8, aşa că m-am gândit să vă prezint şi această găselniţă personală, în caz că cineva s-ar fi putut gândi că situaţia prezentată la ananas ar fi una singulară. Şi, da, aceasta este o găselniţă personală, pe care nu am întâlnit-o niciunde în literatura studiată (unde se găsesc indicii despre conurile coniferelor, dar nu şi despre crengile acestora).

Aşadar, cum am găsit situaţia ce urmează? Simplu: făceam într-o vară un foc pentru grătarul de seară şi spărgeam nişte lemne dintr-un pin tăiat în anul precedent. Am vrut să crestez o creangă “de-a lungul”, aşa că o ţineam culcată lovind-o cu toporul pe lungime. Probabil că n-am lovit destul de tare, aşa încât a crăpat doar primul strat de lemn, cel din ultimul an de creştere, dar a rămas intact stratul interior. Când m-am uitat la acesta, am văzut nişte adâncituri perfect aliniate pe toată suprafaţa sa. În momentul acela am avut o bănuială, aşa că am pus lemnul de-o parte şi mi-am continuat activitatea de pregătit a grătarului cu alte lemne. Apoi am luat lemnul cu pricina la studiat şi iată ce am găsit.

Întrebând o colegă, am aflat că porii respectivi, frumos aliniaţi, sunt canale rezinifere (de răşină), cuprinse în zonele de lărgire a razelor medulare. Apropos, cum vă simţiţi când “dă” cineva în voi cu jargon de specialitate din afara zonei dvs. “de confort”? Cam aşa se simt şi elevii când “dăm” în ei cu jargon prea dur din specialitatea noastră. Din ce am înţeles eu, prin acei pori copacul “transpiră răşină” la nevoie.

Este evident că aici este loc de o vastă cercetare, de care însă eu nu mi-am luat timp până acum, având alte priorităţi. De pildă, pare destul de logic că la o creangă mai groasă vom găsi numere consecutive Fibonacci mai mari. Sau poate nu? Titus Sylvestris

În grupul celor mai spectaculoase şi mai cunoscute probleme de matematică sunt aglomerate de fapt mai multe “vedete”, realizarea unei ierarhii stricte între acestea fiind practic imposibilă. Totuşi, chiar dacă pentru unii s-ar putea să nu reprezinte vârful unei astfel de selecţii, problema lui Fibonacci cu iepuraşii este sigur în “top 10” al celor mai frumoase probleme din toate timpurile, şi nu fac această afirmaţie doar din punct de vedere al multitudinii de aplicaţii a şirului numerelor lui Fibonacci. Problema în sine este frumoasă, deosebit de provicatoare pentru gândirea umană în general, dar şi în particular pentru persoana (elevul) care primeşte spre rezolvare problema fără a-i cunoaşte răspunsul şi algoritmul aritmetic de generare a numerelor. Dar nu numai atât, problema reprezintă o provocare serioasă chiar şi pentru profesorul de matematică, care cunoaşte atât răspunsul (şirul lui Fibonacci) cât şi forma relativă a problemei: cum se deduce însă din problema iepuraşilor proprietatea caracteristică de generare a şirului cu pricina?

Acestor întrebări trebuie neapărat să le mai adăugăm una de ordin pedagogic: în ce clasă ar fi potrivit să propunem această problemă elevilor? Şirul lui Fibonacci apare în liceu la clasele de real în studiul şirurilor. Oare nu ar trebui să apară şi la clasele de uman? Dar problema în sine cu iepuraşi nu apare niciunde. De ce? Ce are această problemă, de profesorii nu se gândesc să o facă? Nici profesorii individual, nici organizatorii de programe, dar nici autorii de manuale (nu am o pasiune deosebită de a colectoa toate manualele ce apar, dar oricum nu am ştiinţă să existe într-un manual oficial; dacă există îmi cer scuze). Revin la intrebare: în ce clasă ar fi potrivit de făcut această problemă?

Eu nu deţin neapărat un răspuns hotărât la această întrebare, dar ştiu sigur că a lăsa elevii să plece din şcoală fără să fi cunoscut această problemă este mare păcat. Un argument în favoarea acestei afirmaţii este faptul că numerele lui Fibonacci sunt unele dintre destul de puţinele situaţii matematice care au penetrat cultura universală, prezenţa acestora în renumitul roman Codul lui da Vinci fiind doar un exemplu în acest sens.

Problema apare în cartea Liber abacci a lui  Leonardo Pissaro, zis şi Fibonacci, în a doua ediţie a acesteia din 1204. Iată o cât de cât curată variantă a problemei: Într-o curte sunt aduşi o pereche de iepuraşi pui (un băieţel şi o fetiţă). Pui de iepuri se maturizează într-o lună. După maturizare încep să facă pui, sarcina durând o lună şi fiecare naştere aduce pe lume o pereche de pui (un băieţel şi o fetiţă). Aceştia se maturizează într-o lună şi după încă o lună de sarcină au şi ei pui (întotdeauna o pereche). Adulţii aduc pe lume după fiecare lună câte o pereche de pui. Câte perechi de iepuri vor fi după un an?

Câţiva ani la rând am prezentat această problemă la clase liceale de uman, folosind farmecul deosebit exercitat chiar şi asupra ne-matematicienilor. Astfel, probelma poate fi prezentată într-o formă liberă de orice constrângere de rigurozitate scriptică a unei lecţii matematice anume. Ţinând cont că elevii de la uman nu au o deosebită capacitate de imaginaţie şi înţelegere a unor situaţii, capacitate necesară pentru găsirea numerelor şi pentru sintetizarea modelului comportamental al acestor numere, am căutat o cale cât mai atractivă de a le aduce în faţă problema.

Concret, am strâns de-a lungul anilor un sac de iepuraşi din pluş, mai mari sau mai mici, cu care fac elevilor o prezentare simulată a situaţiei descrisă în problemă (elevilor trebuie să le atragem atenţia de câteva ori că vom prezenta situaţia cu un iepuraş, gândind însă că este vorba despre o pereche (!). Astfel, încep prin a le pune pe masă un iepuraş mic (1). În pasul al doilea, adică “după o lună” înlocuiesc acest iepuraş cu unul mare (din sacul cu iepuraşi de pluş de pe masă), adică tot (1). După “încă o lună” aceştia capătă pui, deci pe lângă iepuraşul mare mai scot şi unul mic pe masă (2). După “încă o lună” noii pui se maturizează (îl înlocuiesc pe cel mic cu unul mare), iar cei iniţiali mai au o pereche de pui (scot din nou un iepuraşi mic), având pe masă doi iepuri mari şi unul mic (3). Peste “încă o lună” înlocuiesc iepuraşul mic cu unul mare şi în paralel scot din sac doi iepuraşi mici, ca reprezentanţi ai celor două perechi de pui ai celor două perechi deja adulte, având astfel pe masă trei iepuri mari şi doi mici (5). În general reuşesc să merg încă doi-trei paşi, (8) şi (13), cel mult (21), într-o cascadă de iepuraşi care tot “ies din sac”, după care mă opresc în râsetele generale ale audienţei. Iată în acest sens o “poză de grup” de la una din ultimele “reprezentaţii” ale problemei.

Las câteva momente de râs general apoi, după liniştirea atmosferei, elevii primesc sarcina să încerce pe caiete o formă de contabilizare pe paşi a numărului de iepuraşi (şi aici trebuie repetat că scriem 1 şi înţelegem o pereche de iepuri). În funcţie de timpul alocat, în final încerc întotdeauna la tablă realizarea unei scheme care să arate în ce fel evoluează numărul iepuraşilor, iar la marginea acestei scheme scriem la fiecare nivel numărul corespunzător acestei etape. Este evident că nu putem merge foarte mulţi paşi pentru că diagrama creşte puternic, aşa că destul de repede elevii trebuie să facă transferul de concentrare de la diagramă la numerele alăturate şi să “observe” modelul comportamental aritmetic după care apar acestea. În final facem un tabel separat cu 13 poziţii (start + 12 luni), în care cuprindem numerele obţinute şi îl completăm până la capăt. Iată şi o variantă de diagramă găsită pe net ca sugestie de lucru (să nu vă tot arăt variantele pusă de mine pe tablă). Spre deosebire de alte imagini ce se găsesc pe net, aceasta scoate în evidenţă atăt ideea de pereche, cât şi prin linie continuă o anumită pereche de iepuri, respectiv prin linie întreruptă naşterea unei noi perechi.

După cum am mai scris, iarna aceasta am cunoscut cartea Drăcuşorul cifrelor în care problema apare într-o formă foarte accesibilă elevilor de gimnaziu. Şi în desenele din carte sunt prezentaţi iepuraşii dublaţi (deci ca pereche) astfel încât este rezolvată şi situaţia disonantă că numerele lui Fibinacci se referă la perechile de iepuri (nu câţi iepuri, ci câte perechi). Ca semn de apreciere faţă de elevul din clasa a VII-a care mi-a împrumutat cartea înainte de vacanţă, am prezentat clasei respective această problemă în prima oră după vacanţa de iarnă (şi a mers foarte bine, deci în această formă jucăuşă funcţionează foarte bine şi la gimnaziu).

Lecţia funcţionează însă foarte bine şi la adulţi ne-matematici. La inceputul lunii decembrie am prezentat-o într-o întâlnire a Consiliului profesoral, la partea pedagogică, iar colegii (învăţătoare şi profesori de toate materiile) au reacţionat la fel de pozitiv ca şi elevii. Mai mult, o colegă mi-a dăruit înainte de vacanţă un tricou pe care desenase o grămadă de iepuraşi şi numerele lui Fibonacci. Cu mulţumirile de rigoare vă prezint şi dvs. desenul de pe acel tricou. Titus şi iepuraşii

Ideea predării probabilităţilor chiar din clasele mici gimnaziale este în sine o idee năstruşnică prin prisma următorului gând: probabilităţile sunt un fenomen matematic ce ţine exclusiv de viitor, de anticiparea viitorului, pe când gândirea copiilor este profund ancorată în prezent. Urmare a acestui aspect ar rezulta că subiectul calculării probabilităţilor nu este unul de a V-a, ci mai degrabă unul de final de a VI-a, chiar poate de a VII-a. Pe vremuri probabilităţile se studiau doar în liceu. Oricum, această lecţie este una destul de liberă, nelegată în mod special de altele, decât prin faptul că trebuie să fi fost studiate deja rapoartele şi procentele. Vreau să spun prin aceasta că lecţia nu are alte îngrădiri de ordin structural matematic, putând fi astfel poziţionată oricând (ea se face într-un anumit punct al programei doar pentru că aşa s-a convenit, nu pentru că ar fi matematic obligatoriu acolo).

Oricum, tema ar trebui abordate prin prisma gândurilor pedagogic naturale că trebuie să o luăm de jos, cât mai de jos, cu răbdare şi multe exemple, pentru a nu pierde elevi pe drum chiar de la început. Nu susţin că aşa nu pierzi elevi pe drum (cel care nu vrea să fie atent tot nu va pricepe nimic din noua temă), cum nu vreau să susţin nici că toţi elevii vor înţelege totul (lecţia va fi dusă tot de către elevii buni, cei care duc de obicei toate lecţiile). Dar măcar o astfel de abordare asigură faptul că las portiţa deschisă şi toţi elevii au ocazia să participe, pentru că aceste cunoştinţe nu presupun multe altele anterior bine dobândite. Piviţi mai întâi pozele lecţiei pe tablă:

După cum simţiţi, lecţia are un profund caracter ludic, deşi eu nu am aruncat nici măcar o dată cu un zar sau cu o monedă pe parcursul acestei ore. Toţi elevii au văzut cum este să arunci cu zarul sau cum se aruncă la începutul unui meci cu moneda pentru a se stabili terenurile fiecărei echipe. Desigur că dvs. trebuie să vă imaginaţi dialogul constant cu clasa, a cărui umbră apar cele scrise pe tablă şi în caiete. Întreaga lecţie a fost prezentată sub formă de întrebări, descoperirea acesteia, generarea lecţiei prin problematizare făcând-o foarte atractivă pentru elevi; până acolo de atractivă încât nu a mai fost nevoie de nici o definiţie, de nici o formulă de calcul a probabilităţii. La o oră ulterioară, eventual sub forma unei analize retrospective mai teoretice se poate da şi o definiţie (cazuri favorabile supra …).

Am spus că nu am aruncat cu zaruri,dar am scos din pungă acele zaruri ciudate cu 12 sau cu 20 de feţe, prezentându-le elevilor ca să ştie despre ce este vorba (dvs. le cunoaşteţi din postări mai vechi pe acest blog). Calendarul dodecaedric nu l-am avut în clasă, dar l-am descris şi elevii n-au avut nici o problemă în a răspunde cerinţelor. La aruncarea cu un calendar dodecaedric trebuie să explic întrebările, care au fost doar orale: probabilitatea să ne iasă o lună care începe cu litera i; probabilitatea să ne iasă o lună cu 31 zile; probabilitatea să ne iasă o lună care are numele de la un număr (octombrie vine de la 8); probabilitatea să ne iasă o lună care are numele de la un împărat roman (iulie de la Iulius Ceasar; august de la Augustus Ceasar).

Atrag atenţia asupra modului repetitiv “again and again” în care curg exemplele lecţiei, oferind astfel majorităţii elevilor suficient timp pentru a se acomoda cu noile cunoştiinţe, cu noua tipologie a scrierii. Doar elevii brilianţi în ale matematicii au capacitatea de a pricepe “din prima” o lecţie nouă. Ceilalţi au nevoie de multe exemple şi exerciţii până prind noua mişcare, cu toate aspectele ei, iar noi, profesorii, trebuie să pricepem acest fapt, altfel vom rămâne în continuare “o castă” de ciudaţi care chinuie copiii şi împotriva căreia se vor răscula tot mai des şi tot mai puternic părţi tot mai mari din societate.

Lecţia mai bifează un aspect important: ieşirea matematicii din zona sa internă de confort, prin apelarea atât la zarurile neobişnuite cu 12 sau 20 de feţe (am arătat că există şi cu 8 sau cu 10 feţe), cât şi prin folosirea minunatului exemplu al calendarului dodecaedric, cu scurte incursiuni în afara matematicii (nu aş merge până la folosirea termenilor de interdisciplinaritate sau transdisciplinaritate – Doamne cât ne mai plac termenii teoretici care-i dau pe spate pe cei din jur! – dar se simte totuşi un iz din acestea).

Legat de exemplul aruncării cu două zaruri, elevii trebuie ajutaţi să înţeleagă folosind două aspect. Mai întâi faptul că “să ne imaginăm că” aruncăm cu două zaruri de culori diferite (de ex. unul roşu şi unul albastru). Astfel vor înţelege că există doar un eveniment (5, 5), dar că există două evenimente cu 3 şi 4, adică (3, 4) şi (4, 3). Acest fapt este apoi “cristalizat” într-un tabel pătrat din care deducem că există 36 de cazuri teoretic posibile.

Mai rămâne de lămurit un singur aspect, cel evocat la început: de ce nu am aruncat cu zaruri? Pe lângă faptul că o oră de aruncat cu zarurile, o oră de tip “laborator de matematică”, s-ar fi lungit dincolo de limitele orei de clasă, există un aspect foarte important: prin faptul că i-am forţat pe elevi să-şi imagineze, deşi de fapt nu le-am arătat nimic, i-am forţat pe elevi să-şi folosească imaginaţia. Acest aspect este foarte important într-o lume plină de ecrane în care copiii de la vârstele cele mai fragede nu-şi mai folosesc imaginaţia pentru că primesc direct povestea prin intermediul imaginilor. Nu mai este ca pe vremuri când copilului i se spunea o poveste, iar mintiuca lui trebuia să-şi imagineze cele povestite oral, antrenându-se să-şi creeze astfel propriul său film interior. Astfel, mai ales o temă aranjată atât de atractiv, care are la bază experienţe ale elevilor din afara şcolii, trebuie neapărat folosită ca ocazie pentru antrenarea imaginaţiei.

P.S. Cu ocazia Centenarului Marii Uniri am gândit şi am scris un articol de analiză a situaţiei învăţământului matematic din România, sub gândul Unde suntem şi cum întâmpinăm Centenarul. Din păcat, ce a ieşit este destul de supărat, departe de orice atitudine festivă potrivită momentului. Riscam să obţin doar o imagine tip Cristian Tudor Popescu. Ca urmare, acest eseu a ajuns în arhivă, în aşteptarea unei forme mai pozitive de exprimare a gândurilor respective. În lipsă de altceva aţi avut ocazia să citiţi prezentarea lecţiei despre probabilităţi. C.T.G.

De-a lungul timpului oamenii au inventat diferite metode prin care să-i sprijine pe elevi în a reţine anumite informaţii considerate importante la o lecţie. În acest context se încadrează şi următoarea imagine pentru reţinerea valorilor importante ale lui sinus şi cosinus. Este evident că măsurile afişate sunt doar orientative.

Într-un context aparent asemănător, eu cunosc o altă imagine cu unghiurile dintre degetele unei mâini. Dacă deschidem cât mai larg evantaiul degetelor, până când cel mare şi cel mic devin oarecum colinear opuse, atunci vedem că obţinem trei unghiuri relativ egale şi unul dublu, cărora – prin împărţirea lui 180^o la 5 – le putem asocia măsurile 36^o de trei ori şi 72^o o dată, care sunt unghiurile ce apar în pentagramă (steaua în 5 colţuri), asociată cu tăietura de aur, implicaţiile acesteia în trupul umenesc etc. cos/sin

În toamna anului 2015 am avut postări pe tema Gândirea aritmetică vs. Gândirea algebrică, înţelegând prin acest titlu însoţirea elevului în trecerea sa din stadiul gândirii operaţionale concrete spre stadiul gândirii operaţionale formale, adică de la gândirea specifică copiilor de ciclu primar la stadiul adult de gândire. Conform lui Jean Piaget aceasta se petrece undeva în jurul vârstei de 11 ani.

Desigur că există excepţii în ambele sensuri. De pildă, la unii copii această trecere apare mai rapid, aceştia fiind pur şi simplu mai precoce. Totuşi, trebuie să fim foarte atenţi în goana noastră sau a părinţilor după cât mai mulţi “mici Einsteini”: nu ar trebui confundată orice aparentă precocitate cu situaţii în care anumiţi copii stochează informaţii de adult şi folosesc o terminologie corespunzătoare total nepotrivită vârstei, dobândită eventual chiar printr-o simplă învăţare pe de rost. Iată două exemple în cascadă: copilul care vine din grădiniţă şi ştie să numere pornind de la zero, iar apoi eventual ştie să strige şi la sfârşitul numărării: “infinit”. Urmărind de-a lungul anilor astfel de copii în dezvoltarea lor observăm că, de obicei aceste elemente de cunoaştere sunt destul de superficiale, o “spumă” de poleială aparentă, care însă cu timpul este abandonată, copilul dovedindu-se mai târziu absolut normal.

Pe de altă parte, există desigur şi copii care fac această trecere mai greu sau mai târziu, fie pentru că aşa le este felul, fie pentru că le este defectată dezvoltarea naturală din diferite motive, cum ar fi de pildă datorită folosirii diferitelor ecrane (TV, calculatoare, deşteptofoane, toate generatoare de ADHD).

Oricum, această trecere nu are loc la un copil brusc şi în nici un caz nu are loc la fel sau în acelaşi moment la toţi elevii dintr-o clasă, aşa încât o abordare cu respect faţă de fiinţa copilului ne-ar obliga să lucrăm cu multă răbdare şi tact pedagogic la subiectele care fac trecerea între cele două forme de gândire.

Subiectul principal asupra căruia am atenţionat accentuat în acest sens este introducerea operaţiei de putere din clasa a V-a, anume faptul că această temă are două etape distincte, câte una în fiecare din cele două forme de gândire: etapa de respectare a ordinii operaţiilor, corespunzătoare stadiului de gândire operaţională concretă, iar apoi etapa de încălcare a ordinii operaţiilor pe baza formulelor de operaţii cu puteri, corespunzătoare stadiului de gândire operaţională formală.

De obicei prima parte este neglijată, trecerea la a doua parte făcându-se foarte rapid, din prima oră, lăsându-i pe mare parte dintre elevi într-o totală “ceaţă” legat de această nouă operaţie. În postarea http://pentagonia.ro/gandirea-aritmetica-vs-gandirea-algebrica/ din sept. 2015 ofeream un material de bază din prima categorie de exerciţii, recomandând ca lecţia să rămână un pic în această zonă elementară înainte de a merge mai departe în zona de gândire algebrică. Prin “zonă elementară” înţelegeam atunci introducerea operaţiei de putere, înţelegerea şi fixarea acesteia (elevii să nu aibă tentaţia de a zice că 2³ = 6 etc.), cât şi înţelegerea cazurilor particulare  cu 1 şi cu 0 (1ⁿ = 1, n¹ = n, 0ⁿ = 0, dar n⁰ = 1 şi nu n⁰ = 0).

Între timp, din 2015 încoace au apărut în diferite culegeri sau manuale noi seturi cu exerciţii conţinând toate cele cinci operaţii, pur şi simplu aşa numitele “exerciţii de ordinea operaţiilor”. Stabilizarea acestui nivel se face cel mai bine pe exerciţii de calcul în care nou învăţata operaţie de putere se alătură celor patru operaţii de bază cunoscute deja din clasele primare. Ordinea operaţiilor este un subiect cunoscut, iar apariţia unui nou nivel de prioritate este foarte uşor primit de către toţi elevii, acesta trebuind doar exersat. În cadrul exerciţiilor cu toate cele cinci operaţii amestecate – cu sau fără paranteze – exersarea extinderii ordinii operaţiilor se face foarte bine alături de mai sus prezentatele cunoştinţe din zona elementară a operaţiei de putere, iar asta funcţionează foarte bine la majoritatea elevilor pentru că aceştia sunt setaţi din clasele mici să calculeze.

Acestor gânduri onorat cititorul le poate contra-argumenta cu următoarea întrebare: bine, bine, dar cu elevii buni ce facem, că se plictisesc “de moarte” la aceste “banalităţi” şi, după cum se ştie, subsolicitarea este la fel de dăunătoare ca şi suprasolicitarea. Ce facem deci cu elevii buni în acea perioadă scurtă, de cel mult o săptămână, în care îi lăsăm să exerseze puterea alături de celelalte operaţii în stadiul operaţional concret? Un răspuns posibil vine de la următoarea “problemă” asupra căreia ne atrage atenţia profesorul Vasile Bobanciu în lucrarea sa Caleidoscop matematic, Editura Niculescu, ed. a III-a, 2005, la pagina 71 (cu răspunsuri la pagina 100).

Astfel, aflăm că în anul 1907 profesorul Ion Ionescu a propus cititorilor Gazetei Matematice să scrie un miliard utilizând toate cele zece cifre o singură dată. În lunile următoare s-au primit mai multe soluţii, ce au fost prezentate în anul 1908 în Gazeta Matematică. Preluând ideea, eu le propun elevilor de clasa a V-a doar să le verifice pe rând pe fiecare dintre aceste scrieri, adică să observe dacă sunt scrise într-adevăr cu fiecare cifră folosită măcar o dată şi doar o singură dată, iar apoi să calculeze dacă acestea dau rezultatul 1.000.000.000:

(2 + 3 + 4 + 7 + 9) ∙ 5 ∙ 8 ∙ 10⁶

(897 + 106 + 4 – 2 – 5)³

2^{3 ∙ 6 –  9} ∙ 5^{8 + 7 + 4 – 10}

2³ ∙ 4 ∙ 5^{9 + 6 – 7} ∙ 8 ∙ 10

2⁹ ∙ (8 + 7 – 10)^{63 – 54}

2⁶ ∙ 5⁷ ∙ [8 ∙ (1 + 9) + 4 ∙ 30]

5 ∙ 20 ∙ (1 + 3 ∙ 9 – 4 – 6 – 8)⁷

(897 + 106 + 5 – 2 ∙ 4)³

(64 – 59)⁸ ∙ 20 ∙ (3 – 1)⁷

(510 + 4 – 2) ∙ (73 – 68)⁹

[2 ∙ 10 ∙ (4 ∙ 5 + 6 + 7 + 8 + 9)]³

(40 : 8 – 3)^{(62 + 1) : 7} ∙ 5⁹

Unele sunt mai uşoare, altele mai grele (pentru elevul mediu în sem. I din clasa a V-a); la unele dintre acestea anumiţi elevi reuşesc să găsească singuri faptul că zero-urile de la sfârşit sunt generate de produse de 2 ∙ 5, situaţii de genul 2⁶ ∙ 5⁷ generând din start şase zero-uri la sfârşitul rezultatului. Pe de altă parte, în acestea apar şi situaţii de tipul 10³ ∙ 10⁶ = 10⁹ pentru obţinerea unui miliard. În acest sens, respectivele exerciţii devin o bază bună pentru predarea prin problematizare în vederea “descoperirii” formulelor de operaţii cu puteri (în orele următoare). Anexez o variantă pdf a acestor exerciţii. CTG

Rezult 1000 000 000.pdf

La peste un sfert de secol după schimbările din 1990 în şcolile din România se folosesc încă instrumentele de tip vechi. Nu vreau să susţin că acestea sunt depăşite; şi eu le cer elevilor în clasa a VI-a cunoscutele truse chinezeşti în cutiuţă de metal care îi ajută să înţeleagă toate mişcările specifice. Din clasa a VII-a le cer însă achiziţionarea unui alt instrument. Despre ce este vorba?

În vestul Europei se foloseşte de mult timp un instrument din plastic transparent care poate face orice construcţie în afara de trasarea cercurilor. Acesta este cunoscut sub denumirea de echer geometric: Geo-dreieck în germană pe scurt (complet ar fi Geometrie-Dreieck), Equerre géometrique pe franceză, Geometrical square pe engleză, Escuadra geometrica pe spaniolă, Triangolo Geometrico pe italiană etc. Iată o imagine cu acesta:

Haideţi să-l analizăm pas cu pas în elementele sale. În primul rând ne uităm la sistemul de linii paralele (paralele cu ipotenuza echerului), din 5 în 5 mm depărtate de ipotenuză. Cu acestea poţi trasa paralele la o dreaptă. Dacă punctul prin care doreşti să trasezi paralela nu este la distanţă de 5, 10, 15 etc. cm, atunci te poţi ajuta de cele două gradaţii suplimentare în mm cu care poţi poziţiona ipotenuza paralel faţă de dreapta iniţială.

Al doilea element important este linia mediană a acestui echer (îmi place să numesc astfel înălţimea din unghiul drept pe ipotenuza echerului, totodată şi mediană, bisectoare, mediatoare şi axă de simetrie a instrumentului). Cu ajutorul acesteia în primul rând se pot trasa perpendiculare pe o dreaptă dată, perpendiculare care să traverseze dreapta. O astfel de perpendiculară este mult mai bună pentru că poate trece dintr-o parte în cealaltă a dreptei iniţiale “dintr-o mişcare”, fără mutarea echerului şi fără acea “rotunjire” deranjantă la piciorul perpendicularei, ce apare “vrei-nu vrei” la echerele de modă veche (dacă vrei perpendiculară doar pe o parte, te opreşti la dreaptă). Este atât de comodă trasarea perpendicularelor cu această linie mediană, încât cine s-a obişnuit să o folosească nu va mai accepta să lucreze cu alte echere.

Probabil că aşteptaţi să vorbesc şi de raportor, elementul cel mai vizibil, dar nu, al treilea element valoros la echerul geometric îl reprezintă gradaţia liniarului de pe ipotenuză, avându-l pe zero la mijloc, numerele crescând în ambele părţi. Cu ajutorul acesteia se poate în primul rând găsi mijlocul unui segment, fără a-l măsura şi a împărţi lungimea la doi. Pur şi simplu trebuie să poziţionezi liniarul gradat de pe ipotenuză pe segment cu capetele acestuia egal depărtate de mijlocul zero, punct pe care îl însemnăm ca mijloc.

Combinând linia mediană cu gradaţia liniarului putem foarte uşor să construim bisectoarea unui unghi. Pentru asta trebuie să poziţionăm echerul geometric cu linia mediană trecând prin vârful unghiului şi laturile unghiului tăind gradaţia liniarului de pe ipotenuză în două puncte simetrice faţă de zero, în mod similar cum am procedat la mijlocul unui segment. Practic, astfel aranjate laturile unghiului şi cu liniarul gradat în cm cuprind între ele un triunghi isoscel, linia mediană a echerului ca înălţime devenind automat şi bisectoare.

Vine în sfârşit şi raportorul la rând de a fi analizat. Acesta nu aduce numic nou faţă de ce ştie toată lumea, dar trebuie folosit cu atenţie pentru că baza sa este chiar ipotenuza echerului şi nu o linie trasată pe suprafaţa interioară a plasticul echerului (vedeţi că pe echer nu sunt scrise valorile de 0^o respectiv 180^o, linia unghiului alungit 0^o-0-180^o fiind chiar liniarul gradat în cm al echerului, punctul 0 fiind vârful acestui unghi alungit). În mod similar cu construcţia unghiurilor drepte, aceste echere geometrice au şi nişte linii ajutătoare pentru construcţia unui unghi de 45^o. În plus, având suprapunerea dintre centrul raportorului şi originea gradaţiei de pe liniar se pot trasa foarte uşor segmente de o anumită lungime la o anumită înclinaţie faţă de un segment dat (tocmai am descris construcţia triunghiurilor în cazul LUL).

Folosind linia mediană şi gradaţia ciudată a liniarului, putem construi foarte uşor şi simetricul unui punct sau al unei întregi figuri faţă de o dreaptă (privită ca axă de simetrie). Ştiu că astfel de sarcini nu sunt în repertoriul orelor de geometrie din România, dar am ţinut să prezint şi acest aspect deosebit de folositor în practică.

Vedeţi deci cât este de folositor acest instrument, permiţând construcţii foarte exacte atât pe foaia de matematică cu pătrăţele, dar în poziţii înclinate, cât şi pe coală velină (folosită la examenul de la finalul clasei a VIII-a sau la BAC). Să vedeţi ce uşor desenezi cu echerul geometric clasica figură din teorema lui Pitagora (cea cu pătratele construite pe fiecare latură a triunghiului dreptunghic)! Dar să luăm şi un exemplu mai simplu: construiţi cu echerul geometric un triunghi dreptunghic cu ipotenuza orizontală şi unghiul drept în vârf. La fel de folositor este echerul geometric şi la trasarea sistemului de axe ortogonale cu unităţi pe cele două axe ale sale, pentru trasarea punctelor şi a graficelor funcţiilor (desigur, pe foaie velină, când nu ai reperele pre-trasate ale pătrăţelelor de pe foaia caietului tradiţional de matematică). Da, echerul geometric construieşte aproape orice; doar cercuri nu ştie trasa.

Unde se găsesc astfel de instrumente valoroase? Am mai spus, sincere mulţumiri magazinelor Lidl care au tăria de a aduce măcar în fiecare septembrie astfel de echere în truse deosebit de ieftine (un echer geometric mic, unul mare şi un liniar ordinar) la 4 lei. Şi alte magazine aduc, dar neconstant şi de obicei la preţuri mult mai piperate, şi asta doar pentru că nu există o cerere constantă şi în cantităţi mari. De ce nu există această cerere? Pentru că şi după un sfert de secol de la “eliberarea oficială de comunism” organizatorii programelor şi a manualelor de matematică româneşti nu au preluat acest echer, ne-existând o recomandare oficială pentru folosirea sa.

În acest sens am o scurtă, dar edificatoare povestioară: prin 1992 m-am adresat conducerii întreprinderii Napochim din Cluj, care pe lângă lighiane şi alte castroane, producea şi instrumente geometrice din plastic transparent, cerându-le să introducă în producţie şi astfel de echere. Mi-au răspuns sec că, fie rezolv ca înainte să fie introduse prin materia din manuale, fie să plătesc eu realizarea matriţei. Am întrebat cât costă matriţa şi răspunsul “m-a dat pe spate”: era vorba de salariul meu de începător pe mai mult de un an. Q.E.D. La castroane şi lighiane aveau garanţia că se vând, la aceste instrumente deştepte aveau mari dubii. Şi uite-aşa au dispărut încet toate capacităţile de producţie româneşti, refuzând progresul.

Desigur că există echere geometrice şi mari, pentru uzul profesorilor la tablă (tot din import, e clar). Nu sunt ieftine, dar merită şi profesorul un instrument bun (iar şcolile la ora actuală chiar îşi pot permite astfel de achiziţii).

Închei această prezentare cu o precizare: imaginile de mai sus sunt toate culese de pe internet. Dacă daţi cuvinte de căutare denumirea echerului geometric în diferite limbi străine vă vor apărea şi filmuleţe postate în care puteţi vedea cum se foloseşte acesta. Dau un singur exemplu, anume un filmuleţ cu paşii de urmat pentru trasarea mediatoarei (în germană Mittelsenkrechte).

Mittelsenkrechte und Winkelhalbierende

Este interesant că autorul trasează mediatoarea cu echerul geometric, dar la bisectoare (în germană Winkelhalbierende) foloseşte metoda antică cu compasul, dovedind astfel o ciudată inconsecvenţă. Eu personal îi învăţ pe elevi în clasa a VI-a metodele tradiţionale cu rigla negradată şi compasul, iar din clasa a VII-a metodele mai moderne şi mai rapide cu echerul geometric.

Căutaţi şi cumpăraţi un astfel de echer, folosiţi-l şi veţi vedea că merită. Noi îl folosim de prin ’93-’94 şi elevii noştri a avut de atunci întotdeauna cele mai frumoase desene la examene.  Titus G.

De curând am primit o întrebare deosebit de clară despre acest subiect, întrebare la care m-am străduit din răsputeri să răspund cât mai dataliat cu putinţă. Reiau întrebarea: Dacă introducem noţiunea de unghi mai întâi în forma unghiului la centru, ar fi de preferat să definim notiunea de grad întâi pentru arce de cerc şi să definim măsura unui unghi ca măsura arcului cuprins între laturi prin deschiderea unghiului, justificând astfel şi folosirea raportorului (studiind oarecum în paralel cercul şi unghiurile, cum am văzut în Manualul de a VI-a din ’69 de Rusu şi Hollinger)? (comentariu din 22.aug. 2018 la postarea din 1.mai 2018)

Pe când făceam corectura finală şi ultimele retuşuri la eseul cu pricina, am reuşit să găsesc şi manualul de geometrie de a VI-a despre care vorbea colegul Alex D. Mai exact, am găsit două manuale ale profesorului A. Hollinger, unul din 1966 (bănuiesc că acesta este de forma celui despre care era vorba în întrebare) şi încă unul din 1977. Avem foarte multe manuale vechi acasă şi nu apuc să le studiez în detaliu; nici pe acestea nu le ştiu pe de rost, aşa că le-am luat la “puricat” în contextul de faţă. Permiteţi-mi să vă prezint ce am găsit în cele două manuale legat de subiectul discutat în prima parte a eseului ca răspuns la întrebarea de mai sus. (observaţie de pronunţie: numele se citeşte “Holingăr”)

1) Haideţi să vedem în primul rând cum erau prezentate lucrurile în manualul lui  Hollinger din 1966 (mulţumesc pentru acest manual fostei mele colege Cristian Marina, profesoară de engleză, dar mare iubitoare de matematică, care şi-a păstrat manualele din gimnaziu de pe vremuri). Iată începutul cuprinsului: Cap.I: Noţiuni introductive; Cap. II: Linia dreaptă; Cap. III: Cercul; Cap. IV: Unghiuri etc.

Să spicuim câteva aspecte din capitolul de introducere a cercului. Acesta este împărţit în nişte subteme pe care le enumăr în continuare: 29. Ce este cercul. 30. Proprietăţi ale cercului. 31. Rază, diametru, coardă, arc. 32. Mijloace practice de a obţine un cerc. 33. Aplicaţii ale cercului (aplicaţii practice ale proprietăţilor cercului în lumea înconjurătoare). 34. Mişcarea de rotaţie. 35. Cercuri egale. 36. Compararea arcelor. 37. Operaţii cu arce. 38. Măsurarea arcelor. 39. Observare. (o observaţie scrisă cu litere mai mici şi în care se spune că măsura în grade a unui arc nu indică lungimea acelui arc etc.) 40. Arce şi coarde. 41. Construcţia unui arc egal cu un arc dat. Reiau câteva pasaje din acest capitol:

34: Mişcarea de rotaţie. Când o figură plană se mişcă în planul ei astfel ca unul dintre punctele ei să rămână pe loc, se spune că are o mişcare de rotaţie. În figura 71 se arată cum putem da unei foi de hîrtie  o mişcare de rotaţie. (Foaia de hîrtie este fixată pe masă cu ajutorul unui ac.) Când o figură plană are o mişcare de rotaţie, toate punctele ei descriu cercuri sau arce de cerc, care au acelaşi centru (punctul unde este înfipt acul). Acest punct se numeşte centru de rotaţie. Cînd o roată se învîrteşte (nu cînd se rostogoleşte), ea are o mişcare de rotaţie, centrul de rotaţie fiind chiar centrul roţii.

38: Măsurarea arcelor. Ca unitate de măsură pentru arce se ia a 360-a parte din cerc, numită grad (^o). Gradul se subîmparte în 60 de părţi egale (…) Arcele se măsoară cu ajutorul unui instrument numit raportor (…)

Să ne uităm în mod similar şi la capitolul de introducere a unghiurilor. Acesta este împărţit în următoarele teme: 42. Ce este un unghi. 43. Unghi cu laturile în prelungire. 44. Compararea unghiurilor. 45. Operaţii cu unghiuri. 46 Observare. 47. Unghi la centru. 48. Unghiuri şi arce. Aici apare un titlu mai mare, Măsurarea unghiurilor, care are următoarele teme: 53. Măsura unui unghi. 54. Raportorul. 55. Observări. 56. Măsurarea unghiurilor pe teren. (…) Capitolul se încheie cu tema 72. Unghiuri mai mari ca 180^o. Reiau şi aici câteva pasaje:

42: Ce este un unghi. (…) Un unghi este format din două semidrepte care pornesc din acelaşi punct. El poate lua naştere prin rotaţia unei semidrepte în jurul capătului ei. (…) Când este vorba de mărimea unui unghi, avem în vedere porţiunea din plan cuprinsă între laturile sale (haşurată în figura 85 – un unghi ascuţit şi unul obtuz cu interiorul haşurat) sau cât de mult trebuie să rotim una din laturi ca să o suprapunem cu cealaltă (…). Laturile unui unghi sînt semidrepte (nu segmente), ele indică două direcţii. Faptul că ele sînt mai lungi sau mai scurte (desenate evident) nu influenţează mărimea unghiului. Se are în vedere deschiderea lor. Uneori este mai bine să reprezentăm un unghi printr-o bucată de carton ca în figurile 87-90. (…)

46: Observare. Compararea unghiurilor, precum şi operaţiile cu unghiuri se pot înţelege şi dacă privim unghiul ca fiind născut prin rotaţia unei semidrepte. Astfel, în figura 87, a, unghiul al doilea este mai mic decît primul; aceasta înseamnă că, pentru a aduce o semidreaptă din poziţia OA în poziţia ON, trebuie s-o rotim mai puţin decît pentru a o aduce în poziţia OB; în figura 87, b, trebuie s-o rotim tot atît, iar în figura 87, c, – mai mult. În figura 88, unghiul AON este suma unghiurilor 1 şi 2; aceasta înseamnă că, pentru a aduce semidreapta OA în poziţia ON, trebuie să o supunem unei rotaţii date de unghiul 1 şi încă unei rotaţii, în continuare, dată de unghiul 2. A roti în continuare corespunde operaţiei de adunare a unghiurilor, aşa cum după ce am dus un segment de dreaptă AB, dacă mişcăm creionul în continuare pînă în C, adăugăm segmentul BC (fig. 92). (…) Mă bazez în redarea citatelor că onorat cititorul reuşeşte să-şi imagineze figurile la care Hollinger face referire (am preferat să nu mai încarc postarea cu diferite imagini; cine ţine neapărat să vadă acele imagini şi atmosfera emanate de acestea merită să facă efortul de a vâna aceste manuale în anticariate virtuale şi a le achiziţiona; ce frumos şi sugestiv este acest cuvânt: anticariat).

47: Unghi la centru. Nu reiau din această parte decât ultimul aliniat, urmare a unei figuri ce reprezintă un ceas tradiţional, la care oarecum acele sale sunt prelungite în două semidrepte, ca laturile unui unghi: Acele unui ceas formează un unghi la centru (fig. 94).

53: Măsura unui unghi. Dată fiind legătura dintre un unghi la centru şi arcul cuprins între laturile sale, putem măsura unghiurile măsurînd arcele lor. (…)

55: Observări. Cînd măsurăm un unghi cu raportorul, noi măsurăm de fapt un arc. Cînd aşezăm raportorul peste unghi ca în figura 100, unghiul devine unghi la centru, iar arcul corespunzător este partea din marginea raportorului cuprinsă între laturile unghiului. (…)

Nu are legătură cu subiectul nostru, dar nu mă pot abţine să nu vă redau şi aliniatul 3 de la aceste observări: Un unghi şi un arc sînt lucruri cu totul diferite. Un unghi nu poate fi egal cu un arc, nici mai mare ca el, nici mai mic, aşa cum un metru nu este egal cu un kilogram, nici mai mic, nici mai mare. Ne putem imagina situaţia acestui profesor emerit, de câte ori s-o fi lovit dânsul de întrebări în ceaţă de genul: Vreţi să spuneţi că unghiul şi arcul de cerc sînt acelaşi lucru? De vreme ce se măsoară ambele în grade?

72: Unghiuri mai mari ca 180^o. Cînd o semidreaptă se roteşte în jurul unui punct, ea poate descrie unghiuri oricît de mari. Să luăm, de exemplu, acul mare (minutarul) al unui ceasornic (fig. 121). Într-o junătate de oră, el descrie un unghi de 180^o, în ¾ de oră un unghi de 270^o, într-o oră de 360^o, în două ore de 720^o ş.a.m.d. În acest manual vom folosi însă numai unghiuri mai mici decît 180^o.

Mă opresc aici cu citatele din manualul de clasa a VI-a din 1966, sperând că aţi prins linia în care preda profesorul A. Hollinger aceste aspecte. Este evidentă forma în care eu m-am format şi din care peste ani a ieşit forma de predare ce v-am prezentat-o în prima parte. Pasajele citate de mai sus le-am citit însă conştient, ca dascăl, doar acum, odată cu redactarea acestui eseu, mai exact după ce tot restul eseului a fost redactat.

*

2) În cei 11 ani trecuţi până la următorul manual, cel din 1977, s-au produs unele modificări, dar multe lucruri au rămas la fel (am vaga imagine în minte că prin 1972 a fost o scurtă reformă). Vedem ca urmare două variante aparent diferite, dar care au clar elemente comune.

Iată începutul cuprinsului manualului din care am învăţat generaţia noastră: Cap.I. Recapitulare şi completări. Cap.II. Linia dreaptă. Cap. III. Unghiuri. Rotaţia. Simetria faţă de un centru. Restul cuprinsului nu este de interes pentru subiectul de faţă. Oricum, se vede că a dispărut capitolul despre cerc. Să analizăm cum funcţionau aspectele în discuţie în acel capitol III despre unghiuri.

3.1. Noţiunea de unghi. 1. În clasele anterioare s-a arătat ce este un unghi; în cele ce urmează vom preciza această noţiune. (puţin neinspirată – pentru noi – această exprimare “vom preciza această noţiune”, dar trebuie să avem înţelegere: Hollinger avea deja o vârstă avansată, era numit profesor emerit, venea din alte vremuri; Apropos manuale vechi, noi avem un manual semnat de dânsul din perioada interbelică). Două semidrepte OA şi OB (fig. III.1) care au aceeaşi origine împart punctele din plan nesituate pe nici una din ele în două părţi. În figură una din aceste părţi este haşurată şi cealaltă este acoperită cu puncte. Cele două semidrepte împreună cu una din aceste părţi ele planului formează un unghi.

Aşadar, Hollinger dă din startul capitolului drepturi egale unghiurilor proprii (cum le numim noi acum) şi unghiurilor supraobtuze. În figura respectivă este haşurată zona care actualmente se numeşte exteriorul şi este punctată zona care se numeşte actualmente interiorul unghiului propriu. Urmează o Definiţie. Un unghi este format din două semidrepte care au aceeaşi origine împreună cu una din părţile planului determinate de ele. (UAU!!!) Apoi vin componentele unghiului: Cele două semidrepte se numesc laturile sau braţele unghiului, originea lor comună se numeşte vîrful unghiului, şi partea din plan se numeşte interiorul unghiului. (Care parte din plan? Păi, aia care am ales-o, şi am haşurat-o în această fază incipientă.)

În general, una dintre părţile planului determinate de cele două semidrepte este mai mică (cea acoperită cu puncte în fig. III.1). Un astfel de unghi se numeşte unghi convex (în subsolul paginii apare şi un comentariu: Căci, dacă M şi N sînt două puncte oarecare din interiorul lui, tot segmentul MN se află în interiorul lui – ceea ce nu mai este adevărat în cazul unui unghi neconvex). Pentru a reprezenta un unghi, se desenează numai cele două semidrepte (fără haşuri). Ca să se ştie despre care din cel două unghiuri este vorba, se face în interiorul lui un arc de cerc cu centrul în vîrful unghiului sau un alt semn. În figura III.1, unghiul convex este indicat prin două arce, şi celălalt printr-un singur arc. Când nu există nici un arc, se înţelege că este vorba de unghiul convex. (…)

2. Un unghi poate lua naştere prin rotirea unei semidrepte. De exemplu, unghiul din figura III.4 poate lua naştere prin rotirea unei semidrepte din poziţia OM pînă în poziţia ON în sensul indicat de săgeata 1 sau din poziţia ON pînă în poziţia OM în sensul indicat de săgeata 2. În ambele cazuri, semidreapta descrie (mătură) tot interiorul unghiului – ca limba unui ceas (privită ca semidreaptă). (…)

3.2. Măsura unui unghi. 1. Unghi la centru. Când o semidreaptă se roteşteîn jurul originii sale descriind un unghi AOB (fig. III.7), în fiecare dintre punctele ei descrie un arc de cerc. Punctul M  descrie arcul 1, punctul N descrie arcul 2 ş.a.m.d. (M şi N sunt situate în figură pe latura OA a unghiului AOB, şi mai este încă un arc, cele trei arce trecând dincolo de latura OB) Toate aceste arce au acelaşi centru O. Prin trasarea unuia dintre aceste arce, unghiul devine unghi la centru. Un unghi la centru este un unghi al cărui vîrf se află în centrul unui cerc. Limbile unui ceas (privite ca semidrepte) formează un unghi la centru (fig. III.8). Între un unghi la centru şi arcul său există o legătură strînsă.

Urmează, sub titlul 2. Unghiuri şi arce o scurtă prezentare a acestei legături, după care vine partea 3. Măsura unui arc pe care o cunoaştem din manualul din 1966. La fel, cunoaştem şi partea 5. Măsura unui unghi etc. Aşadar, Hollinger introduce măsura în grade mai întîi tot pe arce de cerc, iar apoi la unghiuri, chiar dacă aparent a introdus mai întâi unghiurile.

Acestea erau părerile şi punctele de vedere ale profesorului A. Hollinger în anii ’60-‘70. Părerile mele, atât cele pro, cât şi cel contra, le-am prezentat detaliat în prima parte a eseului. Înainte de a încheia îmi permit totuşi să ordonez într-un scurt rezumat ideile despre cum ar trebui să arate introducerea noţiunii de grad în primele clase gimnaziale. Cu această ocazie voi mai face şi câteva ultime observaţii metodice legate de acest subiect, în contextul ultimei programe pentru gimnaziu. Mulţumesc încă o dată pentru oportunitatea oferită de a trata această temă de detaliu atât de fină şi totuşi atât de controversată.

*

Cerinţa introducerii pe principii intuitive a noţiunilor la clasele gimnaziale mici era considerată de la sine înţeleasă înainte de reforma uitată din 1980, dar este precizată şi în noua programă. În vederea introducerii pe baze intuitive a noţiunii de grad la copii trebuie să pornim de la realitatea lumii înconjurătoare. Or, lumea înconjurătoare, din punct de vedere al copilului, este o lume în mişcare. Copilul sănătos se mişcă mult; el cu greu stă locului (poate doar dacă este ţintuit în faţa micului ecran, vrăjit de imaginile fâlfâitoare). Prezentându-i lucrurile în mişcare le înţelege cel mai bine. Acesta este unul din principiile ce mi-au fost prezentate de mult despre predarea matematicii în general şi a geometriei în particular, de către cei mai vechi decât mine în pedagogia Waldorf. Dar predarea în mişcare nu este un principiu ce ţine neapărat de această pedagogie, ci este pur şi simplu un principiu al predării sănătoase, oblogatoriu mai ales la vârstele mici. Şi se vede din plin cum Hollinger foloseşte acest principiu al predării prin mişcare la introducerea noţiunilor la clasa a VI-a (semidreapta care în rotirea sa în jurul punctului de origine “mătură” interiorul unghiului, sau punctul care rotindu-se în jurul centrului descrie un arc de cerc etc.).

Am două observaţii speciale aici, legate de poziţionarea acestui tip de predare mai ales în conexiune cu vârsta elevilor: pe vremea acestor manuale elevii mergeau la şcoală, în clasa I, după împlinirea vârstei de 6 ani. Actualmente, elevii (vorbesc de cei ajunşi anul acesta în clasa a VI-a) au mers la şcoală, în clasa pregătitoare, tot cam după împlinirea vârstei de 6 ani. Astfel, vârsta de atunci de clasa a VI-a cam echivalează cu vârsta medie a copiilor de clasa a V-a, poate cu o mică întârziere datorată celor care au fost înscrişi în clasa pregătitoare înaintea împlinirii vârstei de 6 ani. Cu alte cuvinte, semestrul II din clasa a V-a este numai potrivit pentru a introduce noţiunea de grad în mişcare, într-o formă cum am văzut-o la Hollinger (pentru cei care pot să înţeleagă şi să creadă într-aşa o predare în mişcare, detaşându-se de predarea statică din ultimii 35 de ani). Totuşi, introducerea unei noţiuni noi în mişcare nu estestrict legată de vârstele mici, ci este doar strict necesară majorităţii elevilor din clasele mici. Să presupunem că am dori să-i explicăm această lecţie unui adult care nu a învăţat-o, nu o ştie, habar nu are ce-i acela un unghi. Şi la acesta tot prin mişcare şi prin analogie cu lumea înconjurătoare o vom face cel mai eficient. Metoda statică constructivistă, pe baza unor definiţii, este potrivită doar în cazul predării prin sistematizare a cunoştiinţelor la nouă reluare (predare în spirală la cunoştiinţe anterior dobândite)

Să reluăm firul discuţiei. Aşadar, există două mişcări de bază, mişcarea rectilinie şi mişcarea de rotaţie. Pentru a măsura mişcarea rectilinie avem unităţile de lungime. Trebuie introdusă o unitate de măsură pentru rotaţie, care este o mişcare de cu totul alt tip, cauză pentru care suntem puşi în faţa unor probleme de cu totul alt tip. Unităţile de lungime măsoară mărimea unui segment, segmentul obţinându-se punând vârful unui creion pe hârtie şi mişcându-l de-a lungul unei drepte, de-a lungul unui liniar. Trebuie însă să rezistăm tentaţiei de a face exact acelaşi lucru în cazul rotaţiei. Rotind un punct, manifestat prin vârful creionului de la compas, în jurul unui centru de rotaţie – vârful acului – vom obţine un arc de cerc la care putem fi uşor tentaţi să-i măsurăm ca mărime tot lungimea. Dar acest fapt trebuie evitat cu abilitate.

Aceasta este marea provocare la introducerea unităţii de măsură pentru rotaţie, de a distrage atenţia elevului, natural manifestată către un soi de lungime, doar că rotundă, şi a îndrepta atenţia spre centrul de rotaţie. Vom face aceasta ataşându-i centrului de rotaţie o direcţie, văzând apoi cum se roteşte direcţia în jurul centrului; un fel de punct care se uită într-o direcţie şi care învârtindu-se mătură cu privirea o porţiune din planul înconjurător. Hollinger făcea asta rotind o semidreaptă cu originea chiar în centrul de rotaţie, în jurul acestui centru. Pentru a coborî din zona abstractă în lumea înconjurătoare a elevilor, obţinând astfel o accesibilizare a spuselor sale, Hollinger apela apoi la exemplul ceasurilor (desigur cu ace, cele cu afişaj digital apăreau primele spre finele anilor ’70).

Eu prefer o altă variantă: stau drept în faţa clasei, cu faţa îndreptată către uşă şi o mână ridicată orizontal în faţă. Apoi, în timp ce explic, încep să mă rotesc, arătându-le elevilor o rotaţie completă, adică până sunt iarăşi poziţionat cu faţa şi cu mâna către uşă. În acest moment le explic că o rotaţie completă se împarte în 360 de părţi numite grade. Repet oarecum mişcarea sub formă de întrebare: cât m-am rotit dacă am făcut doar o jumătate de tură şi m-am întors doar pănă la a arăta spre geam? 180^o, strigă toată clasa, apoi mă rotesc doar un sfert de tură etc. Îmediat apoi trec la tablă şi îi întreb pe elevi: dacă aş fi făcut treaba asta cu o cretă în mână pe o suprafaţă, ce aş fi obţinut? Un cerc, strigă toţi copiii. Aşa că desenăm un cerc ca manifestare a rotaţiei, şi în acesta trasez apoi diferite raze ca reprezentare a mâinii mele întinse în faţă, şi reprezint grafic astfel ceea ce am arătat mai înainte când mă roteam şi prezentam oral apariţia gradelor de rotaţie. Pe desen voi scrie 90^o, 180^o, 270^o şi 360^o atât pe cerc, cât şi pe nişte arce mici orientate cu săgeată până la direcţia respectivă. Apoi, cu o cretă colorată voi desena poziţia iniţială a semidreptei şi una finală oarecare, haşurând porţiunea măturată de semidreapta în rotire, explicând că acesta este un unghi. Aici luăm raportorul, îl poziţionăm cu atenţie exact în centrul cercului şi cu linia de 0^o pe raza iniţială şi toată lumea citeşte câte grade s-a rotit raza respectivă. Apoi scriem măsura obţinută atât pe cerc, cât şi pe o săgeată rotundă în interiorul unghiului. Astfel, măsurarea rotaţiei este transferată simultan şi la unghiuri şi la arce (cei doi “copii” ai rotaţiei).

Pe caiet însă, nu vom scrie nici o definiţie, nici pentru arc de cerc, nici pentru unghi, şi desigur nici pentru grad. Dimpotrivă, trecem repede la raportorului ca instrument de măsurare a gradelor, pentru a face repede un nou desen, anume împărţirea cercului în cinci părţi egale (aplicaţie cu caracter ludico practic) şi a stelei în cinci colţuri (pentagrama): câte grade are o parte?, iar elevii care stăpânesc bine împărţirea strigă 72^o! Ca temă se poate da desenarea unei octograme, o stea în opt colţuri, pe baza împărţirii cercului în opt părţi egale de făcut cu raportorul. Ora următoare se poate face o reactualizare prin împărţirea cercului în 9 părţi egale şi ca temă în 10 părţi egale (merge şi ca temă din prima, dar eu prefer să o fac ora următoare pentru a “aduna” şi ultimele “oiţe rătăcite”). Anexez în acest sens poza unui desen făcut zilele acestea pe post de recapitulare la începutul clasei a VI-a (avem 4 elevi noi în clasă pe care trebuie să-i iniţiem repede în aceste tehnici), ca să înţelegeţi la ce mă refer când vorbesc de desene frumoase şi abordare iniţial ludică a cunoaşterii elementelor geometrice (un desen asemănător cu roza vânturilor, dar cu 5 + 5 vârfuri, plecând de la împărţirea cercului în 10 părţi egale cu ajutorul raportorului: 360^o : 10 = 36^o etc.). Noi folosim nişte caiete fără poze pe copertă, cu foaie velină, şi câţiva elevi vor desena acest desen ca imagine pe caietul de geometrie.

În final doresc să accentuez câteva aspecte atinse pe parcurs, inclusiv prin citatele din Hollinger, dar nediscutate clar ca atare. În primul rând, consider dăunător să facem un transfer simplu de conţinut din forma de predare ce o aveam când unghiurile se introduceau doar în clasa a VI-a, un transfer ad literam în semestrul II din clasa a V-a, doar pentru că au apărut aici aceste titluri. Mult mai sănătos este ca în clasa a V-a să introduc noţiunile în mod ludic, pe baze intuitive, şi apoi, doar în clasa a VI-a, la o reluare şi stabilizare a noţiunilor, să le dăm eventual definiţii mai ordonate ale noţiunilor. Acolo nu mai este nevoie să vorbim despre rotaţie şi putem da direct gradele ca unităţi de măsură a unghiurilor (în vremurile noastre acestea au întâietate în faţa arcelor). Recitiţi vă rog, în acest sens, prima frază de la Noţiunea de unghi din manualul din 1977.

În altă ordine de idei, doresc să accentuez, şi rog cititorul a se întoarce cu atenţie la citatele de mai sus din manualele lui Hollinger: dânsul lăsa o perioadă bună de la introducerea unghiului până când apărea măsura unghiului (la fel şi la arce). Pe parcursul acelor lecţii dânsul vorbea doar de mărimea unghiurilor, le compara, le aduna etc., nu măsurile (adică nişte numere), ci unghiurile ca obiecte în sine. Recitiţi vă rog temele 36-38 de la componenţa capotolului despre cerc şi temele 44-54 din cadrul capitolului despre unghi în manualul din 1966.

Închei revenind în prezent, anume cu câteva citate din noua programă de matematică, pasaje care subliniază cât de mult se revine prin aceasta la stilul de predare de pe vremea profesorului Abraham Hollinger: Note definitorii (…) O caracteristică a acestei programe este că, în clasele a V-a şi a VI-a, noţiunile sunt prezentate intuitiv, evitându-se abuzul de noţiuni sau de abstractizare. (pag. 3) Programele şcolare de matematică pentru clasele a V-a şi a VI-a se axează pe introducerea intuitivă a conceptelor matematice, fără utilizarea excesivă a formalismului specific matematicii (…) Clasa a V-a: (…) Abordarea elementelor de geometrie urmăreşte, cu precădere, dezvoltarea deprinderilor de utilizare a instrumentelor geometrice (pag. 31) Clasa a VI-a: Programa şcolară de matematică (…) continuă demersul început în clasa a V-a din punct de vedere al prezentării intuitive/ descriptive a noţiunilor (…) Tema Noţiuni geometrice fundamentale continuă introducerea realizată în clasa a V-a (…) în aceeaşi manieră, prin raportare la imagine, model, obiect, mediul înconjurător. (pag. 32)

P.S. (scurtă lecţie de germană) După finalizarea eseului am mai găsit un argument de ordin lingvistic în favoarea gradelor de unghi. Cuvântul pentru “raportor” în limba germană este Winkelmesser, cuvânt compus din Winkel însemnând “unghi” şi Messer însemnând “măsurător”, adică “măsurător de unghiuri”. Vedem că nu le spune Bogenmesser însemnând măsurător de arce. Deci, cu tot respectul faţă de memoria profesorului Hollinger, în disputa noastră cred că totuşi câştigă unghiul în faţa arcului. (denumirea românească pentru acest instrument este oricum irelevantă din punct de vedere al înţelegerii copilului).

CTG, 18 sept. 2018

De curând am primit o întrebare deosebit de clară despre acest subiect pe care de mult îmi doream să-l tratez. Îi mulţumesc pe această cale colegului (semnat Alex D.) pentru că „mi-a ridicat cum nu se putea mai bine le fileu” acest subiect. Iată întrebarea cu pricina:

Dacă introducem noţiunea de unghi mai întâi în forma unghiului la centru, ar fi de preferat să definim notiunea de grad întâi pentru arce de cerc şi să definim măsura unui unghi ca măsura arcului cuprins între laturi prin deschiderea unghiului, justificând astfel şi folosirea raportorului (studiind oarecum în paralel cercul şi unghiurile, cum am văzut în Manualul de a VI-a din ’69 de Rusu şi Hollinger)? Întrebarea apare în urma postării  părţii a 6-a a eseului despre folosirea intuiţiei în aranjarea materiei. Iată, pentru reamintire în următoarele două aliniate pasajul la care se referă probabil colegul.

Clasa a V-a, semestrul II: geometria poate fi începută în mod atractiv pentru micile minţi cu o serie de construcţii cu rigla şi compasul, pornind de la marea minune numită Floarea vieţii, o reprezentare cu tente profund artistice a împărţirii cercului în exact şase părţi egale cu compasul. Steaua lui David şi tot felul de combinaţii dintre acestea dau începutului de geometrie o tentă istorico mistică venită din vechime, oferind începutului de geometrie o atmosferă de poveste cu aspecte de manualitate şi multă înţelegere intuitivă într-o formă de gândire primitivă a fenomenului geometric. Acest capitol va conţine în continuare împărţirea cercului în 4 părţi egale, apoi în 8 şi în 12, toate realizate doar cu rigla şi compasul (…).

Pentru împărţirea cercului în cinci părţi egale se va introduce noţiunea de grad, plecând de la ideea împărţirii cercului în 360 de părţi (analogie cu anul de 365 de zile, idee apărută în vechime). Pe baza acestor gânduri se poate împărţi cercul cu raportorul centrat în centrul cercului (cel mai bine un raportor complet, de 360^o). Cu această metodă se pot face împărţiri ale cercului şi în 10 sau 9 părţi egale. Astfel, noţiunea de unghi apare natural, iniţial în forma unghiului la centrul cercului. În finalul acestui prim capitol se vor construi diferite stelări, elevii primind să măsoare şi unghiurile din vârful stelărilor, trebuind să caute diferite “legităţi” ce apar în aceste situaţii. Astfel unghiurile se eliberează de centrul cercului, elevul formând astfel în mintea sa această noţiune dificilă într-un mod natural, distractiv, construindu-le cu singurul obiectiv de a face desene frumoase. Aspectele teoretice se vor lăsa pe anul viitor, în clasa a V-a apărând doar titluri şi mici comentarii pe lângă desene, eventuale descrieri ale metodelor de realizare a construcţiilor. În această parte va fi introdus şi echerul, însă doar ca instrument de verificare a unghiului drept. Subunităţile gradului merită introduse aici imediat după lecţia despre unităţile şi subunităţile pentru măsurarea timpului. (…)

Primul lucru care îmi vine în minte legat de acest subiect este o întrebare al cărei răspuns îi dă un iz de banc, întrebare cu care-i surprind pe colegi de aproape 20 de ani: ce măsurăm în primul rând cu gradele? Unghiurile sau arcele de cerc? După părerea mea răspunsul este cât se poate de simplu şi totuşi surprinzător: Nici una, nici cealaltă! La origine, gradele măsoară rotaţia!

Permiteţi-mi să argumentez acest răspuns. Fizica se ocupă cu două tipuri de mişcare: mişcarea rectilinie şi rotaţia. Exprimat în modul cel mai simplu, orice mişcare este de obicei compunerea celor două tipuri. Cu unităţile de lungime măsurăm iniţial distanţa parcursă de un punct material ce se deplasează rectiliniu (apoi o adaptăm noi şi la mişcarea pe alte traiectorii decât rectilinii). În mod corespunzător ne trebuie şi o unitate de măsură pentru rotaţie (iniţial cea plană), iar aceasta este în şcoala noastră gradul sexazecimal.

Cât este de mare gradul? Prin convenţie o rotaţie completă a fost împărţită în 360 de părţi, acest număr fiind ales ca aproximarea cea mai bună din punct de vedere al calculelor pentru numărul de zile dintr-un an, aproximare venită din vechime. Deci, o rotaţie completă are 360^o. O jumătate de rotaţie are 180^o iar un sfert de rotaţie 90^o. Bine, veţi spune, şi dintre unghi şi arc, care are întâietate? Părerea mea este că nici unul nu este mai important. Diferă doar ordinea logică în care sunt folosite odată cu introducerea elementelor de materie şi parcurgerea claselor de studiu.

Astfel, paradigma în care actualmente „suntem acasă”, forma cu care suntem obişnuiţi, este următoarea: clasa a VI-a şi a VII-a (până spre final) sunt sub dominaţia totală a unghiului. În finalul clasei a VII-a apar pentru scurt timp arcele şi măsurile de arc, dar dispar apoi ca utilizare până prin liceu. Dar nici în liceu nu mai apar foarte clar, pentru că de 20 de ani a doua parcurgere, mai matură, a geometriei a fost scoasă (mă refer aici la marea învârtoşeală a patrulaterelor inscriptibile, a unghiurilor înscrise în cerc sau formate de o coardă cu o tangentă, a puterii punctului faţă de cerc etc.). Rămân doar vagi aplicaţii în zona trigonometrică, dar şi aici materia a fost algebrizată la maximum (mai nimeni nu mai predă cercul trigonometric şi justificările bazate pe geometrie ale respectivelor cunoştiinţe). Cine are nevoie de acestea la facultăţile tehnice – ghinion – să se descurce singur cum poate,  eventual în particular. Apropos cercul trigonometric: oare câţi ne gândim despre felul cum îi loveşte lipsa acestuia şi a justificărilor relaţiilor trigonometrice pe elevii cu o gândire bazată mai mult pe vizual şi pe raţionament spaţial? Vă zic eu: „ îi rupe”! Şi apoi ne plângem că n-a învăţat nimic copilul ăla. Ba nu! Noi nu i-am predat conform setării creierului său. Noi avem o materie prost concepută şi noi nu luăm măsuri de corectare minimală la clasă.. Noi suntem de vină, atât cei de la minister, cât şi cei de la clasă.

Deci, să ne lămurim, nu ia nimeni întâietatea unghiului (mă refer la întâietatea de preocupare prin ordinea materiei). Dar unghiul este o figură iniţial foarte abstractă. Una este să vorbeşti despre lungimea unui segment şi toţi copiii iau liniarul şi îl măsoară, şi alta este să le definim unghiul, iar apoi să le cerem imediat să-l măsoare. Gafa făcută în ultimii aproape 10 ani cu introducerea unghiului şi a măsurii sale în clasa a V-a prin mutarea simplă a lecţiei din clasa a VI-a este evidentă. Nu mă miră în acest context întrebarea unei colege în urmă cu mai mulţi ani: tu cum predai unghiurile? Că la mine elevii nu le înţeleg. (observase pe careva elevi de la mine din clase cu care se ocupase în particular, că ştiau unghiurile, le înţelegeau, le foloseau natural).

Această constatare ne duce tot mai aproape spre întrebarea: Bine, bine! Şi noi ce definim mai întâi? Arcul sau unghiul? Eu personal nici una nici cealaltă. În asta constă de fapt predarea intuitivă: să pleci de la ceva „intuitiv”, fără să defineşti acel ceva, să-l stabilizezi prin utilizare (ludică ar fi cel mai bine), iar apoi ulterior, cândva, la o viitoare abordare (predarea în spirală) să lămureşti lucrurile teoretic.

Ca să clarificăm această brambureală (nici un apropos, d-na Abramburica, subiectul acesta nu vă priveşte), să ne imaginăm cele două noţiuni în dispută, unghiurile şi arcele, poziţionate alături, fiecare cu pretenţiile sale de definire ca obiect şi ca unitate de măsură, iar undeva deasupra lor, dominându-le prin întâietate absolută: rotaţia. Elevul trebuie să primească în primul rând rotaţia, iar apoi imediat, dacă se poate chiar în paralel, cele două manifestări ale acesteia în fizic, unghiurile şi arcele. Înainte ca cel două noţiuni să se despartă, ele sunt încă împreună „în casa părintească”. Dar care este „casa părintească”? Pentru că rotaţia nu se poate reprezenta bine pe tablă ca o figură statică. Păi figura geometrică fizică în care se manifestă rotaţia este cercul, anume cercul trasat şi privit din centrul său (deci, nu un cerc desenat în jurul unei farfurioare). Rotaţia are un centru de rotaţie, iar manifestarea în planul fizic a rotaţiei o reprezintă cercul, instrumentul pentru vizualizarea acesteia fiind compasul. Iar dacă ne poziţionăm în centrul cercului şi ne rotim un pic, vom vedea că privirea noastră parcurge un unghi plecând de la poziţia iniţială şi până la noua poziţia, vorbesc de unghiul la centru, iar dacă întind mâna în faţă (ca o rază), vârful degetelor parcurg un arc de cerc, arcul subântins de acest unghi la centru. În timp ce mă rotesc, privirea mea parcurge un unghi, în timp ce capătul mâinii întinse parcurge un arc. Sper că aţi înţeles: eu fac aceste mişcări în faţa clasei cu mâna întinsă în faţă, întâi cele cu 360^o, 180^o şi 90^o, apoi ultima cu măsura oarecare, pe care apoi o desenez şi pe cercul de pe tablă.

După ce completez pe tablă ce am arătat prin mişcare fizică, le mai arăt încă o dată cu ajutorul compasului de tablă văzut ca o bună imagine pentru un unghi (am un compas vechi din lemn cu braţele drepte şi care se deschide până peste 270^o). Ţin compasul închis orizontal cu acul şi creta către stânga (elevii văd către dreapta) şi încep să-l deschid până la un moment când mă opresc şi îi privesc mândru: “acesta este un unghi, iar creta care se mişcă prin aer, dacă ar fi pe tablă ar descrie cercul respectiv”. Voi reveni la această exemplificare pentru vizualizarea unghiului, deschizând compasul ca pe un unghi, în clasa a VI-a când voi face clasificarea unghiurilor. Acolo eu fac o primă clasificare mai simplă (unghi ascuţit, drept şi obtuz), iar apoi una completă (unghi nul, ascuţit, drept, obtuz, alungit, supraobtuz şi unghi plin), ambele desenate pe tablă, dar şi arătate în aer prin deschiderea compasului privit ca un unghi.

Aşadar, mai întâi iau cercul ca manifestare a mişcării de rotaţie în planul tablei sau al caietului (se pot folosi chiar săgetuţe pe cerc care să arate mişcarea de rotaţie), iar apoi, din acesta, prin analiză a fenomenului, deduc unghiul la centru şi arcul de cerc, folosind ambele aceeaşi unitate de măsură: gradul ca măsură a rotaţiei. Aici se pot chiar introduce acele mici arce de cerc, uneori dublate sau chiar triplate, ce le punem în interiorul unghiului, aproape de vârful său, pentru a evidenţia unul sau altul dintre unghiuri. Sfatul meu este însă ca la primele utilizări să nu punem un simplu arc, ci de fapt un arc cu săgeată care să scoată în evidenţă rotaţia. Nu există un principiu „bătut în cuie”, dar eu pornesc în primele exemple de la poziţia cunoscută ca „originea cercului trigonometric”, adică punctul din partea dreaptă a cercului (îl putem denumi şi Est, prin analogie cu poziţia respectivă pe hărţile geografice), iar apoi rotaţia o pornesc în sens trigonometric, adică deschid unghiul sau arcul în sus. Desigur că elevilor nu le spun nimic din toate această ciudată „sădire a unor seminţe trigonometrice” (voi reveni din nou la poziţia specifică din cercul trigonometric, atunci când le voi explica apariţia raportului sinus dintre catetă şi ipotenuză într-un triunghi dreptunghic, în semestrul II din clasa a VII-a).

Măsurile le voi trece la început în paralel şi în vârful unghiului la centru şi pe arcul parte a cercului, la început deduse prin gândire, prin împărţirea cercului în părţi egale (cuvântul congruent îl introduc de-abia în clasa a VI-a). Concret, în primul rând voi lua un cerc împărţit în patru felii, ca la o pizza mică (noţiunea de sector de cerc poate şi aceasta să vină mai târziu), având trecut 90^o în fiecare colţ. Aici putem aduce pentru prima dată atât raportorul poziţionat cu centrul în centrul cercului, şi copiii să vadă că acolo sus scrie 90^o, dar şi echerul, copiii văzând cum echerul intră perfect în „unghiul drept”.