Cu ocazia acestui început de an (ian.-feb. 2019) am fost blagosloviţi de o nouă găselniţă venită “de sus”: o Scrisoare metodică elaborată de către membrii Comisiei Naţionale de Specialitate şi inspectorii şcolari pe disciplina matematică, sub coordonarea MEN şi a Societăţii de Ştiinţe Matematice. UAU!
Îmi cer scuze pentru limbajul agresiv-vulgar de mai sus, dar am vrut să joc un pic de teatru şi să exprim cam cum a fost percepută în şcoli, de către profesori, această nouă “mişcare” a ministerului: “Cum? Ce? Ce-au mai inventat?”. În unele şcoli poate că s-a întrunit catedra, în altele poate a fost însărcinat un coleg cu redactarea planului operaţional. Dar, despre ce-i vorba? Cine ştie ce a înţeles fiecare! Ar fi trebuit să fim convocaţi şi să fim lămuriţi despre ce şi cum. Sau poate nu? Pentru că la precedenta mişcare, la începutul clasei a V-a pe noua programă, ştim noi ce explicaţii am primit …
Permiteţi-mi să analizez mai profund această nouă “misivă”, această iniţiativă care, corect transpusă (!), s-ar putea dovedi piatra de hotar între trecutul matematicii şcolare utopic, aşa cum l-a dorit Ceauşescu şi un viitor matematic sănătos pentru majoritatea elevilor. Nu voi relua respectiva scrisoare metodică, ci doar fragmente din aceasta, în măsura necesităţii înţelegerii şi curgerii textului. Cititorii care nu sunt prezenţi sau activi actualmente în învăţământ, şi deci n-au avut ocazia de a o primi pe scară ierarhică, sunt rugaţi să o lectureze de pe postările site-urilor ISJ din ţară (introduceţi Scrisoare metodică 2019); la fel sunt rugaţi să facă şi colegii care nu au citit-o încă.
*
Pentru cei care n-au avut ocazia să lectureze diferitele mele eseuri legate de istoricul acestui subiect, permiteţi-mi să fac un scurt rezumat al acestor idei. (1) În diversele cărţi legate de forma matematicii şcolare publicate în anii 60-70 se găsesc numeroase mărturii ale luptei dintre metodişti şi teoreticieni Pe de o parte se situau cei care doreau impunerea unor teme noi în predare (cum ar fi teoria mulţimilor, dar şi multe noţiuni nerelevante pentru materia în cauză, dar necesare unei definiri mai riguroase, cum ar fi de pildă noţiunea de semiplan în clasa a VI-a pentru definirea interiorului unui unghi); aceştia doreau şi impunerea unei mult mai crescute rigurozităţi în prezentarea subiectelor la clasă, mai ales în exprimare, atât în cea scrisă cât şi în cea orală (axiomatizare, definire super-detaliată, scriere riguroasă, de pildă pe baza limbajului mulţimilor), o exprimare mult mai apropiată de forma academică în care se ajunsese în prima jumătate a secolului XX. De cealaltă parte se situau metodiştii, susţinători ai metodelor tradiţionale de predare verificate pe fiecare vârstă şcolară. Aceştia (printre care vârful se pare că îl reprezenta Profesorul Eugen Rusu) încercau să avertizeze de efectele negative ce vor apărea la elevi în cazul unor astfel de schimbări, luptându-se de pildă pentru păstrarea folosirii intuiţiei în predare.
(2) Olimpiada Internaţională de Matematică a fost organizată pentru prima oară în 1959 în România şi doar între ţări din blocul comunist; la fel şi a doua ediţie. Primele ediţii au reprezentat o afacere internă a sistemului comunist care se străduia să genereze o organizare mondială paralelă cu cea capitalistă. Doar spre finalul anilor ’60 au intrat în horă şi primele ţări capitaliste. În toată această perioadă România s-a situat constant între leaderii noii mişcări matematice inter-ţări, ocupând relativ constant locuri fruntaşe. De abia la începutul anilor ’70 au început să intre în concurs şi marile puteri capitaliste, în frunte cu SUA. Din acel moment lupta între cele două blocuri sociale s-a acutizat, ridicându-se la nivele ce au ajuns cvasi inaccesibile majorităţii participanţilor, lupta devenind una “pe viaţă şi pe moarte” între leaderii celor două blocuri, URSS şi SUA. În aceste condiţii, românii nu mai ajungeau pe primele locuri ale competiţiei.
(3) În preocupările sale, Ceauşescu a decis spre finalul anilor ’70 o reformă a învăţământului, mai ales a celui matematic, cu scopul explicit de a aduce din nou România pe locurile fruntaşe în OIM, dar şi în alte olimpiade internaţionale. Se întâmpla asta în marea strădanie de a aduce România pe locurile fruntaşe în toate competiţiile, desigur şi în cele sportive, pentru a dovedi teoriile sale fantasmagorice despre omul de tip nou specific societăţii socialiste multilateral dezvoltate bla-bla-bla. Pentru obţinerea rezultatelor dorite în matematică au fost aduşi la ordin atât reprezentanţii curentului teoreticienilor, cât şi responsabilii pentru pregătirea loturilor de olimpici. L-a fel ca şi în activităţile sportive, s-a organizat o foarte largă bază de preocupare şi selecţie. Materia şcolară a fost încărcată, îngreunată şi teoretizată, diferite lecţii au ajuns deseori în clase mai mici şi nivelul problemelor aplicative a început să crească constant. Toată această reformă s-a petrecut orientativ între 1977 şi 1981, iar noua linie a fost impusă cu forţa în deceniul ce a urmat până la căderea lui Ceauşescu. Chiar dacă în primii ani profesorii au rezistat, mai ales în cazul schimbărilor absurde din materie aceştia păstrând formele vechi de lecţii, cu timpul majoritatea au fost forţaţi să “se dea pe brazdă” sub presiunea inspectorilor şcolari. Ţinând cont că cei care au prins această reformă în activitate la catedră s-au cam pensionat sau chiar nu mai sunt printre noi, eu obişnuiesc să o numesc pe această Reforma uitată din 1980.
(4) La începutul anilor ’90 când celelalte ţări-satelit URSS în fostul bloc operau transformări structurale de eliberare de sub metodele şi principiile dictaturilor comuniste, noi, românii, eram mândri nevoie mare de “olimpicii şi sportivii noştri” şi nimănui nu-i trecea prin cap să pună în discuţie nivelul aberant al matematicii şcolare. Mai mult, în cadrul reformei din 1997 avântul teoreticisto-olimpic s-a păstrat, chiar s-a potenţat prin apariţia mai multor manuale paralele, scuzaţi, alternative, majoritatea dintre acestea crescând din nou nivelul, faţă de cele comuniste valabile din anii ’80, de la reforma deja uitată. Creşterea a avut loc mai ales în direcţia aplicativă, a dificultăţii problemelor. Cu această ocazie toată tradiţia de probleme de excelenţă din GM şi de la diferitele olimpiade s-a descărcat în noile manuale, nemailăsând loc exerciţiilor de bază pentru fixarea noţiunilor de către elevii obişnuiţi sau chiar slăbuţi la matematică. În loc să aibă loc un proces reparatoriu, dimpotrivă presiunea asupra profesorilor a crescut “exponenţial”: directorii îi presau pe profesori să aducă rezultate la olimpiadă pentru şcoală; sistemul le dădea salarii de merit celor cu rezultate, iar inspectorii şcolari organizau toată ziua concursuri şi centre de excelenţă. Toată lumea era în concurs cu toată lumea şi asta în numele unei paradigme impusă de Ceauşescu. Ne bucuram că am scăpat oficial de dictator şi de regimul său, dar îi trăiam cu bucurie viitorul, cel puţin cel matematic şcolar, aşa cum îl preconizase el. Copiii nu erau încă distruşi de televizor, iar rezultatele la olimpiade încă mai veneau, situaţia fiind similară cu sportul românesc unde sistemul a mers din inerţie încă un deceniu şi ceva după căderea lui Ceauşescu.
(5) Cândva în anii 2000 (eu aş spune orientativ 2004-2005) s-a cam terminat cu avântul general iar balanţa a început să se încline încet dar sigur în direcţia opusă: se auzeau tot mai des voci în favoarea elevilor de rând, iar elevii performanţi ca pe vremuri începeau să apară tot mai rar; elevii în general începeau să fie tot mai puţin dispuşi să-şi petreacă tot timpul învăţând lucruri cu grad redus de entertainment, fiind tot mai atraşi de consumul mass-media (TV, jocuri pe calculator şi, timid la început, dar tot mai sigur internetul). Au urmat încet, dar hotărât, diferite schimbări de programă care încercau să uşureze matematica şcolară, mai ales pe cea gimnazială. Cea mai stupidă dintre toate a fost, după părerea mea, mutarea sistemelor de ecuaţii din finalul clasei a VII-a în finalul clasei a VIII-a, dar la fel de distructivă a fost şi mutarea capitolului despre patrulatere din clasa a VI-a în clasa a VII-a, peste vacanţa mare. Şi totuşi plângerile se înteţeau şi în curând toată presa a început să se plângă la unison despre starea jalnică a şcolii româneşti. Da, şi cam aşa trăim de peste 10 ani.
Aceste gânduri se pot studia şi în eseurile mele din 2016, de găsit într-o variantă mai scurtă în postarea http://pentagonia.ro/reforma-uitata-o-scurta-descriere/ sau mai pe larg în postările http://pentagonia.ro/reforma-uitata-partea-i/ şi http://pentagonia.ro/reforma-uitata-partea-a-ii-a/.
Prin programa din 2017 s-a încercat o reformă reparatorie mai amplă, dar marea masă a profesorilor, inclusiv mulţi inspectori, nu o înţeleg. Nu înţeleg ce se întâmplă, pentru că toată lumea este încă setată conform paradigmei “olimpiade şi cocursuri” moştenită de la Ceauşescu şi îmbunătăţită prin manualele alternative de la finalul anilor ’90. Foarte mulţi profesori predau cât se poate de teoretizat şi aruncă în elevi cu probleme mult peste posibilităţile lor. Aşa au fost setaţi. Aşa a fost setată profesorimea de peste 30 de ani.
*
Ca urmare, s-a redactat această scrisoare metodică, pentru compunerea căreia au fost adunaţi împreună toţi cei care sunt într-un fel sau altul răspunzători de matematica şcolară. Haideţi să citim scrisoarea metodică acum, după ce am recapitulat istoricul predării matematicii şcolare, aşa cum am reuşit eu să-l reconstitui. Haideţi să spicuim împreună acest document (pentru conformitate, precizez că toate pasajele următoare scrise înclinat sunt citate din respectiva SCRISOARE METODICĂ). Documentul începe cu patru ŢINTE:
1) Asigurarea calităţii educaţiei prin centrarea activităţii didactice pe proces, în egală măsură cu centrarea pe rezultate.
Gânduri explicative: Decursul procesului didactic este la fel de important ca şi rezultatele acestuia (întrbare pentru cititor: oare de ce un proces didactic sănătos este la fel de valoros ca şi rezultatele procesului?). Nu ne interesează doar rezultatele; rezultatele cu orice preţ trebuie evitate; gândirea matematică se formează foarte bine în proces. Dimpotrivă, dându-i direct reţetele pentru a ajunge cât mai repede şi mai sus la aplicaţii de excelenţă, văduvim mintea elevului de procesul înţelegerii sursei ideilor şi a formării unei gândiri complete; dându-i direct reţeta de rezolvare pentru a economisi timp, îi tăiem elevului din timpul în care el ar trebui să-şi exerseze gândirea pe marile raţionamente ale matematicii. Predarea matematicii nu constă doar în a le da elevilor rapid reţete, procesul predării matematicii este în sine important pentru înţelegerea fenomenului studiat şi pentru formarea gândirii în ansamblul său. Profesorii de matematică trebuie să se concentreze şi pe procesul predării şi vor fi evaluaţi ca atare. S-au încheiat vremurile când doar rezultatele contau. Rezultatele deosebite se obţineau în general doar cu elevii buni, dar un proces bine construit îi ajută şi pe elevii de nivel mediu; cu elevii mediocrii se obţin mult mai greu rezultate, chiar şi la examinări, dar societatea a înţeles că formarea gândirii logice printr-un proces didactic sănătos are urmări pozitive în gândirea generală a populaţiei dincolo de simplele subiecte de examen (de pildă se educă oameni mai greu manipulabili de către politicieni, iar acest fapt în sine creşte valoarea medie a unei populaţii, a unei societăţi); atragerea elevilor în procesul activităţii didactice coborând parcursul acestuia la un nivel accesibil majorităţii le dă şi elevilor mediocri ocazia de a-şi îmbogăţi gândirea practicând raţionamente logice specifice matematicii, nu doar dresându-şi mintea în aplicarea unor reţete de rezolvare ce se vor da la evaluare.
Mai presus de toate aceste gânduri, eu cred însă că respectiva ţintă scoate în evidenţă răspunsul la întrebarea “pentru ce învăţăm matematica?”. Iar răspunsul nu este doar “pentru examene şi concursuri”. Nu, pe lângă acestea – a căror realitate nu o contestă nimeni – pe lângă acestea mai există un motiv, anume formarea unei gândiri deductive logico-raţionale care îl va însoţi şi îi va sluji viitorului adult toată viaţa sa, mai ales în viaţa extramatematică, în luarea unor decizii corecte şi juste. Iar acest stil de gândire nu se formează dându-i elevui reţete rapide pentru obţinerea unor rezultate bune (rezultate atât direct în probleme, cât şi rezultate la nivel superior, în performarea elevilor la concursuri şi examene), ci se formează în procesul construirii lecţiilor de matematică. Nu mă pot abţine aici să nu scot în evidenţă strădaniile mele din recenta serie de postări menită a scoate preconizata predare a Teoremei lui Pitagora în finalul clasei a VI-a din zona de eficienţă concentrată pe rezultate rapide (obţinute prin predarea simplă a reţetei) şi aducerea predării acesteia într-o formă de proces deductiv al activităţii didactice, chiar dacă într-o formă mai intuitivă şi mai infantilă decât demonstraţiile cu care eram obişnuiţi până acum.
2) Creşterea preocupării profesorilor pentru conştientizarea elevilor privind rolul matematicii, atât din perspectiva de utilizatori primari, în viaţa de zi cu zi, cât şi ca urmare a diversificării domeniilor profesionale în care noţiunile şi raţionamentele matematice sunt prezente şi sprijină realizarea de sarcini şi acţiuni.
Gânduri explicative: Acest ţel conectează direct cu cele spuse în finalul comentariului la ţelul precedent, doar că schimbă un pic întrebarea: “la ce ne trebuie matematica?” în loc de “pentru ce învăţăm matematica?”. Oricum, şi aici extinderea este clară: nu învăţăm matematica doar pentru concursuri şi examene, ci – direcţia este de data asta chiar dată “mură-n gură” – de matematică avem nevoie în viaţa de zi cu zi (o mai ţineţi minte pe caseriţa din vară cu cele opt boxuri de apă minerală a câte şase butelii fiecare, în total 40 de butelii?), dar şi în multe specializări profesionale şi în îndeplinirea sarcinilor de serviciu ulterioare. Profesorii trebuie să se străduiască mai mult în acest sens; de fapt nu mai ajung argumente de tipul “vă trebuie la examen”. Ce nu s-a spus în redactarea acestui al doilea ţel este faptul că, pe lângă marea masă a facultăţilor ce includ şi cursuri de matematică, gândirea raţională logico-deductivă este de fapt necesară şi în majoritatea specializărilor care nici măcar nu se declară utilizatoare de matematică.
Încercând să luăm nişte exemple, mă gândesc că un pictor sau un muzician virtuoz chiar nu prea au nevoie în meseria lor de gândire raţională, dar un psihiatru care nu şi-a format o gândire logico-deductivă poate reprezenta uneori chiar un pericol pentru pacienţii săi (acest tip de psihiatri par din păcate majoritari). Ca o anecdotă, din cei doi psihiatri (psihologi, sau cum s-or fi mai numind) întâlniţi în şcoala noastră de-a lungul anilor la care am observat clar o gândire cu adevărat sănătoasă, una avea la activ şi facultatea de matematică.
Revenind la lucruri serioase, mă gândesc cât de important este ca viitoarele învăţătoare să aibă o relaţie pozitivă cu matematica, ele ca formatoare de bază a gândirii logice la viitoarele generaţii de copii. Din păcate însă, situaţia este cu totul alta: la PIPP nu ajung persoane care să fi avut o foarte bună relaţie cu gândirea logică, cursul de matematică ce le este adresat nu este privit ca important, având mari şanse să-şi rateze misiunea, iar mai departe nu are rost să discutăm, fiind evidentă forma deficitară a primilor paşi în formarea gândirii matematice la viitoarele clase primare (groaznică spirală a decăderii gândirii logice!).
3) Identificarea corectă a nevoilor de activităţi remediale, proiectarea şi desfăşurarea unor activităţi specifice, eficiente, cu accent pe formarea / dezvoltarea graduală a competenţelor (remedierea vizează îmbunătăţirea nivelului de competenţă, conţinuturile fiind suport al competenţelor).
Gânduri explicative: Nu am nimic cu activităţile remediale, nu neg rolul acestora, care este deosebit de important în multe cazuri, dar “gândesc şi eu în gura mare”: când vom ajunge să ne referim la activităţi de prevenţie a “avarierii matematice” a elevilor? De ce nu vorbim despre Identificarea corectă a nevoilor de activităţi preventive? Cum ar trebui să arate predarea matematicii structurată într-o formă preventivă? Ca să citez o reclamă simpatică difuzată la televizor: “aşa ceva, nu există!” (un individ holbându-se pe telefonul prietenului la site-ul Publi24). Dar, cum ar trebui să predăm astfel încât să acţionăm preventiv? Preventiv la ce? Păi, să încercăm să prevenim apariţia avarierii matematice a elevilor, rămânerile în urmă faţă de colegi şi apariţia blocajelor în gândire, clacarea în viaţă a unor copii în principiu sănătoşi şi fără defecte vizibile la nivelul gândirii. Acestea trebuie prevenite printr-o predare sănătoasă. Desigur că o astfel de predare este mare consumatoare de timp şi de obicei profesorii nici nu se gândesc să abordeze astfel de metode preventive pentru că setarea lor a fost în ultimii 30-40 de ani să tot fugă prin materie, să facă cât mai mult şi cât mai greu pentru a performa în zona de concursuri şi examene. În această paradigmă au fost împinşi, la început în anii ‘80 forţat, apoi din anii ’90 sub titluri de performanţă şi excelenţă (mândri că suntem români, noi şi olimpicii noştri etc.). Atunci când nu vom mai vedea clasamente cu cele mai bune şcoli la olimpiade sau examene, atunci vom şti că societatea este vindecată şi are rost să vorbim despre forme de predare conţinând activităţi preventive şi nu doar activităţi remediale. Până atunci acest blog pentagonia.ro va rămâne o pasăre rară şi oarecum ciudată în peisajul şcolar matematic din ţara noastră.
4) Aplicarea conformă a curriculumului (având în vedere zona dezvoltării proximale) în relaţie directă cu particularităţile colectivelor de elevi, nevoile şi stilurile de învăţare ale acestora, favorizând creşterea participării active la propria învăţare, diminuarea abandonului şcolar sau pasivităţii faţă de educaţie şi îmbunătăţirea rezultatelor învăţării, atât reflectate în rezultate la examene, evaluări, concursuri şi olimpiade şcolare de specialitate, cât şi în termeni de reuşită profesională şi socială.
Gânduri explicative: Încet, dar sigur, ies la iveală felul în care s-a predat la clase în primul an de introducere a noii programe, în anul şcolar 2017-2018 la clasele a V-a, dar şi în actualul an şcolar 2018-2019 până acum la clasele a VI-a. Ies la iveală situaţiile în care profesorii au acţionat distructiv la adresa majorităţii elevilor din clasă, în numele vechii paradigme care le îndrepta atenţia doar spre “elevii cei mai buni din clasă”, în numele obţinerii unor rezultate cât mai bune la sistemul de olimpiade, aceşti profesori acţionând abuziv şi distructiv la adresa celorlalţi elevi (să le spunem “restul de 90%”), agresându-i cu probleme foarte grele, mult peste nivelul vârstei şi al colectivului de elevi, dar şi cu un mod de predare a noilor cunoştiinţe cât mai abstract, teoreticist, neadaptat vârstei, deseori importat din clasele mai mari, uneori chiar din liceu (deci cu salt de vârstă chiar de 4 ani). Deseori programa nu a fost respectată, de pildă majoritatea profesorilor făcând în continuare ecuaţii în clasa a V-a, pur şi simplu pentru că nu erau pregătiţi în a parcurge problemele aritmetice prin metode specifice, fără punerea în ecuaţie, deşi noua programă o cerea explicit. În paradigma cu care s-au obişnuit, majoritatea profesorilor au nevoie de ecuaţii pentru rezolvarea situaţiilor întâlnite, iar lipsa acestora pur şi simplu nu funcţionează în acord cu pregătirea olimpiadelor aşa cum se pricep aceştia. Am întâlnit chiar un caz în care profesoara a predat în clasa a V-a într-o singură oră numerele întregi, inclusiv toate operaţiile, cu motivaţia că “să fie dacă se dă la olimpiadă”.
În şcolile bune din mediul urban nu prea apare abandonul şcolar, dar pasivitatea, chiar repulsia faţă de matematică este omniprezentă. Există clase întregi în care toţi părinţii plătesc ore particulare copiilor doar pentru că predarea profesorului nu este adaptată nevoilor reale ale vârstei şi particularităţilor colectivului de elevi, profesorul predând de fapt doar pentru “elevii cei mai buni din clasă” care urmează a merge la olimpiadă şi a reprezenta şcoala în mod onorabil (fiecare, cum şi ce înţelege prin onorabil). În nici un caz o astfel de abordare nu favorizează creşterea participării active a elevilor la propria învăţare. Cât despre reuşita profesională şi socială, am atins acest subiect în analiza celorlalte ţeluri. Se vede cum toate sunt profund interconectate, dar nimeni nu vorbeşte despre sursa cauzală a tuturor problemelor actuale ale predării matematicii şcolare în România.
Aşa văd eu lucrurile, acesta este punctul meu de vedere, iar cele de mai sus reprezintă o foarte scurtă analiză, în care am încercat să ating doar câteva aspecte vizate de către Scrisoarea metodică din acest punct de vedere. Mi-ar place să n-am dreptate, să fie totul doar o simplă şi isterică exagerare, dar toate aspectele converg către astfel de concluzii. Dvs., stimaţi cititori, cum vedeţi lucrurile? Este evident că analiza se cere continuată, aşa că voi încerca să revin cât de curând, în măsura timpului disponibil.
Prof. Constantin Titus Grigorovici
P.S. Pentru cititorii care ar fi tentaţi să conteste aceste gânduri, considerând că elevii nu sunt abuzaţi prin predarea matematicii în gimnaziu, daţi-mi voie să vă prezint câteva exemple din ultima perioadă.
Perimetrul unui triunghi este egal cu 60 cm iar raza cercului înscris în triunghi este egală cu 4 cm. Aria triunghiului este egală cu … cm2. Problema este preluată de pe site-ul mate.info.ro profu’ de mate, de pe unul din testele având ca titlu TEST model NR. 3 – Pregătire pentru simulare E.N. Proba scrisă la matematică clasa a VII-a, 13 martie 2019. Formula S = p ∙ r este în materia de clasa a VII-a şi trebuia să o facem? Sau nu este? Sau o fac diverse persoane ca un prim pas de introducere sub umbrela excelenţei? Dar atunci, ce căuta pe acest “model” de simulare? Oricum, în isteria creată de lipsa unor modele oficiale pentru simularea pripit organizată la clasa a VII-a, lumea a ajuns uşor la aceste modele şi întrebările despre ele circulau de zor.
Dar nu numai prin probleme din afara materiei sunt agrasaţi elevii, ci chiar şi prin lecţii. Un exemplu în acest sens ar fi studiul despre progresii în clasa a V-a, de către profesori tare ambiţioşi: una este să numeri aditiv sau multiplicativ din 2 în 2 sau din 3 în 3, sau chiar din ½ în ½ şi să pui câteva întrebări despre diferite momente ale acestui fenomen, şi alta este să imporţi cu totul lecţia din clasa a IX-a, cu toată abordarea teoretică, dar mai ales cu toată zestrea de probleme, şi asta în numele excelenţei şi al performanţei la olimpiade. Acesta este un exemplu cu salt de vârstă de patru ani în jos. Şi la alte materii se întâmplă astfel de preluări în bloc de la clase mai mari. Cunosc despre înclinaţia pentru astfel de acţiuni o situaţie din anul şcolar 2000-2001. Pe vremea respectivă eram dirginte la o clasă de a VIII-a, iar elevii trebuiau să se pregătească pentru nou introdusele probe la geografie şi istorie în cadrul Examenului de Capacitate. O elevă avea soră mai mare cu 5 ani, iar mama lor mi-a atras atenţia că testele după care se pregăteşte “asta mică” sunt aceleaşi teste după care s-a pregătit cu un an în urmă sora cea mare pentru examenul de Bacalaureat.
Cât despre prezentările teoretice, pentru cititorii care consideră că exagerez, că aceste descrieri sunt fabulaţii, că de fapt nu se exagerează, daţi-mi voie să vă prezint un exemplu concret din această iarnă, găsit în caietul unui elev. Este vorba despre primii paşi în lecţia Proporţionalitatea inversă (indirectă). După acest titlu apar scrise imediat următoarele rânduri, fără cuvinte de legătură sau alte explicaţii, în pur stil minimalist matematicist:
{ a1 , a2 , … , an } şi { bn , bn-1 , … , b2 , b1 } i.p.
a1 < a2 < … < an bn < bn-1 < … < b2 < b1
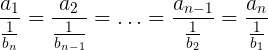
Aici ar trebui să spun: g.e.d.! Totuşi nu mă pot abţine, aşa că întreb: la ce bun toate astea? La ce îi poate ajuta pe elevii de clasa a VI-a o astfel de definiţie (incluzând renumitele “…”, puncte-puncte, la care majoritatea elevilor reacţionează cu spaimă în glas: “Suma lui Gauss?”) şi cu această îngâmfată etalare de scriere generalizată pentru n numere, care în plus, la proporţionalitea inversă – în cazul absolutizării ordonării celor două mulţimi de numere, neapărat în ordine crescătoare – impune tratarea elementelor celei de a doua mulţimi de la coadă (bn < bn-1 < … < b2 < b1). Mă mai puteţi urmări? Da’ de elevi ce să mai zicem!? Toate acestea se adaugă în dificultate situaţiei oricum dificile generate de forma condiţionării proporţionalităţii inverse cu fracţii supraetajate (am scris despre aceasta în postarea http://pentagonia.ro/maimutele-si-educatia/ , pe vremea când credeam că mai rău nu se poate). Ce-ar fi fost dacă definiţia s-ar fi dat doar pentru trei elemente, să zicem {a, b, c} şi {x, y, z} sunt i.p etc.? Ce a obţinut cadrul didactic respectiv în sufletul elevilor săi? Cum s-au dus aceşti copii acasă din punct de vedere al încrederii în sine. Vă las pe dvs. să alegeţi un răspuns la aceaste întrebări. Eu mă gândesc doar dacă nu trebuia să folosesc mai degrabă denumirea “antididactic”.
