Iepuraşii lui Fibonacci

În grupul celor mai spectaculoase şi mai cunoscute probleme de matematică sunt aglomerate de fapt mai multe “vedete”, realizarea unei ierarhii stricte între acestea fiind practic imposibilă. Totuşi, chiar dacă pentru unii s-ar putea să nu reprezinte vârful unei astfel de selecţii, problema lui Fibonacci cu iepuraşii este sigur în “top 10” al celor mai frumoase probleme din toate timpurile, şi nu fac această afirmaţie doar din punct de vedere al multitudinii de aplicaţii a şirului numerelor lui Fibonacci. Problema în sine este frumoasă, deosebit de provicatoare pentru gândirea umană în general, dar şi în particular pentru persoana (elevul) care primeşte spre rezolvare problema fără a-i cunoaşte răspunsul şi algoritmul aritmetic de generare a numerelor. Dar nu numai atât, problema reprezintă o provocare serioasă chiar şi pentru profesorul de matematică, care cunoaşte atât răspunsul (şirul lui Fibonacci) cât şi forma relativă a problemei: cum se deduce însă din problema iepuraşilor proprietatea caracteristică de generare a şirului cu pricina?

Acestor întrebări trebuie neapărat să le mai adăugăm una de ordin pedagogic: în ce clasă ar fi potrivit să propunem această problemă elevilor? Şirul lui Fibonacci apare în liceu la clasele de real în studiul şirurilor. Oare nu ar trebui să apară şi la clasele de uman? Dar problema în sine cu iepuraşi nu apare niciunde. De ce? Ce are această problemă, de profesorii nu se gândesc să o facă? Nici profesorii individual, nici organizatorii de programe, dar nici autorii de manuale (nu am o pasiune deosebită de a colectoa toate manualele ce apar, dar oricum nu am ştiinţă să existe într-un manual oficial; dacă există îmi cer scuze). Revin la intrebare: în ce clasă ar fi potrivit de făcut această problemă?

Eu nu deţin neapărat un răspuns hotărât la această întrebare, dar ştiu sigur că a lăsa elevii să plece din şcoală fără să fi cunoscut această problemă este mare păcat. Un argument în favoarea acestei afirmaţii este faptul că numerele lui Fibonacci sunt unele dintre destul de puţinele situaţii matematice care au penetrat cultura universală, prezenţa acestora în renumitul roman Codul lui da Vinci fiind doar un exemplu în acest sens.

Problema apare în cartea Liber abacci a lui  Leonardo Pissaro, zis şi Fibonacci, în a doua ediţie a acesteia din 1204. Iată o cât de cât curată variantă a problemei: Într-o curte sunt aduşi o pereche de iepuraşi pui (un băieţel şi o fetiţă). Pui de iepuri se maturizează într-o lună. După maturizare încep să facă pui, sarcina durând o lună şi fiecare naştere aduce pe lume o pereche de pui (un băieţel şi o fetiţă). Aceştia se maturizează într-o lună şi după încă o lună de sarcină au şi ei pui (întotdeauna o pereche). Adulţii aduc pe lume după fiecare lună câte o pereche de pui. Câte perechi de iepuri vor fi după un an?

Câţiva ani la rând am prezentat această problemă la clase liceale de uman, folosind farmecul deosebit exercitat chiar şi asupra ne-matematicienilor. Astfel, probelma poate fi prezentată într-o formă liberă de orice constrângere de rigurozitate scriptică a unei lecţii matematice anume. Ţinând cont că elevii de la uman nu au o deosebită capacitate de imaginaţie şi înţelegere a unor situaţii, capacitate necesară pentru găsirea numerelor şi pentru sintetizarea modelului comportamental al acestor numere, am căutat o cale cât mai atractivă de a le aduce în faţă problema.

Concret, am strâns de-a lungul anilor un sac de iepuraşi din pluş, mai mari sau mai mici, cu care fac elevilor o prezentare simulată a situaţiei descrisă în problemă (elevilor trebuie să le atragem atenţia de câteva ori că vom prezenta situaţia cu un iepuraş, gândind însă că este vorba despre o pereche (!). Astfel, încep prin a le pune pe masă un iepuraş mic (1). În pasul al doilea, adică “după o lună” înlocuiesc acest iepuraş cu unul mare (din sacul cu iepuraşi de pluş de pe masă), adică tot (1). După “încă o lună” aceştia capătă pui, deci pe lângă iepuraşul mare mai scot şi unul mic pe masă (2). După “încă o lună” noii pui se maturizează (îl înlocuiesc pe cel mic cu unul mare), iar cei iniţiali mai au o pereche de pui (scot din nou un iepuraşi mic), având pe masă doi iepuri mari şi unul mic (3). Peste “încă o lună” înlocuiesc iepuraşul mic cu unul mare şi în paralel scot din sac doi iepuraşi mici, ca reprezentanţi ai celor două perechi de pui ai celor două perechi deja adulte, având astfel pe masă trei iepuri mari şi doi mici (5). În general reuşesc să merg încă doi-trei paşi, (8) şi (13), cel mult (21), într-o cascadă de iepuraşi care tot “ies din sac”, după care mă opresc în râsetele generale ale audienţei. Iată în acest sens o “poză de grup” de la una din ultimele “reprezentaţii” ale problemei.

Las câteva momente de râs general apoi, după liniştirea atmosferei, elevii primesc sarcina să încerce pe caiete o formă de contabilizare pe paşi a numărului de iepuraşi (şi aici trebuie repetat că scriem 1 şi înţelegem o pereche de iepuri). În funcţie de timpul alocat, în final încerc întotdeauna la tablă realizarea unei scheme care să arate în ce fel evoluează numărul iepuraşilor, iar la marginea acestei scheme scriem la fiecare nivel numărul corespunzător acestei etape. Este evident că nu putem merge foarte mulţi paşi pentru că diagrama creşte puternic, aşa că destul de repede elevii trebuie să facă transferul de concentrare de la diagramă la numerele alăturate şi să “observe” modelul comportamental aritmetic după care apar acestea. În final facem un tabel separat cu 13 poziţii (start + 12 luni), în care cuprindem numerele obţinute şi îl completăm până la capăt. Iată şi o variantă de diagramă găsită pe net ca sugestie de lucru (să nu vă tot arăt variantele pusă de mine pe tablă). Spre deosebire de alte imagini ce se găsesc pe net, aceasta scoate în evidenţă atăt ideea de pereche, cât şi prin linie continuă o anumită pereche de iepuri, respectiv prin linie întreruptă naşterea unei noi perechi.

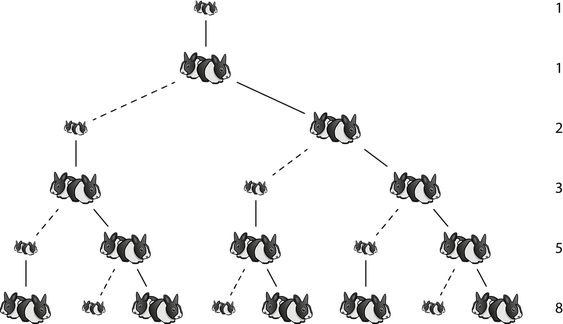
După cum am mai scris, iarna aceasta am cunoscut cartea Drăcuşorul cifrelor în care problema apare într-o formă foarte accesibilă elevilor de gimnaziu. Şi în desenele din carte sunt prezentaţi iepuraşii dublaţi (deci ca pereche) astfel încât este rezolvată şi situaţia disonantă că numerele lui Fibinacci se referă la perechile de iepuri (nu câţi iepuri, ci câte perechi). Ca semn de apreciere faţă de elevul din clasa a VII-a care mi-a împrumutat cartea înainte de vacanţă, am prezentat clasei respective această problemă în prima oră după vacanţa de iarnă (şi a mers foarte bine, deci în această formă jucăuşă funcţionează foarte bine şi la gimnaziu).

Lecţia funcţionează însă foarte bine şi la adulţi ne-matematici. La inceputul lunii decembrie am prezentat-o într-o întâlnire a Consiliului profesoral, la partea pedagogică, iar colegii (învăţătoare şi profesori de toate materiile) au reacţionat la fel de pozitiv ca şi elevii. Mai mult, o colegă mi-a dăruit înainte de vacanţă un tricou pe care desenase o grămadă de iepuraşi şi numerele lui Fibonacci. Cu mulţumirile de rigoare vă prezint şi dvs. desenul de pe acel tricou. Titus şi iepuraşii