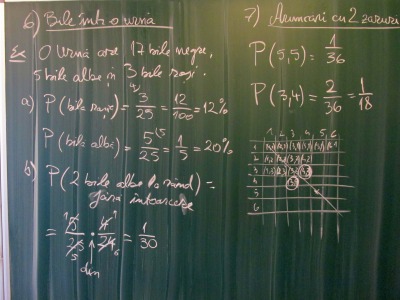Ideea predării probabilităţilor chiar din clasele mici gimnaziale este în sine o idee năstruşnică prin prisma următorului gând: probabilităţile sunt un fenomen matematic ce ţine exclusiv de viitor, de anticiparea viitorului, pe când gândirea copiilor este profund ancorată în prezent. Urmare a acestui aspect ar rezulta că subiectul calculării probabilităţilor nu este unul de a V-a, ci mai degrabă unul de final de a VI-a, chiar poate de a VII-a. Pe vremuri probabilităţile se studiau doar în liceu. Oricum, această lecţie este una destul de liberă, nelegată în mod special de altele, decât prin faptul că trebuie să fi fost studiate deja rapoartele şi procentele. Vreau să spun prin aceasta că lecţia nu are alte îngrădiri de ordin structural matematic, putând fi astfel poziţionată oricând (ea se face într-un anumit punct al programei doar pentru că aşa s-a convenit, nu pentru că ar fi matematic obligatoriu acolo).
Oricum, tema ar trebui abordate prin prisma gândurilor pedagogic naturale că trebuie să o luăm de jos, cât mai de jos, cu răbdare şi multe exemple, pentru a nu pierde elevi pe drum chiar de la început. Nu susţin că aşa nu pierzi elevi pe drum (cel care nu vrea să fie atent tot nu va pricepe nimic din noua temă), cum nu vreau să susţin nici că toţi elevii vor înţelege totul (lecţia va fi dusă tot de către elevii buni, cei care duc de obicei toate lecţiile). Dar măcar o astfel de abordare asigură faptul că las portiţa deschisă şi toţi elevii au ocazia să participe, pentru că aceste cunoştinţe nu presupun multe altele anterior bine dobândite. Piviţi mai întâi pozele lecţiei pe tablă:
După cum simţiţi, lecţia are un profund caracter ludic, deşi eu nu am aruncat nici măcar o dată cu un zar sau cu o monedă pe parcursul acestei ore. Toţi elevii au văzut cum este să arunci cu zarul sau cum se aruncă la începutul unui meci cu moneda pentru a se stabili terenurile fiecărei echipe. Desigur că dvs. trebuie să vă imaginaţi dialogul constant cu clasa, a cărui umbră apar cele scrise pe tablă şi în caiete. Întreaga lecţie a fost prezentată sub formă de întrebări, descoperirea acesteia, generarea lecţiei prin problematizare făcând-o foarte atractivă pentru elevi; până acolo de atractivă încât nu a mai fost nevoie de nici o definiţie, de nici o formulă de calcul a probabilităţii. La o oră ulterioară, eventual sub forma unei analize retrospective mai teoretice se poate da şi o definiţie (cazuri favorabile supra …).
Am spus că nu am aruncat cu zaruri,dar am scos din pungă acele zaruri ciudate cu 12 sau cu 20 de feţe, prezentându-le elevilor ca să ştie despre ce este vorba (dvs. le cunoaşteţi din postări mai vechi pe acest blog). Calendarul dodecaedric nu l-am avut în clasă, dar l-am descris şi elevii n-au avut nici o problemă în a răspunde cerinţelor. La aruncarea cu un calendar dodecaedric trebuie să explic întrebările, care au fost doar orale: probabilitatea să ne iasă o lună care începe cu litera i; probabilitatea să ne iasă o lună cu 31 zile; probabilitatea să ne iasă o lună care are numele de la un număr (octombrie vine de la 8); probabilitatea să ne iasă o lună care are numele de la un împărat roman (iulie de la Iulius Ceasar; august de la Augustus Ceasar).
Atrag atenţia asupra modului repetitiv “again and again” în care curg exemplele lecţiei, oferind astfel majorităţii elevilor suficient timp pentru a se acomoda cu noile cunoştiinţe, cu noua tipologie a scrierii. Doar elevii brilianţi în ale matematicii au capacitatea de a pricepe “din prima” o lecţie nouă. Ceilalţi au nevoie de multe exemple şi exerciţii până prind noua mişcare, cu toate aspectele ei, iar noi, profesorii, trebuie să pricepem acest fapt, altfel vom rămâne în continuare “o castă” de ciudaţi care chinuie copiii şi împotriva căreia se vor răscula tot mai des şi tot mai puternic părţi tot mai mari din societate.
Lecţia mai bifează un aspect important: ieşirea matematicii din zona sa internă de confort, prin apelarea atât la zarurile neobişnuite cu 12 sau 20 de feţe (am arătat că există şi cu 8 sau cu 10 feţe), cât şi prin folosirea minunatului exemplu al calendarului dodecaedric, cu scurte incursiuni în afara matematicii (nu aş merge până la folosirea termenilor de interdisciplinaritate sau transdisciplinaritate – Doamne cât ne mai plac termenii teoretici care-i dau pe spate pe cei din jur! – dar se simte totuşi un iz din acestea).
Legat de exemplul aruncării cu două zaruri, elevii trebuie ajutaţi să înţeleagă folosind două aspect. Mai întâi faptul că “să ne imaginăm că” aruncăm cu două zaruri de culori diferite (de ex. unul roşu şi unul albastru). Astfel vor înţelege că există doar un eveniment (5, 5), dar că există două evenimente cu 3 şi 4, adică (3, 4) şi (4, 3). Acest fapt este apoi “cristalizat” într-un tabel pătrat din care deducem că există 36 de cazuri teoretic posibile.
Mai rămâne de lămurit un singur aspect, cel evocat la început: de ce nu am aruncat cu zaruri? Pe lângă faptul că o oră de aruncat cu zarurile, o oră de tip “laborator de matematică”, s-ar fi lungit dincolo de limitele orei de clasă, există un aspect foarte important: prin faptul că i-am forţat pe elevi să-şi imagineze, deşi de fapt nu le-am arătat nimic, i-am forţat pe elevi să-şi folosească imaginaţia. Acest aspect este foarte important într-o lume plină de ecrane în care copiii de la vârstele cele mai fragede nu-şi mai folosesc imaginaţia pentru că primesc direct povestea prin intermediul imaginilor. Nu mai este ca pe vremuri când copilului i se spunea o poveste, iar mintiuca lui trebuia să-şi imagineze cele povestite oral, antrenându-se să-şi creeze astfel propriul său film interior. Astfel, mai ales o temă aranjată atât de atractiv, care are la bază experienţe ale elevilor din afara şcolii, trebuie neapărat folosită ca ocazie pentru antrenarea imaginaţiei.
P.S. Cu ocazia Centenarului Marii Uniri am gândit şi am scris un articol de analiză a situaţiei învăţământului matematic din România, sub gândul Unde suntem şi cum întâmpinăm Centenarul. Din păcat, ce a ieşit este destul de supărat, departe de orice atitudine festivă potrivită momentului. Riscam să obţin doar o imagine tip Cristian Tudor Popescu. Ca urmare, acest eseu a ajuns în arhivă, în aşteptarea unei forme mai pozitive de exprimare a gândurilor respective. În lipsă de altceva aţi avut ocazia să citiţi prezentarea lecţiei despre probabilităţi. C.T.G.