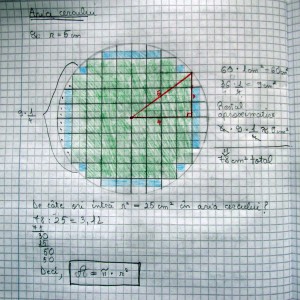
Exemplul 7: Adunarea fracţiilor
Exemplul 8: Sisteme de ecuaţii
Despre subiectul matematicii naive cred că am spus destul de multe încât să se înţeleagă despre ce este vorba. Totuşi, revin cu încă o tură de exemple, datorită unui comentariu din data de 02.06.2016, făcut de către un domn profesor pe site-ul didactic.ro la zona de dezbatere a noilor programe. Dânsul zice acolo: Eu cred ca scoaterea c.m.m.m.c. de la clasa a V-a. Aflarea numitorului comun prin ghiciri şi încercări, pentru a putea aduna două fracţii, nu mai seamănă a matematică.
Aici este evidentă neînţelegerea la nivelul profesorilor a adaptării predării la nivelul vârstei, cauzată de faptul că “programă din 2009” nu a fost însoţită şi de indicaţii metodico-didactice în care să se explice “noua linie de predare”. Iată cum am înţeles eu predarea la adunarea fracţiilor în contextul acestui subiect şi al acestei programe (când mă refer la adunare, subînţeleg desigur şi scăderea).
Într-o primă etapă, în clasa a IV-a, elevii învaţă cu doamnele învăţătoare adunarea fracţiilor cu acelaşi numitor (pe germană se spune gleichnamig, adică cele cu acelaşi nume). În a doua etapă, în clasa a V-a, se aduc fracţiile la acelaşi numitor în mod intuitiv, în forme de la simplu la tot mai complicate. În final, pentru cazurile cele mai dificile, unde intuiţia nu mai face faţă, parcurgem în clasa a VI-a găsirea c.m.m.m.c., cu care aflăm numitorul comun în format “automatizat”.
Este clar că, în comentariul de pe didactic.ro, e vorba despre etapa a doua. În această etapă elevii nu găsesc numitorul comun prin ghiciri şi încercări, ci prin pură înţelegere matematică intuitivă a numerelor, a fenomenului fracţiilor, aplicând proaspăt învăţata amplificare. Problema este însă, cum privim copilul? Îl privim ca pe un sac gol în care noi, profesorii trebuie să turnăm cunoştinţe, sau îl privim ca pe un om care gândeşte singur şi noi trebuie doar prin natura sarcinilor şi a provocărilor să-i cauzăm, să-i pornim gândirea? Îi dăm noi cunoştinţele respective, sau îl ajutăm pe el să le genereze? Îi dăm în fiecare zi un peşte, sau îl învăţăm să pescuiască? Aici am ajuns din nou la opoziţia dintre matematica rezultat, oferită elevului sub forma unei scurte prelegeri (la adunarea fracţiilor se procedează astfel: …), pe de-o parte, şi matematica proces, în care elevul este atras să o descopere singur prin problematizare (oare ce-ar trebui să face aici ca să putem aduna aceste fracţii?), pe de cealaltă parte.
Sigur, aici ajută un pic de explicaţii grafice: de pildă, a reprezenta o jumătate sub forma unui semidisc care, împărţit în trei părţi egale, arată cum se ajunge la 3/6. Alegerea primelor exemple este însă determinantă în procesul de înţelegere al elevilor. În acest sens eu practic o predare prin descoperire, în care elevii găsesc singuri cum să rezolve exerciţiile propuse, în timp ce eu ridic treptat ştacheta dificultăţii. Iată o posibilitate de ordonare a primelor exerciţii pe nivele de modele:
Modelul 0: recapitulare din clasa a IV-a;
Modelul 1: 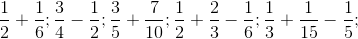 eventual
eventual 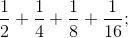 etc.
etc.
Modelul 2: 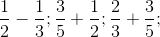 eventual, până la situaţii “extreme”
eventual, până la situaţii “extreme” 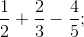 etc.
etc.
Modelul 3: 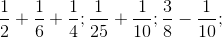 etc.
etc.
Probabil că la primul exerciţiu de la modelul 1 trebuie ajutată clasa s[ facă primul pas, “traducând” elevilor împărţirea de mai sus a jumătăţii în trei şesimi, într-o amplificare. La următoarele elevii intră în joc imediat şi ştiu ce să facă în continuare.
La modelul 3 se poate urca atâta cât “duc” elevii, oricum rămânănd în zona de numere accesibile calculului în cap. Pe această cale, elevii învaţă adunarea/ scăderea fracţiilor ca fenomen în clasa a V-a pe exemple accesibile, urmând ca formele complicate, cazurile grele, să le parcurgă în clasa a VI-a, după învăţarea găsirii c.m.m.m.c. prin reţeta oficială. Astfel, cunoaştem fenomenul în forma sa naivă, apoi îl aprofundăm în forma riguroasă la o a doua trecere (predarea în spirală).
Revenirea la subiectul matematicii naive, pe exemplul adunării fracţiilor din clasa a V-a, această revenire îmi oferă ocazia de a aborda încă o temă mult dezbătută în întâlnirile informale dintre profesori: mutarea lecţiei despre sisteme de ecuaţii 2X2 din finalul clasei a VII-a în finalul clasei a VIII-a. Am mai vorbit despre această temă, dar subiectul este prea grav ca să îl considerăm încheiat.
Pentru a înţelege fenomenul trebuie să aruncăm o privire în trecut. Cele două forme tradiţionale de rezolvare a sistemelor de ecuaţii sunt metoda substituţiei (a înlocuirii), o metodă mai “manufacturieră” ce prinde foarte bine la unii elevi mai slabi, şi metoda reducerii, o metodă mai “turbo”, cu atracţie mai ales la elevii buni. Tradiţional acestea se parcurgeau “la pachet”, dezvoltând în gândirea elevilor abilităţi de calcul absolut necesare în învăţarea algebrei. Acestea sunt nişte metode cu un grad puternic de naivitate şi, pe vremuri, ele erau stabilizate prin trecerea la sistemele de 3 ecuaţii cu 3 necunoscute, în care de multe ori se aplică în cadrul unei rezolvări ambele metode (vezi sistemele din culegerea lui Gheba). Pentru detalii vezi anexa din final.
Începând din anii ’80, lecţiei i-a fost adăugată o nouă metodă, cea grafică, metodă ce a primit întâietate la predare, fiind prima care apărea în viaţa elevilor. Este evident că accentul s-a mutat cu această ocazie spre zona mai riguroasă a funcţiilor, a geometriei analitice, prin prezentarea ecuaţiilor ca ecuaţii a unei drepte. Mişcarea a avut câteva urmări didactice pe care le voi discuta în continuare.
În primul rând, noua linie nu a putut fi continuată şi la sistemele 3×3, cu reprezentare grafică în spaţiul 3D (evident de ce!), motiv pentru care, cu timpul, acestea au fost eliminate din programă (abandonându-se după 1990). Când eram elevi, nouă ne plăceau foarte mult sistemele 3×3; aici erau adevăratele provocări, nu ca la cele plictisitoare de 2×2, şi este mare păcat că acestea au fost abandonate. În acest moment se naşte o nouă problemă, colaterală, de înţelegere a matematicii de către elevi: înseamnă că sistemele cu mai multe ecuaţii şi necunoscute se pot aborda doar prin metodele complicate din clasa a XI-a?! Se poate gândi astfel, nu-i aşa? (Apropos, prin anii ’90 într-o culegere renumită, existau două pagini înghesuite cu sisteme 2×2 la care toate dădeau răspunsul (1;1), în afară de un singur exerciţiu, care avea altă soluţie; dacă tocmai nu-l găseau pe acela, elevii puteau înţelege că orice sistem are soluţia x = 1 şi y = 1)
În al doilea rând, elevii înţeleg mult mai greu metoda grafică decât pe celelalte. Or, aceasta venind prima, impresia creată se extinde automat asupra întregii lecţii despre sisteme de ecuaţii (am făcut sisteme de ecuaţii, este o lecţie foarte grea!). Până la începutul anilor 2000, elevii fiind destul de docili, lecţia a rezistat în programa de a VII-a, după care a fost exilată la sfârşitul clasei a VIII-a în 2009, sub pretextul că lecţia este prea grea. Din păcate, lecţia a fost mutată tot în această ordine (metoda grafică înaintea celor tradiţionale), aşa că problema tot nu s-a rezolvat: prima impresie asupra elevilor este tot cea veche, că este o lecţie grea L.
Este evident că toată lumea suferă, dar mai ales elevii, care se trezesc brusc în cine-ştie-ce problemă cu o situaţie de sistem de ecuaţii, înainte de a face lecţia la clasă oficial.
Cum am rezolvat personal această situaţie problematică? Am mai prezentat-o, dar o reiau şi acum, anume prin mutarea lecţiei cu cele două metode tradiţionale la începutul clasei a VIII-a (forma naivă a lecţiei) şi parcurgerea separată a metodei grafice, ulterior, în cadrul capitolului despre funcţii (forma riguroasă a lecţiei, la o a doua tratare). Astfel, în cadrul primului capitol parcurg următoarele lecţii:
Lecţia 0: Ecuaţii cu două necunoscute, cărora le putem găsii oricâte soluţii (nu ne interesează aici reprezentarea grafică a acestora şi faptul că acestea sunt situate pe o dreaptă, ci rămânem la forma elementer algebrică, de exemplu x = 3 şi y = 5).
Lectia 1: Două ecuaţii cu două necunoscute prin metoda substituţiei (înlocuirii); ataşând unei ecuaţii de la lecţia precedentă o a doua ecuaţie, se obţine doar o soluţie bună pentru amândouă. Pentru ca elevii să se poată concentra toţi asupra lecţiei, le ofer doar exemple de sisteme în care măcar una din ecuaţii are una din necunoscute “fără coeficient” (cu coeficientul +1 sau –1), evitând astfel exprimarea acesteia printr-o fracţie care i-ar speria pe foarte mulţi elevi.
Lecţia 2: Două ecuaţii cu două necunoscute prin metoda reducerii; această metodă mult mai rapidă vine ca o salvare la sistemele unde metoda substituţiei ne-ar duce la calcule cu fracţii. Mulţi elevi observă asemănarea acestei metode cu amplificarea pentru aducere la acelaşi numitor la adunarea fracţiilor. Şi în cazul acestei metode trebuie lucrat crescător. Astfel, la primul exemplu dau un sistem unde reducerea se face “din prima”, nefiind necesară o amplificare prealabilă. Doar apoi apare amplificarea unei ecuaţii pentru a cauza reducerea., apoi amplificarea simultană a ambelor ecuaţii. În mod similar cu paşi de la adunarea fracţiilor, şi aici trebuie să creştem la amplificări tot mai complicate cu fiecare nou sistem oferit spre rezolvare.
Pentru început, ca o regulă grosieră la ambele metode, le ofer elevilor garanţia că le dau sisteme cu soluţii numere întregi (până prind schema de lucru). De-abia din orele următoare luăm şi cazuri la întâmplare, cu soluţii fracţionale. După lecţia 1 trebuie avertizaţi elevii că mai vine o metodă, dar să nu-i lase pe “cei de-acasă” să le strice surpriza, ci să lucreze doar pe metoda substituţiei. Un elev m-a avertizat la începutul lecţiei 2 că a aflat cum merge “şmecheria” mai simplu, aşa că am decis ca el să tacă în procesul de descoperire a metodei reducerii.
În lecţiile următoare parcurgem câteva sisteme de 3×3 (le plac foarte mult elevilor), cât şi probleme ce se rezolvă cu ajutorul sistemelor de ecuaţii. Trebuie precizat că în această fază de rezolvare, cel puţin la început, scriem soluţia algebric, de pildă x = 3 şi y = –1, eventual aranjate sub forma unui mic sistem. De-abia în semestrul II, după reprezentarea punctelor în plan, începem să scriem soluţiile ca mulţime de puncte. Iar când mă întreabă elevii, la sistemele 3×3 cum scriem soluţia ca punct, le arăt că o scriem ca punct 3D J.
O observaţie specială ar fi necesară aici în legătură cu alte metode elementare de rezolvare a sistemelor. De exemplu, în manuale din Germania am găsit multe sisteme de forma: x = 2y + 1 şi x = –y + 5, ce se rezolvă cel mai bine cu o metodă ce poate fi numită metoda tranzitivităţii, ducând direct la ecuaţia 2y + 1 = –y + 5. Este evident că această metodă este mult mai rapidă în cazul intersecţiei graficelor a două funcţii. Din păcate am întâlnit elevi care la acest sistem mai întâi mută toate necunoscutele în membrul stâng, după care rezolvă prin metodele tradiţionale.
Tot în manuale din Germania am găsit şi sisteme formate dintr-o ecuaţie cu două necunoscute şi o ecuaţie cu o necunoscută. Consider că acestea nu merită o atenţie prea mre; cel mult merită folosite ca trecere de la lecţia 0 la lecţia 1 sau, eventual, intercalate ca o banalitate, printre alte exerciţii.
ANEXĂ:
După ce am scris prezentul eseu, am luat la verificat “arhiva” personală. Permiteţi-mi să vă prezint ce am găsit despre programa şi manualele din anii ’70, respectiv ’80.
În anii ’70 sistemele de ecuaţii (2×2 şi 3×3) erau în cadrul capitolului despre ecuaţii din clasa a VIII-a. Precizez că la vremea respectivă toţi împlineam 14 ani în clasa a VIII-a (mergeam în clasa I cu şase ani şi făceam buletin la sfârşitul şcolii generale). Iată câteva exemple.
Programa de matematică pt. clasele V-X ale şcolii generale (Bucureşti 1972): Clasa a VIII-a, Cap. III, Ecuaţii de gradul I,
- Rezolvarea ecuaţiilor de gradul I cu coeficienţi numerici şi literari (recapitulare Cl. a VII-a) Sisteme de două (trei) ecuaţii de gradul I cu două (trei) necunoscute cu coeficienţi numerici şi literari. Rezolvarea problemelor cu ajutorul sistemelor de ecuaţii.
- Rezolvarea grafică a unui sistem de gradul I de două ecuaţii cu două necunoscute. Discuţia sistemului de două ecuaţii cu două necunoscute de gradul I, cu ajutorul graficului.
O situaţie similară, dar mai detaliată, se găseşte în Programa de matematică din 1977.
În manualul de Algebră pentru clasa a VIII-a (Ivanca Olivotto, Constantin Ionescu-Bujor, Ion Giurgiu, 1980), apar următoarele lecţii legate de subiectul eseului de faţă:
- Ecuaţii de gradul I cu două necunoscute
- Sisteme de ecuaţii de gradul I cu două necunoscute
- Rezolvarea sistemelor… Metoda substituţiei
- Rezolvarea sistemelor … Metoda reducerii
- Sisteme cu coeficienţi literari
- Sisteme de trei ecuaţii de gradul I cu trei necunoscute
- Probleme rezolvate cu ajutorul sistemelor de ecuaţii de gradul I
Analizând manualele din anii ’80-’90, găsim sistemele de ecuaţii cu un an mai devreme (ce-i drept, prin şcoli erau deja copii trimişi în clasa I la 7 ani, deci cu buletin în a 7-a). De pildă, în manualul de Algebră pentru clasa a VII-a (Tiberiu Spircu, Ioan Crăciunel, Lucia Chişu, 1989) avem următoarele lecţii:
- Ecuaţii de gradul I cu două necunoscute (unde apare dreapta soluţiilor reprezentată în sistemul cartezian de axe);
- Echivalenţa ecuaţiilor de gradul I cu două necunoscute;
- Noţiunea de sistem de ecuaţii (unde soluţia se găseşte la intersecţia celor două drepte ale ecuaţiilor, actala metodă grafică);
- Rezolvarea sistemelor prin metoda substituţiei;
- Sisteme echivalente;
- Metoda reducerii;
- Rezolvarea unor probleme cu ajutorul sistemelor de ecuaţii;
Sistemele 3×3 nu mai apar în acele manuale, dar profesorii le mai făceau la începutul anilor ‘90. Menţionez că în clasa a VIII-a studiam la vremea respectivă deja polinoame.
Titus Grigorovici
29 sept. 2016







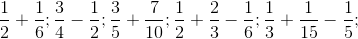 eventual
eventual 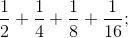 etc.
etc.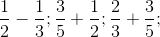 eventual, până la situaţii “extreme”
eventual, până la situaţii “extreme” 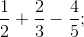 etc.
etc.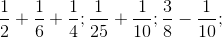 etc.
etc.