Numerele prime reprezintă atomii, părţile componente din care sunt create multiplicativ toate celelalte numere. A reduce aceste minuni matematice la o simplă şi unică definiţie este tot ce poate fi făcut mai rău minţii tinere şi proaspete a elevului de clasa a V-a. Acesta, doritor de a afla cât mai multe lucruri frumoase de la profesorul de matematică, este “lovit” cu o definiţie unilaterală, ce surprinde doar o singură faţetă a acestor nestemate matematice. În urma unei astfel de predări, cei mai mulţi nu ajung să le înţeleagă, se sperie de ele şi de orice apariţie a acestora, ca de nişte ciudate bestii cu care cel mai bine să nu ai de-a face; le asimilează deseori numerelor impare şi se blochează când le vorbeşti de 2 ca număr prim par sau de 9 sau de 15 ca numere impare neprime. Abordarea cunoaşterii intuitive din cât mai multe situaţii poate ajuta mult în prevenirea “ceţii ce se pune pe creierul” multor elevi în ceea ce priveşte numerele prime.
De mulţi ani încerc să găsesc diferite căi de a mă apropia de noţiunea de număr prim într-un mod cât mai natural, potrivit elevului de gimnaziu aflat în proces, undeva între gândirea aritmetică a ciclului primar şi gândirea matematică avansată ce va să vină cu înaintarea în vârstă. La clasa a V-a de anul acesta am reuşit încă un pas important în acest demers, găsind în sfârşit o explicaţie plauzibilă pentru denumirea acestor numere, lămurind astfel care este legătura între numerele prime şi cuvântul “primul”. Cu elevii de anul acesta am reuşit nu mai puţin de şase-şapte abordări mai mult sau mai puţin diferite a noţiunii de număr prim. Iată-le în continuare pe acestea în ordinea în care au apărut în lecţii, dar şi altele ce vor apărea la discuţii ulterioare.
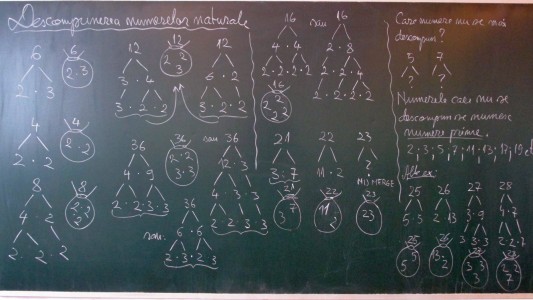
Pasul 1) Prima apariţie a numerelor prime a fost în cadrul unui “joc”, în care ne-am propus să descompunem multiplicativ diverse numere. Abordarea a fost una profund intuitivă, fără nici o cât de mică tentativă de teoretizare prealabilă: pur şi simplu, le-am arătat elevilor câteva exemple, pe marginea cărora am discutat principalele aspecte ale “jocului”: că numărul 1 nu participă pentru că atunci jocul nu s-ar mai termina, că pot exista diferite căi de a descompune un număr, dar că întotdeauna se ajunge la aceeaşi formă finală, descompunerile putând varia doar comutativ, că există numere la care descompunerea este mai stufoasă, mai bogată, dar şi numere mai sărace, iar aceasta nu depinde de mărimea numărului (ce ciudat!); în sfârşit, am constatat că există numere care nu se pot descompune multiplicativ. În acest moment au apărut aproape deodată primele două descrieri ale ideii de număr prim. Numerele din finalul oricărei descompuneri se numesc numere prime; ele sunt un fel de piese de bază din care sunt compuse multiplicativ toate celelalte numere, ca într-un ciudat joc Lego. Astfel, există piese mai mici, de 2, 3 sau 5 unităţi, sau piese mai mari de 7 sau 11 unităţi sau mai multe. Pe de altă parte, numerele prime apar la startul unor “partide”, acele numere la care avem surpriza să constatăm că nu le putem descompune în cadrul acestui “joc”. Da, există şi numere prime mai mari, cum ar fi 13, 17 sau 19. Aici apare prima oară o întrebare ciudată: “mai există şi alte astfel de numere, mai mari?”. După cât mai multe exemple rezolvate în clasă, ca temă, elevii au avut să descompună intuitiv şi restul numerelor până la 100 (cât mai multe; unii le-au descompus pe toate care se puteau, alţii au urcat doar către 50). La recapitularea de la începutul următoarei ore am concluzionat că există două tipuri de numere: numerele prime şi numerele compuse; numerele compuse sunt acelea care se pot descompune în produs, pe când numerele prime nu se pot descompune.
După acest prim contact cu numerele prime am încercat şi o primă listă de contabilizare a acestora, listă care, în funcţie de elev, arăta cam aşa: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, etc. Aspectul comutativităţii înmulţirii numerelor naturale a apărut aici din belşug, şi reprezintă unul din gândurile de unde mi-a venit ideea de a aduna piesele componente ale fiecărui număr descompus într-un săculeţ (adică numerele prime), săculeţ în care acestea se amestecă, necontând la produsul final ordinea în care se reînmulţesc. Lecţiile şi-au urmat apoi cursul către introducerea formei oficiale a descompunerii numerelor naturale, binecunoscuta descompunere “cu bară”. Cuprinse doar pe baza celor înţelese intuitiv la prima lecţie despre descompunerea numerelor naturale, numerele prime au apărut în fiecare din lecţiile următoare, prin simpla folosire tot mai frecventă, chiar dacă noţiunea nu era încă lămurită complet din punct de vedere oficial. De pildă, cu timpul s-a ajuns fără nici un stres la folosirea naturală a expresiei “descompunerea în produs de puteri de factori primi”.
Pasul 1’) Un mic pas înainte, care ţine totuşi de aspectul de descompunere în produs a unui număr, l-am făcut atunci când am încercat un alt “joc”. Astfel, ne-am propus să reprezentăm diferite numere naturale cu punctuleţe în formă dreptunghiulară. Aceste reprezentări pot fi făcute cu punctuleţe aliniate pe hârtie sau cu punctuleţe materiale ordonate pe masă (monede de un ban, boabe de cafea sau de fasole). Ideea apare exploatată din belşug în romanul lui Apostolos Doxiadis – Unchiul Petros şi Conjectura lui Goldbach (Ed. HUMANITAS, 2003) Astfel, la pagina 120, numerele compuse sunt prezentate în formă dreptunghiulară de rânduri şi coloane. De exemplu, numărul 35 are o singură reprezentare posibilă, de 5 rânduri şi 7 coloane, care poate fi însă comutată în 7 rânduri şi 5 coloane (comutativitatea reprezentată vizual). Numărul 24 are trei reprezentări total diferite: 4 ∙ 6, 3 ∙ 8 şi 2 ∙ 12. La unele numere reprezentarea în formă dreptunghiulară apare în forma unui pătrat. Astfel, la numărul 16 avem reprezentarea dreptunghiulară 2 ∙ 8 şi reprezentarea pătrată 4 ∙ 4. Întorcându-ne la tema noastră, observăm că numerele prime nu pot fi reprezentate sub formă de dreptunghiuri complete. În romanul lui Apostolos Doxiadis, Unchiul Petros le reprezenta sub forma unor şiruri de punctuleţe de un rând.
Pasul 2) O nouă apropiere de numerele prime am avut odată cu studierea unor şiruri elementare de numere. Elevii din şcolile Waldorf folosesc din ciclul primar expresii de genul şirul lui 3, cu sensul de şirul multiplilor lui 3, înţelegând prin acestea rezultatele tablei înmulţirii. Aşadar, fără mari complicaţii teoretice, doar intuitiv, am putut enumera câteva şiruri de multipli (multipli = un număr de mai multe ori, clar), pornind de la numărul însuşi. Este foarte important să ne înfrânăm aici să “recităm” lecţia teoretică şi riguros completă (impuls dominant la majoritatea profesorilor), pentru că numărul zero, prezentat de obicei ca primul multiplu, doar încurcă aici lucrurile. Oricum, demersul în această formă este profund corect din punct de vedere istoric: numărul zero a apărut mult mai târziu decât numerele prime. Ca urmare, pe tablă am scris ceva de genul:
M2: 2, 4, 6, 8, 10, 12, 14, …
M3: 3, 6, 9, 12, 15, 18, 21, …
M4: 4, 8, 12, 16, 20, 24, …
M5: 5, 10, 15, 20, 25, 30, …
M6: 6, 12, 18, 24, 30, 36, …
M7: 7, 14, 21, 28, 35, 42, …
M8: 8, 16, 24, 32, 40, 48, …
M9: 9, 18, 27, 36, 45, 54, …
Observăm că numerele 4, 6, 8, 9 etc. apar în diverse şiruri de multipli, pe diferite poziţii. Dimpotrivă, numerele 2, 3, 5, 7 etc. apar în aceste şiruri doar pe prima poziţie; de aia ele se numesc numere prime. Într-adevăr, acestea se numesc numere prime pentru că apar în şirurile de multipli doar pe prima poziţie! Cu această ocazie am aflat deci, de ce se numesc aşa. În alte limbi, cum ar fi germana, nu pot fi făcute astfel de conexiuni; cu atât mai păcat este să ratăm o ocazie ce ne-o oferă “pe tavă” limba noastră.
Această mişcare a fost posibilă pentru că am înlocuit în limbajul folosit noţiunea de multiplu în sens riguros teoretic cu noţiunea de multiplu în sens istoric. Mai putem face un pas în acest proces şi să analizăm cum stau lucrurile dacă apelăm şi la noţiunea de multiplu în sens lingvistic: multiplii unui număr reprezintă numărul luat de mai multe ori (multiplu = de mai multe ori); multiplul unui număr subînţelege că acel număr este la plural, nu la singular, adică nu este luat doar o singură dată. Aceasta este de fapt cea mai naturală formă de a vorbi despre multipli.
De aici apare Ciurul lui Eratostene, o lecţie foarte practică, din păcate de mult abandonată de învăţământul nostru vitezoman, ce nu-şi mai găseşte timp pentru astfel de fleacuri. În Ciurul lui Eratostene exact asta se întâmplă: încercuim primul număr după 1, adică pe 2 (pe 1 de mult l-am exclus din aceste jocuri, deci copiii n-au nici o problemă în a începe de la 2) şi apoi tăiem toţi multiplii lui 2 – toţi multipli în sens lingvistic; acum primul număr rămas netăiat este 3; îl încercuim pe 3 şi tăiem apoi toţi multiplii săi – toţi multiplii în sens lingvistic, şi aşa mai departe cu următoarele numere prime.. Astfel, în Ciurul lui Eratostene apare o altă faţetă a multiplei personalităţi a numerelor prime, anume că numerele prime reprezintă numerele rămase în Ciurul lui Eratostene după ce tăiem toţi multiplii (toţi multiplii în sens lingvistic).
Acest aspect iese foarte bine în evidenţă dacă faceţi Ciurul lui Eratostene până la 250 (ştiu, nu-i uşor). După lunga muncă de rutină de încercuit un număr prim şi tăiat toţi multiplii săi, până la 11 şi multiplii săi, care sunt încă uşor de găsit, la 13 apare întrebarea dacă mai sunt multipli de-ai săi încă netăiaţi. Aici îi confrunt pe elevi cu o întrebare ajutătoare: “care a fost primul număr tăiat la şirul lui 5? Sau la şirul lui 7?”. După o scurtă dezbatere elevii observă că este vorba de pătratul numărului prim la care tocmai lucram. Când l-am încercuit pe 5 ca prim, mulţi din multiplii săi erau deja tăiaţi de la şirul lui 2 sau de la şirul lui 3. Primul care nu era tăiat şi l-am tăiat proaspăt era 25. La fel, primul multiplu tăiat doar la şirul lui 7 a fost 49. O verificare scurtă şi la 11 ne convinge: la şirul multiplilor lui 13 nu mai trebuie să verificăm, primul ce încă n-a fost eliminat este 169. În continuare mai găsim de tăiat doi multipli de-ai lui 13, pe 13 ∙ 17 = 221 şi pe 13 ∙ 19 = 247. Acum trecem la următorul număr prim, la 17. Care este primul multiplu al lui 17 ce încă nu este eliminat din Ciurul lui Eratostene? Clar, este 172 = 289, dar care este deja în afara limitei ce ne-am propus-o. Înseamnă că toate numerele rămase încă netăiate sunt numere prime (observaţie valabilă în lista numerelor până la 250). Acum se înţelege desigur că dacă vrei să faci la clasă Ciurul lui Eratostene cu copiii, fiecare în caietul lui, îţi ocupă din plin o oră.
Câteva precizări metodice merită făcute, legat de această lecţie. Eu m-am străduit să scriu cât mai mic, pentru ca să-mi încapă 25 de rânduri pe înălţimea de 1,10 m a tablei. Elevii trebuiau să înceapă o pagină nouă, pe lângă titlul – care pe tablă era alături – având întreaga pagină la dispoziţie. Oricum, trebuie atenţionaţi să copieze tabelul exact ca pe tablă, pentru a avea o ordine în care să se descurce (unii totuşi tot nu reuşesc). Pentru o ordine cât mai clară, eu îl scriu pe 1 la început, iar apoi îl şterg când începem munca la ciur. Desigur că, după completarea tabelului, luăm o scurtă pauză în care le povestesc ce este acela un ciur pentru sortat pietrişul pe diferite mărimi.
Apoi, aşa cum se vede şi în poza de final a tablei, la primele “site” ale ciurului folosesc la fiecare câte o culoare diferită; de-abia de la 13 nu mai schimb culoarea cretei pentru restul numerelor prime găsite. Ora următoare aruncăm o privire înapoi în care scriem întâi lista numerelor prime cel puţin până la 100 (anul acesta elevii au vrut să mergem mult mai mult), ordonate de data asta pe coloane: prima coloană cele de o cifră, a doua coloană cele între 10 şi 20 (câte patru pe fiecare coloană), apoi cele două dintre 20 şi 30 (două numere prime), pe a patra coloană cele între 30 şi 40, apoi cele între 40 şi 50 (trei numere prime) ş.a.m.d. Apoi facem o analiză cu tot ce-am observat. De pildă că într-o decadă pot fi cel mult patru numere prime (la primele două coloane, dar şi mai târziu, de exemplu între 190 şi 200), dar şi că există decade fără numere prime ( am avut una între 200 şi 210).
Ca o curiozitate le povestesc şi despre numerele prime gemene (numere prime despărţite doar de numărul par dintre ele), despre felul în care acestea sunt scrise, de pildă 26∙3±1 pentru 191 şi 193, dar şi scurt, superficial, despre faptul că numerele prime gemene foarte mari, încă necunoscute pentru restul lumii, sunt folosite la codificarea mesajelor secrete pe internet.
Pasul 3) O nouă sesiune de întâlniri cu numerele prime apare desigur atinci când începem să discutăm despre divizorii unui număr. Aici, în sfârşit, lucrurile ajung “în ape cunoscute” pentru majoritatea părinţilor, care au trebuit să îndure cu stoicism o materie necunoscută lor, materie care nu prea semăna cu definiţia ce o ţineau ei minte din liceu. Aici discutăm despre divizori propri şi divizori impropri şi putem spune în sfârşit că numerele prime sunt acele numere care se divid doar la unu şi la el însuşi, sau, cu alte cuvinte, că numerele prime sunt numerele care au doar divizori impropri. Spre deosebire de acestea, numerele compuse au întotdeauna şi cel puţin încă un divizor propriu în plus. Merită aici să vă prezint o definiţie găsită într-o veche carte germană (G. Ulrich, Arithmetik und Algebra, 1940): numărul prim este un număr care nu este divizibil prin nici un alt număr (în afară de 1). Această descriere elimină foarte abil divizorul numărul însuşi, prin forma exprimării (nu este divizibil prin nici un alt număr).
Artificiul de exprimare îmi aduce aminte de felul cum poţi ridica la pătrat un număr cu un calculator de buzunar. De pildă, pentru 172 trebuie să apăsăm 17 x = şi obţinem instant 289, pentru că gândirea calculatorului înmulţeşte număr iniţal cu numărul de pe ecran, odată ce ai apăsat semnul egal.
Înainte de a încheia acest eseu “filozofic” despre numerele prime, îmi permit două ultime reveniri scurte la subiectul multiplilor unui număr (acestea au fost doar parţial prezentate elevilor). În primul rând, ne aducem aminte că la divizorii unui număr natural avem întotdeauna, sigur cel puţin doi divizori*, anume numărul 1 ca divizor universal, şi numărul însuşi, cele două numere purtând numele de divizori impropri; ceilalţi divizori se numesc divizori propri. În mod analog putem privi lucrurile şi la multiplii unui număr: orice număr îl are pe 0 (zero) ca multiplu universal şi pe numărul însuşi ca multiplu, cei doi multipli putând fi denumiţi în mod similar multipli impropri. Ceilalţi multipli, pe care i-am caracterizat mai devreme ca “plurali”, vor putea fi numiţi în mod similar drept multipli propri. Astfel (după ce am eliminat cei “doi ciudaţi”, 0 şi 1) numerele prime sunt numerele rămase după excluderea tuturor multiplilor propri din lista numerelor naturale. (* în afara cazului numărului 1, care are doar un divizor; aici găsim încă o explicaţie pentru care numărul 1 nu este considerat prim: numerele prime sunt acele numere care au exact doi divizori)
A doua revenire legată de multiplii se referă la expresia folosită de multiplu în sens lingvistic (fără zero şi numărul însuşi, adică multiplu drept un “plural”) spre deosebire de multiplu în sens riguros teoretic (varianta folosită actualmente şi şcoli) sau varianta intermediară de multiplu în sens istoric (doar fără zero, care nu era cunoscut în antichitate). Am discutat cu un expert lingvist, care mi-a sugerat termenul de multiplu în sensul uzanţei generale, folosit de toată lumea, pentru multiplul plural (adică fără 0 şi 1), respectiv multiplu în sens restrâns, folosit doar de către matematicieni (pentru toţi multiplii în sens ştiinţific). Acest punct de vedere se aseamănă cu situaţia greutăţii (termen folosit în sens larg de către toată lumea), respectiv a masei (termenul ştiinţific corect pentru mărimea măsurată în kg, dar folosit în cerc restrâns, doar în lumea ştiinţifică a fizicii şi a domenilor conexe).
28 Dec. 2016
Titus Grigorovici