Dacă tot am deschis tolba cu zaruri ciudate, ce ziceţi de nişte zaruri care nici măcar nu mai sunt cubice? Da, există şi aşa ceva, iar cei mai buni candidaţi la astfel de zaruri sunt desigur corpurile perfecte cu mai multe feţe decât şase, aşa-numitele corpuri platonice. Să le luăm la rând: în prima imagine vedeţi un octaedru regulat – cel negru – cu feţe de la 1 la 8, dar şi un decaedru semiregulat – cel muştăriu – cu feţele numerotate de la 0 la 9.
Următoarea imagine prezintă zaruri dodecaedre, cu 12 feţe pentagoane regulate numerotate de la 1 la 12. Cel din stânga este un astfel de zar simplu, pe când cel din dreapta este un dublu dodecaedru cu unul mic în interiorul celui mare. Acestea sunt foarte bune la elevii mici: arunci o dată, iar ei trebuie să facă în minte operaţia cerută cu cele două numere.
Desigur că se pot realiza şi zaruri pe icosaedre, corpuri regulate cu 20 feţe triunghiuri echilaterale. Putem arunca cu două zaruri, sau putem alege icosaedrul dublu; oricum, sarcina de a face în cap adunarea celor două numere este ceva mai dificilă. La fel şi când se doreşte exersarea scăderii sau a înmulţirii. Colegele noastre învăţătoare folosesc mult aceste zaruri în perioada de stabilizare a învăţării operaţiilor. Zarurile icosaedre pot fi folosite la încălzirea minţii şi la clasa a V-a; nu-i uşor să înmulţeşti în cap 17 cu 8, sau 12 cu 15 etc.
Este de la sine înţeles că vom căuta şi la acestea ceva similar cu proprietatea de 7 de la zarurile normale. Elevii deştepţi o intuiesc imediat atunci când le pun un astfel de zar în faţă pe masă şi îi întreb ce număr este dedesupt?. Imediat le luceşte privirea şi îşi adaptează vechile cunoştinţe la noua situaţie. Da, elevii găsesc imediat regula de 13 la dodecaedru, respectiv faptul că la icosaedru suma a două feţe opuse este întotdeauna 21.
Din păcate, astfel de zaruri nu se găsesc în magazinele noastre. Nici în străinatate nu pot fi achiziţionate de oriunde. Zarurile noastre sunt cumpărate din magazinele unor muzee din Germania (Muzeul jucăriilor din Nürenberg, respectiv Deutsches Museum din München). În Cluj am găsit totuşi următoarele două zaruri icosaedre. Acestea nu au însă feţele numerotate respectând regula ca suma feţelor opuse să fie constantă. La acestea feţele sunt numerotate pentru a putea ţine un scor la un joc; astfel de la orice număr se poate trece la numărul următor pe faţa vecină printr-o simplă răsturnare a zarului. Ultima dată am întâlnit un zar pe dodecaedru în vară,la un joc oferit de reţeaua de magazine Lidl, dar acesta avea fiecare număr de la 1 la 6 de câte două ori, folosind doar facptul că dodecaedrul se rostogoleşte foarte uşor şi are o asemănare interesantă cu mingea de fotbal.
Tolba cu zaruri

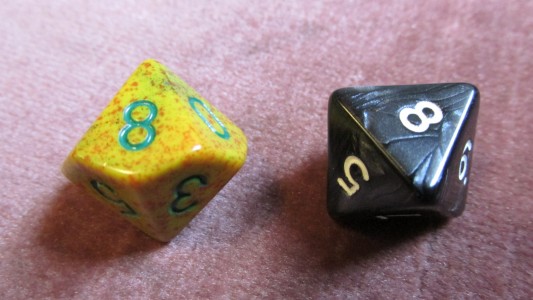



V`as putea recomanda un magazin in Iasi de unde puteti cumpara astfel de zaruri.