Category: Metodică

Exemplul 7: Adunarea fracţiilor

Exemplul 8: Sisteme de ecuaţii

Despre subiectul matematicii naive cred că am spus destul de multe încât să se înţeleagă despre ce este vorba. Totuşi, revin cu încă o tură de exemple, datorită unui comentariu din data de 02.06.2016, făcut de către un domn profesor pe site-ul didactic.ro la zona de dezbatere a noilor programe. Dânsul zice acolo: Eu cred ca scoaterea c.m.m.m.c. de la clasa a V-a. Aflarea numitorului comun prin ghiciri şi încercări, pentru a putea aduna două fracţii, nu mai seamănă a matematică.

Aici este evidentă neînţelegerea la nivelul profesorilor a adaptării predării la nivelul vârstei, cauzată de faptul că “programă din 2009” nu a fost însoţită şi de indicaţii metodico-didactice în care să se explice “noua linie de predare”. Iată cum am înţeles eu predarea la adunarea fracţiilor în contextul acestui subiect şi al acestei programe (când mă refer la adunare, subînţeleg desigur şi scăderea).

Într-o primă etapă, în clasa a IV-a, elevii învaţă cu doamnele învăţătoare adunarea fracţiilor cu acelaşi numitor (pe germană se spune gleichnamig, adică cele cu acelaşi nume). În a doua etapă, în clasa a V-a, se aduc fracţiile la acelaşi numitor în mod intuitiv, în forme de la simplu la tot mai complicate. În final, pentru cazurile cele mai dificile, unde intuiţia nu mai face faţă, parcurgem în clasa a VI-a găsirea c.m.m.m.c., cu care aflăm numitorul comun în format “automatizat”.

Este clar că, în comentariul de pe didactic.ro, e vorba despre etapa a doua. În această etapă elevii nu găsesc numitorul comun prin ghiciri şi încercări, ci prin pură înţelegere matematică intuitivă a numerelor, a fenomenului fracţiilor, aplicând proaspăt învăţata amplificare. Problema este însă, cum privim copilul? Îl privim ca pe un sac gol în care noi, profesorii trebuie să turnăm cunoştinţe, sau îl privim ca pe un om care gândeşte singur şi noi trebuie doar prin natura sarcinilor şi a provocărilor să-i cauzăm, să-i pornim gândirea? Îi dăm noi cunoştinţele respective, sau îl ajutăm pe el să le genereze? Îi dăm în fiecare zi un peşte, sau îl învăţăm să pescuiască? Aici am ajuns din nou la opoziţia dintre matematica rezultat, oferită elevului sub forma unei scurte prelegeri (la adunarea fracţiilor se procedează astfel: …), pe de-o parte, şi matematica proces, în care elevul este atras să o descopere singur prin problematizare (oare ce-ar trebui să face aici ca să putem aduna aceste fracţii?), pe de cealaltă parte.

Sigur, aici ajută un pic de explicaţii grafice: de pildă, a reprezenta o jumătate sub forma unui semidisc care, împărţit în trei părţi egale, arată cum se ajunge la 3/6. Alegerea primelor exemple este însă determinantă în procesul de înţelegere al elevilor. În acest sens eu practic o predare prin descoperire, în care elevii găsesc singuri cum să rezolve exerciţiile propuse, în timp ce eu ridic treptat ştacheta dificultăţii. Iată o posibilitate de ordonare a primelor exerciţii pe nivele de modele:

Modelul 0: recapitulare din clasa a IV-a;

Modelul 1: 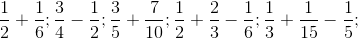eventual  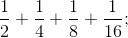etc.

Modelul 2: 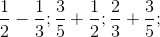eventual, până la situaţii “extreme”  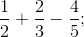etc.

Modelul 3: 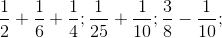etc.

Probabil că la primul exerciţiu de la modelul 1 trebuie ajutată clasa s[ facă primul pas, “traducând” elevilor împărţirea de mai sus a jumătăţii în trei şesimi, într-o amplificare. La următoarele elevii intră în joc imediat şi ştiu ce să facă în continuare.

La modelul 3 se poate urca atâta cât “duc” elevii, oricum rămânănd în zona de numere accesibile calculului în cap. Pe această cale, elevii învaţă adunarea/ scăderea fracţiilor ca fenomen în clasa a V-a pe exemple accesibile, urmând ca formele complicate, cazurile grele, să le parcurgă în clasa a VI-a, după învăţarea găsirii c.m.m.m.c. prin reţeta oficială. Astfel, cunoaştem fenomenul în forma sa naivă, apoi îl aprofundăm în forma riguroasă la o a doua trecere (predarea în spirală).

Revenirea la subiectul matematicii naive, pe exemplul adunării fracţiilor din clasa a V-a, această revenire îmi oferă ocazia de a aborda încă o temă mult dezbătută în întâlnirile informale dintre profesori: mutarea lecţiei despre sisteme de ecuaţii 2X2 din finalul clasei a VII-a în finalul clasei a VIII-a. Am mai vorbit despre această temă, dar subiectul este prea grav ca să îl considerăm încheiat.

Pentru a înţelege fenomenul trebuie să aruncăm o privire în trecut. Cele două forme tradiţionale de rezolvare a sistemelor de ecuaţii sunt metoda substituţiei (a înlocuirii), o metodă mai “manufacturieră” ce prinde foarte bine la unii elevi mai slabi, şi metoda reducerii, o metodă mai “turbo”, cu atracţie mai ales la elevii buni. Tradiţional acestea se parcurgeau “la pachet”, dezvoltând în gândirea elevilor abilităţi de calcul absolut necesare în învăţarea algebrei. Acestea sunt nişte metode cu un grad puternic de naivitate şi, pe vremuri, ele erau stabilizate prin trecerea la sistemele de 3 ecuaţii cu 3 necunoscute, în care de multe ori se aplică în cadrul unei rezolvări ambele metode (vezi sistemele din culegerea lui Gheba). Pentru detalii vezi anexa din final.

Începând din anii ’80, lecţiei i-a fost adăugată o nouă metodă, cea grafică, metodă ce a primit întâietate la predare, fiind prima care apărea în viaţa elevilor. Este evident că accentul s-a mutat cu această ocazie spre zona mai riguroasă a funcţiilor, a geometriei analitice, prin prezentarea ecuaţiilor ca ecuaţii a unei drepte. Mişcarea a avut câteva urmări didactice pe care le voi discuta în continuare.

În primul rând, noua linie nu a putut fi continuată şi la sistemele 3×3, cu reprezentare grafică în spaţiul 3D (evident de ce!), motiv pentru care, cu timpul, acestea au fost eliminate din programă (abandonându-se după 1990). Când eram elevi, nouă ne plăceau foarte mult sistemele 3×3; aici erau adevăratele provocări, nu ca la cele plictisitoare de 2×2, şi este mare păcat că acestea au fost abandonate. În acest moment se naşte o nouă problemă, colaterală, de înţelegere a matematicii de către elevi: înseamnă că sistemele cu mai multe ecuaţii şi necunoscute se pot aborda doar prin metodele complicate din clasa a XI-a?! Se poate gândi astfel, nu-i aşa? (Apropos, prin anii ’90 într-o culegere renumită, existau două pagini înghesuite cu sisteme 2×2 la care toate dădeau răspunsul (1;1), în afară de un singur exerciţiu, care avea altă soluţie; dacă tocmai nu-l găseau pe acela, elevii puteau înţelege că orice sistem are soluţia x = 1 şi y = 1)

În al doilea rând, elevii înţeleg mult mai greu metoda grafică decât pe celelalte. Or, aceasta venind prima, impresia creată se extinde automat asupra întregii lecţii despre sisteme de ecuaţii (am făcut sisteme de ecuaţii, este o lecţie foarte grea!). Până la începutul anilor 2000, elevii fiind destul de docili, lecţia a rezistat în programa de a VII-a, după care a fost exilată la sfârşitul clasei a VIII-a în 2009, sub pretextul că lecţia este prea grea. Din păcate, lecţia a fost mutată tot în această ordine (metoda grafică înaintea celor tradiţionale), aşa că problema tot nu s-a rezolvat: prima impresie asupra elevilor este tot cea veche, că este o lecţie grea L.

Este evident că toată lumea suferă, dar mai ales elevii, care se trezesc brusc în cine-ştie-ce problemă cu o situaţie de sistem de ecuaţii, înainte de a face lecţia la clasă oficial.

Cum am rezolvat personal această situaţie problematică? Am mai prezentat-o, dar o reiau şi acum, anume prin mutarea lecţiei cu cele două metode tradiţionale la începutul clasei a VIII-a (forma naivă a lecţiei) şi parcurgerea separată a metodei grafice, ulterior, în cadrul capitolului despre funcţii (forma riguroasă a lecţiei, la o a doua tratare). Astfel, în cadrul primului capitol parcurg următoarele lecţii:

Lecţia 0: Ecuaţii cu două necunoscute, cărora le putem găsii oricâte soluţii (nu ne interesează aici reprezentarea grafică a acestora şi faptul că acestea sunt situate pe o dreaptă, ci rămânem la forma elementer algebrică, de exemplu x = 3 şi y = 5).

Lectia 1: Două ecuaţii cu două necunoscute prin metoda substituţiei (înlocuirii); ataşând unei ecuaţii de la lecţia precedentă o a doua ecuaţie, se obţine doar o soluţie bună pentru amândouă. Pentru ca elevii să se poată concentra toţi asupra lecţiei, le ofer doar exemple de sisteme în care măcar una din ecuaţii are una din necunoscute “fără coeficient” (cu coeficientul +1 sau –1), evitând astfel exprimarea acesteia printr-o fracţie care i-ar speria pe foarte mulţi elevi.

Lecţia 2: Două ecuaţii cu două necunoscute prin metoda reducerii; această metodă mult mai rapidă vine ca o salvare la sistemele unde metoda substituţiei ne-ar duce la calcule cu fracţii. Mulţi elevi observă asemănarea acestei metode cu amplificarea pentru aducere la acelaşi numitor la adunarea fracţiilor. Şi în cazul acestei metode trebuie lucrat crescător. Astfel, la primul exemplu dau un sistem unde reducerea se face “din prima”, nefiind necesară o amplificare prealabilă. Doar apoi apare amplificarea unei ecuaţii pentru a cauza reducerea., apoi amplificarea simultană a ambelor ecuaţii. În mod similar cu paşi de la adunarea fracţiilor, şi aici trebuie să creştem la amplificări tot mai complicate cu fiecare nou sistem oferit spre rezolvare.

Pentru început, ca o regulă grosieră la ambele metode, le ofer elevilor garanţia că le dau sisteme cu soluţii numere întregi (până prind schema de lucru). De-abia din orele următoare luăm şi cazuri la întâmplare, cu soluţii fracţionale. După lecţia 1 trebuie avertizaţi elevii că mai vine o metodă, dar să nu-i lase pe “cei de-acasă” să le strice surpriza, ci să lucreze doar pe metoda substituţiei. Un elev m-a avertizat la începutul lecţiei 2 că a aflat cum merge “şmecheria” mai simplu, aşa că am decis ca el să tacă în procesul de descoperire a metodei reducerii.

În lecţiile următoare parcurgem câteva sisteme de 3×3 (le plac foarte mult elevilor), cât şi probleme ce se rezolvă cu ajutorul sistemelor de ecuaţii. Trebuie precizat că în această fază de rezolvare, cel puţin la început, scriem soluţia algebric, de pildă x = 3 şi y = –1, eventual aranjate sub forma unui mic sistem. De-abia în semestrul II, după reprezentarea punctelor în plan, începem să scriem soluţiile ca mulţime de puncte. Iar când mă întreabă elevii, la sistemele 3×3 cum scriem soluţia ca punct, le arăt că o scriem ca punct 3D J.

O observaţie specială ar fi necesară aici în legătură cu alte metode elementare de rezolvare a sistemelor. De exemplu, în manuale din Germania am găsit multe sisteme de forma: x = 2y + 1 şi x = –y + 5, ce se rezolvă cel mai bine cu o metodă ce poate fi numită metoda tranzitivităţii, ducând direct la ecuaţia 2y + 1 = –y + 5. Este evident că această metodă este mult mai rapidă în cazul intersecţiei graficelor a două funcţii. Din păcate am întâlnit elevi care la acest sistem mai întâi mută toate necunoscutele în membrul stâng, după care rezolvă prin metodele tradiţionale.

Tot în manuale din Germania am găsit şi sisteme formate dintr-o ecuaţie cu două necunoscute şi o ecuaţie cu o necunoscută. Consider că acestea nu merită o atenţie prea mre; cel mult merită folosite ca trecere de la lecţia 0 la lecţia 1 sau, eventual, intercalate ca o banalitate, printre alte exerciţii.

ANEXĂ:

După ce am scris prezentul eseu, am luat la verificat “arhiva” personală. Permiteţi-mi să vă prezint ce am găsit despre programa şi manualele din anii ’70, respectiv ’80.

În anii ’70 sistemele de ecuaţii (2×2 şi 3×3) erau în cadrul capitolului despre ecuaţii din clasa a VIII-a. Precizez că la vremea respectivă toţi împlineam 14 ani în clasa a VIII-a (mergeam în clasa I cu şase ani şi făceam buletin la sfârşitul şcolii generale). Iată câteva exemple.

Programa de matematică pt. clasele V-X ale şcolii generale (Bucureşti 1972): Clasa a VIII-a, Cap. III, Ecuaţii de gradul I,

1. Rezolvarea ecuaţiilor de gradul I cu coeficienţi numerici şi literari (recapitulare Cl. a VII-a) Sisteme de două (trei) ecuaţii de gradul I cu două (trei) necunoscute cu coeficienţi numerici şi literari. Rezolvarea problemelor cu ajutorul sistemelor de ecuaţii.
2. Rezolvarea grafică a unui sistem de gradul I de două ecuaţii cu două necunoscute. Discuţia sistemului de două ecuaţii cu două necunoscute de gradul I, cu ajutorul graficului.

O situaţie similară, dar mai detaliată, se găseşte în Programa de matematică din 1977.

În manualul de Algebră pentru clasa a VIII-a (Ivanca Olivotto, Constantin Ionescu-Bujor, Ion Giurgiu, 1980), apar următoarele lecţii legate de subiectul eseului de faţă:

4. Ecuaţii de gradul I cu două necunoscute
5. Sisteme de ecuaţii de gradul I cu două necunoscute
6. Rezolvarea sistemelor… Metoda substituţiei
7. Rezolvarea sistemelor … Metoda reducerii
8. Sisteme cu coeficienţi literari
9. Sisteme de trei ecuaţii de gradul I cu trei necunoscute
10. Probleme rezolvate cu ajutorul sistemelor de ecuaţii de gradul I

Analizând manualele din anii ’80-’90, găsim sistemele de ecuaţii cu un an mai devreme (ce-i drept, prin şcoli erau deja copii trimişi în clasa I la 7 ani, deci cu buletin în a 7-a). De pildă, în manualul de Algebră pentru clasa a VII-a (Tiberiu Spircu, Ioan Crăciunel, Lucia Chişu, 1989) avem următoarele lecţii:

45. Ecuaţii de gradul I cu două necunoscute (unde apare dreapta soluţiilor reprezentată în sistemul cartezian de axe);
46. Echivalenţa ecuaţiilor de gradul I cu două necunoscute;
47. Noţiunea de sistem de ecuaţii (unde soluţia se găseşte la intersecţia celor două drepte ale ecuaţiilor, actala metodă grafică);
48. Rezolvarea sistemelor prin metoda substituţiei;
49. Sisteme echivalente;
50. Metoda reducerii;
51. Rezolvarea unor probleme cu ajutorul sistemelor de ecuaţii;

Sistemele 3×3 nu mai apar în acele manuale, dar profesorii le mai făceau la începutul anilor ‘90. Menţionez că în clasa a VIII-a studiam la vremea respectivă deja polinoame.

Titus Grigorovici

29 sept. 2016

MATEMATICA NAIVĂ

Exemplul 5: NUMERE COMPLEXE

Exemplul 6: COMBINATORICĂ

Plecând de la denumirea de matematică naivă, am putea uşor crede că aceasta se aplică doar elevilor mici, celor de gimnaziu, pe când “noi, în liceu, facem treabă serioasă”. Nimic mai greşit. Desigur că în liceu avem în faţa noastră elevi ce au fost deja selectaţi şi au făcut dovada că “pot duce mai multă matematică”. Dar, “mai multă matematică” nu înseamnă să-i îneci într-o matematică mult prea înaltă, prezentată după modelul universitar, doar pe baza faptului că vârfurile clasei chiar fac faţă (deseori doar aparent fac faţă, pentru că de multe ori există acolo un ajutor constant privat). Am explicat deja că matematica naivă nu ţine doar de primii paşi în matematică – adică la clasele mici –, ci ţine în general de primii paşi într-un domeniu nou al matematicii. Matematica se scutură încet, încet de naivitatea sa la următoarele abordări, la următoarele treceri prin subiectele respective. Astfel, temele de studiu ce apar pentru prima dată în liceu – adică majoritatea – trebuie prezentate fără discuţie la un nivel serios de naivitate, corespunzătoare unei prime abordări a subiectului nou. Primii paşi sunt extrem de importanţi: elevul trebuie să apuce în primul rând să înţeleagă de unde a apărut noua temă, iar aceasta nu apare din voinţa, din definiţia dată de un profesor atotputernic, care se crede Dumnezeu în lumea matematică a acelui elev.

De pildă, chiar şi ultimul elev dintr-o clasă de real trebuie să priceapă de unde apar numerele complexe! Acestea nu răsar din senin. Abordarea introdusă la reforma din 1980, de tipul “considerăm perechile ordonate (a;b), cu a,b∈ℝ cărora le definim următoarele operaţii….; acestea se numesc numere complexe; mulţimea numerelor complexe se notează cu ℂ ”, această abordare este percepută de majoritatea covârşitoare a elevilor ca inumană, extraterestră, total de neînţeles! Toţi elevii care vor să înveţe, odată ajunşi acasă după această lecţie, cer ajutorul cuiva să afle despre ce este vorba. Iar acesta (de obicei profesorul din particular) îi va povesti elevului imediat despre numărul i ca o convenţie pentru absurda rădăcină pătrată a lui –1, iar apoi imediat îi va arăta cum se aplică această nouă şmecherie la soluţiile nereale ale ecuaţiei de gradul II.  Este probabil exemplul cel mai reprezentativ în care o abordare cu un anume grad de naivitate va lumina instant faţa şi mintea  elevilor.

Pentru orice profesor cu o empatie funcţională faţă de mintea elevilor este clar că introducerea numerelor complexe axiomatic, definindu-le ca perechi ordonate de numere reale, cu operaţiile anexate, este total abstractă şi nepotrivită din punct de vedere pedagogic. Definirea înmulţirii a două astfel de perechi, (a; b)∙(c; d) = (ac–bd; ad+bc), este total absurdă pentru orice persoană aflată la primul contact cu ideea de număr complex: “de ce să definesc astfel înmulţirea?, nu are sens!, nu înţeleg nimic!”, aceasta va fi reacţia oricărei persoane normale la cap. Dar oare, cine a inventat această ciudăţenie şi cum ne-am pricopsit cu ea în şcoli?

Pentru a răspunde primei întrebări, recomand oricui să studieze istoria evoluţiei şi cristalizării teoriei despre numere complexe, mai ales cea legată strict de acestea, din secolele XVIII-XIX. De pildă, faptele sunt prezentate magistral în lucrarea despre care am mai vorbit şi cu alte ocazii: Paul J. Nahin, O poveste imaginară, istorea numărului radical din –1, Ed. Theta, Bucureşti, 2000. Următorul aliniat este preluat din această lucrare, cu citatul strict prezentat înclinat:

Introducerea numerelor complexe ca perechi ordonate cu operaţiile anexate a fost prezentată pentru prima dată de matematicianul irlandez William Rowan Hamilton în 1835, într-o lucrare despre cupluri algebrice (aşa le-a numit el iniţial), în faţa Academiei irlandeze. Cele două operaţii sunt parte a unei “definiţii şi, în consecinţă, nu au nevoie de alte explicaţii. În teoria lucrării respective ele pică deci din senin dar, este clar că Hamilton era motivat de modul cum funcţionează numerele complexe. Cu alte cuvinte, cuplurile pure şi abstracte (a, b) nu sunt altceva decât un alt mod de a scrie a + ib. Hamilton credea totuşi că această notaţie este preferabilă pentru că evită folosirea absurdului radical din –1. El are chiar un comentariu comic despre această alegere: Cei care vor citi cu atenţie remarcile la această teorie … vor vedea că aceste notaţii nu sunt arbitrar alese.” (citat de la pag. 71).

Deci chiar şi Hamilton recunoştea la acel moment că totul este doar un joc, o aparentă nouă teorie care dă impresia că elimină din proces înţelegerea intuitivă a fenomenului numerelor complexe. Cum s-a ajuns însă ca o lucrare pur ştiinţifică să aterizeze după 150 de ani în manualele şcolare pentru elevi de 15 ani (eu atâta aveam în 1982 când am învăţat lecţia în clasa a IX-a), aceasta este un alt subiect, despre care am încercat unele lămuriri în eseul în care am prezentat Reforma uitată din 1978-1981, la pag. 4-9, din Reforma uitată (partea I).

Dar, presupunând că şi-ar propune schimbarea stilului de predare din riguros axiomatic într-unul naiv intuitiv, corect pedagogic, cum ar putea un profesor să predea în acest fel? (plecând de la premiza că îşi doreşte o predare din care elevii săi să şi înţeleagă mai mult). Căutările mele mi-au arătat (cu vârf şi-ndesat) că la majoritatea lecţiilor de liceu se găsesc forme destul de bune în manualele româneşti oficiale din anii ’60-’70. După 2-3 ture de căutări şi încercări (ca să nu spun experimentări, că imediat sare careva că “experimentezi pe elevi”), orice profesor deschis la minte va începe şi el să-şi găsească o formă mai bună de predare a unui capitol. De vreme ce ministerul, împreună cu toate structurile sale de organizare a predării în şcoli, nu sunt în stare a ne oferii astfel de modele, este evident că profesorul trebuie să devină el însuşi un căutător.

În materialul de faţă am abordat spre exemplificare două teme ce îmi sunt deosebit de dragi, numerele complexe şi combinatorica. Alegerea celor două subiecte a fost una subiectivă; oricare temă de studiu din liceu ar trebui prezentată în mod similar. Gradul de naivitate mai crescut se referă în primul rând la introducerea noilor concepte; odată ce elevii s-au obişnuit cu acestea (după 2-3 ore), predarea nu mai diferă foarte mult de ceea ce cunosc majoritatea profesorilor. Trebuie însă înţeles că la fiecare pas teoretic important ce se face în necunoscut, trebuie folosită o abordare intuitiv-naivă. Părerea mea personală este că o cale ce foloseşte cât mai des predarea prin problematizare, în care elevul să descopere singur paşii lecţiei, sub îndrumarea profesorului, în urma întrebărilor ajutătoare ale profesorului, aceasta este pe durată cea mai sănătoasă cale de a parcurge materia. Forma de lucru ar trebui să fie în principiu următoarea: noi, profesorii, îi îndrumăm pe elevi pe o cale de (re)descoperire a  temei studiate. Cine a făcut cercetare reală ştie cât de naiv gândeşte cel care se aventurează într-un teritoriu virgin, pe care nu l-a mai parcurs nimeni înaintea sa. Singurele sale repere de care se poate ajuta sunt lucrurile pe care deja le cunoaşte din urmă, cât şi logica bunului simţ. Într-un astfel de stil trebuie să “descopere” şi elevii noua temă. Cine a făcut cercetare adevărată, nu compilare din materiale deja existente (aş numi aceasta pseudo-cercetare, sau cercetare secundară), acela înţelege despre ce vorbesc aici. Descoperirea temei de către elev nu este însă una haotică, ci este îndrumată cât mai eficient de către profesor. Această formă eu o numesc predare prin întrebări sau, ceva mai pretenţios, predare prin descoperire, care este o formă extremă în predarea prin problematizare. Într-o astfel de formă de predare, la sfârşitul lecţiei, sau şi mai bine ora următoare, se organizează, se ordonează noile cunoştinţe, acestea căpătând forma unei lecţii de memorat. Elevii însă nu mai trebuie să le memoreze pentru că majoritatea dintre ei deja le-au înţeles. În schimb încep să dobândească şi aptitudini mai mature matematic, în sensul că învaţă pe viu cum să ordoneze din punct de vedere riguros matematic nişte cunoştinţe deja dobândite intuitiv. Şi oricum, aşa cum am precizat deja: marii matematicieni, monştri sacri Wessel şi Argant, Gauss şi Hamilton pe acest drum au mers. Hamilton cu teoria sa a fost ultimul, nu primul, pe drumul înţelegerii numerelor complexe. Nu înţeleg de ce elevii trebuie să parcurgă drumul invers, ca să nu spun “pe dos”.

Tema despre introducerea numerelor complexe nu o mai abordez in extenso în eseul de faţă; am prezentat-o pe larg în articolul Apariţia numerelor complexe din Caietul de matematică Pentagonia Nr. 2 din aprilie 1998 la pag. 14, într-o propunere personală, dar şi în articolul Reforma uitată la pag. 19-20, într-una din formele existente într-un manual dinaintea reformei de la sfârşitul anilor ’70.

Să analizăm în continuare introducerea principalelor elemente de combinatorică într-o formă mai inteligibilă pentru elevul care se întâlneşte prima dată cu acest subiect. Nu mă voi referi în cele ce urmează la întregul capitol, ci doar la tripleta permutări, combinări şi aranjamente. Să analizăm pentru început ordinea în care se pot parcurge acestea. În manualele din ţara noastră ordinea este P-A-C. Oare ce alte posibilităţi există (nu glumesc defel) şi care din acestea ar fi mai potrivită elevilor? În cele ce urmează mă voi referi la două dintre celelalte cinci variante, anume la P-C-A şi la C-A-P.

După părerea mea (preluată în urmă cu ani buni de la un coleg drag), ordinea P-C-A este cea mai logică din punct de vedere a fenomenelor studiate. Anume, permutările studiază un fenomen, cel mai simplu şi accesibil; combinările vin apoi studiază alt tip de fenomen, unul clar mai complicat; în final vin aranjamentele care studiază o situaţie ce combină cele două fenomene deja cunoscute. Ani de-a rândul am predat cele trei lecţii în această ordine şi pot să spun că predarea decurge foarte bine astfel.

De curând am participat în Germania, la Kassel, la un curs pentru profesori Waldorf de liceu, la o serie de discuţii despre predarea Combinatoricii, seminar în care profesorul Steffen Brasch a prezentat predarea într-o ordine ce ar putea fi sintetizată ca C-A-P. Mai exact, el se ocupa de cunoaşterea practică, pe exemple, a combinărilor, deducând de aici triunghiul lui Pascal, apoi, din exemple mai ciudate reiaşeau aranjamentele, iar permutările apăreau şi ele undeva ca exemple foarte simple. De-abia în final vorbea dânsul de o sintetizare teoretică, unde veneau şi clasicele formule (parcursul istoric acesta a fost). Nu am înţeles toate detaliile – timpul a fost foarte scurt – dar am luat notiţe pe care cândva le voi studia în amănunt. Se înţelege deci că nu am glumit deloc atunci când am întrebat câte posibilităţi există de a ordona  cele trei lecţii.

Dar cum ar trebui prezentate aceste trei lecţii conform principiilor matematicii naïve? Pentru că, este clar, vorbim despre primul contact al elevilor cu tema respectivă. Eu am plecat de fiecare dată de la probleme tip şi nu de la teorie. În cazul introducerii noţiunii de permutare, problema tip ce mi-a fost sugerată de tatăl meu este următoarea:

Problema trenului ROGVAIV: Un tren are şapte vagoane, vopsite fiecare într-una din culorile curcubeului (le notăm: R = roşu, O = orange, Ve = verde, etc.). În câte feluri poate fi aranjată garnitura acestui tren?

Formulele de calcul ar trebui să apară în viaţa elevilor drept teoreme – deduse intuitiv sau demonstrate riguros –  şi în nici un caz ca definiţii. În cazul permutărilor, în predarea prin problematizare, plecăm de la problema vagoanelor şi începem să cercetăm situaţia: dacă ar fi doar două vagoane, câte variante de ordonare a garniturii există? Două, RG şi GR. Dacă am avea trei vagoane, câte variante avem? Şi elevii încep să le caute. Şase, vine răspunsul. Dar dacă am avea patru vagoane?  Îi mai lăsăm să caute, depinde de nivelul elevilor din clasă, dar poate aici este momentul să intervenim şi să reluăm lucrurile ordonat, adică să-i învăţăm cum să-şi aranjeze ordonat toate variantele, pentru că altfel mulţi elevi le dau haotic, iar de la patru vagoane încep să piardă anumite variante. Când aştern ordonarea pe tablă, iau pentru început şi cazul particular cu un vagon. Urcăm pe acest drum până când cineva din clasă observă ce se întâmplă (desigur că aranjarea într-o schemă sugestivă a tuturor variantelor la trei, respectiv la patru vagoane, este hotărâtoare pentru înţelegerea fenomenului). În momentul în care apare ideea de rezolvare, elevii inteligenţi matematic o vor aplica imediat şi vor ajunge rapid la răspuns; ei au înţeles modelul logic după care funcţionează “jucăria” şi gata. Alţii însă, vor vrea să facă mai departe ordonările şi în cazurile cu mai multe vagoane. Putem să-i lăsăm să le scrie pe toate la 5 vagoane (poate acasă), dar vor trebui să înţeleagă că numărul creşte prea tare, ajungând în imposibilitatea de cuprindere în scris a tuturor variantelor. Aici poate îi ajutăm pe aceştia cu o formă de grupare a unor variante (acolade, încadrare într-un dreptunghi etc.) astfel încât să poată şi ei face saltul logic de la realizat practic cu creionul la văzut schemei doar în minte.

După rezolvarea problemei sintetizăm totul într-o teorie. Aici definim operaţia de factorial (eu îi pun pe elevi să facă şi tabla factorialului, cu rezultate calculate de către toţi elevii  până la 10!, pentru a simţi cât de explozivă este aceasta). Ordinea intuitivă ar cere chiar realizarea tablei factorialului mai întâi, apoi generalizarea într-o definiţie. Apropos, factorialul se poate defini în două variante: n! = 1 ∙ 2 ∙ 3 ∙ … ∙ n sau invers n! = n ∙ (n-1) ∙ (n-2) ∙ … ∙ 3 ∙ 2 ∙ 1; fiecare este uneori mai avantajoasă; depinde de situaţie. Apoi dăm definiţia permutărilor şi, cu titlul de teoremă, formula P_n = n! pentru calculul acestora. În continuare vin alte probleme aplicative ale premutărilor, pe care elevii sunt învăţaţi să le rezolve direct, prin formula deja dedusă, având însă în cap modelul celor şapte vagoane. De pildă, în câte feluri pot fi aranjaţi opte alergători pe cele opt culoare la proba de 100m plat? Sau: avem un set de trei ghivece diferit colorate; în câte feluri le putem aranja pe pervaz? etc. O astfel de temă este foarte simplă, pentru că în principiu trebuie doar luate rezultatele din tabla factorialului. Ora viitoare vom face şi exerciţii de calcul steril cu noua operaţie de factorial şi lecţia intră pe făgaşul cunoscut.

O observaţie specială vine aici în legătură cu aspectul psihologic al numerelor mari, cu care ne confruntăm din belşug la aceste probleme. Toată lumea a ajuns imună la aceste numere mari cu care ne bombardează societatea prezentului. Pentru a le înţelege cât sunt de mari, trebuie să le aducem într-un reper personal al vieţii de zi cu zi. De pildă, după prima oră, cu problema trenului ROGVAIV, le putem da elevilor ca temă următoarea suplimentare a acestei probleme:

Mecanicul trenului ROGVAIV: Un mecanic tânăr, aflat la început de carieră, primeşte în îngrijire trenul ROGVAIV şi îşi propune să aranjeze la fiecare cursă a trenului cele şapte vagoane în altă ordine. Trenul respectiv face în fiecare zi o cursă “dus” şi o cursă “întors”, iar mecanicul nostru, după cursa dus mută doar locomotiva şi schimbă plăcuţele de numerotare a vagoanelor, aşa încât poate bifa în fiecare zi câte două ordonări diferite. În câţi ani va reuşi să epuizeze toate ordonările posibile (fără a avea nici o singură zi liberă)? Dar dacă ar fi vorba de un tren cu opt vagoane? Faceţi problema şi observaţi ce efect are rezultatul asupra dvs. În acest moment matematica devine cu adevărat impresionantă.

Este evident că lecţia despre combinări este mult, mult mai grea decât cea despre permutări, şi nu mi-am propus pentru acest eseu o prezentare completă a acesteia (vezi Anexa din final). Aranjamentele, pe poziţia a treia, apar apoi foarte uşor, provocarea pentru elevi fiind doar în a observa că trebuie îmbinate cele două principii, de la permutări şi de la combinări.

Pentru eseul de faţă am urmărit doar exemplificarea pe cazul permutărilor a felului cum se poate introduce o noţiune nouă prin problematizare şi nu prin prelegere riguroasă. De la o astfel de oră elevii pleacă cu inima plină de bucurie şi cu mintea plină de gândire. Şi când spun asta, vorbesc de toţi elevii care au fost dispuşi să participe la jocul găsirii soluţiei. Ştiu că durează mai mult, dar efectul asupra elevilor este net superior.

Anexă  Problematica introducerii combinărilor presupune, pe lângă găsirea problemei tip cea mai potrivită, şi lămurirea următorilor paşi: abordarea problemei intuitiv, deci fără definiţie; corelarea cu formulele binomiale deduse elementar algebric, apariţia triunghiului lui Pascal; lecţia numită generic Binomul lui Newton; deducerea formulei de calcul a combinărilor; îmbinarea celor două tendinţe, calculul algebric, sec, riguros ştiinţific, pe de-o parte, şi problemele aplicative de o diversitate uluitoare, pe de altă parte, conştientizând că acest capitol este ultimul din viaţa elevilor în care apar probleme frumoase cu caracter de matematică distractivă.

Titus Grigorovici

19 sept. 2016

Chiar dacă nu într-o formă completă, extremă, academică, specifică facultăţilor, rigurozitatea axiomatică în matematica poate fi introdusă deja din clasele liceale. Aceasta însă cu o singură condiţie: să fie abordate din punct de vedere riguros axiomatic teme deja cunoscute de către elevi, teme cu care aceştia s-au familiarizat înainte pe calea naturală intuitiv-naivă. În acest sens revenim scurt în gimnaziu unde, în linii mari, sunt studiate trei mari teme: aritmetica, algebra şi geometria tradiţională moştenită de la Euclid. Elemente din aceste trei mari domenii ar putea fi tratate mai riguros axiomatic la o a doua mare trecere în clasele liceale, şi chiar aşa şi erau acestea prezentate în manualele de clasa a IX-a începând din 1978.

Toate bune şi frumoase, cu o singură “mică” problemă: două dintre cele trei mari teme gimnaziale au fost scoase din materia de liceu la schimbările din învăţământ pe care le denumim ad-hoc “reforma din 1997”. Nici aritmetica, nici geometria euclidiană tradiţională nu se mai regăsesc printre capitolele de studiu din programele de liceu ce au urmat. Ca o mică divagaţie trebuie menţionat aici că acesta este motivul pentru care elevii privesc cât-de-cât pozitiv temele care amintesc de ceva cunoscut din Gimnaziu, adică unele teme de algebră. Dimpotrivă, scurta incursiune gimnazială în trigonometrie nu poate fi privită ca temă deja cunoscută în liceu, pentru că în afara celor cinci cuvinte de vocabular comune (trigonometrie, sinus, cosinus, tangentă şi cotangentă :-), nimic din lecţia orientată geometric în Gimnaziu nu reapare în trigonometria de liceu.

Aş da un exemplu în acest sens, al importanţei aşa-numitei predări în spirală: pe vremuri am avut o elevă foarte slabă la matematică, care primea “cinci-ul” doar de milă, pentru că mai mult nu putea. Totuşi, printr-o minune, cu multă strădanie, a reuşit să-şi ia nota de trecere la examenul de capacitate, aşa că a ajuns la liceu. Fiind clasă de profil uman (ce denumire sugestivă!), colegii nici nu protestau că ea primea nota 5 cam nejustificat, o acceptau ca atare. La începutul clasei a XI am introdus câteva ore de “sisteme de trei ecuaţii cu trei necunoscute cu rezolvări elementare prin substituţie şi reducere” (vechile sisteme din culegerile lui Grigore Gheba, cu materie de clasa a VIII-a). Surpriza de proportii a apărut la lucrarea de control, unde eleva noastră a scos nota 9, având rezolvări profund diferite faţă de colega ei de bancă (elevă de 9-10), de la care de obicei copia pentru a scoate cumva “cinci-ul”. Ceilalţi din clasă s-au indignat, dar au înţeles când le-am explicat că rezolvările sunt total diferite. Întrebată cum şi de ce, eleva noastră a spus simplu: semănau cu ceva ce mai făcusem, aşa că le-am înţeles (semănau cu sistemele de două ecuaţii cu două necunoscute, care atunci erau încă în clasa a VII-a). Interesant este faptul că ulterior, la lecţiile total noi ce au mai urmat, a scăzut din nou, dar de la acea întâmplare s-a stabilizat undeva între 5 şi 6, adică nu a mai fost nevoie să o trec “de milă”. Elevii “tari” la matematică sunt mai rezistenţi la fenomen lecţiilor total noi, dar pe durată se uzează şi ei emoţional faţă de această materie care “îi ţine tot timpul în lecţii şi teme total noi”.

Revenind la subiectul eseului de faţă, temele noi de studiu ce apar în liceu – adică majoritatea – au nevoie de o introducere mai naivă, altfel profesorul “vorbeşte cu pereţii” (iar dacă nu-şi dă seama că “vorbeşte cu pereţii” înseamnă că are deficienţe mari în zona percepţiei empatice a elevilor, în general a clasei). Chiar dacă elevii de liceu sunt deja selectaţi pe real şi uman, noi vorbind aici de elevii de la profilul real, totuşi la aceste vârste marea majoritate au nevoie de o introducere cu un grad de naivitate destul de ridicat a noilor teme de studiu (la orice ştiinţă, nu doar la matematică). Altfel, cei cu posibilităţi financiare fug toţi să-şi ia profesor de ajutor în particular.

De-abia la facultate, şi doar cei care au făcut pasul conştient spre matematică, doar aici tinerii sunt de obicei capabili a aborda o temă direct, din prima, riguros axiomatic. Pentru aceasta ei trebuie însă să se fi exersat înainte în tratarea axiomatică a unei teme matematice. Dar cele mai bune exersări sunt cele pe teme deja cunoscute dinainte în mod intuitiv naiv. Din păcate însă acestea au cam fost scoase din materie. Cunoaşterea metodelor de introducere a unei teme riguros axiomatic la lecţii total noi este percepută de către elevii de liceu ca suferinţă intelecuală, fiind profund neatractivă şi făcând din matematică o materie total neiubită. Acesta este motivul pentru care, începând de prin 2000, profesorii din facultăţile de matematică resimt tot mai puternic nepregătirea studenţilor pentru activitatea la acel nivel.

Ce ar trebui făcut în aceste condiţii? Concluziile despre corecturile ce ar trebui aplicate sistemului se trag de la sine.

Titus Grigorovici

La începutul anului şcolar 2016-2017

Matematica naivă
Matematica naivă, exemple (1)
Matematica naivă, exemple (2)

Dacă ajungi într-o capitală mondială ca turist – de pildă Roma – ai foarte multe de vizitat. Fie că ajungi la Roma pentru două zile, fie că ajungi pentru o săptămână, oricum ai aceeaşi problemă: să stabileşti care sunt cele mai importante locuri de vizitat în sejurul tău. Pentru alegerea respectivă apelezi la un ghid: sau mergi cu un grup organizat cu un ghid, sau cumperi un ghid scris, sau te îndrumă o cunoştinţă. De la acesta îţi doreşti să fi îndrumat în ordinea importanţei şi vei fi supărat dacă ai fi fost plimbat de pildă la nenumărate biserici, dar nu ai văzut Columna lui Traian.

Capitolul despre Cerc se aseamănă foarte mult cu un astfel de oraş: sunt foarte multe de văzut, iar elevii trebuie îndrumaţi în funcţie de timpul alocat şi de nivelul clasei, astfel încât să vadă ce este mai important în condiţiile date. Din păcate şi aici programa gafează profund chinuind copiii cu o lecţie fără sens, rămasă acolo din vremuri de demult, ca parte dintr-o construcţie de rigurozitate universitară ciudată. Să analizăm situaţia.

Capitolul începe cu lecţia introductivă despre definiţie, rază, diametru, coardă, arc, semicerc etc. Lecţia a doua face legătura între măsura de unghiurilor la centru şi măsura arcelor de cerc. Să analizăm lecţia a treia: Coarde şi arce în cerc; diametru perpendicular pe o coardă; arce cuprinse între coarde paralele; coarde egal depărtate de centru (lecţie pe care unii profesori o şi întind pe două ore. Pentru ce este bună această lecţie? La ce îi folosesc aceste teoreme elevului? Analizând “utilitatea” lor, ajungem la concluzia că acestea reprezintă trei sferturi dintr-un drum ce ar trebui să demonstreze că tangenta la cerc este perpendiculară pe raza dusă în punctul de contact. Această ultimă teoremă însă nu se demonstrează, aşa că teoremele din lecţia a treia nu îşi au nici un rost. Elevii sunt chinuiţi gratuit cu nişte teoreme fără sens! Singurul aspect ce se opţine clar este înverşunarea şi scârbirea şi mai profundă a elevilor împotriva geometriei.

Dacă ne întoarcem la ideea de matematică naivă, teoremele din lecţia a treia nu au pentru elevi niciun rost. În primul rând, că demonstrează adevăruri intuitiv evidente. Apoi, informaţiile respective nu se folosesc în nici o problemă: profesorii au dificultăţi în a găsi aplicaţii la aceste teoreme! Singurul raţionament ce se foloseşte de aici este faptul că triunghiul determinat de două raze şi o coardă este isoscel. Dar pentru asta oricum nu ai nevoie de vreo teoremă specială.

Aici se ridică o mare întrebare: pentru ce parcurgem anumiţi itemi? De pildă, de ce parcurgem o anumită teoremă? În principiu, pentru elevi această întrebare are două-trei răspunsuri: fie pentru utilitatea sa (ca aplicaţii în probleme sau în susţinerea unei alte teoreme importante), fie pentru demonstraţia sa deosebită. Dacă o teoremă este foarte importantă prin prisma aplicaţiilor, dar are o demonstraţie foarte grea, atunci teorema poate fi dată naiv, pe încredere, adică fără demonstraţie, elevii bucurându-se în schimb de aplicaţii uşoare. Este cazul teoremei tangenta la cerc este perpendiculară pe raza dusă în punctul de contact, care permite aplicaţii uşoare cu teorema lui Pitagora, dar şi parcurgerea în continuare a teoremei “ciocului de cioară” despre cele două tangente de la un punct la un cerc. Teorema despre măsura unghiului înscris în cerc are şi o demonstraţie frumoasă, dar şi aplicaţii interesante.

Nu-i clar ce înţelege onor Ministerul prin propuneri inovative de programă, dar eu consider că astfel de criterii ar trebui să stea la baza alegerii lecţiilor şi a itemilor de parcurs. De exemplu, eu din prima lecţie de la cerc concluzionez că două raze împreună cu coarda determinată de acestea formează un triunghi isoscel, după care elevii şi primesc aplicaţii de calcul cu teorema lui Pitagora în triunghiul isoscel respectiv. În lecţia a doua parcurg Cercul lui Thales (două coarde cu un capăt comun iar celelalte două capete diametral opuse sunt perpendiculare), demonstată cu triunghiuri isoscele, şi teorema cu tangenta la cerc este perpendiculară pe raza dusă în punctul de contact, fără demonstraţie. Din acest moment am multe aplicaţii, elevii găsind un sens în lecţiile acestui capitol. Iată şi un exemplu de aplicaţie în sensul construcţiilor cu rigla şi compasul: folosind Cercul lui Thales se pot trasa înălţimile într-un triunghi dat, doar cu rigla şi compasul.

În ultimii ani am încheiat acest capitol cu două teoreme duale, în pereche, ce nu le parcurg pentru vreo aplicaţie a lor, ci doar pentru frumuseţea demonstraţiei. Fiecare demonstraţie în sine nu este deosebită. Privite însă împreună, cele două teoreme cu demonstraţii corespunzătoare trezesc în rezolvitor acea stare mult dorită de uimire, caracterizată simplu printr-un mare “UAU!”. Este vorba despre proprietatea unghiurilor patrulaterelor înscrise în cerc (inscriptibile), respectiv proprietatea dual-omoloagă a laturilor patrulaterelor circumscrise unui cerc (circumscriptibile). În imaginea de mai jos puteţi vedea blocul principal al acestei lecţii

Numărul π nu apare în capitolul despre cerc, ci într-un capitol artificial, imediat după cerc. De ce îl cataloghez drept artificial? Pentru că acest capitol dă mai multă atenţie celor trei poligoane regulate importante decât drumului către numărul π. Oricum, drumul respectiv nu este parcurs în lecţii, chiar existând profesori care “o lălăie” într-atăt încât nici nu mai ajung la numărul π în clasa a VII-a.

Pentru început, în acest proces noi măsurăm circumferinţa diferitor obiecte circulare şi calculăm raportul faţă de diametrul cercului, obţinând diferite valori între 3 şi 3,2 (la diferite oale este cel mai folositor un metru de croitorie). Ca exemplu mai special, în curtea şcolii noastre avem un teren circular de beton; vă puteţi închipui ce distracţie a fost în ultimii ani în cadrul Săptămânii Şcoala Altfel, când am măsurat cu o sfoară şi cu mulţi elevi circumferinţa terenului.

La un nivel intelecual mai înalt, după ultima problemă de la Examenul de Evaluare Naţională din iunie 2016, eu oricum m-am hotărât să parcurg şi octogonul regulat (cu unghiul la centru de 45^o la fiecare felie-triunghi isoscel) cât şi dodecagonul regulat (cu unghiul la centru de 30^o), studiind perimetrul şi aria, şi procesul în care acestea se apropie de valorile cercului. Apropos, verificaţi cât de uşor se poate arăta că aria dodecagonului regulat înscris în cercul de rază r este exact 3r², folosind pentru calcularea ariei fiecărei felii 1/12 doar teorema despre cateta opusă unghiului de 30^o. Pentru calcularea perimetrului poligonului regulat cu 12 laturi trebuie însă muncit însă ceva mai mult. Lucrând cu aproximări de trei zecimale, se obţine în final raportul perimetru/diametru de 3,10 (doar pentru elevii de 10).

O apropiere mai bună de valoarea lui π am obţinut, mult mai uşor şi pe mintea tuturor, printr-o altă abordare de tip Laboratorul de matematică. Astfel, elevii au desenat pe caietul de matematică, cu pătrăţele de 0,5² = 0,25cm², un cerc cu raza de 5cm (prin triunghiul egiptean, avem garanţia unei exactităţi deosebite în câteva puncte de pe cerc). Elevii au trebuit să determine pur şi simplu aria discului prin aproximaţie, numărând cm², jumătăţile şi sferturile, cât şi aproximări ale resturilor pătrăţelelor rămase. Rezultatul de 78 : 25 = 3,12 pentru raportul dintre aria cercului şi aria pătratului pe rază este unul foarte bun şi orice elev îl înţelege. Vedeţi această parte de lecţie cu matematică naivă în următoarea imagine. Trecerea de la aceste rezultate (atât la perimetrul cercului cât şi la aria discului) la cunoscutul 3,14 se face pe încredere şi toţi elevii sunt bucuroşi că au înţeles despre ce este vorba.

1 august 2016

Prof. Titus Grigorovici

Vezi și: Matematica naivă, Matematica naivă, exemple (1)

Unori Ministerul Educaţiei nu mai ştie ce să facă, aşa că oferă profesorilor ocazia să vină ei cu o propunere inovativă de programă. Ce înseamnă aceasta şi în ce direcţie trebuie o astfel de propunere să fie inovativă, asta nu este clar, deşi, poate era mai bine dacă ministerul împreună cu toate structurile sale de management a educaţiei dădeau nişte linii ghidante. Noi, oamenii de rând nu putem vrăji “la comandă” idei care să fie cu adevărat novatoare, dar totodată şi verificate în sensul eficienţei în condiţiile din ţara noastră. Pe de altă parte, nu se ştie nici odată “de unde sare iepurele”, adică de unde apare o idee bună. Am prezentat în eseul despre matematica naivă câteva idei despre acest nou concept de prezentare a cunoştinţelor matematice în funcţie de posibilităţile şi nevoile vârstelor elevilor, nu în funcţie de dorinţele foştilor diriguitori din Olimpul matematicii româneşti. Totuşi, conceptul este neclar şi prin faptul că îi lipsesc exemple de aplicare în viaţa de zi cu zi. Pentru aceasta voi încerca să prezint câteva situaţii din matematica gimnazială, acolo unde gradul de naivitate necesar este încă mai mare.

Să luăm un exemplu dublu pentru a clarifica lucrurile. Una din marile “minuni” cu care matematica gimnazială s-a catadicsit la reforma din 1980 a fost demonstraţia prin metoda reducerii la absurd. Aceasta era însă atât de inaccesibilă elevilor încât nu a reuşit să penetreze nici măcar fondul de probleme pentru olimpiade. 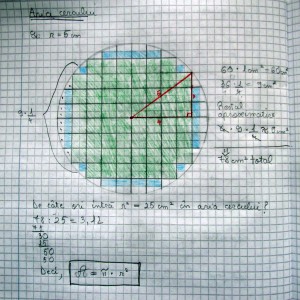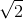Totuşi, era acceptată oficial şi păstrată în materie datorită celor două mari demonstraţii tradiţionale ce o foloseau: demonstrarea iraţionalităţii lui  venită de la marele Euclid şi demonstrarea congruenţei unghiurilor alterne interne venită din axiomatizarea radicală a geometriei din jurul anului 1900 (amândouă erau în materia clasei a VI-a, dar capitolul despre rădăcina pătrată a fost mutat la sfârşitul anilor ‘90 în clasa a VII-a). Aceste demonstraţii nu se mai fac de mult cu elevii la clasă, dar abordarea şi ordonarea materiei în funcţie de ele este păstrată şi la ora actuală, fără ca lumea să fie conştientă de acest fapt. Să lămurim pe rând cele două situaţii.

Ordonarea materiei în jurul temei TRIUNGHIUL era în anii ‘80 următoarea: triunghiuri şi construcţia lor; cazurile de congruenţă ale triunghiurilor; proprietăţile triunghiurilor isoscele; drepte paralele; axioma paralelelor şi unghiuri formate de două drepte paralele cu o secantă; suma unghiurilor în triunghi (citat din cuprinsul manualului de clasa a VI-a, autori Ion Cuculescu, Constantin Ottescu, din cele două exemplare ce le am pe-acasă, cel din 1979 şi cel din 1988). Punctul central al acestei secvenţe de lecţii era teorema de legătură între congruenţa unghiurilor alterne interne şi paralelismul dreptelor cu demonstrarea prin reducere la absurd, folosind congruenţa a două triunghiuri. De-abia după aceasta se putea demonstra şi suma unghiurilor în triunghi.

Ordonarea materiei la ora actuală este cam aceeaşi, în afara de demonstrarea ciudatei teoreme care nu se mai face la clasă de cca. 20 ani. Actualmente, legătura între dreptele paralele şi congruenţa unghiurilor alterne interne se face pe încredere, pentru că aşa zice profesorul. O a doua diferenţă faţă de anii ’80 este că depărtarea dintre prima lecţie despre triunghi şi momentul când se învaţă suma unghiurilor a crescut şi mai mult, între acestea parcurgându-se în prezent şi un capitol serios despre perpendicularitate.

Ce se întâmplă în aceste condiţii la clasă, depinde de la un caz la altul. Din multele variante în care elevii află despre acea sumă miraculoasă de 180^o, doresc să evoc una, de care am aflat anul şcolar trecut. Profesorul de la clasă parcurge materia conform programei; aşa, măcar elevii nu ştiu despre ce-i vorba şi basta! Dar în piesa de teatru a acelei şcoli mai exista şi personajul numit profesorul de la opţional, care nu se simţea deloc dator a respecta programa colegului. Astfel, elevii află la opţional că suma unghiurilor ar fi de 180^o, cu observaţia evidentă că profu’ de la clasă încă nu poate/nu vrea să v-o divulge. Eu nu doresc întoarcerea la vremurile de rigurozitate extremă din anii ’80-’90, dar nici o batjocură de felul acesta nu accept, la adresa gândirii logico-matematice pe care tocmai ne pregătim să le-o inducem elevilor.

O propunere inovativă simplă de aplicat de către orice profesor, pentru această parte de materie, ar fi studierea unghiurilor formate de două paralele cu o secantă înaintea lecţiei despre triunghi. Aceasta se poate face la fel ca în formatul actual, adică deducând intuitiv congruenţa unghiurilor corespondente, alterne interne etc. Eu, de pildă, folosesc aici o translaţie prin care justific congruenţa unghiurilor corespondente, iar apoi celelalte congruenţe se deduc uşor cu unghiuri opuse la vârf. Această mutare îmi permite includerea în prima lecţie despre triunghi a sumei unghiurilor, cu demonstraţie cu tot! Adică, din prima lecţie elevii învaţă definiţia, elementele, perimetrul şi suma unghiurilor în triunghi, având din start cea mai importantă proprietate a tringhiului. Nu mai insist cât de mult se simplifică lecţiile ulterioare despre triunghi, dacă avem de la început suma unghiurilor. Eu predau în acest format din anul şcolar 1994-1995 şi pot doar să privesc cu durere cum sunt chinuiţi majoritatea elevilor din celelalte şcoli, în formatul vechi. Ca o ultimă observaţie la acest subiect, trebuie precizat că ordinea din această propunere este similară cu ordinea existentă în manualele din anii ’70 ale profesorului A. Hollinger.

Abordarea temei despre RĂDĂCINA PĂTRATĂ se făcea în anii ‘80 în felul următor: rădăcina pătrată dintr-un număr natural pătrat perfect; rădăcina pătrată dintr-un număr raţional nenegativ; rădăcina pătrată cu aproximaţie de o unitate prin lipsă dintr-un număr raţional nenegativ; numere iraţionale; extragerea rădăcinii pătrate (citat din cuprinsul manualului de clasa a VI-a din 1979, autori C. P. Popovici, I. C. Ligor). Primele lecţii prezentau câteva elemente introductive greu de înţeles pentru elevul de rând, după care se trecea la demonstrarea iraţionalităţii lui  (demonstraţia arhi-cunoscută prin reducere la absurd), iar în final apărea şi algoritmul de extragere a rădăcinii pătrate. Exerciţiile rămâneau însă în zona aritmetică de extragere exactă sau aproximativă a rădăcinii pătrate. Urma un capitol despre mulţimi elementare de numere, în care se prezentau mulţimile de numere naturale, întregi, raţionale respectiv reale. Acolo găsim câteva întrebări în care copiii erau verificaţi dacă ştiu că ş.a. nu sunt raţionale. Atât! Tot restul clasei a VI-a elevii rămâneau în zona aritmetică a rădăcinii pătrate pe care o exersau cu orice ocazie (mai urmau capitolele despre rapoarte şi proporţii, şi despre procente). De-abia în clasa a VII-a elevii treceau la calcule cu numere iraţionale, calcule ce reprezintă nivelul algebric al operaţiilor cu radicali.

Odată cu mutarea capitolului despre rădăcina pătrată în clasa a VII-a, mutare efecuată la finalul anilor ’90, cele două părţi – cea aritmetică şi cea algebrică – au fost cumulate într-un capitol, partea aritmetică pierzându-şi mare parte din perioada sa de aplicaţie/dospire. Actualmente, elevii stau cca. o săptămână în starea aritmetică, după care se trece la calculul algebric cu numere iraţionale.

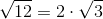Oare, este bine aşa? Ce înţelege un elev, dacă scrie  (forma algebrică) şi ce înţelege el din forma aritmetică 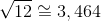? Forma aritmetică este una clară, practică, chiar dacă nu este super-exactă. Forma algebrică este exactă, dar de neînţeles pentru mintea umană normală. Elevul ar avea nevoie de o perioadă de acomodare cu noua operaţie, timp în care să calculeze rădăcina pătrată, în funcţie de natura sa (exactă sau aproximativă), după care, de-abia apoi să treacă la calcule algebrice cu numere iraţionale. În ţările din vestul Europei aşa se face.

Cât despre demonstraţia iraţionalităţii lui , unii profesori nu o mai prezintă (adică merg pe încredere), pe când alţii o fac la clasă, dar elevii în general nu o înţeleg. Părerea mea personală estă că aceasta reprezintă un item clar pentru materia de clasa a IX-a.

O propunere inovativă simplă de aplicat de către orice profesor, pentru această parte de materie, ar fi împărţirea temei în două părţi distincte. De pildă se poate rămâne în starea aritmetică în semestrul I din clasa a VII-a, iar apoi se trece în semestrul II la calculele în forma algebrică cu numere iraţionale. Desigur că s-ar putea reveni tot aşa de bine şi la forma veche, cu partea aritmetică în clasa a VI-a, iar partea de tratare algebrică de-abia în clasa a VII-a.

Un aspect aparte al acestui subiect îl reprezintă forma de aplicare a rădăcinii pătrate în cadrul calculului cu teorema lui Pitagora, în cazul rezultatelor ne-exacte. Calculele de lungimi, perimetre şi arii reprezintă partea practică a geometriei plane, iar la acestea sunt mult mai clare calculele aproximative ale rădăcinii pătrate (adică forma aritmetică). Prin acestea elevul îşi poate dezvolta o percepie naturală şi un bun-simţ al calculului (de exemplu, cam cât este de lungă diagonala unui pătrat cu latura de un metru, dar şi multe alte exemple “practice”). Trecând abia ulterior şi la calcule cu exprimarea rezultatelor în formă exactă iraţională, le permite elevilor realizarea unei înţelegeri naturale a matematicii şi a conexiunilor dintre elementele acesteia.

De pildă, eu încep materia clasei a VII-a cu un mega-capitol compus din trei părţi distincte: 1) Rădăcina pătrată şi extragerea acesteia, cu rezultate naturale, respectiv cu rezultate aproximative; 2) Aria şi formulele de calcul pentru figurile de bază (triunghiuri şi patrulatere); 3) Teorema lui Pitagora (demonstrată prin arii) cu calcule pe două nivele: la început cu rezultate exacte, pe baza tripletelor pitagorice, iar apoi cu rezultate ne-exacte, calculate aproximativ. Aici ajungem să exersăm cu sens extragerea aproximativă a rădăcinii pătrate. De-abia în semestrul II introduc noţiunea de număr iraţional, prezint scoaterea de sub radical, facem primele calcule algebrice cu numere iraţionale şi reluăm probleme cu calcul de arii şi perimetre prin teorema lui Pitagora, dar unde dăm rezultate iraţionale exacte.

Consider că aceste propuneri ar fi parte activă a unei forme de matematică naivă potrivită, adaptată vârstei gimnaziale, prin care elevii să urce liniştit, treptat către nivelele intelectuale necesare promovării cu succes a examenului de Evaluare Naţională de la sfârşitul clasei a VIII-a.

18 iulie 2016

Prof.C. Titus Grigorovici

Vezi și: Matematica naivă

Kassel-8 din 20 martie 2016

Matematica începe la pragul către lumea spirituală (Mathematik beginnt an der Schwelle zur geistigen Welt – Mathematics Begins at the Threshold of the Spiritual World)

În perioada 18 – 24 martie 2016 a avut loc la Kassel, în centrul Germaniei, al optulea curs de formare pentru profesorii de liceu din şcolile Waldorf. În fiecare an acest curs se concentrează asupra unei clase, anul acesta atenţia principală fiind îndreptată spre diferitele materii ale clasei a IX-a. Conferinţa celei de-a treia zi a fost despre matematică, fiind ţinută de către dl. Detlef Hardorp, german având şi cetăţenie americană, un personaj deosebit cu un PhD. la Princeton. În rândurile următoare voi încerca să prezint câteva idei din discursul foarte încărcat şi rapid al d-lui Hardorp.

Prelegerea a început cu o iluzie optică, o imagine iluzorie care ne convingea să vedem un triunghi, deşi pe ecran erau poiectate doar mai multe forme ce încadrau o zonă triunghiulară; astfel, eu privesc în lume şi există diferite feluri de a privi. Noi figurăm, ne imaginăm spaţiul (We figure the space): cu ochii “pipăim” mediul înconjurător. Jean Piaget vorbea de percepţia spaţială a copilului, care ar trebui să se fi dezvoltat până la 13 ani. Percepţia spaţială este una imaginară: noi “strălucim/radiem plasticitate” în spaţiu, pentru că voinţa intervine în vedere. Piaget amintea că înţelegerea nodurilor are loc pe la 13 ani.

Matematica nu există senzorial, ea este pur suprasenzorial. Astfel, Rudolf Steiner a explicat încă în 1920: Matematica este prima treaptă a privirii suprasenzoriale.

Numărul este un element ritmic. În cartea sa Omul care îşi confunda soţia cu o pălărie (în traducere în română la Ed. Humanitas, 2011), Oliver Sacks vorbeşte despre dereglarea simţului mişcării; cu simţurile proiectate în afară apare sentimentul matematic. Rudolf Steiner spunea că structurile matematice plutesc deasupra lumii senzoriale. Acestea se referă la elemente din lumea senzorială, dar nu sunt legate senzorial. Eu gândesc despre ceva senzorial, nu gândesc senzorial. Matematica este suprasenzorială, dar trebuie să ai un nivel dezvoltat de simţire pentru a putea gândi adevărul matematic.

Cel mai înalt caracter al matematicii este frumuseţea, care este dincolo de prag, şi care ne aduce sentimente de fericire. În matematică apare libertatea de a gândi; poţi creea lumi noi. La matematică trebuie să începi să gândeşti, chiar dacă gândeşti greşit; să gândeşti fără ruşine. Dacă dezvolţi ruşine, atunci ai încheiat-o cu matematica (de exemplu, învăţând doar calculul schematic). Oarecum, matematica aplicată doar ca un cumul de reţete este o adevărată otravă pentru gândire. De fapt, matematica nu poate fi explicată cu adevărat. Profesorii pot doar să le ofere elevilor oportunităţi de a avea trăiri de uimire, trăiri “AHA!”. În acest sens, curriculumul este foarte important, dar metodica şi didactica sunt mult mai importante. Arta de predare a profesorului constă în a lăsa activitatea elevului, mai ales în predarea matematicii. Altfel obţinem doar calcul schematizat, iar calculul schematizat neînţeles reprezintă otravă pentru gândire.

În continuare dl. Detlef Hardorp a explicat că avem nevoie de o pedagogie care lucrează cu intuiţia. Matematica creşte doar dacă procesul de gândire este voit. George Polya spunea că trebuie să ajungem cu elevii să facă gesturi plauzibile; de exemplu să construiască ei combinatorica (în româneşte avem pentru asta denumirea de problematizare, iar Eugen Rusu o denumea mai amplu matematica proces, spre deosebire de matematica rezultat reprezentând doar predarea de reţete – comentariu CTG). Frumuseţea la combinatorică este că aceasta poate fi dezvoltată/cucerită prin gândire pură (o formă total diferită de cea din manualele româneşti – comentariu CTG). Ţelul este ca fiecare elev să participe la procesul de gândire. Dacă le ceri elevilor să aplice formule, s-ar putea ca să nu ştie care formulă să o aplice. Trebuie neapărat ţinută trează gândirea, iar aceasta se poate face minunat la combinatorică.

În final, dl. Hardorp s-a referit şi la Gândirea dialogică a lui Peter Gallin (vezi postarea din oct. 2015 – comentariu CTG), predare în care acesta colectează feedback-ul gândirii elevilor, iar în urma acestora aste decis următorul pas. Astfel, curriculumul vine de la elevi! (cine voia proiecte inovative de predare? 🙂 – comentariu CTG). Astfel, Peter Gallin previne avarierea matematică a elevilor.

Producerea cunoştiinţelor matematice este mai uşoară decât reproducerea acestora, pentru că la receptare trebuie gestionate două puncte de vedere (al profesorului care predă şi al elevului care preia). Din acest motiv învăţarea trebuie începută cu producerea (un singur punct de vedere, cel al elevului care se străduieşte să producă – comentarii CTG). Calculul schematic poate fi folosit fără a dăuna doar dacă, în prealabil, schemele şi formulele au fost produse de către elev prin propria gândire.

1 iulie 2016

Titus Grigorovici

Geometria sferei în sprijinul geografiei; Corpuri de rotaţie

După parcurgerea lecţiei despre sferă mi-am permis ora următoare un “20 minute” de studiu al unor elemente de geografie şi astronomie legate de geometria sferei. Elevii le cunosc teoretic, dar din păcate cunoştinţele de geometrie ale profesorilor de geografie nu acoperă întotdeauna toate fineţurile de gândire ale fenomenului, astfel încât de multe ori aceste cunoştinţe ajung să fie doar învăţate pe de rost, fără a fi şi înţelese. Şi în nici un caz profesorul de geografie nu va merge la clasă cu compasul şi cu raportorul pentru a face un desen cât mai corect pe tablă.

În a doua parte a orei am oferit elevilor nişte probleme cu corpuri de rotaţie. Acestea nu mai sunt în programă cam de un sfert de secol, dar eu consider că sunt foarte clare, conţinând o matematică vie, plină de gândire accesibilă elevilor de a VIII-a şi care chiar le aduce bucurie prin satisfacţia rezolvării, acestea nefiind prea banale. Măcar aceste trei probleme ar trebui să le parcurgă orice elev, dar se mai pot face şi altele. Pe tablă găsiţi doar problemele; rezolvările sunt la elevi în caiete :-).

Titus Grigorovici

Sfera şi bila

Lecţia despre sferă/bilă cu aria şi volumul acestora conţine demonstraţii legendare, ce pot oferi o mare satisfacţie elevilor buni de clasa a VIII-a. Nu mi-am propus pentru această postare să prezint în detaliu toată lecţia, dar mă gândesc să va descriu puţin cele două poveşti cu care pregătesc calcului volumului, respectiv al ariei, înainte de a vă lăsa să vedeţi lecţia de pe tablă.

Pentru volum – ciudat, dar se începe cu demonstrarea formulei volumului – se construieşte un corp interesant, un cilindru cu secţiunea axială pătrată, de aceeaşi rază cu sfera, din care se scot două conuride la cele două baze, conurile având vârful comun în “centrul” cilindrului. Eu le descriu elevilor acest corp, comparându-l cu o conservă de pateu căreia i-am scos ambele capace şi din care am extras cele două conuri de pateu cu un cuţit cu vârf. Ideea este de a arăta că volumul pateului rămas este egal cu volumul bilei, arătând aceasta prin faptul că la orice înălţime secţionăm cele două corpuri, ariile secţiunilor vor fi egale. Partea de calcul a demonstraţiei este simplă şi percutantă: nici nu-ţi dai seama bine cum ai pornit şi este deja gata.

Pentru demonstrarea formulei de arie le povestesc elevilor despre un vânzător de pepeni care are un pepene perfect sferic şi un cuţit cu care taie bucăţi de degustat. Cuţitul are lama de lungime exact cât raza pepenelui iar bucata oferită spre degustare, cu vârful exact în centru, are forma unei piramide cu baza de coajă (puţin bombată). Apoi ne imaginăm că acest vânzător de pepeni îşi propune să tot taie bicăţi pentru degustare cât mai înguste (pentru a evita baze bombate), deci cât mai multe, şi le aranjează pe masă, toate cu vârful în sus şi aşa mai departe. De aici încolo fiecare se poate descurca cu povestea şi cu trecerea acesteia în demonstraţie şi în calculul pentru obţinerea formulei.

După ce avem formulele fac câteva exerciţii mai mult orale de calcul a ariei şi a volumului unei semibile şi a unui sfert de bilă (merge uşor şi optimea de bilă). Spor la lecţie de pe tablă.

Titus Grigorovici

Conul circular drept

Sărim peste lecţia despre cilindrul circular drept, pentru că aceasta este una din cele mai simple lecţii de clasa a VIII-a. Plecând de la premiză că profesorul chiar se străduieşte, el va reuşi o lecţie foarte bună, elevii implicându-se şi putând ajuta cu adevărat. Toţi au văzut până acum conserve, chiar au desprins eticheta de pe o butelie de Cola, aşa că vor înţelege foarte bine aria laterală (eu chiar desenez desfăşurarea suprafeţei laterale sub formă de dreptunghi care “se mai ţine un pic de cilindrul desenat”). La volum, principiul “aria bazei înmulţit cu înălţimea” se poate discuta foarte bine pe baza pachetelor de biscuiţi rotunzi: Câtă cantitate este în pachet? Păi, cântăresc un biscuite şi număr câţi biscuiţi sunt în pachet.

Mai deosebită este lecţia următoare, despre conul circular drept. Volumul acestuia nu generează mari probleme; elevii înţeleg analogia cu volumul piramidei. Foarte interesantă este însă, şi merită lucrată cu răbdare, deducerea formulei pentru aria laterală a conului. Eu predau elevilor exact lecţia pe care am primit-o în clasa a VIII-a de la profesorul meu Wilhelm Schoch, lecţie ce m-a impresionat profund şi cu ajutorul căreia am putut oricând să-mi re-deduc formula în cap.

De fiecare dată când predau această lecţie cu împărţirea sectorului de cerc în foarte multe “triunghiuri tare înguste” nutresc speranţa că sădesc în mintea elevilor o sămânţă pentru o evoluţie frumoasă în liceu la calcului diferenţial şi integral.

O tehnică similară se foloseşte şi la găsirea formulei pentru aria laterală a trunchiului de con circular drept, doar că suprafaţa laterală desfăşurată (un sector de inel circular) se descompune într-o sumă de “trapeze” foarte înguste. Calculul merge similar şi, fiind la a doua întâlnire, le place foarte mult elevilor.

Iată în continuare pozele tablei de la lecţia despre conul circular drept.

Titus Grigorovici