(amintiri matematice din copilărie)
Iarna este anotimpul şezătorilor. Stând împreună cu cei dragi ne cuprinde nostalgia şi începem să depănăm amintiri. Vă invit să finalizăm depănarea amintirilor mele matematice de învăţăcel cu anii de facultate petrecuţi la Cluj, completate şi cu alte amintiri matematice din copilărie.
Prof. Constantin Titus Grigorovici
*
Facultatea
La examenul de admitere la facultatea clujeană am constatat în mod dureros că aveam nevoie de ochelari. Fusesem repartizat cam la jumătatea amfiteatrului unde s-a desfăşurat examenul, fiind astfel destul de departe de tablă. Până atunci, de prin clasa a VI-a ocupasem întotdeauna unul din locurile laterale din prima bancă (lângă uşă sau lângă geam, pentru a nu încurca colegii). Trebuie precizat că la vremea respectivă subiectele erau scrise de către profesor pe tablă, iar noi trebuia mai întăi să le copiem. Ei bine, la examenul de analiză matematică, la o funcţie, în loc de x2 am copiat xx, dându-mi peste cap toate calculele din acea problemă.
Primul lucru interesant legat de facultatea de matematică este faptul că ne-am găsit patru colegi ai căror părinţi fuseseră şi ei colegi ai acestei facultăţi, absolvenţi în 1965. La trei dintre cei patru chiar ambi părinţi fuseseră colegi în respectiva promoţie. Cu doi dintre colegii mei s-a format chiar o relaţie asemănătoare cu cea de rude: ne simţeam ca un fel de verişori, când ne întâlneam cu părinţii vre-unuia discutam de cei absenţi şi se transmiteau salutări; părinţii tocmai avuseră întâlnirea de 20 de ani de la terminarea faculţăţii. Şi acum suntem cu aceştia la fel de apropiaţi ca şi cu rudele adevărate.
Din timpul facultăţii nu am nici o amintire legată de subiectul prezentului eseu, demnă de a fi prezentată aici. Matematica din facultate nu semăna deloc cu ce văzusem eu şi nu prea m-a atras. Totuşi, au fost destule momente deosebite. De pildă, renumita formulă a lui Euler ce a apărut din senin într-un curs: eiπ = –1 şi care nouă ne plăcea mai mult în forma eiπ + 1 = 0, pentru că aşa conţinea într-adevăr toate numerele remarcabile din matematică. De curând am aflat dintr-o carte a Profesorului Ian Stewart că, din când în când se fac sondaje printre matematicieni despre care ar fi cea mai frumoasă formulă matematică – ne vine sau nu să credem, dar există şi aşa ceva, dânsul ne asigură că n-a inventat acest fapt – şi că de obicei câştigă renumita formulă a lui Euler (Professor Stewarts Mathematisches Sammelsurium, Ed. Rewohlt T. Verlag, 2011, pag.230). În rest, din timpul facultăţii am rămas în suflet cu multe imagini model ale profesorilor, imagini care mi-au oferit o linie ghidantă sănătoasă în viaţă.
De-abia la sfârşitul facultăţii s-a petrecut din nou ceva cu adevărat deosebit: în timpul unei ore când nu se întâmpla nimic special (doar ceva analiză complexă cu legendarul Profesor Petru Mocanu), m-am gândit că n-am mai descoperit nimic de vreo şapte ani. Mama prezenta în continuare formula mea de arie a triunghiurilor în fiecare an, şi atâta vreme cât în liceu mai erau generaţii care ne cunoşteau, pe mine sau pe fratele meu, din când în când apărea în câte o demonstraţie la teză sau la o lucrare scrisă: „folosind teorema lui Titus …”. Mama era foarte mândră şi mă mai anunţa şi pe mine când se întâmpla aşa ceva. Din păcate nu am păstrat nici măcar una din acele probleme sau demonstraţii.
Dacă vroiam să mai descopăr ceva, aveam nevoie înainte de toate de o întrebare pe care n-a mai pus-o nimeni până atunci. În acea oră de mai, în cca. 10-15 minute am avut întrebarea; în două ore am găsit răspunsul; peste patru ani aveam o demonstraţie credibilă şi prezentam rezultatul la sesiunea de comunicări ştiinţifice pentru profesori Didactica Matematicii (exact în ziua în care soţia mea a venit acasă cu fiul nostru de la maternitate :-). Peste încă opt ani, în urma impulsului dat de către un alt fost profesor din facultate, reuşeam să găsesc continuarea într-un întreg complet. Toată teoria este prezentată în cele două articole în serie din Caietele Pentagonia Nr. 7 şi 8 – Reprezentarea conicelor în spaţiu complex (de găsit pe site-ul pentagonia.ro – Arta predării matematicii). Reuşisem să merg din nou cu mintea pe unde n-a mai „călcat” gând de om. Dar de data aceasta nu din întâmplare, în urma unor stimulări conjuncturale, ci din proprie inţiativă, iar apoi chiar la o cerere venită din exterior.
Viaţa de profesor şi reactivarea unor amintiri matematice
Deşi am terminat facultatea în 1989, datorită armatei de 6 luni am început să predau la clasă doar în primăvara lui 1990. Toate cele prezentate până aici sunt amintiri matematice ce nu s-au şters şi cu care am ajuns în viaţa de adult. Unele poate s-ar fi şters dacă nu aş fi ajuns profesor, aşa cum se întâmplă la cei mai mulţi oameni.
Mai există însă o categorie specială de amintiri matematice din timpul şcolii, anume cele care s-au şters, dar au fost reactivate, readuse din uitarea în care s-au scurs cu timpul, ele neînsemnând la momentul respectiv nimic special, nefiind legate de vre-o întâmplare deosebită, ci intrând în cursul natural al lecţiilor care se uită pentru că vin tot altele peste ele. În cazul meu astfel de amintiri, adică anumite cunoştinţe matematice, au fost reactivate prin însemnătatea lor în procesul de predare, observându-le necesitatea în educarea matematică a generaţiilor de elevi.
Probabil cel mai bun exemplu în acest sens îl reprezintă forfecarea triunghiurilor şi a paralelogramelor. La triunghiuri această denumire înseamnă faptul că aria unui triunghi nu se modifică dacă vârful său este translatat paralel cu baza, adică dacă un vârf alunecă pe o dreaptă paralelă cu latura opusă, obţinându-se astfel un triunghi de altă formă faţă de cel iniţial, dar echivalent cu acesta. Aceaşi proprietate se regăseşte la paralelograme dacă translatăm o latură pe dreapta sa suport.
Cu aceste proprietăţi se pot rezolva anumite probleme într-un mod foarte elegant, realizănd cu figurile geometrice un proces de mişcare ce aminteşte de un balet deosebit şi care transformă figurile într-un mod foarte sculptural, amintind uneori de picturile lui Kandinski (cu puţină imaginaţie s-ar putea ajunge la compararea acestora cu stilul de mişcări de scenă dezvoltat de Michael Jackson). Pentru noi, soţia mea şi cu mine, ele reprezentau însă o normalitate şi le scoteam din recuzita de metode atunci când aveam nevoie de ele şi atât.
Aceste proprietăţi reprezintă însă un punct de mare interes în metodica predării matematicii în pedagogia Waldorf, prin faptul că ne oferă un proces în mişcare. Or, în pedagogia Waldorf se recunoaşte şi se respectă faptul că elevul înţelege şi învaţă mult mai bine matematica prin mişcare – atât mişcare exterioară, fizică, în clasele mici, cât şi mişcare interioară, imaginativă, în clasele mari. Cu forfecarea paralelogramelor se poate demonstra Teorema lui Pitagora, aceasta fiind demonstraţia folosită de obicei în şcolile Waldorf din vestul Europei.
Teorema lui Pitagora poate fi demonstrată însă şi cu forfecarea triunghiurilor, drumul fiind asemănător (o forfecare de triunghi, urmată de o rotaţie, iar apoi din nou o forfecare). Figura acestei demonstraţii o văd regulat pe coperta la Culegerea cu Teste grilă de matematică pentru Admiterea din 2013 de la Universitatea Tehnică din Cluj (Editura UTPRESS, o carte fără pic de geometrie sintetică, dar plină de geometrie analitică, matrici, funcţii, limite şi tot soiu’ de integrale de chinuit doritorii), deci mă gândesc că este privită ca o figură clasică a matematicii.
Din păcate însă, această figură nu se mai face în şcoli; în cursurile de pedagogie Waldorf am avut neplăcuta surpriză să văd că profesorii colegi mai tineri nu cunosc această demonstraţie, în general nu cunosc demonstraţiile în mişcare prin forfecare, deci nici problemele corespunzătoare. Doi dintre ei mi-au povestit cum, odată la un curs desfăşurat în străinătate, profesorul care ţinea cursul i-a încuiat pe toţi participanţii cerându-le să dea măcar două-trei demonstraţii la Teorema lui Pitagora. De ce n-am fost eu acolo să le povestesc despre pictura murală a lui tata din copilărie?
Aceste amintiri din copilărie mi-au fost readuse în actualitate de către profesorii docenţi la ale căror cursuri am participat ca profesor în şcoala Waldorf, în România respectivele lecţii fiind de mult uitate. Există însă şi amintiri din copilărie ce au revenit într-un mod misterios şi enigmatic, fără a fi ajutate de către cineva. De pildă, în 2000 am avut un moment de inspiraţie şi am organizat lecţia despre arii din clasa a VII-a într-un anumit fel. Peste câţiva ani am constatat cu surprindere că lecţia respectivă avea exact forma găsită de mine şi în manualul de clasa a V-a al profesorului Eugen Rusu, după care am învăţat eu în copilărie, regăsit “în lada de cărţi vechi” la părinţii mei.
Alt set de amintiri matematice din copilărie
O sumedenie din amintirile ce le am din perioada şcolară le-am regăsit şi la soţia mea, Mariana, fapt ce îmi dă convingerea că multă lume are astfel de amintiri, într-un mod similar. De pildă, atât eu din Victoria, cât şi ea din Cluj, ne amintim din copilărie cum stabileau vânzătoarele preţul, la Alimentara. Ne trimiteau mama fiecăruia să cumpărăm “200 g” de salam: vânzătoarea tăia o bucată aproximatovă din salamul cerut, îl punea pe o hârtie pe cântar, care arăta să zicem 220 g, iar vânzătoarea calcula imediat preţul în cap. Când eram copii eram uimiţi de rapiditatea de calcul a vânzătoarelor. Până acasă tot calculam şî de fiecare dată constatam că avusese dreptate. După ’90 am fost uimiţi cum breasla vânzătorilor a uitat încet această abilitate.
Amândoi avem din copilărie câte o culegere Gheba, a mea pe germană ,a ei pe română, care arată acum ciudat de asemănător: culegerile groase cam de 2 cm prezintă o distrugere pronunţată a primelor cca. 30 de pagini, a mea fiind folosită intens de doi fraţi, a ei şi mai distrusă fiind folosită de trei fraţi. În acest sens se vede că din culegerile Gheba se lucra intens doar partea de exerciţii de aritmetică şi de algebră; partea de geometrie nu se arată la nici una dintre culegeri prea folosită.
Evident că şi amintirile despre Gazeta Matematică sunt asemănătoare. Am lucrat amândoi după aceleaşi manuale, preţuim la fel de mult construcţiile geometrice cu rigla şi compasul etc.
Desigur că există şi multe amintiri diferite. Să începem cu profesorii. În clasele V-VI Mariana a făcut matematică cu o persoană legendară în Cluj, profesorul Dumitru Bota. Legat de acesta, pe lângă admiraţia cu care vorbea soţia mea despre el, există două amintiri speciale.
Profesori fiind, la o discuţie despre ce şi cum să facem cu elevii, soţia mea şi-a amintit că la Bota scria foarte mult la teme şi nu ne puteam închipui ce anume scria atâta. Aşa că l-a întrebat pe tatăl ei; iată şi răspunsul dat de socrul meu: trebuia să copieze fiecare lecţie de la clasă în caietul de teme şi de-abia apoi făcea şi tema propriuzisă.
O a doua amintire vine din clasa a VI-a, de la geometrie. Povesteşte soţia mea că Bota desena nişte cercuri impecabile cu mâna liberă, şi ei elevii erau de fiecare dată uimiţi. La un moment dat profesorul şi-a rupt mâna dreaptă, cu care scria. Când a venit la şcoală, cu mâna în ghips, a ţinut lecţia scriind cu mâna stângă pe tablă. Iar când a fost nevoie de un cerc, Bota pur şi simplu a trasat cu stânga un cerc aproape perfect, lăsându-i pe toţi cu gura căscată. Şi de la alte persoane am auzit poveşti pline de admiraţie despre acest profesor.
Din păcate în clasa a VII-a s-a schimbat profesorul, venind o doamnă despre care soţia mea nu are deloc amintiri plăcute. Se pare că nu stăpânea prea bine predarea, iar Mariana o tot corecta, aşa că prin a VIII-a a dat-o afară de la ore, cerându-i să nu mai vină la mate.
În clasa a VIII-a a mers la olimpiadă până la faza judeţeană, care era cea mai înaltă posibil în acele vremuri. Aici a greşit, uitând că cel mai mic multiplu al unui număr este zero, ratând astfel un exerciţiu, fapt pentru care nu a ieşit pe locul 1 pe judeţul Cluj.
În liceu a avut o altă legendă la mate, pe profesorul Ambrozie Lelijak. Sunt multe amintiri din aceşti ani de la orele de matematică. De pildă felul în care acesta dădea tezele sau cum îsi notau “dumele” sale în caiet atunci când făcea haz de vre-un coleg care nu învăţase; caietele tuturor colegilor erau pline la spate cu citate din Lelijak.
Amintiri din copilăria matematică a părinţilor
Discutând mult despre matematică şi cum ar trebui predată aceasta, ajung uneori şi părinţii noştri să-şi amintească scene din copilărie legată de acest subiect. De pildă mama mea şi-a amintit odată cum a lăudat-o directorul şcolii din sat. Acesta era soţul învăţătoarei şi îi plăcea să vină în asistenţe la ore. Cu astfel de ocazii a remarcat-o cât de bine ştia ea la problemele de aritmetică, chiar din acelea aduse de el, cele “mai tari” şi cum le făcea pur şi simplu fără să-i fi dat vreo explicaţie preliminară. Prin 2000, era şi mama deja pensionată, s-a întâlnit cu directorul din copilărie şi acesta şi-a amintit cum dădea ea cele mai neobişnuite rezolvări, cu care ajungea însă la răspunsul corect.
Acest aspect l-au sesizat ulterior la ea şi profesori de matematică din şcoală şi din liceu. Aceştia o îndrăgeau şi o ajutau cum se putea în acei ani cu colectivizare forţată, mama provenind dintr-o familie simplă de la ţară; de pildă, mi-a povestit că primea gratuit abonament la Gazeta Matematică. Peste ani, când a intrat la facultate, bunicul ei a vândut un viţel pentru a-i da bani să aibă la şcoală la Cluj.
Tata era dintr-o familie intelectuală, bunicul terminând două facultăţi: Ştiinţele naturii la Cernăuţi şi, în timpul războiului, Dreptul la Iaşi. Tata îşi aduce aminte de profesorul de matematică din liceu, dl. Lungu Nicolae, absolvent de facultate la Iasi, cum acesta le dădea la începutul orei câte trei probleme cu care “să-şi bată creierii”, până le verifica dânsul temele. Apoi, pe parcursul lecţiei noi, elevii observau cu uimire că problemele iniţiale se rezolvau uşor cu lucrurile nou învăţate şi mare le era bucuria despre cele descoperite. Asta da modalitate de predare prin problematizare dusă la extrem!
De la tata mai există o poveste cu final dureros. Prietenul său cel mai bun Cojocaru Dragos, cu care au fost colegi şi în facultate, s-a calificat în liceu, la prima Olimpiadă Naţională organizată la matematică, pe locul I din partea judeţului Suceava. După o vreme şi-au dat seama că a fost înlocuit şi Dragoş nu a mai fost convocat la faza finală. Peste ani, în 1984 eram împreună cu tata într-o tabără de matematică la Câmpulung Moldovenesc, tata fiind însoţitorul grupului de olimpici (rezerve) din judeţul Braşov. Cu această ocazie tatăl meu s-a interesat de la colegii organizatori suceveni despre profesorul lui din liceu şi a aflat că acesta este la cel mi bun liceu din Suceava, că este deosebit de apreciat, dar că – nimeni nu înţelege de ce – nu participă nici o dată la olimpiade.
Şi de la tatăl soţiei, inginerul Dodul Eugen (se pronunţă Dodu’) avem câteva amintiri depănate de-a lungul anilor. Născut în 1929 la Chişinău, a fost refugiat cu familia în timpul războiului la Bucureşti, unde până la urmă au şi rămas. La început, la şcoală nimeni nu-l înţelegea, având o pronunţie mult diferită faţă de ceilalţi colegi. Astfel, şi-a salvat onarea în faţa colegilor la orele de limba franceză, pe care o ştia de acasă, şi în matematică la care era foarte bun.
Anii au trecut şi în liceu ajunsese un fervent rezolvitor la Gazeta matematică. La sfârşitul şcolii ajunsese pe locul doi pe ţară la punctajul concursului rezolvitorilor din GM, primul fiind prietenul său. Ne putem închipui supărarea trăită atunci când colecţia sa de Gazete Matematice a fost atacată de carii, astfel încât valoroasele caiete au trebuit arse. Peste ani a găsit printr-un anticariat câteva gazete vechi din anii liceului: le-a legat pe toate opt exemplarele într-un mic volum în care se găsesc câteva semne în dreptul paginilor pe care este trecut numele său, din clasele VI-VII de liceu (Gazeta Matematică, Supliment de exerciţii, Anul XII-XIII, 1946).
La admiterea în facultate a ratat ultimul examen din trei prin neprezentare, datorită faptului că a stat toată noaptea şi a citit Anna Karenina. Nici nu s-a dus apoi să vadă rezultatul, convins fiind că nu a intrat, dar a aflat în toamnă de la un coleg al său că este student şi că profesorii îl trec regulat absent.
Mai târziu, inginer constructor fiind, peste tot pe unde umbla pe şantierele ţării, medita la matematică copii colegilor de servici. Când am cunoscut-o pe Mariana, tatăl ei avea săptămânal ore private cu 30 de elevi; atâţia erau că nu le putea ţine socoteala la toţi, aşa că îşi făcuse catalog unde nota cum îşi fac aceştia temele şi cum progresează.



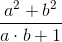 este pătratul unui număr întreg. În textul original observăm că se foloseşte denumirea întreg pozitiv pentru număr natural.
este pătratul unui număr întreg. În textul original observăm că se foloseşte denumirea întreg pozitiv pentru număr natural.