În prima postare despre Criteriul psihologic al intuiţiei în selectarea teoremelor de demonstrat, publicată la începutul lui 2018, vorbeam despre Suma unghiurilor exterioare ale unui triunghi sau ale unui patrulater. Această serie de teoreme neinclusă în programa oficială este surprinzătoare prin faptul că rezultatul este întotdeauna 360o (se păstrează şi la orice alt poligon), pe când suma unghiurilor interioare variază, adăugând câte 180o la fiecare latură în plus.
Teoremele pot fi prezentate “pentru pretenţioşi” şi într-una singură, dar eu recomand eşalonarea acestora în trei etape, în paralel cu evoluţia gândirii elevului, mizând în fiecare pas pe surprinderea elevului, dar şi pe faptul că de la un moment la celălalt aceştia evoluează iar subconştientul lor lucrează. Prezentarea unei singure teoreme la lecţia despre poligoane în clasa a VII-a ar dezvălui întregul fenomen de-o dată, eliminând factorul temporal şi evoluţia gândirii copilului din discuţie. Aceasta ar fi o predare curat matematică, pe când eu pledez pentru o predare mai artistică, ca într-un film ce nu-ţi dezvăluie dintr-o mişcare totul, ci îţi eşalonează informaţiile până spre final, personajele evoluând cu timpul (la fel şi în forma propusă de mine, unde informaţiile evoluează).
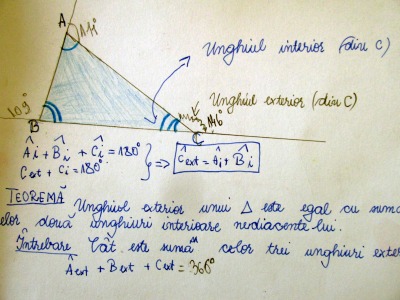
Concret, eu nu am făcut la clasă suma unghiurilor exterioare, ci am dat-o ca temă, discutând-o apoi la începutul orei următoare. Din temele elevilor am ales o serie de imagini care arată şi diferitele tipuri de gândire, conform nivelului de evoluţie al gândirii elevului. Astfel, Elevul 1 are clar o gândire concretă, o gândire în stadiul operaţional concret (gândire specifică copiilor): el a măsurat cele trei unghiuri exterioare şi a calculat suma. Evident că a înţeles ce sunt acelea unghiuri exterioare şi mânuieşte corect şi exact raportorul.
Elevul 2 s-a gândit că ar trebui să aplice teorema învăţată la clasă, dar gândirea sa este încă concretă la bază. Elevul 3 este trecut de mult într-o etapă nouă de gândire, cea specifică stadiului operaţional formal (nivelul adult de gândire) El nu a mai măsurat nimic, ci doar a aplicat sec teoremele învăţate înainte, dovedind că stăpâneşte inclusiv gândirea algebrică necesară unui astfel de calcul. Se vede că elevul 2 este situat în procesul evoluţiei gândirii într-o poziţie intermediară, de tranziţie, între gândirea concretă şi cea formală (trecerea de la o fază la cealaltă a gândirii se face – teoretic – undeva între 11 şi 12 ani, existând însă şi excepţii în ambele sensuri). După verificarea temei le-am arătat elevilor şi o demonstraţie de tipul celei cunoscute de la suma unghiurilor interioare în triunghi.
Când am trecut la patrulatere, după prima lecţie unde studiasem suma unghiurilor (interioare), le-am dat din nou ca temă găsirea sumei unghiurilor exterioare. Elevii tocmai au văzut că suma unghiurilor interioare s-a dublat (aşa văd elevii în acel moment; că se adaugă de fapt încă 180o odată cu adăugarea unei laturi, asta vor descoperii de-abia la studiul poligoanelor cu mai multe laturi). De vreme ce suma unghiurilor interioare s-a dublat, este de aşteptat să se modifice rezultatul şi la suma unghiurilor exterioare, dar, surpriză (acasă, la făcutul temei, pentru cei care au forţa), suma unghiurilor exterioare se păstrează la fel ca la triunghiuri. Între timp tehnica de calcul a mai evoluat, există şi ştersături, poate a mai ajutat şi o verişoară dintr-o clasă mai mare (?), dar oricum, iată că răspunsul este tot 360o (ultima imagine).
La poligoanele regulate voi da din nou această temă şi ne putem închipui cum vor fi rezolvările şi discuţiile de la clasă (poate vor fi elevi care vor zice direct la datul temei că rezultatul trebuie să fie tot 360o). ctg



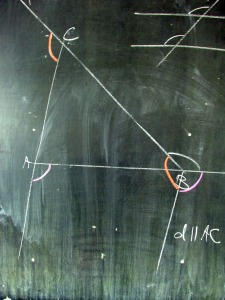

Părerea mea este că la triunghi avem 6 unghiuri exterioare( 2 câte 2 congruente) , la patrulater la fel. Când calculăm suma unghiurilor exterioare, nu le luam pe toate?