La începutul lunii aprilie am fost atenţionat asupra unui articol de pe edupedu.ro; doar în urma unei scurte priviri asupra acestuia (mai puţin decât o lectură “pe diagonală”); mi-am dat însă atunci seama despre ce este vorba şi, considerându-l valoros, m-am grăbit să-i fac publicitate. Fiind foarte ocupat, nu am apucat să-l citesc în detaliu, decât peste o săptămână, după intrarea în vacanţa de Paşte. Toate ideile cuprinse în precedentul eseu – O analiză (1) – reprezintă gânduri stârnite doar de această primă şi scurtă privire asupra articolului respectic, mai mult însă a indignării în urma comentariilor văzute în final (când mai aveam scurte momente libere mintea îmi fugea tot la aceste aspecte). Precedenta primă parte a analizei se bazează pe acele gânduri. Păstrând spectrul ideilor, înainte de a trece la a doua parte, doresc să vă ofer următorul:
A.S. (ante scriptum) În paralel cu munca la această dublă analiză mă mai gândeam şi la o continuare a seriei (brusc întrerupte) despre ideile găsite în prefaţa culegerii din 1982 a Profesorului A. Hollinger, când – Surpriză! – spre finalul acelui text găsesc o trimitere la un mic set de trei demonstraţii prin arii la teorema lui Pitagora (în cadrul paragrafului 10.4 Demonstraţii bazate pe arii, pag. 95). Prima din cele trei “probleme” este următoarea:
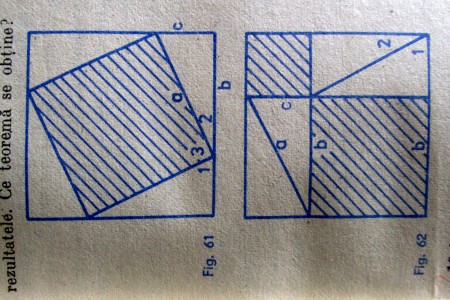
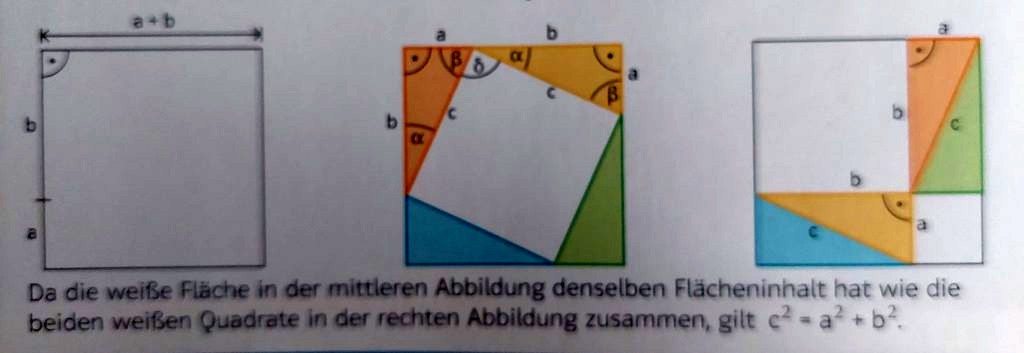
10.4.4. Fie b şi c catetele şi a ipotenuza unui triunghi dreptunghic. Se construiesc un pătrat cu latura b + c şi patru triunghiuri congruente cu triunghiul dat, aşezate ca în figura 61. Apoi se construiesc patru triunghiuri congruente cu triunghiul dat, aşezate ca în figura 62. Să se calculeze aria părţii din pătrat care rămâne neacoperită de triunghiuri şi să se compare rezultatele. Ce teoremă se obţine? (din motive tehnice am aşezat poza culcat)
Acest exemplu vine “la ţanc” pentru cei care ar considera disputa iscată de articolul iniţial ca fiind una între “matematica lor, a celor din vest” şi “matematica noastră”. Nici vorbă de aşa ceva. Textul şi pozele de mai sus sunt luate din culegerea profesorului A. Hollinger, Probleme de geometrie pentru clasele VI-VIII, Ed. Didactică şi Pedagogică, 1982. Nu am la îndemână manualele dânsului, însă bănuiesc că demonstraţia respectivă se găseşte şi acolo.
Dar să revenim la analiza noastră. Pe când începusem să lucrez la redactarea acesteia am văzut că de fapt articolul era preluat de pe blogul CEAE – Centrul de evaluare şi analize educaţionale (iată adresa articolului iniţial: https://ceae.ro/cum-este-demonstrata-teorema-lui-pitagora-intr-un-manual-german-de-matematica-o-comparatie-cu-romania/ ). Lecturându-l cu mai apăsată atenţie, am găsit multe aspecte noi ce ar merita discutate. În acest sens permiteţi-mi să reiau integral articolul respectiv, dar să-l întrerup din când în când cu comentariile şi accentuările mele personale (citatele din articolul CEAE sunt scrise înclinat, iar comentariile mele intercalate neînclinat).
*
Cum este demonstrată Teorema lui Pitagora într-un manual german de matematică. O comparație cu România
Îmi exprimam părerea în prima parte a analizei că ar fi de evitat astfel de comparaţii (chiar din titlu), care pot stârni ego-ul în sufletul unor colegi. Din acest motiv, discuţia ar trebui să se mute din zona “nemţii au cele mai bune maşini şi cele mai tari autostrăzi, dar noi avem cea mai tare matematică din lume”, într-o zonă mai pragmatică pentru noi, anume în zona argumentelor psihopedagogice, în zona nevoilor şi a posibilităţilor fiecărei vârste şcolare, de fapt într-o zonă metodico-didactică realistă. Pura întâmplare m-a ajutat să pot face repede divagaţia spre americani, dar de fapt noi ar trebui să ieşim din starea de a lua lucrurile de-a gata de la străini (alteori ne apucă cu finlandezi sau cu britanicii etc.), şi să începem să decidem raţional ce este nevoie cu adevărat pentru a vindeca predarea matematicii în şcolile româneşti (mai ales în ciclul gimnazial, unde materia este obligatorie pentru toţi elevii, neselectaţi oficial; astfel, noi ar trebui să punem un mai mare accent pe satisfacerea în mod echilibrat a nevoilor tuturor categoriilor de elevi). Asta nu înseamnă să nu ne uităm la ce fac ceilalţi, pentru că şi de acolo ne pot veni idei bune: ne uităm şi la unii şi la alţii, analizăm, judecăm, dezbatem, iar după o vreme poate reuşim să luăm decizii mai bune. Importante sunt criteriile pe baza cărora decidem (în anii ’80 criteriile au fost de performanţă pentru olimpiade şi rigurozitate teoretică, iar acestea nu au fost clar şi oficial abandonate nici în ziua de azi; prima categorie s-a transformat doar cu numele, în excelenţă, pe când a doua a suferit o serie de amputări, actualmente ajungându-se într-o ciudată degringoladă). Dar să revenim la articolul nostru:
Suma pătratelor catetelor este egală cu pătratul ipotenuzei. Așa sună una dintre cele mai cunoscute teoreme din geometria euclidiană, pe care mulți am învățat-o ca pe o poezie în gimnaziu: a² + b² = c².
Trebuie să apreciez în această intervenţie textul teoremei, adică enunţarea relaţiei fără folosirea cuvântului “lungimea”. Despre acest aspect am scris pendelete în postarea din 22 februarie 2019, de la adresa http://pentagonia.ro/teorema-lui-pitagora-si-ciocolata-ritter-sport-in-clasa-a-6-a/ (cu atenţionarea că de fapt sunt trei articole în cascadă). Eseul respectiv conţine inclusiv elemente evocate mai jos. Să continuăm cu articolul CEAE:
Teorema lui Pitagora a primit de-a lungul timpului numeroase demonstrații, dintre care unele geometrice, foarte frumoase. Acestea au nu doar avantajul de a le oferi copiilor o imagine care li se imprimă ușor în minte, cât mai ales de a putea fi făcute chiar de ei pe baza cunoștințelor elementare pe care le dețin deja. Astfel, copiii nu sunt nevoiți să memoreze formula fără să o înțeleagă, iar în eventualitatea în care o uită au la îndemână o cale rapidă pentru a o determina din nou.
Autorul articolului precizează clar (numai să avem “ochi să vedem şi urechi să auzim”): el ne vorbeşte despre numeroase demonstrații, dintre care unele geometrice (aha, deci există demonstraţii geometrice şi demonstraţii algebrice!), acestea foarte frumoase (adică atractive pentru sufletul şi mintea elevului). Acestea au nu doar avantajul de a le oferi copiilor o imagine care li se imprimă ușor în minte (aici, afirmaţia aproape se atinge cu cele spuse de Profesorul Hollinger în prefaţa ultimei sale culegeri), cât mai ales de a putea fi făcute chiar de ei pe baza cunoștințelor elementare pe care le dețin deja. Astfel, copiii nu sunt nevoiți să memoreze formula fără să o înțeleagă,(…)
Da, socrul meu avea prin anii ’90 un elev care ştia să turuie textul teoremei lui Pitagora cu o viteză de invidiat, dar habar nu avea despre cum să o folosească în calculele din probleme: “Măi, păi ştii sau nu teorema lui Pitagora?”. “Ba da!” răspundea acesta şi începea să o turuie de la capăt. În primul aliniat chiar este folosită expresia “mulți am învățat-o ca pe o poezie în gimnaziu”. În acest sens trebuie să precizez că eu nu le cer elevilor să ştie pe de rost textul teoremei. Revenim la citatele articolului CEAE:
Există pe YouTube o serie de animații și de experimente filmate, în care copiii pot vedea imediat cum suma ariilor pătratelor care au ca laturi catetele a și b este egală cu aria pătratului care are ca latură ipotenuza c. Acest lucru poate fi făcut, de exemplu, împărțind pătratele în pătrate mai mici, colorate, egale ca dimensiune. Copiii le pot număra și pot constata ei înșiși relația de egalitate.
Apreciez şi savurez din plin faptul că autorul/autorii articolului au trecut textul teoremei din zona numerică (pătratul lungimii ipotenuzei) în zona fenomenologică a ariilor (aria pătratului ipotenuzei), mult mai “vizibilă” pentru ochiul ne-experimentat al elevului mediu. Trec astfel peste faptul că au încărcat textul cu alte cuvinte (“aria pătratului care are ca latură ipotenuza c” în loc de “aria pătratului pe ipotenuza c, sau chiar “aria pătratului ipotenuzei c), punând acest gest pe faptul că au vrut să accentueze clar la adresa cititorilor mutarea de accent. Elevilor putem să le dăm desigur o variantă cât mai simplă, cât mai scurtă deci, pentru că oricum vor fi mulţi înclinaţi (sau puşi de către părinţi) să înveţe textul pe de rost. Şi dacă ei învaţă textul ca o poezie, noi trebuie să venim în întâmpinarea lor, astfel încât mintea lor să poată face cât mai uşor conexiunea cu cele văzute. În acest sens, cuvintele ne-esenţiale trebuie reduse la maximum. Să revenim la articolul analizat, unde găsim un magistral exemplu de predare prin problematizare:
Într-un experiment de pe YouTube, vedem o dovadă experimentală că Teorema lui Pitagora este adevărată. Ea este făcută cu ajutorul apei și ea poate reprezenta un bun punct de plecare al unei lecții despre Teorema lui Pitagora, pe care profesorul o poate începe cu o întrebare. De ce credeți că se întâmplă asta? Ceea ce văd elevii că se petrece în experiment îi nedumerește/ contrariază și îi face curioși să afle de ce se întâmplă așa lucrurile. Mai mult, își vor reaminti cu plăcere experimentul și peste 10-20 de ani. (aici este ataşat filmuleţul de pe youtube, de la următoarea adresă https://www.youtube.com/watch?v=CAkMUdeB06o )
Să lămurim deci această sugestie: dacă împărţirea pătratelor construite pe laturile triunghiului în pătrăţele egale (de pildă cum am făcut eu cu pătrăţele de ciocolată) ne sugerează egalitatea din teorema lui Pitagora pentru lungimi întregi, varianta din filmuleţul cu apă ce echivalează pătratul ipotenuzei cu pătratele catetelor se eliberează de spectrul lungimilor numere întregi (adică a tripletelor pitagorice) şi deschide poarta pentru un pas intuitiv spre orice lungimi la laturile triunghiului dreptunghic. Chiar dacă nu-şi dau seama pe loc de acest pas, se prea poate ca unii din elevi să realizeze ulterior ce s-a întâmplat. Aici ariile nu mai sunt împărţite în pătrăţele, ca un fel de unităţi de măsură, ci “curg” în mod continuu între cele două situaţii echivalente (apa din pătratele catetelor curge efectiv în pătratul ipotenuzei). Situaţia rămâne însă în spectrul vizualizării simple, fără a avea pretenţia unei demonstraţii adevărate.
Pe vremuri am avut tentativa de a construi pe o planşă pătratele din exteriorul unui triunghi dreptunghic, mărginite cu o bordură de carton mai gros, de cca. 1-2 mm. Apoi puneam cât mai dens un strat de boabe de orez în interiorul pătratelor catetelor. În final luam toată această cantitate de orez şi o rearanjam în pătratul ipotenuzei, justificând astfel în mod vizual practic afirmaţia din teorema lui Pitagora (merge şi altfel: umplem toate pătratele, iar apoi comparăm cantităţile, fie numărând boabele, fie cântărindu-le). Boabele mele de orez reprezentau astfel o trecere de la pătrăţelele în care sunt descompuse cele trei mari pătrate (reprezentând numerele întregi), către forma lichidă (reprezentând chiar şi mărimile iraţionale). Nu pot să susţin că am fost foarte entuziasmat de experimentul respectiv (consumă foarte mult timp), dar acum acesta capătă o relevanţă interesantă. Să revenim însă la articolul CEAE:
Urmează pasul 2 – demonstrarea Teoremei lui Pitagora. Un exemplu interesant de demonstrație este cel găsit într-un manual german de matematică de clasa a IX-a, publicat de Ernst Klett Verlag și utilizat în landul Baden-Württemberg.
Dacă aţi ratat momentul vă atenţionez eu acum: demonstraţia respectivă apare într-un manual pentru clasa a 9-a. Aha! Numai puţin, să ne lămurim: Ei numără clasele începând de la prima (noi avem mai întâi clasa pregătitoare), adică de la intrarea la şcoală după împlinirea vârstei de 6 ani, cum ar fi şi normal. Aşadar, clasa lor a 9-a corespunde ca vârstă clasei noastre a 8-a, cu deosebirea că ei nu au după acest an examen. Astfel, înţelegem că diferenţa este de doar un an, adică noi facem teorema lui Pitagora doar cu un an mai repede (dacă nu luăm în considerare experimentul ciudat din finalul clasei a 6-a). Dar oare, acest manual nu reia doar teorema lui Pitagora? Ei mai fac uneori recapitulări din anii precedenţi.
Mai există însă un aspect de care ar trebui să ţinem cont: după încheierea ciclului primar, ei au două tipuri de şcoli: Gymnasium (şcoli pentru elevii mai buni, din care se vor selecta cei care vor merge şi la facultăţi, cuprinzând clasele 5-12) şi Realschule (şcoli pentru elevii mai puţin înclinaţi spre învăţătură, din care se va forma viitoarea “clasă muncitoare”, încep tot în a 5-a, dar nu ştiu clar când se termină; este interesant că la ei cuvântul real reprezintă faptul că şcoala este mai apropiată de realitatea vieţii cotidiene, pentru elevii mai practici, dar neînclinaţi spre învăţarea teoretică; la noi cuvântul real înseamnă cu totul altceva).
Ca o paranteză la discuţia noastră, selecţia pentru cele două “filiere” se face la finalul clasei a 4-a, exclusiv pe baza caracterizărilor făcute de către învăţători, caracterizări deosebit de obiective, profesionist organizate pe itemi clari, cuprinzând o analiză detaliată şi verificabilă a multor aspecte din evoluţia şi din capacităţile dovedite de fiecare elev în parte. Familiile elevilor nu au nici cel mai mic cuvânt de spus în această selecţie: copilul este repartizat în urma studiului obiectiv şi gata.
Pe baza informaţiilor oferite, noi nu ştim în acest moment pentru care tip de şcoală este manualul din care sunt preluate imaginile din articolul CEAE. La o analiză serioasă a subiectului, aceste aspecte ar putea avea o oarecare relevanţă. Poate că în manualele pentru Gymnasium teorema lui Pitagora se face în clasa lor a 8-a, pe când la Realschule de abia în a 9-a. Este clar că o comisie care ar face o astfel de analiză cum vorbeam mai sus, ar trebui să ia în calcul toate aceste aspecte.
Pe de altă parte, de vreme ce discuţia alegerii unei demonstraţii la teorema lui Pitagora ne interesează oricum pentru clasa a 7-a, aspectul filierei manualului din Germania îşi pierde importanţa: în clasa a 7-a noi încă nu am selectaţi elevii, aşa încât trebuie să venim cu o demonstraţie cât mai accesibilă majorităţii (elevului mediu, cum spunea Hollinger). Dar, să revenim la articolul CEAE:
Se construiește un pătrat cu latura de lungime a + b și se desenează apoi patru triunghiuri dreptunghice, cu catetele a și b ca în figura din mijloc. Plecând de la această imagine, copii sunt puși să se gândească cum ar putea demonstra Teorema lui Pitagora mutând poziția triunghiurilor; desigur, nu li se arată imaginea din dreapta când li se cere acest lucru.
Mai întâi, ei observa că spațiul alb care rămâne în figura din mijloc este reprezentat de un patrulater cu laturile egale, de lungime c. Arătăm că este vorba despre un pătrat, demonstrând că are un unghi de 90 de grade – este vorba despre unghiul δ. Astfel, scădem din unghiul de 180 de grade suma unghiurilor α și β, despre care știm (pe baza proprietăților triunghiului dreptunghic) că este de 90 de grade. Se pot face demonstrații similare și pentru celelalte 3 unghiuri ale patrulaterului cu latura c. Prin urmare, acesta este un pătrat, iar suprafața sa este c².
Ulterior, elevii trebuie să se gândească cum ar putea să mute triunghiurile a.î. să rezulte două pătrate de laturi a și b. După ce se translatează trei din cele patru triunghiuri dreptunghice, ele vor ajunge în pozițiile pe care le vedem în cea de-a treia figură. Vom obține astfel două pătrate mai mici, având ca laturi cateta a, respectiv b. Suprafața totală a spațiului alb rămâne aceeași ca în figura din mijloc. De această dată nu vom mai avea însă un singur pătrat, ci două, cu suprafețe mai mici. Există și alte moduri de translatare a triunghiurilor a.î. să se obțină cele două pătrate de laturi a și b.
Așadar suma suprafețelor celor două pătrate, a² + b², este egală cu suprafața pătratului mare, c². Chiar dacă unii elevi nu vor reuși să găsească singuri soluția, ei o vor înțelege când le va fi prezentată de profesor.
Intervin aici întrerupând articolul CEAE cu o scurtă idee practică: cred că îmi voi construi din carton o astfel de machetă pe care elevii să poată translata cu adevărat triunghiurile; mai exact, cred că voi face mai multe seturi, astfel încât să-i pun să lucreze pe grupe.
În altă ordine de idei – pentru cei care-mi lecturează constant articolele – mai ţineţi minte afirmaţia d-ne Birte Vestergaard? Elevii buni la matematică vor avea bucuria că “eu am descoperit asta!”, pe când cei slabi se vor bucura că “eu am înţeles asta!”. Elevilor buni trebuie să le oferim ocazia să descopere demonstraţia (iar pentru asta trebuie să-i pui să cerceteze, adică să predai prin problematizare; iar dacă o faci pe grupe, mai mulţi elevi vor avea ocazia de a se implica, de a descoperi chiar ei), iar în final elevilor mai slabi trebuie să le-o explicăm, oferindu-le şi lor ocazia să înţeleagă demonstraţia (Chiar dacă unii elevi nu vor reuși să găsească singuri soluția, ei o vor înțelege când le va fi prezentată de profesor).
Uau! Vedeţi? Nu trebuie neapărat să preluăm idei doar din “străinezia”; şi la noi sunt oameni care spun lucruri de valoare; trebuie doar să avem aplecarea să-i ascultăm cu atenţie. Dar dacă auzim aceleaşi lucruri spuse şi de unii şi de alţii, atunci este cu atât mai convingător. Să revenim la studiul nostru:
În Germania, lecția despre Teorema lui Pitagora este predată conform paradigmei constructiviste. Pentru a o demonstra, elevii pleacă de la ceea ce știau de dinainte – cum se determină aria pătratului. Astfel, ei nu vor trebui să memoreze că a² + b² = c², fără să o înțeleagă (cum se întâmplă în cazul unora dintre ei – dintre elevii noştrii). Dacă vor uita formula peste ani de zile, vor putea să ajungă într-un mod logic și intuitiv la ea.
Da! Da! Da! De curând m-am uitat într-un “manual auxiliar” pentru clasa a 6-a (deci nu într-un manual oficial). Ideea de a demonstra (aşadar primele demonstraţii), de a justifica măcar superficial un rezultat cuprins ca teoremă (mediana pe ipotenuză, cateta opusă unghiului de 30o, sau reciprocele), această idee lipseşte cu desăvârşire acolo (unele nu au nici măcar figură alăturată pentru a susţine înţelegerea elevilor). Acea “lecţie” despre triunghiul dreptunghic (din finalul clasei, deci care ar fi putut conţine anumite justificări în loc de demonstraţii), aceasta este doar o colecţie de texte de învăţat pe de rost, fără orice urmă de înţelegere pentru elevi. Lecţia respectivă se încheie cu teorema lui Pitagora, ce le este dată elevilor exact cum este spus mai sus: în orice triunghi dreptunghic, avem a² + b² = c²! Atât, nimic mai mult!
“Care-i problema?”, veţi spune, fiind vorba despre un auxiliar. Când însă manualul folosit de clasa respectivă este şi mai slab, existând recomandarea explicită a profesoarei de la clasă de a nu-l folosi (dar, am verificat şi eu pe concret, şi chiar e de toată jena!), atunci auxiliarul capătă o importanţă mult mai mare şi ar trebui să acţioneze ca “o plasă de siguranţă” pentru formarea gândirii elevului (mai ales că profesoara respectivă obişnuieşte a-i pune pe elevi să copieze lecţia din carte!).
Simt aici un fenomen ciudat: pe de-o parte, ca autori de manuale, unii colegi se simt obligaţi să dea demonstraţii cât mai elevate, cât mai sofisticate, în ultimă instanţă cât mai grele, accesibile câtor mai puţini elevi; pe de altă parte considerăm demonstraţiile total nerelevante (pentru lecţia de zi-cu-zi, de pildă în pregătirea evaluărilor, a examenelor etc.), aşa încât, dacă avem libertatea, cum ar fi în cazul redactării unor auxiliare, atunci eliminăm cu totul ideea de a demonstra un rezultat important (“trebuie să-i înveţe textul, că doar am scris că-i teoremă”). Oare, o variantă de mijloc nu ar fi mai sănătoasă? Să revenim la articol. Aşadar:
Cum este abordată Teorema lui Pitagora în România?
Imaginea folosită în manualul de matematică, de clasa a VII-a, publicat de Intuitext, are legătură cu viața reală – o scară sprijinită de o casă, pe care niște copii trebuie să se urce pentru a ajunge la un cuib de păsări. Elevii sunt puși să afle lungimea scării (ipotenuza unui triunghi dreptunghic) știind cele 2 catete. Acest mod de a introduce Teorema lui Pitagora nu generează însă un conflict cognitiv în mintea elevului. Sara reușește să calculeze rapid lungimea scării, folosind formula făcută în clasa a VI-a (c² = a² + b²). În acest manual, se face și demonstrația teoremei – pentru aceasta se pornește de la teorema catetei pe care copiii trebuie să și-o amintească din clasa a VI-a: într-un triunghi dreptunghic lungimea unei catete este media geometrică dintre lungimea proiecției sale pe ipotenuză și lungimea ipotenuzei. Acest mod de a face demonstrația nu este unul intuitiv pentru copii și se bazează din nou pe aplicarea unei formule memorate (adică avem de-a face tot cu calcul algebric).
Acest aliniat – analiza situaţiei din manualul Intuitext – are mai multe aspecte ce merită analizate. Ideea de a porni de la o situaţie practică este deosebit de bună, dându-i elevului o oarecare justificare a utilităţii elementelor de învăţat. Aparent şi aceasta este o altfel de situaţie, doar că nimeni nu va calcula ce lungime trebuie să aibă scara, cu un rezultat de 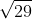 m. În situaţia respectivă, cu înălţimea până la streaşină de 5 m, era evident că este nevoie de o scară mai lungă de atât. Şi cât mai lungă? Păi, nu-ţi face nimeni o scară pe măsura nevoilor de moment. Cum arată şi desenul, probabil că este nevoie de o scară de 6 m (care trece puţin de straşină). Aşadar, punerea problemei se vrea practică, dar se vede că autorii nu prea au experienţă despre ce înseamnă practică pentru omul de rând.
m. În situaţia respectivă, cu înălţimea până la streaşină de 5 m, era evident că este nevoie de o scară mai lungă de atât. Şi cât mai lungă? Păi, nu-ţi face nimeni o scară pe măsura nevoilor de moment. Cum arată şi desenul, probabil că este nevoie de o scară de 6 m (care trece puţin de straşină). Aşadar, punerea problemei se vrea practică, dar se vede că autorii nu prea au experienţă despre ce înseamnă practică pentru omul de rând.
Însă, oricum, Sara – deşteapta clasei – nu se împiedică de astfel de aspecte. Eu mă întreb, oare câte eleve cu numele de Sara au fost luate la mişto de către colegi în urma acestei situaţii în diverse clase din ţară? Oare, nu-i dă nimeni în judecată pe aceşti autori, sau pe alţii pentru posibila generare de situaţii favorizante de bullying? N-am nimic cu folosirea numelor, dar Sara asta “se cam dă deşteaptă” în faţa colegilor săi. Imaginaţi-vă diverse scenarii posibile într-o clasă, în care o oarecare Sara mai bună la învăţătură este catalogată drept tocilară.
În altă ordine de idei, aliniatul respectiv cred că are şi o greşeală din partea autorilor de la CEAE, anume afirmaţia că la demonstrare se pornește de la teorema catetei pe care copiii trebuie să și-o amintească din clasa a VI-a. Nu trebuie să şi-o amintească din clasa a 6-a, pentru că nu se face atunci. Trebuie să şi-o amintească doar din lecţia precedentă. Greşeala este totuşi insignifiantă la nivelul întregului articol.
Toate acestea sunt însă detalii; un aspect mai important ce ar trebui discutat este afirmaţia ce am îngroşat-o, anume că Acest mod de a introduce Teorema lui Pitagora nu generează însă un conflict cognitiv în mintea elevului. Oare ce a vrut să spună autorul articolului de la CEAE? În altă ordine de idei, despre abordarea intuitivă a materiei am vorbit cu diferite alte ocazii. Punctez doar faptul că şi aici este amintită: Acest mod de a face demonstrația nu este unul intuitiv pentru copii și se bazează din nou pe aplicarea unei formule memorate.
Finalul aliniatului respectiv – adică avem de-a face tot cu calcul algebric – aduce însă, chiar şi în paranteză, un aspect total neglijat în România ultimilor 40 de ani, anume că la noi matematica este trasă tot mai mult în zona algebrică a gândirii, în detrimentul gândirii geometrice (gândirea numerică, algoritmică faţă de gândirea spaţială, pe bază de forme). Ce vrea să spună această afirmaţie? “Doar, aici facem geometrie!”, veţi spune.
Nu-i chiar aşa de simplu. Acesta este un subiect mult prea vast pentru a-l aborda acum, dar pot să dau aici un indiciu: în lucrarea americană evocată în prima parte a analizei, demonstraţia despre care ne-a vorbit d-na Marisha Plotnik este demonstraţia cu numărul 82 din capitolul cu demonstraţii algebrice! Da, demonstraţia respectivă este privită ca demonstraţie algebrică. După ce “digeraţi” acest fapt, puteţi să recitiţi întregul articol CEAE. Păi, dacă acea demonstraţie a fost considerată “algebrică”, atunci demonstraţia folosind factorul comun şi teorema catetei (cea uzuală la noi), cu atât mai mult este una algebrică.
Chiar şi în aliniatul următor este reluată ideea, fapt ce dovedeşte cumva înclinaţia noastră spre algebrizarea oricărei demonstraţii. La noi, o demonstraţie este cu adevărat de băgat în seamă doar dacă este redactată într-un limbaj cât mai algebric. La noi doar limbajul algebric este considerat cel adevărat matematic. Dar să continuăm cu articolul CEAE:
În manualul de la Editura Litera, sunt folosite figuri asemănătoare cu cele din manualul german, prezentate mai sus, copiilor le este lăsat puțin spațiu pentru a raționa individual. Mai mult, raționamentul este complicat și se merge tot pe calcul algebric. Pașii raționamentului sunt făcuți acum în sens invers, începând cu triunghiurile deja translatate (a se vedea imaginea din dreapta din manualul german). Dacă elevii urmăresc calculul din filmulețul de la pagina 201 a manualului, există riscul pentru o bună parte dintre ei să piardă cu ușurință firul explicației.
Time out! Trebuie să intervin din nou. Părerea mea este că autorul articolului CEAE a fost deosebit de politicos, abordând un ton extrem de conciliant. Uitaţi-vă, vă rog, din nou la demonstraţia din manualul acestei edituri şi analizaţi-vă gândurile, anume ce efort trebuie să faceţi ca să înţelegeţi mersul lucrurilor. Uitaţi-vă apoi la imaginile demonstraţiei prezentată din “manualul nemţesc”. Apoi, după ce aţi citit cu atenţie, vă las pe dvs., onoraţii cititori, să judecaţi. De ce trebuie transformată într-o formă atât de complicată, cu calcule algebrice, o demonstraţie geometrică vizuală (pur geometrică!!!), care este deosebit de intuitivă? De ce?
Ce ne facem cu acest impuls năucitor din mintea unor colegi, de a complica lucrurile atât de mult, cât mai mult dacă se poate? Asta înseamnă a face matematică? În momente ca acesta apare absolut natural impresia că “se doreşte” a se complica lecţiile cât mai mult, doar-doar vor fi cât de puţin elevi care să înţeleagă matematica (oculta pseudo-ştiinţifică mioritică?). Eu personal recunosc aici: nici nu am avut răbdare la început să analizez demonstraţia respectivă în cele mai mici detalii. Păi atunci, cum ar avea răbdare un elev să o facă? Elevul ar trebui să o poată înţelege de unul singur, că de aia este făcut manualul, nu ca să vină în paralel cineva acasă şi să-i explice ce scrie acolo.
Acest aliniat mai are un pasaj important: copiilor le este lăsat puțin spațiu pentru a raționa individual. Acest aspect este de o fineţe deosebită din punct de vedere metodico-didactic. Noi trebuie astfel să predăm încât mintea elevului să “aibă loc să mişte” relativ liber. Doar aşa elevul se va obişnui încet, tot mai mult să gândească. Doar atunci elevul va avea sentimentul că gândurile respective sunt şi “ale sale”. Dacă nu-i lăsăm defel “spaţiu de mişcare”, ci îl obligăm să înveţe o demonstraţie mot-a-mot (cuvânt cu cuvânt), atunci elevul va resimţi gândurile respective ca străine şi automat va fi înclinat să le refuze. Sau dimpotrivă, un alt elev poate se va obişnui doar să înveţe pe de rost o teorie, nedezvoltând însă abilităţi de proprie judecată şi gândire (cu ambele alternative ne întâlnim des, deşi este clar că acestea nu duc la situaţii dezirabile). Dar, să terminăm “de lecturat” articolul de pe blogul CEAE:
Remarcăm în ultima vreme efortul mai multor autori de manuale de matematică din România de a pleca de la situații din viața reală sau de a se raporta la acestea, însă adeseori demersurile au loc la un nivel formal. Acest lucru se întâmplă pentru că nu s-au făcut suficienți pași pentru a schimba semnificativ paradigma utilizată în predarea matematicii în gimnaziu (în loc să devină inductive, cum se întâmplă în tot mai multe țări europene, abordările la noi sunt încă preponderent deductive și calculul algebric are în continuare o pondere importantă). Prin urmare, pentru un procent semnificativ dintre elevi, matematica înseamnă memorarea și reproducerea formulelor de calcul și aplicarea algoritmilor de rezolvare de probleme. Or, matematica ar putea să contribuie mai mult în a le dezvolta copiilor o gândire structurată și logică.
Pentru cine a ratat momentul de la început, precizez din nou cum trebuie citite afirmaţiile din paranteză: paradigma utilizată în predarea matematicii în gimnaziu ar trebui să devină una inductivă, nu pentru că aşa se întâmplă în tot mai multe țări europene, ci pentru că aşa este potrivit psihologiei vârstelor gimnaziale (pentru o întreagă populaţie şcolară, până la 14-15 ani), dar şi mai târziu. Legat de afirmaţiile din ultimele două fraze nici nu mă gândesc să le analizez acum. Acestea sunt atât de valoroase încât merită fiecare câte un eseu separat de discuţii şi analize.
Dar, cine trebuia să facă paşii pentru schimbarea paradigmei utilizate în predarea matematicii gimnaziale? Profesorii, fiecare pentru el? Nu prea cred. Nişte oameni care în ultimele câteva zeci de ani au trăit doar într-o paradigmă şi într-o stare generală de executanţi ai politicilor educaţionale venite “de sus”, aceştia sigur nu vor fi în stare să contribuie în mod sănătos la o schimbare de paradigmă ca cea evocată în ultimul aliniat. Scurtele indicaţii (foarte valoroase de altfel) din programa 2017 nu au forţa de a duce la o schimbare de paradigmă.
Merită să scot în evidenţă aici un aspect relativ nou: geometria sintetică a fost scoasă din licee prin 1997 (orientativ). Ca urmare, avem deja prin şcoli colegi profesori care au cam încheiat-o cu geometria după clasa a 8-a. Aceştia nu au mai apucat să reia şi să aprofundeze geometria (atât cea plană, cât şi cea în spaţiu) la un nivel mai matur. Iar în facultate sigur nu au mai reluat aceste aspecte. Aceşti colegi mai tineri cunosc doar forma deductivă şi algebrizată până în “măduva oaselor”. Cum să-şi schimbe aceştia predarea? În general, cea mai mare parte a profesorilor sub 45-50 de anu nu au prins predarea inductivă nici ca elevi. Pe baza a ce să poată ei acum face o schimbare de paradigmă?
Eu mă lupt de 25 de ani să înţeleg aceste lucruri, să îmi modific propria paradigmă de predare şi văd cât este de greu (eu, cel care vreau să mă schimb, în luptă cu mine, cel ce vine cu apucăturile profesionale vechi). Pentru o adevărată conştientizare, părţi din acest ultim aliniat citat ar trebui să devină obligatoriu de lecturat zilnic, de către toţi profesorii. Totuşi, la fel ca autorii articolului din CEAE, nici eu nu-mi permit să dau sfaturi despre cine ar trebui să se ocupe de această modificare de paradigmă (pentru ca lucrurile să se şi întâmple cu adevărat şi în mod sănătos), dar sigur treaba asta nu poate fi lăsată pe seama profesorilor de la clasă.
*
Acesta a fost articolul apărut pe blogul CEAE, însoţit şi întrerupt de câteva “scurte” comentarii personale. Dacă în prima parte a analizei mi-am spus punctele de vedere mai mult stârnite de comentariile la reluarea articolului pe edupedu.ro, în această a doua parte a analizei mi-am exprimat punctele de vedere direct la afirmaţiile din articolul iniţial.
Da, acum chiar cred că mă opresc cu analiza (la cât de lungă a ieşit, chiar poate fi clasificată ca exagerare – cu totul sunt aproape 16 pagini A4 doar text, scris cu 12), dar vreau să aduc aici şi o mică propunere: demonstraţia din manualul nemţesc ar putea fi folosită clar pentru includerea teoremei lui Pitagora în capitolul despre arii din toamna clasei a 7-a, statutând astfel totodată şi folosirea acestei teoreme în calculele pentru determinarea segmentelor necesare la arii sau perimetre. În ultimii ani am putut observa cum foarte mulţi profesori se feresc încă a folosi teorema lui Pitagora în acest capitol, deşi la ora actuală este cunoscută de la sfârşitul clasei a 6-a, cel puţin ca aplicaţie încă nedemonstrată. Atunci, de ce mulţi profesori încep să o folosească în probleme de-abia în primăvară după ce teorema apare şi cu demonstraţie (după asemănarea triunghiurilor şi teorema catetei). Poate, dacă ar şi avea-o de demonstrat prin arii, colegii s-ar “aventura” să o şi folosească la clasă chiar din capitolul despre arii. Sau, poate, un “ordin de sus” în acest sens ar rezolva mai eficient situaţia. Fără teorema lui Pitagora, capitolul despre arii din toamna clasei a 7-a este sec, doar cu aplicaţii grele, potrivit elevilor mai buni, în continuare înjositor pentru elevii de rând.
Revenind la demonstraţia cu cele patru triunghiuri în interiorul unui pătrat, trebuie să mai precizez ceva: dacă undeva înaintea acesteia, într-o oră precedentă de aplicaţii la patrulatere, s-ar face problema care cere demonstrarea faptului că figura cuprinsă între cele patru triunghiuri este tot un pătrat (adică un romb – congruenţa triunghiurilor, dar cu cel puţin un unghi drept, deci pătrat), atunci demonstraţia respectivă la teorema lui Pitagora devine chiar una doar orală, având drept urmare un nivel de accesibilitate deosebit de bun la toţi elevii.
Schimbând puţin linia discuţiei, merită precizat că aici nu este vorba despre “care demonstraţie o facem pentru teorema lui Pitagora?”. În mod excepţional teorema lui Pitagora ar trebui eliberată de paradigma generală a “cursului euclidian” (fiecare teoremă cu demonstraţia ei, ca urmare deci la fiecare teoremă doar o singură demonstraţie), permiţând profesorilor să predea – iar elevilor să cunoască – diferite şi diverse demonstraţii. Cea evocată din manualul nemţesc ar merita să fie prima din clasa a 7-a, dar sunt multe altele ce pot veni în continuare ca aplicaţii la noile lecţii. În această categorie s-ar încadra şi demonstraţia pe baza teoremei catetei, dar şi multe altele.
Am rămas însă cu o datorie legată de comentariile la articolul de pe blogul CEAE: oare ce a vrut să transmită autorul în aliniatul în care comenta situaţia din manualul Intuitext, când a spus cu referire la felul în care decurge raţionamentul: Elevii sunt puși să afle lungimea scării (ipotenuza unui triunghi dreptunghic) știind cele 2 catete. Acest mod de a introduce Teorema lui Pitagora nu generează însă un conflict cognitiv în mintea elevului.
Ce conflict cognitiv trebuie generat? Este nevoie de un conflict cognitiv pentru a înţelege o demonstraţie? Este bine sau nu să apară un conflict gognitiv? Eu m-aş încumeta să încerc un răspuns (chiar îmi stă pe limbă), dar nu am nici cea mai mică garanţie că aşa este. Prefer de data asta să tac şi cel mult să relansez întrebarea, cel mai bine către autorul articolului: stimate coleg, ce aţi vrut să spuneţi aici? Pentru că, dacă este aşa cum simt eu, atunci acest gând ar deschide poarta spre o altă mare schimbare în predarea matematicii. Dacă nu vom primi în următoarea perioadă un răspuns, atunci poate totuşi mă voi încumeta eu să dau o explicaţie. Titus pitagoreanul (Grigorovici Constantin Titus)
P.S. În ambele părţi ale acestei analize m-am lovit în anumite momente de situaţii în care am impresia că profesori de matematică din ţara noastră doresc cu cea mai mare hotărâre să aducă în faţa elevilor o materie cât mai complicată, cât mai inaccesibilă. Dacă vă sună ca exagerată această afirmaţie, dacă o consideraţi drept o “acuză nefondată”, atunci vă mai dau un exemplu: gândiţi-vă cât de repede apar direct aplicaţii cu numere iraţionale la teorema lui Pitagora (după ce aceasta a fost în sfârşit predată, fie şi prin teorema catetei). În acel moment, adică la prima lecţie, la cei mai mulţi profesori apar rapid şi exemplele cu numere iraţionale, la unii chiar din prima (vedeţi exemplul cu Sara şi lungimea scării), dar oricum cel târziu de la a doua sau a treia aplicaţie. N-am prea întâlnit profesori care să stea în prima oră doar la nivelul tripletelor pitagoreice, adică în zona de comfort a tuturor elevilor, respectând astfel capacitatea uneori lentă de adaptare a elevului mediu la un algoritm nou. Elevul mediu ar avea nevoie de o oră la clasă, cu exemple cât mai multe, plus o tema corespunzătoare, pe care să o şi înţeleagă şi să o poată face singur, fără ajutor din partea altcuiva. La algoritmul nou din aplicarea teoremei lui Pitagora, elevul mediu are nevoie să rămână măcar o oră în zona sa de comfort numeric, ca să se poată concentra la aspectele noi ce ţin de calculul specific. Doar apoi acesta va putea face pasul fără spaime în zona iraţională.
Am atins aici un subiect ciudat: cei mai mulţi profesori nici nu prea cunosc tare multe triplete pitagoreice (triplete de numere naturale care să verifice relaţia teoremei lui Pitagora). Majoritatea cunosc aparent doar tripletul (3; 4; 5), cu primele amplificări şi eventual încă tripletul (5; 12; 13). În acest sens, eu folosesc toată plaja de triplete pitagoreice cu lungimi până la 100 (deşi am fost acuzat că astfel terorizez copiii; ar fi de discutat cum îi terorizăm mai tare pe elevi, cu radicali din pătrate perfecte de cel mult patru cifre sau dându-le din prima numere iraţionale, care sunt destul de neînţelese? Mă refer aici la faptul că majoritatea elevilor se blochează când sunt întrebaţi despre lungimea aproximativă a unor numere iraţionale de forma 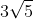 ; la numere de forma
; la numere de forma 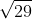 aproximarea este ceva mai accesibilă).
aproximarea este ceva mai accesibilă).



In Germania, la unele gimnazii se ține tot mai puțin cont de acele ,, caracterizări,, făcute de către învățători pentru inscrieea elevului la instituția respectivă. Contează in primul rând situația școlară a a elevului dovedită prin acte. Dacă ești elev bun/f. bun te inscri la orice Gimnasium. Caracterizarea e,, luată,, doar ca ceva informativ. Se,, plang,, unii directori de Gimnasium că din cauza acestor ,,caracterizări,, care nu sunt chiar atat de obiective pe cât s-ar vrea, s-au pierdut valori. In trecut, elevi cu situații deosebite la învățătură au fost respinși la unele gimnazii din cauza acestor,, caracterizări ,, dar au facut performanță la alte gimnazii unde au fost inscrisi si unde nu s-a tinut cont de aceste,, caractetizari,, Vă spun din proprie experiență că nu se prea ține cont de aceste caracterizări, ci de situatia la învățătură. Poate cu ani in urmă erau luate in calcul….acum sunt doar informative
Toate cele bune!
Săracu Pitagora, cred că se răsucește în mormânt, atâta vorbărie sterilă, înșiruire de cuvinte fără formă și fond. Am două licențe în construcții, se calculau structurile de rezistență cu riglă de calcul, construcții ce sunt și în ziua de azi, și voi faceți teoria chibritului. Vorbă multă sărăcia omului, de aceea nu se face nimic, vă pierdeți în teorii inutile. Dacă tot sunteți atât de pricepuți, nu ne spuneți ce calcule a folosit Anghel Saligni în proiectele lui? Sper că știți cine este și ce a construit, nu vă rezumati numai la podurile dunărene.
q.e.d.