De multe ori elevii sunt bulversaţi de denumirile date de matematicieni diverselor clase de numere: numerele naturale şi cele reale sunt ceva mai clare, pe când cele întregi şi cele raţionale nu coincid nici măcar la prima literă cu denumirea denumirea dată mulţimilor. Apariţia, din câte ştiu doar în România, a unei notaţii pentru mulţimea numerelor iraţionale, care nu respectă modelul de extindere al precedentelor mulţimi, îi bulversează şi mai mult pe elevi (nu avem, de pildă, o denumire pentru numerele raţionale care nu sunt întregi).
Fără pretenţia de a a fi găsit forma ideală de predare, vă prezint totuşi pozele tablei de la lecţia ce o fac de mulţi ani în această formă. Concret, lecţia le-o predau elevilor în patru forme succesive diferite, fiecare cu povestea ei (totul într-o oră, chiar mai puţin).
În prima formă le şi spun elevilor că îi invit la o călătorie cu un balon cu aer cald, în care vom survola de la mare înălţime matematica. Astfel, în timpul zborului vedem operaţia de bază (adunarea) cu operaţia de probă (scăderea). O adunare repetată înseamnă înmulţirea, care are ca operaţie de probă scăderea. O înmulţire repetată reprezintă operaţia de putere, având ca probă rădăcina (aici analogia este cam subţire, deoarece elevii nu cunosc decât rădăcina pătrată, da’ nu ne împiedicăm de astfel de detalii minore). Cele trei operaţii directe aplicate pe numere naturale dau întotdeauna rezultate naturale. Dimpotrivă, fiecare operaţie de probă, lăsată să opereze la întâmplare, generează un nou tip de numere.
Din câte ştiu, denumirile celor patru mulţimi au fost date de către David Hilbert, aşa că, cel puţin în cazul numerelor întregi şi a celor raţionale am căutat în limba germană. Astfel, litera Z a fost aleasă de la cuvântul Zahl (număr în germană, zählen = a număra) iar litera Q de la cuvântul Quozient (cât, adică rezultatul unei împărţiri, tot din germană). Nu sunt sigur, este doar o presupunere, dar această teorie le dă elevilor o explicaţie plauzibilă.
A doua formă oferită scoate în evidenţă exact ce am prezentat în prima parte, anume că fiecare operaţie de probă nouă duce la o extindere a mulţimii de numere. Imaginea este una de pungă în plasă în sacoşă în geamantan (putem spune şi pungă în sertar în dulap în cameră). Pentru stabilitatea înţelegerii am păstrat şi culorile folosite iniţial.
A treia formă este probabil cea mai cunoscută; singura observaţie ar fi că la trecerea de la mulţimea Z la Q le atrag atenţia elevilor că nu mai putem prezenta numerele într-o secvenţă ordonată fără lipsuri.
Ultima formă, cea a axei numerelor, se înţelege cel mai greu din această imagine. Pe tablă, eu am păstrat diferitele culori iniţiale şi am desenat numerele: la început cele naturale ca paşi, la fel apoi şi cele întregi, apoi cel raţionale cu multe liniuţe (cele care dau impresia de iarbă), iar în final am evidenţiat faptul că numerele reale umplu toată axa, trăgând în sfârşit concret axa numerelor. Deci, să fie clar: axa numerelor nu am desenat-o de la început, ci numerele le-am poziţionat iniţial doar aliniate.
Titus Grigorovici



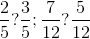 .
.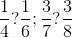 .
.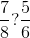 , acestea se pot reprezenta fiecare ca parte dintr-un întreg circular; din compararea celor două desene alăturate se poate stabili care fracţie este mai mare.
, acestea se pot reprezenta fiecare ca parte dintr-un întreg circular; din compararea celor două desene alăturate se poate stabili care fracţie este mai mare. şi
şi  se pot compara reprezentându-le grafic prin împărţirea unui dreptunghi cu lăţimea de 5 şi lungimea de 7 pătrăţele. Pentru prima fracţie împărţim cu o culoare întregul pe lăţime în cinci fâşii din care haşurăm cu această culoare trei fâşii, iar pentru a doua fracţie împărţim întregul pe lungime cu o altă culoare în şapte fâşii din care haşurăm cu această a doua culoare doar patru fâşii. În final avem dreptunghiul întreg împărţit de fapt în 35 de pătăţele, prin cele două culori, şi trebuie doar să numărăm câte sunt mai multe, cele din prima sau cele din a doua culoare. Este clar că această metodă deschide uşa pentru aducerea la numitor comun, dar este recomandabil să lăsăm mai spre final metodele foarte generale (cunoscând o metodă generală, elevul va accepta mai greu alte metode; în acest caz nu ne putem atinge unul dintre obiectivele majore ale unui învăţământ sănătos: deschiderea cât mai largă a minţii elevului).
se pot compara reprezentându-le grafic prin împărţirea unui dreptunghi cu lăţimea de 5 şi lungimea de 7 pătrăţele. Pentru prima fracţie împărţim cu o culoare întregul pe lăţime în cinci fâşii din care haşurăm cu această culoare trei fâşii, iar pentru a doua fracţie împărţim întregul pe lungime cu o altă culoare în şapte fâşii din care haşurăm cu această a doua culoare doar patru fâşii. În final avem dreptunghiul întreg împărţit de fapt în 35 de pătăţele, prin cele două culori, şi trebuie doar să numărăm câte sunt mai multe, cele din prima sau cele din a doua culoare. Este clar că această metodă deschide uşa pentru aducerea la numitor comun, dar este recomandabil să lăsăm mai spre final metodele foarte generale (cunoscând o metodă generală, elevul va accepta mai greu alte metode; în acest caz nu ne putem atinge unul dintre obiectivele majore ale unui învăţământ sănătos: deschiderea cât mai largă a minţii elevului).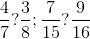 .
. şi
şi  , comparându-le (eventual grafic) cu fracţia intermediară
, comparându-le (eventual grafic) cu fracţia intermediară  , care este destul de cunoscută şi vizual. Deci
, care este destul de cunoscută şi vizual. Deci 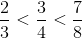 . Un exemplu în acest sens ar fi şi următorul: fracţiile
. Un exemplu în acest sens ar fi şi următorul: fracţiile  şi
şi 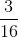 pot fi comparate cu
pot fi comparate cu  .
.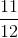 şi
şi 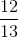 , diferenţele până la un întreg sunt
, diferenţele până la un întreg sunt 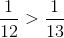 . Este evident că
. Este evident că 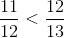 .
. .
.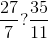 .
.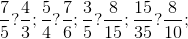
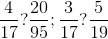 .
.