Afirmaţiile din emisiunea TVR1 prezentate în postarea precedentă – că meditaţiile paralele cu şcoala reprezintă un adevărat sistem de dopaj – au fost rezumate pe edupedu.ro în postarea lui Ştefan Lefter din 9 aprilie la adresa https://www.edupedu.ro/profesorul-radu-gramatovici-un-copil-mediu-nu-o-sa-scape-fara-meditatii-la-matematica-pentru-ca-asa-cum-e-facut-sistemul-ca-sa-beneficieze-de-scoli-bune-va-trebui-sa-intre-in-acest-sistem-de-dopaj/ În această postare autorul atrage atenţia şi asupra uneia mai vechi, din 14 martie 2024 (chiar de ziua lui pi), https://www.edupedu.ro/florian-lixandru-secretar-de-stat-meditatiile-sunt-in-mare-parte-o-moda-dar-si-o-necesitate-in-anumite-situatii-nu-mi-se-pare-deontologic-ca-un-cadru-didactic-sa-lucreze-in-particular-cu-elevii-d/ , generând astfel un fel de “dialog” între cei doi domni. A doua zi Vlad Petreanu, Luca Pastia, George Zafiu au dezbătut şi ei situaţia în Deşteptarea la Europa FM (de găsit în Podcast-ul din 10 aprilie între minutele 4 şi 22). Prezint în continuare o selecţie a discuţiilor din acea dimineaţă, ascultată iniţial în maşină în drum spre şcoală.
VP: Cred că în ţara asta toţi copiii fac meditaţii, care ajung la facultate (…) Fostul decan al Facultăţii de Matematică Profesorul Radu Gramatovici (…) a lansat recent o critică foarte dură la modul în care este organizat învăţământul românesc. Un profesor important din ţara asta spune că învăţământul este de fapt un sistem de dopaj! Adică, fără meditaţii, care reprezintă sistemul de dopaj, nu poţi să progresezi.
LP: Ok, dânsul a dus-o în extremă, adică ce descrie acolo, cu astea “să te trezeşti noaptea din somn” e valabil pentru copiii care vizează Sava, Lazăr, liceele unde se intră cu peste 9,90, sau în cazul elevilor de liceu facultăţi de top.
VP: Domnii de la minister consideră că meditaţiile sunt aşa, pentru elevii care – frate! – deja se plictisesc la şcoală şi atunci vor să facă ceva în plus. Aşa crede Domnul Florian Lixandru. (…) Iată două opinii complet diferite până la urmă. Prima: în actualul sistem meditaţiile sunt dopaj şi un elev mediu nu poate merge mai departe fără meditaţii, asta spune Domnul Gramatovici. Domnul Lixandru de la Minister, Secretarul de Stat spune: de fapt meditaţiile sunt doar pentru elevii care vor să facă performanţă; e vina părinţilor că întreţin modelul, că în rest poţi să faci lucruri foarte bune şi fără meditaţii.
VP:Întrebare şi pentru voi, prieteni care ne ascultaţi: credeţi că meditaţiile sunt dopaj şi n-ai încotro dacă vrei ca odrasla să aibă o minimă şansă în viaţă? Sau meditaţiile sunt doar pentru cei care vor să fie campioni? La ce servesc meditaţiile în România? Dacă sunt inevitabile? Dacă sunt o modă? Dacă sunt o fiţă? Se poate intra la liceu/ facultate fără meditaţii? Dacă eşti un copil mediu (…) Paradoxal, se pare că e mai uşor să intri la facultate decât la liceu, acum, mi se pare că la liceu este o concurenţă înspăimântătoare.
GZ: Cea mai mare bătaie e pe liceu, (…)
LP: Momentul determinant în formarea unui om în momentul de fată în România este examenul din clasa 8-a, Evaluarea Naţională, care după aia îţi dă un liceu, de und poţi să decolezi sau unde poţi să te prăbuşeşti.
VP: (…) Se mai poate fără meditaţii în România? La ce sunt bune ele şi ce se întâmplă dacă nu faci meditaţii? După o pauză de publicitate, domnii din Deşteptarea revin “dând microfonul” ascultătorilor:
Mihaela, Bucureşti: fiica mea – acum are 27 de ani – nu a făcut o oră de meditaţii în toată viaţa ei. Ba da, a făcut la engleză în primii ani, 7 ani, 8 ani, 9 ani. Apoi a învăţat ea, că i-a plăcut să fie prima în clasă, nu pentru că îi plăcea să ştie foarte multe. Dar a intrat la liceu bun, după acea a intrat la facultate, a terminat facultatea cu 9,96 licenţa, a terminat şi masterul, fără nici o oră de meditaţie, deci se poate şi nu suntem o familie “de genii”, eu am şcoală profesională, tatăl ei doar liceul. (…)
Daniel, Cluj: Cel mai bun răspuns la întrebarea voastră a fost dat de către o fostă Doamnă Secretar de stat în Ministerul Educaţiei care spunea că nivelul subiectelor la Capacitate era de nota 6 pentru cineva care nu face meditaţii; întregul sistem de învăţământ românesc se învârte în jurul meditaţiilor.
VP: Foarte bună observaţia! Adică dacă şcoala, dacă Ministerul Educaţiei spune: “Noi nu vă putem pregăti decât pentru nota 6, la examenele pe care noi le concepem, dacă vreţi mai mult, plătiţi!” Ce tare-i asta! (…)
LP: Lăsând la o parte Limba Română, unde se fac meditaţii pentru a obţine o notă mai bună, pentru a intra la un liceu mai bun, mie mi se pare că fundamentală în problema asta este matematica. Matematica de cele mai multe ori comportă necesitatea unor meditaţii şi astea cred că se întâmplă din următoarele motive: în primul rând că sunt suprapopulate şcolile şi în clasă sunt foarte mulţi copii, în general sunt peste 30, iar matematica e o materie care la un moment dat aştern nişte diferenţe între copii, fiecare cu gradul lui de înţelegere; apoi este şi programa şcolară; este extrem de multă materie la matematică. Deci eu văd: fiu-meu e în pragul examenului şi profesoara lui încă mai are de predat foarte multă materie, când mai sunt două luni până la examen, şi ei ar trebui să recapituleze în perioada asta (…); volumul este foarte mare de materie, diferenţele dintre copii şi numărul de copii din clasă, toate astea duc la probleme cu matematica şi la necesitatea părinţilor …. Mulţi dintre părinţi nu reuşesc … adică eu văd: Oana (soţia lui Luca) care a învăţat foarte bine (…) şi ştie matematică, îl ajută pe fiu-meu şi are momente când şi ei îi este greu, adică ea stă câteva ore să cerceteze anumite probleme şi să-şi amintească cum se făceau ca să poată să-i predea lui fiu-meu, care oricum are şi meditator!
VP: Cel mai bine să ascultăm şi un elev; Ioan e cu noi, bună dimineaţa!
Ioan (clasa a 9-a la SF. Sava): Aici la liceu selecţia a fost făcută foarte bine, aici nu e nevoie de meditaţii, adică poţi să tebazezi 100% pe şcoală, dar la gimnaziu lucrurile stau altfel …
GZ: Dar tu, ca să ajungi acolo ai avut nevoie de meditaţii?
Ioan: Da, asta voiam să vă spun, ca să ajung aici am avut nevoie de meditaţii, dar pentru facultate nu cred că o să am nevoie; la gimnaziu era o dezorganizare totală, la română trebuia să învăţăm tipare pe de rost şi elevii făceau gălăgie la şcoală, nu puteai să te concentrezi. (…) Aici putem să interacţionăm mai mult cu profesorii, se pune accent mai mult pe înţelegere; acolo era pe memorare.
LP: Păi bine mă Ioane, da trebuie să iei în considerare că la Şcoală erai coleg cu copiii “din cartier”, care erau arondaţi acelei şcoli, pe când la liceu, aici, eşti coleg cu nişte oameni care au luat note excepţionale la admitere, pentru că Liceul Sf. Sava din Bucureşti e unul dintre cele unde se intră cu medii de peste 9,80 “sau mai ştiu eu ce”, deci automat acolo ai un colectiv de copii excepţionali.
VP: Cu cât ai intrat la liceu?
Ioan: Cu 9,95!
GZ: Felicitări!
Bogdan: Sunt tatăl unui băiat în clasa a 2-a şi pot să spun cum se văd lucrurile de aici, în sensul că sunt inginer de profesie şi consider că ştiu matematică. Cănd încep să-l ajut pe băiatul meu cu temele la nivelul clasei a doua le facem repede “două mere, trei pere, egal cu cinci, gata, mergem afară!” Dar vine soţia: “nu, n-aţi făcut nimic bine, că-i o întreagă procedură, trebuie nu-ştiu-ce, trebuie nu-ştiu-cum, că altfel nu se punctează nimic”, iar pe mine mă şochează pentru că era important să afli rezultatul, nu mai mult procedura (…). Vă mai dau încă o situaţie puţin extremă, la sport: fiul meu nu este un copil atletic şi am aflat că are probleme la sport, nu ştie să facă genoflexiuni sau cine-ştie-ce trebuie să facă, dar întrebarea a fost: de ce nu este ajutat să facă? (răspunsul a fost): “Da’ ce, să opresc toată clasa?”. Ceilalţi copii sunt toţi sportivi, în sensul că fac toţi sport cu acel profesor.
VP: Da, asta e o problemă profundă a educaţiei din România. Poate că – cine ştie? – cândva se va înţelege că de fapt şcoala este ca să-i ajute pe toţi, şi în primul rând pe cei care au nevoie…
LP: …în primul rând pe cei cu dificultăţi. În Germania, copiii cei mai slabi din clasă sunt aşezaţi în prima bancă şi toată atenţia e pe ăia doi.
VP: Toate modelele de învăţământ nordic sunt centrate pe a-i recupera pe cei care au întârzieri. (…) Apoi, discuţia a luat turnura înspre cei care nici măcar nu ar trebui forţaţi să meargă spre zona de studiu teoretic.
Gigi: (…) Nu trebuie să ajungă toţi 100 din liceul respectiv să dea BAC-ul.
VP: (…) Noi, societatea asta, trăim într-o stare de ipocrizie permanentă. Vrem să demonstrăm în permanenţă că copiii noştri sunt atât de buni încât vor face facultate şi vor ajunge nişte savanţi, nişte învăţaţi. Şi nu găsim un meseriaş, un instalator bun, sau ăia sunt aşa de puţini încât câştigă foarte foarte bine şi toţi îi căutăm prin prieteni etc. Spre deosebire de noi, în Germania de exemplu, plecând de la tradiţia breslelor, a fi meşteşugar, a avea o profesie, a face o şcoală profesională bună este un motiv de mândrie. La noi, la profesională prin tradiţie se consideră că ajung numai “eşecurile”, “loazele”. Ar trebui cumva să schimbăm atitudinea asta, acest mod de abordare a problemei, şi să considerăm că într-adevăr nu toţi vor ajunge savanţi, dar ţara asta are nevoie nu doar de savanţi, are nevoie şi de o mulţime de meseriaşi şi de meşteşugari foarte foarte buni. Există un învăţământ dual, care înţeleg că merge foarte bine (…).
Da, dar asta nu se va întâmpla în România atâta vreme cât pe de altă parte la noi încă ne sună în subconştient vorba din străbuni: “Ai carte, ai parte!”. Aici discuţia a atins o altă cauză a obsesiei naţionale pentru meditaţii, anume strădania părinţilor de a-i ghida pe copii pe o cale cu cât mai puţină muncă, înţelegând prin asta cât mai puţină muncă fizică. Se întâmplă asta pentru că majoritatea românilor nu văd munca intelectuală ca pe o adevărată muncă. Nu se întrevede “la orizont” un reviriment al şcolirii profesionale atâta vreme cât CV-urile trebuie să fie la ora actuală ticsite doldora de cât mai multe diplome înalte şi supraînalte, atâta vreme cât acesta este modelul promovat de către clasa conducătoare: după 45 de ani de comunism, românii au înţeles una şi bună, anume că doar fraierii ajung să facă parte din “clasa muncitoare”, că tu – ca părinte – trebuie să faci tot ce-ţi stă în putinţă să-ţi direcţionezi copilul pe o altă cale decât cea a muncii fizice. Oricum, încheind aici le mulţumesc domnilor din Deşteptarea pentru această dezbatere destul de interesantă pe tema meditaţiilor ajunse la forma unui adevărat sistem de dopaj. CTG. (va urma!)




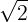 şi pe
şi pe 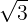 , importanţi pentru elevii de gimnaziu, fiecare cu câte 10 cifre zecimale, imprimate pe treptele ce urcă de la etajul 1 la 2.
, importanţi pentru elevii de gimnaziu, fiecare cu câte 10 cifre zecimale, imprimate pe treptele ce urcă de la etajul 1 la 2.



