În repertoriul meu de activităţi – lecţii formale sau “altfel” – s-au strâns de-a lungul timpului o multitudine de “idei faine”. Unele dintre ele – relativ puţine (~ 10%) – sunt idei personale, total noi; marea majoritate însă sunt colecţionate din diferite surse, iar apoi adaptate nevoilor şi posibilităţilor mele, îmbunătăţite de-a lungul timpului astfel încât efectul lor să fie cât mai bun la clasă.

Un astfel de exemplu îl reprezintă ideea din precedenta postare, idee ce “a stat la dospit” în subconştientul meu cam doi ani, după care a ieşit la suprafaţă sub o formă adaptată. Anul acesta am două clase paralele de a 7-a, aşa încât preocupările mele pentru această clasă sunt duble faţă de anii trecuţi. În aceste condiţii am pus în practică ideea de a aduce numărul π cu multele sale zecimale la propriu pe treptele ce urcă în şcoala noastră spre clasele 7-8, vârste la care avem clar interesul ca elevii să se împrietenească cât mai bine cu acest număr.
Concret, pentru ziua lui π proiectul din acest an a fost următorul: am imprimat pe hârtie A4 autocolantă numărul π cu 50 de zecimale (atâţia elevi sunt în cele două clase); elevii le-au decupat, iar apoi joi, pe 14 martie, le-am lipit pe treptele de la casa scării pe unde urcă elevii de la a 7-a şi cei de la clasele mai mari (până la a 12-a). În plus, “am invitat la petrecere” şi pe cei “doi prieteni” ai lui π, anume pe 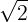 şi pe
şi pe 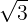 , importanţi pentru elevii de gimnaziu, fiecare cu câte 10 cifre zecimale, imprimate pe treptele ce urcă de la etajul 1 la 2.
, importanţi pentru elevii de gimnaziu, fiecare cu câte 10 cifre zecimale, imprimate pe treptele ce urcă de la etajul 1 la 2.

Pentru imprimare am ales o hârtie autocolantă mai lucioasă, cu speranţa ca cifrele respective să reziste acolo măcar o săptămână (şi, da, după o săptămână sunt tot acolo, deşi treptele au fost spălate zilnic şi jumătate de şcoală “le-a călcat în picioare”). La decupare am avut grijă să rămână la fiecare cifră integru şi restul colii corespunzătoare (partea dreptunghiulară din exteriorul suprafeţei cifrei, sau, cum i-am spus noi, “negativul”, inclusiv interiorul cifrelor 0, 4, 6, 8, 9), astfel încât tehnic am obţinut două seturi de astfel de “abţibilduri”, unul pentru anul acesta şi încă unul pentru viitor. Mai mult, pentru a îmi uşura păstrarea, cât şi pentru a le aduce “pe picior de egalitate”, am decis ca la cifrele cu găuri să folosesc anul acesta mai mult “negativul” şi să păstrez pentru viitor cifra în sine (în afara unor excepţii). Am obţinut astfel un model jucăuş, mult mai atractiv decât o simplă succesiune de cifre.
În plus, faţă de o simplă şi monotonă succesiune de cifre, dar şi pentru eficienţă financiară a acţiunii, am imprimat primele cifre pe o anumită mărime, iar apoi pe mărimi tot mai mici (deci tot mai multe pe o coală A4). Astfel, pentru tot proiectul am avut nevoie de doar 21 de coli imprimate (pentru care am plătit cca. 26 de lei la firma Colorama din Cluj). Ca să nu încurc cifrele în procesul de imprimare şi decupare cu diferiţi elevi, a trebuit să-mi fac un sistem de poziţionare a fiecărei cifre (deşi am oarece dubii că totul este corect, pentru că am rămas cu un 8 în plus; asta e!).

Pe viitor, când voi decide să folosesc al doilea set, pentru că nu va mai fi nevoie de decupat, elevii respectivi vor putea primi alte “sarcini” de implicare, de pildă să coloreze cifrele (sarcină “dificilă” din punct de vedere matematic; americanii fac faze din acestea, reuşind să implice în activitatea matematică şi elevii non-matematicieni; de pildă să aducă cu ocazia acestei zile “pi-scuiţi”, adică biscuiţi neapărat rotunzi etc.). Apropos: a fost foarte interesant faptul că un elev cu CES s-a implicat foarte intens în dezlipirea foliei de pe spatele cifrelor şi apoi lipirea acestora pe ciment; era clar că odată ce-a prins mişcarea îi plăcea respectiva activitate repetitivă; eu am fost bucuros că în sfârşit am reuşit să cobor până la nivelul lui “în ora de matematică”, în afară de simpla copiere de pe tablă a lecţiei de zi cu zi. Acum am un argument în plus în faţa clasei că “îl trec”, că îi dau 5-ul.
Pe lângă această activitate, în funcţie de disponibilităţi se poat face şi altele (proiecte individuale de afişat pe pereţi etc. Pentru cei ce doriţi să preluaţi ideea, ataşez prezentei postări şi documentele pe baza cărora s-au imprimat respectivele cifre, cu cele 21 de pagini A4 (atenţie că cei doi radicali au cifrele “combinate” pe mărimi şi trebuie separate corect). CTG P.S. În weekend-ul următor am avut acasă şi un tort de ziua lui π.

Zipped-PiRad2.3.zip


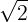 şi pe
şi pe 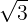 , importanţi pentru elevii de gimnaziu, fiecare cu câte 10 cifre zecimale, imprimate pe treptele ce urcă de la etajul 1 la 2.
, importanţi pentru elevii de gimnaziu, fiecare cu câte 10 cifre zecimale, imprimate pe treptele ce urcă de la etajul 1 la 2.



