Pentru cei care cunoașteți limba engleza, vă recomandăm urmatoarea adresă. Sunt prezente aici gânduri peste care de obicei sărim.
Marvin Minsky – What makes Mathematics hard to learn?
Echipa de redacție
Pentru cei care cunoașteți limba engleza, vă recomandăm urmatoarea adresă. Sunt prezente aici gânduri peste care de obicei sărim.
Marvin Minsky – What makes Mathematics hard to learn?
Echipa de redacție
În toamna anului 1982 eram în clasa a X-a. La o oră de matematică mama mea, care ne era profesoară, a adus la oră şi câteva probleme cu trapeze. După primele două probleme destul de accesibile a venit o a treia care ne-a lovit puternic. Un alt coleg a fost la tablă, aşa că am putut gândi liber. Deşi am relatat de nenumărate ori ce a urmat, acum este prima oară când “aştern pe hârtie” povestea acelei întâmplări memorabile.
Pe scurt, în următoarele minute am descoperit o nouă “formulă pentru aria triunghiului”, o reţetă necunoscută până în acel moment; nici un profesor nu o cunoştea şi aceasta nu se găseşte în nici o carte. În ora respectivă mintea mea a umblat pe unde nu a mai umblat nici o minte de om. Descoperisem “o mică pată albă” pe întinsa hartă a matematicii, iar aceasta nici măcar nu era la periferie, ci se afla în zona centrală, elementară a matematicii, zona pentru elevi.
Iată în continuare cele trei probleme şi evoluţia gândurilor mele din acea oră.
Imaginea prezentată este o scanare din culegerea De la Cercul lui Thales la Moneda lui Ţiţeica, C. Titus Grigorovici, Mariana Grigorovici, publicată în 2006 la Humanitas Educaţional. În culegere am schimbat ordinea problemelor faţă de cea din ora respectivă.
După cum am spus, demonstraţiile primelor două probleme mi s-au părut accesibile; chiar am avut atunci o senzaţie de frumos în acele momente, probabil şi datorită faptului că reprezentau o îmbinare de geometrie şi algebră.
1) Având aceaşi bază şi înălţimile egale, ΔADC şi ΔBDC au aceeaşi arie. Din egalitatea celor două scădem porţiunea comună, aria ΔODC, obţinănd egalitatea ariilor ΔAOD şi ΔBOC. Nu am în amintire cum s-a scris rezolvarea pe tablă, dar ştiu cum am scris-o eu:
2) Trasând linia mijlocie [MN] observăm că ΔBMN şi ΔCMN au aceeaşi arie, având baza comună şi înălţimile egale (cât jumătate din înălţimea trapezului). Obţinem astfel:
AriaΔMBC = AriaΔBMN + AriaΔCMN =
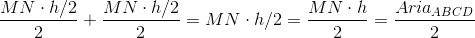
3) La a treia problemă lucrurile nu arătau deloc la fel de frumos, în primul rând pentru că rezolvarea previzibilă era cu asemănare de triunghiuri; era o rezolvare lungă şi istovitoare. Nu aveam nici un chef de aşa ceva; se prevedea o demonstraţie urâtă în comparaţie cu precedentele. Ei, şi atunci mintea mea a început să lucreze, observând anumite coincidenţe:
– triunghiurile echivalente din prima problemă apăreau şi aici;
– cele două triunghiuri echivalente stăteau ambele înclinate, într-un colţ; la fel şi triunghiul MBC din problema a doua (triunghiurile stau de obicei pe bază, nu înclinat);
– triunghiul MBC din a doua problemă are aria egală cu semiprodusul “orizontalei” prin M cu înălţimea totală a triunghiului, adică “diferenţa de nivel” între B şi C;
– cele două triunghiuri echivalente din prima problemă au aceeaşi înălţime totală, adică “diferenţa de nivel” între vârful de la baza mică şi cel de la baza mare a trapezului, iar cerinţa spune că “orizontalele” prin vârful intermediar ar trebui să fie egale;
– avem deci trei mărimi care se pare că depind una de cealaltă: aria unui astfel de “triunghi răsturnat”, apoi “înălţimea totală” a triunghiului, adică “diferenţa de nivel” între vârful situat cel mai jos şi vârful situat cel mai sus, iar pe post de bază “orizontala” prin punctul intermediar până la latura opusă.
Dacă reuşeam să demonstrez că aria unui triunghi ce este poziţionat înclinat, adică neavând baza aliniată pe “orizontala” figurii, aria unui astfel de triunghi respectă modelul tradiţional de baza ori înălţimea pe doi, atunci era rezolvată problema 3). De aici lucrurile au mers uşor: mi-am făcut o figură separată pentru “teorema” ce-o doream demonstrată, am descompus triunghiul mare în două pe baza “orizontalei”, m-am jucat puţin cu factorul comun şi VOILA!, gata era teorema mea.
Desigur, rezolvarea mea era mai scurtă şi datorită faptului că fentasem, folosind rezultatul primei probleme drept cunoscut. Oricum însă, terminasem cu câteva minute bune înaintea colegului de la tablă, care se chinuia împreună cu maică-mea printre rapoarte şi triunghiuri asemenea. Iar eu eram literalmente în al nouălea cer, având în plus şi o teoremă şmecheră în buzunar!
Este uşor de închipuit cum am stat “ca pe ace” ca să se termine demonstraţia stupidă de la tablă şi cu aceasta şi ora, ca să fug la mama – pardon, la Tovarăşa Profesoară – să-i prezint isprava mea.
O singură întrebare mai rămâne de lămurit: de ce a ales mama cele trei probleme în această succesiune? Prima şi a treia au cam aceeaşi figură; a doua se integrează şi ea cumva. Nu ştiu ce să zic, dar momentul a fost superb.
Titus Grigorovici
Ia priviţi ce imagine minunată am găsit pe pereţii unei clase, la o învăţătoare de la o şcoală “de centru” din Cluj. Habar nu aţi avut voi, dragi profi de mate, cum se face împărţirea la zero!
Ei, acuma ştiţi! Dacă n-ar fi de plâns, atunci ar fi de râs!!!
Se pare că cei de la editura cu pricina s-au prins de gafă: afişul existent actualmente în oferta lor nu mai conţine şi împărţirea la zero. Rămân doar gândurile despre cum s-a putut aşa ceva, de ce este nevoie ca elevii să înveţe pe dinafară tabla împărţirii (vezi citatul din Eugen Rusu cu ştiutul pe dinăuntru), cum de învăţătoarea respectivă nu şi-a dat seama de greşeală (şi cine ştie câte astfel de afişe or fi atârnând prin clasele patriei noastre) etc.
Gaşca cu poza
Eseu în legătură cu tema
Gândirea aritmetică vs. gândirea algebrică
Un aspect deosebit al adaptării lecţiilor la posibilităţile intelectuale ale elevilor, mai exact la posibilităţile Elevului, luat ca elev mediu, ca eşantion reprezentativ al clasei – nu ca eşantion de vârfuri, cu care să ne lăudăm cu rezultate la olimpiade, un aspect al acestei adaptări este faptul că dacă nu o facem noi, atunci elevii “ne taxează”, găsind ei scurtături, de obicei greşite, în raţionament, “shortcut-uri” care scurt-circuitează strădaniile noastre de a le forma o gândire matematică corectă. Cu alte cuvinte, dacă nu adaptăm noi lecţia la nivelul lor – noi am face-o corect – atunci o fac ei, şi de cele mai multe ori ei o fac greşit, inventând reguli care sunt în general false.
De curând am găsit un exemplu flagrant în acest sens: un elev de clasa a V-a pe care l-am întrebat cum a făcut exerciţiul de la lucrare cu comparare de puteri (era desigur un exerciţiu cu două puteri care nu aveau nici aceeaşi bază, nici acelaşi exponent, aşa cum cere în programă; dar cele din programă sunt banale; pentru olimpici avem nevoie să sărim peste programă şi să folosim o formulă ce este trecută actualmente la începutul clasei a VI-a; s-ar putea imagina desigur şi o rezolvare fără formula respectivă, dar oricum nu respectă programa).
Răspunsul elevului a fost bulversant: exerciţiul acela a fost uşor: puterea cu baza mai mică şi exponentul mai mare, aia este mai mare! (am citat cuvânt cu cuvănt, pentru că l-am notat imediat pe o hârtiuţă).
Este evident că pe viitor voi avea mare grijă să aleg la aceste exerciţii – în clasa a VI-a – un număr egal de exemple pe ambele variante şi voi avea în plus grijă să-i şi atenţionez să nu inventeze vreo regulă de scurtătură. Pentru asta mi-am pregătit câte trei exemple din fiecare (cu câştigătorul cu baza mai mare, respectiv cu baza mai mică), pe care să le dau la clasă, ca să fiu sigur, independent de ce oferă autorii culegerii după care lucrăm la teme. Iată cele şase exemple:
1) Exemple la care este mai mare puterea cu bază mai mare:
233 < 322 pentru că 23 < 32 (8 < 9)
636 < 1524 pentru că 63 < 152 (216 < 225)
721 < 1914 pentru că 73 < 192 (343 < 361)
2) Exemple la care este mai mică puterea cu bază mai mare:
514 < 321 pentru că 52 < 33 (25 < 27)
515 < 235 pentru că 53 < 27 (125 < 128)
355 < 288 pentru că 35 < 28 (243 < 256)
Căutând un motiv pentru care elevul nostru a apelat la o astfel de “regulă” de scurtătură, îmi imaginez doar că mintea sa a încercat să gândească ce se întâmplă la exerciţiile de la clasă, dar gândirea sa nefiind trecută de la nivelul aritmetic la cel algebric, gândirea sa deci a avut impresia că “observă o regularitate”, iar atunci, în acel moment s-a simţit în posesia adevărului, reţinând ideea respectivă drept regulă.
Titus Grigorovici
Mai deunăzi urmăream la televizor un concurs de sărituri cu schiurile de la trambulină. Totul decurgea cum nu se poate mai bine, erau în manşa a doua a concursului, săritorii zburau tot mai mult, tensiunea creştea iar comentatorul se străduia să redea cât se putea de bine starea de spirit din jurul trambulinei. La un moment dat comentatorului nu i-a mai ajuns vocabularul normal şi a apelat la amintirile vagi ce le mai avea din copilărie: cutare săritor, ne aşteptăm să primească note bune de la juriu, pentru că a aterizat foarte bine, cu schiurile coplanare!
Era să mă apuce sughiţu’: oare cum ar fi să aterizeze un schior cu schiurile necoplanare? N-aş vrea să văd aşa ceva! Concurentului respectiv îi fugise piciorul drept un pic în exterior, iar comentatorul a vrut probabil să exprime că schiurile au fost la aterizare aproape paralele, cu un defect neglijabil. Ce a ieşit pe gură, ne arată însă ceaţa deasă ce se aşterne după ani şi ani asupra cuvintelor “turnate cu tolceriu” în mintea elevilor, fără ca aceştia să le înţeleagă cu adevărat. Pentru că un lucru este clar: ce ai înţeles cu adevărat nu se va putea întoarce niciodată greşit, sub forma unei astfel de perle.
Ce dată credeţi că este prezentată în scrierea de mai jos?
(2□)Δ.1Δ.3Δ∙(2□)□∙(3Δ)Δ
Nu vă speriaţi! Nu este nimic greşit în transcrierea textului pe aparatul dvs. M-am jucat doar un pic cu notaţiile, de obicei atât de uzuale în matematică.
Astfel, prin 5Δ am notat numărul triunghiular 15 = 1 + 2 + 3 + 4 + 5.
În mod similar, am notat de data asta cu 5□ numărul pătrat 25 = 5 ∙ 5 = 52.
Vă las ca o scurtă temă de cercetare să aflaţi ce sunt acelea numere triunghiulare şi cum se reprezintă ele grafic, dar şi cum apar ele în materia obişnuită de clasa a V-a. Dacă vă străduiţi puţin veţi găsi că am trecut acolo nimic mai mult decât ultima zi din această vacanţă de iarnă.
Interesant că la toate clasele sa manifestat o mare nedumerire în legătură cu punctuleţele de jos. Ce înseamnă acestea? Era foarte interesant că nu se ocupau de ceea ce ştiu, ci tot întrebau despre aspectele neînţelese.
Oricum, rămân în urma primei zile de şcoală cu amintirea unor zâmbete entuziasmate din parte elevilor care au reuşit să traducă până la capăt, înţelegând astfel şi ce-i cu punctele acelea de jos.
Cei care au terminat mai repede au primit şi un bonus, anume să descifreze şi următoarea “minune”:
210 + 29 + 28 + 27 + 26 + 25 = 2016
Cei extrem de harnici au primit “de descifrat” şi anul precedent, a cărui scriere este la fel de ciudată:
210 + 29 + 28 + 27 + 26 + 24 + 23 + 22 + 21 + 20 = 2015
*
Prima zi de şcoală reprezintă întotdeauna o ciudăţenie. Pe de-o parte o urăşte toată lumea, aici fiind unul din puţinele momente când sunt de acord şi elevii şi profesorii. Pe de cealaltă parte, reîntâlnirea cu colegii şi prietenii reprezintă pentru mulţi un moment de bucurie.
Pentru a intra cât de repede în procesul matematic, dar a nu prezenta prin aceasta un şoc elevilor, eu obişnuiesc să le aduc în prima oră de matematică o problemă distractivă, o întrebare cu tâlc, care nu trebuie să aibă de-a face neapărat cu materia la zi sau cu cea parcursă înainte de vacanţă. Acestea au întotdeauna efectul de a afişa pe faţa elevilor o stare de bucurie amestecată cu uimire, stare pe care apoi o folosesc pentru a intra în matematică cu optimism (desigur, cât de bine merge de la un elev la altul). Anul acesta am adus întrebarea de mai sus, cu descifrarea căreia am petrecut câteva clipe interesante. Întrebarea este foarte bună şi potrivită deoarece:
Oricum, La mulți ani! 2016
Titus Grigorovici