Elevul de gimnaziu este confruntat constant cu elemente de matematică peste nivelul intelectului său, peste posibilităţile sale de asimilare sau peste capacităţile sale de înţelegere. Acest curent de predare a fost introdus în România prin reforma şcolară din 1980, nivelul fiind atunci reglat după elevii de vârf, lăsând “în offside” intelectual marea majoritate a populaţiei şcolare. Dacă până atunci “lungimea de undă” a nivelului matematicii şcolare era stabilită conform nivelului elevilor medii, a marii mase a elevilor, a celor reprezentând corpul central din “Clopotul lui Gauss”, după acel moment reformă nivelul materiei şi a aplicaţilor au fost trase agresiv înspre dreapta, înspre copiii cu un coeficient de inteligenţă mai ridicat, spre marginea zonei coeficientului de inteligenţă obişnuită, chiar trecând pragul deseori în zona cunoscută generic ca a persoanelor superinteligente. Chiar mai mult, uneori cunoştinţe diverse sunt aduse în faţa claselor fără ca măcar şi o persoană superinteligentă să poată înţelege, asta dacă nu apelează la informaţii suplimentare, sau la propria intuiţie ieşită din comun (fie aceasta de nivel algebric sau geometric).
Alteori elevii primesc informaţii practic accesibile, dar pentru înţelegerea cărora le lipsesc diverse alte informaţii pe care primele au nevoie să se sprijine. Efectiv li se predau anumite lucruri pe baza altora care însă nu au fost prezentate. Aceasta reprezintă o gafă inacceptabilă în predarea matematicii, care însă totuşi se întâmplă din când în când. În această miniserie mi-am propus să abordez trei astfel de exemple în care diferite elemente matematice sunt predate mult prea devreme pentru nivelul elevilor sau pentru nivelul cunoştinţelor deja însuşite, sau în forme mult prea elevate pentru o primă abordare, respectiv pentru abordarea din clasele gimnaziale.
Dar, de unde această preocupare? Sau, care a fost “scânteia” pentru acest demers? Prin toamnă “mi-au ajuns la ureche” câteva lecţii de geometrie în clasa a 6-a, în care vedeam clar că un coleg sau o colegă au dificultăţi mari în a selecta ce cunoştinţe despre cerc să fie aduse în faţa elevilor cu această primă ocazie. Situaţii similare am întâlnit legat de partea de cerc din toamna clasei a 7-a, ce implică aspecte ce se bazează pe materie încă neparcursă. Iniţial am pornit un articol ţintit în această direcţie – a predării cercului, dar destul de repede mi-am dat seama că putem studia problema la un nivel mai general, anume al impulsului dascălilor de a face mai mult decât pot duce elevii în acel moment, fie din punct de vedere al dezvoltării intelectului, fie datorită faptului că sunt implicate elemente încă nestudiate, fie alteori pur şi simplu datorită unei cantităţi mult prea mare de informaţii aduse într-o lecţie. Aşadar, să vedem ce astfel de exemple am adunat din predarea actuală a cercului în clasele gimnaziale.
*
De foarte mulţi ani cercul nu apărea în viaţa elevilor decât în clasa a 7-a, chiar spre finalul clasei, iar profesorii s-au obişnuit să aducă cunoştiinţele despre cerc într-o anumită formă şi mai ales “toate la pachet”. Acum, când informaţiile despre cerc au fost despărţite prin noua programă, colegii au uneori dificultăţi în a le separa coerent şi cu sens. Pentru că – desigur – nimeni nu stă toată ziua cu programa sau cu planificarea “sub nas”, amintirile şi obiceiurile de ani buni preluând uneori controlul “turuirii” lecţiei.
Astfel, conform programei din 2017, în clasa a 6-a apar un prim set de cunoştinţe elementare prin “semestrul I”. Un alt set de cunoştinţe, mai elevate, au fost mutate în toamna clasei a 7-a, iar ultimele elemente au rămas în finalul acestei clase. Desigur că programa oficială poate fi considerată destul de clară în acest sens, dar “mentalul” unor profesori le joacă feste, iar aceştia scapă în lecţiile de a 6-a sau în cele de a 7-a din toamnă puţin prea mult, adică elemente ce încă nu pot fi înţelese de către elevi (din diverse cauze).
Pe de altă parte, poate că nici programa nu precizează conţinuturile destul de clar pentru unii, lăsând astfel loc profesorilor pentru realizarea unor momente în care lecţia “îi năuceşte” pe elevi. Cu totul, am impresia unei forme insuficient lămurite, care duce direct sau doar lasă loc unor situaţii în care elevii sunt confruntaţi cu situaţii de tipul “prea devreme”.
Să analizăm câteva exemple. Primul moment de bulversare pare a fi tangenta la cerc, inclusă în programă sub titlul Poziţiile unei drepte faţă de un cerc. Trebuie făcută aici proprietatea că tangenta este perpendiculară pe raza în punctul de contact, sau nu trebuie făcută? Nu-i clar, programa lăsând lucrurile la cheremul interpretării fiecărui profesor.
Dar, dincolo de orice discuţie, sigur n-ar trebui să apară aici, în toamna clasei a 6-a, proprietatea de congruenţă a celor două tangente dintr-un punct exterior la un cerc. Aceasta se subînţelege destul de clar din titlul tangente dintr-un punct exterior la un cerc, din clasa a 7-a. Cel mai rapid moment de a parcurge această informaţie ar fi în primăvara clasei a 6-a, ca aplicaţie la congruenţa triunghiurilor dreptunghice. Totuşi, parcă în clasa a 7-a “îi şade mai bine”.
Dar, sigur-sigur nu are ce căuta în clasa a 6-a unghiul înscris în cerc! O spun atât de apăsat, pentru că, din păcate, mi-a fost dat să văd şi aşa ceva. Nici nu are rost să discutăm aici acest exemplu. Punct!
Dar şi în toamna sau iarna clasei a 7-a mi-a fost dat să văd ciudăţenii ce sfidează logica ordonării matematicii. De vreme ce a fost adus “în semestrul I” un pachet despre poligoane regulate, desigur că au fost şi colegi care au început să aducă lecţiile despre triunghiul echilateral şi pătrat, implicând formulele respective pline de radical din 2 sau din 3, formule ce necesită însă experienţa şi deducerea pe bază de trigonometrie. Cele trei lecţii – formulele din triunghiul echilateral, pătrat respectiv hehagonul regulat – acestea îşi au clar locul în finalul clasei a 7-a. Faptul că acest calup încă este ataşat de titlul mare de poligoane regulate nu este decât parţial justificat (am tratat subiectul pe larg în postarea precedentă). Asta arată cât de neclară este impresia generală despre ce vrea acest titlu, poligoane regulate, anume că există de fapt două lecţii separate la care a fost folosit.
Prima ar fi studiul fenomenului despre poligoane regulate în general, ce trebuie făcut pe baza a câteva exemple suficient de edificatoare (despre acestea în sine ca fenomen, construcţia lor, dar şi despre unghiurile acestora), cu o trecere spre final în cazul general (acest moment trebuie conectat cumva şi cu suma unghiurilor unui poligon neregulat). Partea cu construcţia este extrem de neglijată de colegi în general (desenaţi cu instrumentele un nonagon regulat; care se pot desena cu ajutorul raportorului; care se pot desena fără raportor, doar cu liniar şi compas?).
A doua lecţie este despre primele trei cazuri particulare – triunghiul echilateral, pătratul şi hexagonul regulat – şi care nu are mare lucru de-a face cu prima parte decât poate “tangenţial”, acestea fiind într-adevăr nişte poligoane regulate. Aici accentul se pune mai ales pe lungimile diferitelor segmente implicate, în formate raţionale sau iraţionale (prin apariţia radicalilor din 2 sau din 3). Această a doua lecţie este profund necesară în clasa a 8-a la calculele corpurilor cu astfel de baze. Ca urmare, este evident că s-ar potrivi mult mai bine la începutul clasei a 8-a, cu aplicaţii imediate pe diversele corpuri, dar “face sens” să o parcurgem şi în finalul clesei a 7-a, astfel încât elevii să o vadă, iar apoi în a 8-a elementele respective să fie aduse o a doua oară, ca recapitulare (drept cunoştinţe vechi). Probabil din comoditate, pentru a nu se tot scrie toate cele trei denumiri, s-a folosit şi la acestea titlul mare de poligoane regulate. Totuşi, cred că mult mai cinstit ar fi poligoane regulate particulare (deşi nici acesta nu-i perfect).
Cam aceasta este şi părerea programei oficiale, care spune în cadrul capitolului 5. despre cerc din a 7-a: Poligoane regulate înscrise într-un cerc (construcţie, măsuri de unghiuri). Apoi, în capitolul 7 cumulând relaţiile metrice în triunghiul dreptunghic, cu teorema lui Pitagora şi cu trigonometrie, la rezolvarea triunghiului dreptunghic apar în paranteză: (latura, apotemă, arie, perimetru) în triunghiul echilateral, în pătrat şi în hexagonul regulat … Deci, prin programa nouă nici nu se mai face referire la poligoane regulate, dar unii colegi încă n-au realizat diferenţa.
*
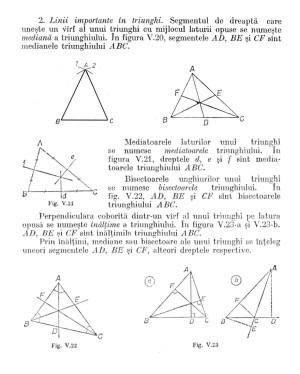
Multe s-ar mai putea discuta pe astfel de exemple legate de predarea cercului, dar eu am deschis acest subiect având în gând un aspect mult mai discutabil. Este vorba despre conectarea cu subiectul cercului la lecţia despre liniile importante în triunghi. Aici cele cerute prin programă sunt clare: Linii importante în triunghi: bisectoarele unghiurilor unui triunghi: concurenţa (fără demonstraţie), cercul înscris în triunghi; mediatoarele laturilor unui triunghi: concurenţa (fără demonstraţie), cercul circumscris unui triunghi etc. Deci, apar clar prezente în programă existenţa celor două cercuri, cercul înscris în triunghi, respectiv cercul circumscris unui triunghi. Nu apare însă prezentat defel ce ar trebui să se întâmple cu acestea. De pildă, trebuie explicate şi folosite la ceva? Că demonstraţia pare că nu este necesară (deşi în cazul elevilor inteligenţi acest raţionament chiar ar merita făcut.
Legat de lecţia despre liniile importante în triunghi, am impresia că aici apare din nou un moment din acela în care noi ne pornim să le dăm un anumit set de informaţii elevilor şi ne trezim fără să ne dăm seama că le turnăm mult prea multe altele, încărcându-le mintea şi anulând percepţia informaţiilor de bază prin încărcarea cu altele mai grele.
Care ar fi aici informaţiile de bază? Păi, în primul rând cele patru tipuri de linii importante (două cunoscute deja, însă nu în contextul unui triunghi, dar şi două total noi). Apoi, apare ideea că din fiecare tip există chiar trei bucăţi (deci 12 cu totul). O provocare uriaşă, pentru cei mai mulţi elevi chiar o provocare insurmontabilă, o reprezintă faptul că desenele corespunzătoare celor patru tipuri de linii importante seamănă foarte mult între ele. Marea majoritate a elevilor nu au în acel moment capacitatea să vadă deosebirile dintre acestea.
La desenarea acestora trebuie făcută o construcţie exactă, iar asta este pentru cei mai mulţi elevi în clasa a 6-a o mare provocare. Ca profesor, a te aştepta că elevii vor înţelege doar pe baza unor desene făcute în grabă (de obicei incorecte în caiete) şi însoţite de nişte definiţii dictate, asta înseamnă că te îmbeţi cu apă chioară. Chiar şi dacă unii vor şti eventual să-ţi turuie definiţia, asta nu înseamnă că aceştia cunosc şi au înţeles fenomenul.
Dacă nu se fac desenele, sigur nu se înţelege nimica din toată lecţia; nu vreau să susţin aici că un elev care are desenele cât de cât corecte a şi înţeles automat lecţia. În cazul unor desene corecte, destul de repede se observă cocnurenţa celor trei linii de un fel, iar asta poate reprezenta un gând deosebit, dar şi o informaţie suplimentară (depinde cum reuşeşti să le-o aduci). Apropos de asta, eu am pus la punct un sistem prin care elevii chiar ajung să îndrăgească această lecţie (“Ce frumos!!!”), dar asta ia ceva mai mult timp.
Revenind la ce văd elevii şi cum desenează în caietele lor, toţi observă clar concurenţa şi fac desenul ca atare, dar ei nu respectă de obicei corectitudinea construcţiei liniilor. De pildă, de obicei la înălţimi vom vedea în caiete înălţimea verticală pe bază (perpendiculară, dar nu datorită folosirii echerului, ci prin simpla trasare a unei verticale), dar celelalte două înălţimi, cele oblice, nu vor fi de obicei perpendiculare pe laturile opuse. Toate trei vor fi însă concurent desenate, ceea ce ne spune mullte despre “ce văd elevii”. La bisectoare se prea poate să întâlnim desene fără nici măcar o bisectoare adevărată. La fel şi la mediatoare. Doar la mediane cresc puţin şansele să găsim un desen corect, dar nu neapărat.
Pe lângă aceste deja multe informaţii din lecţia de bază, ar mai trebui discutată şi situaţia specială a triunghiului obtuzunghic, care are două înălţimei exterioare, şi la care înălţimile, dar şi mediatoarele se întâlnesc în exteriorul triunghiului.Cred că aceste situaţii se pot lăsa liniştit pe altă oră, sau date ca temă specială pentru elevii buni. Cu toată clasa pot fi lăsate poate chiar pe începutul clasei a 7-a, în zona de recapitulare şi completări.
Da, iar acum înţelegem absurdul situaţiei, faptul că o astfel de lecţie deja mult prea încărcată (pe care probabil cei mai mulţi profesori o parcurg într-o oră, sau chiar sub o oră), se cere să o supraîncărcăm cu noi informaţii, care desigur că se potrivesc cumva aici, dar sunt prea multe şi prea grele!
Astfel. ortocentrul este cel mai inofensiv, pentru că nu este nimic special în spatele acestui nume, dar deja la centrul de greutate trebuie să le explici pe scurt ce-i acela un centru de greutate (deşi acesta are clar de-a face cu proprietăţile ariei ce se studiază de-abia în a 7-a).
Cât despre cercul înscris sau cel circumscris, pe cei mai mulţi elevi “i-ai trminat” cu acestea! Chiar şi dacă ar avea experienţă suficientă de construcţii cu compasul, şi tot ar fi greu pentru cei mai mulţi. Dar ţinând cont că nu se lucrează aproape defel cu compasul la clasă (până în acel moment), aceste construcţii le apar elevilor ca nişte “monştrii”; ei efectiv le percep “terorizante”.
Fac aici o paranteză, încercând să explic ce se întâmplă de obicei în clase în momentul puţinelor construcţii cu instrumente, realizate pe tablă de către profesori. Părerea mea este că majoritatea colegilor nu le îndrăgesc, nu le stăpânesc şi le fac minimal, “că se cere în programă”. Din păcate însă, la construcţiile cu instrumente, trebuie petrecut foarte mult timp cu elevii, astfel încât aceştia să le şi stăpânească. Majoritatea elevilor nu le vor înţelege din prima, aşa încât fiecare desen trebuie făcut de cel puţin două ori (după 5-6 construcţii pe o schemă ne putem baza că majoritatea elevilor le-au înţeles şi le pot face). În plus, dacă atunci când face o anumită construcţie, profesorul stă în faţa tablei, cu spatele la elevi, cei mai mulţi nu vor vedea ce face acesta. Iar apoi acesta se miră de ce nu ştiu elevii.
Ca tehnică, eu personal procedez astfel: fac întâi un desen pe tablă încercând să explic cât de bine, dar fără pretenţii de a avea o largă pricepere din partea elevilor. Când mă dau de-o parte desigur că văd o mare de priviri perplexe de felul “da’ cum aţi făcut asta?”. În acest context primul desen apare doar ca o prezentare a ce urmează să fie învăţat, nimic altceva. Le-o mai explic o dată din lateral arătând cu mâna cele explicate, după care mai fac o dată desenul încet, încercând să stau cât mai în lateralul figurii, sau să mă dau de-o parte după fiecare mic pas de construcţie, astfel încât elevii să vadă exact ce fac şi cum manevrez instrumentul (desenatul liniilor drepte cu liniarul este uşor, dar deja compasul, echerul şi raportorul ridică mari probleme şi folosirea lor trebuie foarte mult repetată şi exersată până când este stăpânită de către elevi; nu discut aici despre măsuratul lungimilor de la capătul liniarul sau de la 1).
Totuşi, experienţa îmi arată că în ora următoare mai trebuie să fac încă o dată “arătatul construcţiei” pentru câţiva, şi apoi doar încă peste o oră am dreptul să mă aştept că elevii se vor descurca la acel desen. Chiar şi aşa, dacă am nevoie de această construcţie peste 2 săptămâni, deja mă pot aştepta ca unii să se uite cu disperare că nu mai ştiu “cum se face”. Situaţia este una dificilă, foarte mare consumatoare de timp, astfel încât – revenind la subiectul nostru – cu greu ne putem aştepta ca într-o oră să avem în caiete cele patru desene cu liniile importante realizate corect, darămite să mai apară acolo cât de cât corect desenate şi cele două cercuri din titlul acestui articol.
Revenind la cercul înscris, respectiv la cercul circumscris, părerea mea este că cele două cercuri fac parte dintr-o altă lecţie, care se potriveşte mult mai bine în clasa a 7-a. La fel desigur şi centrul de greutate. Deci, concluzionând, noi în loc să-i lăsăm pe elevi să priceapă lecţia de bază – cele patru ori trei linii importante în triunghi – noi repede le mai turnăm şi începutul unor lectii ulterioare, potrivite mai degrabă peste jumătate de an, după ce a mai avut loc o perioadă de sedimentare şi de dezvoltare, prin acumulare de experienţă suplimentară. Uau, ce ne pricepem să chinuim copiii!
Revenind la ideea că cele patru desene (fiecare cu câte trei linii de un fel, concurente) sunt fiecare în sine foarte grele, practic inaccesibile în viteză majorităţii elevilor, este minunat că măcar nimeni nu se gândeşte să le facă pe toate într-un singur triunghi. Cred că nimeni nu le face pentru că el în sine ca profesor nu ar fi în stare să le facă.
Bun, şi ce ar trebui să facem? Pentru că – staţi liniştiţi – şi eu sunt de obicei tentat să le spun copiilor cum se numesc acele patru centre de concurenţă (aşa încât prezentul eseu reprezintă nu doar unul de critică la adresa colegilor, dar şi unul de autocritică, de autoanaliză). Mai ales în condiţiile actualilor elevi, post-pandemici, adică post-online, cu o capacitate de atenţie asupra detaliilor muuult scăzută faţă de ce cea cu care eram obişnuiţi până în 2019, eu chiar cred că ar trebui să lăsăm denumirile respective pe altă dată.
Pe când? Poate pe când urmează acestea să fie folosite împreună cu restul materiei cu care se potrivesc (de pildă centrul de greutate în capitolul despre arii din clasa a 7-a). Sau poate, cele două cercuri – înscris respectiv circumscris – ar putea fi lăsate pe începutul clasei a 7-a, cu refacerea desenelor şi împreună cu cercul corespunzător în cadrul primelor ore de recapitulare din septembrie.
Sau poate, o variantă interesantă ar fi să reluăm lecţia ora următoare, dar de data asta şi cu denumirile corespunzătoare, inclusiv cu desenarea celor două cercuri (la desenul bisectoarelor, respectiv la cel al mediatoarelor). Această variantă ne-ar asigura o formă “mai umană” a lecţiei, însă cu respectarea programei. Merită să pierdem pentru asta încă o oră? Pentru înţelegerea copiilor, eu cred că da (fiecare cu părerea lui).
Totuşi, eu personal înclin să aleg varianta cu aducerea celor două desene cu cercuri (înscris, respectiv circumscris triunghiului) în cadrul capitolului despre cerc din clasa a 7-a. Acolo ar avea cel mai mult sens să fie incluse. Însă şi aducerea acestora în clasa a 6-a, în zona aplicaţiilor la studiul metodei triunghiurilor congruente ar avea sens (destul de repede după lecţia despre linii importante).
Dar, cum ar arăta atunci prima lecţie, cea în care să nu amintim denumirile punctelor de concurenţă? Am găsit în manualul lui Hollinger din 1977 ce l-am avut noi în clasa a 6-a, cum se făceau acestea atunci. Astfel, în imaginea următoare vedeţi cum era prezentată această lecţie ca parte din lecţia despre triunghiul isoscel (nu mă întrebaţi de ce era pusă acolo, că nu-i găsesc o logică clară). Oricum, vedem că Hollinger nu amintea în acel moment nici măcar ideea de concurenţă (acest cuvânt apărea prima dată peste două pagini, în cadrul unei lecţii cu titlu Probleme rezolvate, la prima astfel de problemă, practic la analizarea medianelor într-un triunghi isoscel, acolo unde într-o paranteză se spune că medianele sînt concurente; nici vorbă însă să-l şi denumească pe acest punct de concurenţă!).
În textul de mai sus nu se aminteşte concurenţa, dar aceasta este clar prezentă în figurile corespunzătoare. Astfel, în plus faţă de forma din lecţia lui Hollinger, eu cred că totuşi putem să le atragem atenţia că cele trei linii de un fel sunt concurente (elevii oricum văd chestia asta, deci doar vor învăţa acest cuvânt ataşat cu sens unei situaţii). Dar oricum, eu de acum în colo nu voi mai denumi aceste puncte din prima lecţie, nici măcar nu le voi mai nota (cu renumitele H, G, O, I), darămite să vorbesc despre cele două cercuri. C. Titus Grigorovici
P.S. Am vorbit mai sus despre apucătura noastră ca profesori să le dăm prea multe detalii elevilor, cu informaţii colaterale, de obicei irelevante pentru blocul principal al lecţiei în sine. Legat de această apucătură, daţi-mi voie să vă dau aici un contraexemplu recent din propria activitate, mai exact de la adunarea fracţiilor ordinare. Încercând să le dau celor de-a 5-a nişte reguli clare, am fost tentat să scriu pe tablă că la adunarea sau scăderea fracţiilor ordinare acestea se aduc la numitor comun. Puteam să mă opresc aici, dar drăcuşorul matematicii m-a împins să continui: de obicei prin amplificare (dar merge şi prin simplificare). În ora respectivă, dar şi în ora următoare am putut apoi observa cum acel comentariu din paranteză doar îi bulversase pe cei mai instabili, care nu înţelegeau când trebuie să aplice amplificarea şi când simplificarea. Eu am inclus acea observaţie dintr-un puseu de ego profesoral, încercând să prezint lucrurile din start complet teoretic, deşi la nivelul exerciţiilor obişnuite cazurile de aducere la numitor comun prin simplificare sunt sub 1% din total. Încercând să repar situaţia în mintea celor mai slabi, mi-am jurat în suflet că mă voi abţine cât mai mult pe viitor de la aceste etalări de aspecte inutile aduse în faţa elevilor “mult prea devreme”.

