Unori Ministerul Educaţiei nu mai ştie ce să facă, aşa că oferă profesorilor ocazia să vină ei cu o propunere inovativă de programă. Ce înseamnă aceasta şi în ce direcţie trebuie o astfel de propunere să fie inovativă, asta nu este clar, deşi, poate era mai bine dacă ministerul împreună cu toate structurile sale de management a educaţiei dădeau nişte linii ghidante. Noi, oamenii de rând nu putem vrăji “la comandă” idei care să fie cu adevărat novatoare, dar totodată şi verificate în sensul eficienţei în condiţiile din ţara noastră. Pe de altă parte, nu se ştie nici odată “de unde sare iepurele”, adică de unde apare o idee bună. Am prezentat în eseul despre matematica naivă câteva idei despre acest nou concept de prezentare a cunoştinţelor matematice în funcţie de posibilităţile şi nevoile vârstelor elevilor, nu în funcţie de dorinţele foştilor diriguitori din Olimpul matematicii româneşti. Totuşi, conceptul este neclar şi prin faptul că îi lipsesc exemple de aplicare în viaţa de zi cu zi. Pentru aceasta voi încerca să prezint câteva situaţii din matematica gimnazială, acolo unde gradul de naivitate necesar este încă mai mare.
Să luăm un exemplu dublu pentru a clarifica lucrurile. Una din marile “minuni” cu care matematica gimnazială s-a catadicsit la reforma din 1980 a fost demonstraţia prin metoda reducerii la absurd. Aceasta era însă atât de inaccesibilă elevilor încât nu a reuşit să penetreze nici măcar fondul de probleme pentru olimpiade. Totuşi, era acceptată oficial şi păstrată în materie datorită celor două mari demonstraţii tradiţionale ce o foloseau: demonstrarea iraţionalităţii lui 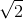 venită de la marele Euclid şi demonstrarea congruenţei unghiurilor alterne interne venită din axiomatizarea radicală a geometriei din jurul anului 1900 (amândouă erau în materia clasei a VI-a, dar capitolul despre rădăcina pătrată a fost mutat la sfârşitul anilor ‘90 în clasa a VII-a). Aceste demonstraţii nu se mai fac de mult cu elevii la clasă, dar abordarea şi ordonarea materiei în funcţie de ele este păstrată şi la ora actuală, fără ca lumea să fie conştientă de acest fapt. Să lămurim pe rând cele două situaţii.
venită de la marele Euclid şi demonstrarea congruenţei unghiurilor alterne interne venită din axiomatizarea radicală a geometriei din jurul anului 1900 (amândouă erau în materia clasei a VI-a, dar capitolul despre rădăcina pătrată a fost mutat la sfârşitul anilor ‘90 în clasa a VII-a). Aceste demonstraţii nu se mai fac de mult cu elevii la clasă, dar abordarea şi ordonarea materiei în funcţie de ele este păstrată şi la ora actuală, fără ca lumea să fie conştientă de acest fapt. Să lămurim pe rând cele două situaţii.
Ordonarea materiei în jurul temei TRIUNGHIUL era în anii ‘80 următoarea: triunghiuri şi construcţia lor; cazurile de congruenţă ale triunghiurilor; proprietăţile triunghiurilor isoscele; drepte paralele; axioma paralelelor şi unghiuri formate de două drepte paralele cu o secantă; suma unghiurilor în triunghi (citat din cuprinsul manualului de clasa a VI-a, autori Ion Cuculescu, Constantin Ottescu, din cele două exemplare ce le am pe-acasă, cel din 1979 şi cel din 1988). Punctul central al acestei secvenţe de lecţii era teorema de legătură între congruenţa unghiurilor alterne interne şi paralelismul dreptelor cu demonstrarea prin reducere la absurd, folosind congruenţa a două triunghiuri. De-abia după aceasta se putea demonstra şi suma unghiurilor în triunghi.
Ordonarea materiei la ora actuală este cam aceeaşi, în afara de demonstrarea ciudatei teoreme care nu se mai face la clasă de cca. 20 ani. Actualmente, legătura între dreptele paralele şi congruenţa unghiurilor alterne interne se face pe încredere, pentru că aşa zice profesorul. O a doua diferenţă faţă de anii ’80 este că depărtarea dintre prima lecţie despre triunghi şi momentul când se învaţă suma unghiurilor a crescut şi mai mult, între acestea parcurgându-se în prezent şi un capitol serios despre perpendicularitate.
Ce se întâmplă în aceste condiţii la clasă, depinde de la un caz la altul. Din multele variante în care elevii află despre acea sumă miraculoasă de 180o, doresc să evoc una, de care am aflat anul şcolar trecut. Profesorul de la clasă parcurge materia conform programei; aşa, măcar elevii nu ştiu despre ce-i vorba şi basta! Dar în piesa de teatru a acelei şcoli mai exista şi personajul numit profesorul de la opţional, care nu se simţea deloc dator a respecta programa colegului. Astfel, elevii află la opţional că suma unghiurilor ar fi de 180o, cu observaţia evidentă că profu’ de la clasă încă nu poate/nu vrea să v-o divulge. Eu nu doresc întoarcerea la vremurile de rigurozitate extremă din anii ’80-’90, dar nici o batjocură de felul acesta nu accept, la adresa gândirii logico-matematice pe care tocmai ne pregătim să le-o inducem elevilor.
O propunere inovativă simplă de aplicat de către orice profesor, pentru această parte de materie, ar fi studierea unghiurilor formate de două paralele cu o secantă înaintea lecţiei despre triunghi. Aceasta se poate face la fel ca în formatul actual, adică deducând intuitiv congruenţa unghiurilor corespondente, alterne interne etc. Eu, de pildă, folosesc aici o translaţie prin care justific congruenţa unghiurilor corespondente, iar apoi celelalte congruenţe se deduc uşor cu unghiuri opuse la vârf. Această mutare îmi permite includerea în prima lecţie despre triunghi a sumei unghiurilor, cu demonstraţie cu tot! Adică, din prima lecţie elevii învaţă definiţia, elementele, perimetrul şi suma unghiurilor în triunghi, având din start cea mai importantă proprietate a tringhiului. Nu mai insist cât de mult se simplifică lecţiile ulterioare despre triunghi, dacă avem de la început suma unghiurilor. Eu predau în acest format din anul şcolar 1994-1995 şi pot doar să privesc cu durere cum sunt chinuiţi majoritatea elevilor din celelalte şcoli, în formatul vechi. Ca o ultimă observaţie la acest subiect, trebuie precizat că ordinea din această propunere este similară cu ordinea existentă în manualele din anii ’70 ale profesorului A. Hollinger.
Abordarea temei despre RĂDĂCINA PĂTRATĂ se făcea în anii ‘80 în felul următor: rădăcina pătrată dintr-un număr natural pătrat perfect; rădăcina pătrată dintr-un număr raţional nenegativ; rădăcina pătrată cu aproximaţie de o unitate prin lipsă dintr-un număr raţional nenegativ; numere iraţionale; extragerea rădăcinii pătrate (citat din cuprinsul manualului de clasa a VI-a din 1979, autori C. P. Popovici, I. C. Ligor). Primele lecţii prezentau câteva elemente introductive greu de înţeles pentru elevul de rând, după care se trecea la demonstrarea iraţionalităţii lui 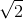 (demonstraţia arhi-cunoscută prin reducere la absurd), iar în final apărea şi algoritmul de extragere a rădăcinii pătrate. Exerciţiile rămâneau însă în zona aritmetică de extragere exactă sau aproximativă a rădăcinii pătrate. Urma un capitol despre mulţimi elementare de numere, în care se prezentau mulţimile de numere naturale, întregi, raţionale respectiv reale. Acolo găsim câteva întrebări în care copiii erau verificaţi dacă ştiu că
(demonstraţia arhi-cunoscută prin reducere la absurd), iar în final apărea şi algoritmul de extragere a rădăcinii pătrate. Exerciţiile rămâneau însă în zona aritmetică de extragere exactă sau aproximativă a rădăcinii pătrate. Urma un capitol despre mulţimi elementare de numere, în care se prezentau mulţimile de numere naturale, întregi, raţionale respectiv reale. Acolo găsim câteva întrebări în care copiii erau verificaţi dacă ştiu că 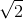 ş.a. nu sunt raţionale. Atât! Tot restul clasei a VI-a elevii rămâneau în zona aritmetică a rădăcinii pătrate pe care o exersau cu orice ocazie (mai urmau capitolele despre rapoarte şi proporţii, şi despre procente). De-abia în clasa a VII-a elevii treceau la calcule cu numere iraţionale, calcule ce reprezintă nivelul algebric al operaţiilor cu radicali.
ş.a. nu sunt raţionale. Atât! Tot restul clasei a VI-a elevii rămâneau în zona aritmetică a rădăcinii pătrate pe care o exersau cu orice ocazie (mai urmau capitolele despre rapoarte şi proporţii, şi despre procente). De-abia în clasa a VII-a elevii treceau la calcule cu numere iraţionale, calcule ce reprezintă nivelul algebric al operaţiilor cu radicali.
Odată cu mutarea capitolului despre rădăcina pătrată în clasa a VII-a, mutare efecuată la finalul anilor ’90, cele două părţi – cea aritmetică şi cea algebrică – au fost cumulate într-un capitol, partea aritmetică pierzându-şi mare parte din perioada sa de aplicaţie/dospire. Actualmente, elevii stau cca. o săptămână în starea aritmetică, după care se trece la calculul algebric cu numere iraţionale.
Oare, este bine aşa? Ce înţelege un elev, dacă scrie 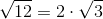 (forma algebrică) şi ce înţelege el din forma aritmetică
(forma algebrică) şi ce înţelege el din forma aritmetică 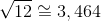 ? Forma aritmetică este una clară, practică, chiar dacă nu este super-exactă. Forma algebrică este exactă, dar de neînţeles pentru mintea umană normală. Elevul ar avea nevoie de o perioadă de acomodare cu noua operaţie, timp în care să calculeze rădăcina pătrată, în funcţie de natura sa (exactă sau aproximativă), după care, de-abia apoi să treacă la calcule algebrice cu numere iraţionale. În ţările din vestul Europei aşa se face.
? Forma aritmetică este una clară, practică, chiar dacă nu este super-exactă. Forma algebrică este exactă, dar de neînţeles pentru mintea umană normală. Elevul ar avea nevoie de o perioadă de acomodare cu noua operaţie, timp în care să calculeze rădăcina pătrată, în funcţie de natura sa (exactă sau aproximativă), după care, de-abia apoi să treacă la calcule algebrice cu numere iraţionale. În ţările din vestul Europei aşa se face.
Cât despre demonstraţia iraţionalităţii lui 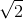 , unii profesori nu o mai prezintă (adică merg pe încredere), pe când alţii o fac la clasă, dar elevii în general nu o înţeleg. Părerea mea personală estă că aceasta reprezintă un item clar pentru materia de clasa a IX-a.
, unii profesori nu o mai prezintă (adică merg pe încredere), pe când alţii o fac la clasă, dar elevii în general nu o înţeleg. Părerea mea personală estă că aceasta reprezintă un item clar pentru materia de clasa a IX-a.
O propunere inovativă simplă de aplicat de către orice profesor, pentru această parte de materie, ar fi împărţirea temei în două părţi distincte. De pildă se poate rămâne în starea aritmetică în semestrul I din clasa a VII-a, iar apoi se trece în semestrul II la calculele în forma algebrică cu numere iraţionale. Desigur că s-ar putea reveni tot aşa de bine şi la forma veche, cu partea aritmetică în clasa a VI-a, iar partea de tratare algebrică de-abia în clasa a VII-a.
Un aspect aparte al acestui subiect îl reprezintă forma de aplicare a rădăcinii pătrate în cadrul calculului cu teorema lui Pitagora, în cazul rezultatelor ne-exacte. Calculele de lungimi, perimetre şi arii reprezintă partea practică a geometriei plane, iar la acestea sunt mult mai clare calculele aproximative ale rădăcinii pătrate (adică forma aritmetică). Prin acestea elevul îşi poate dezvolta o percepie naturală şi un bun-simţ al calculului (de exemplu, cam cât este de lungă diagonala unui pătrat cu latura de un metru, dar şi multe alte exemple “practice”). Trecând abia ulterior şi la calcule cu exprimarea rezultatelor în formă exactă iraţională, le permite elevilor realizarea unei înţelegeri naturale a matematicii şi a conexiunilor dintre elementele acesteia.
De pildă, eu încep materia clasei a VII-a cu un mega-capitol compus din trei părţi distincte: 1) Rădăcina pătrată şi extragerea acesteia, cu rezultate naturale, respectiv cu rezultate aproximative; 2) Aria şi formulele de calcul pentru figurile de bază (triunghiuri şi patrulatere); 3) Teorema lui Pitagora (demonstrată prin arii) cu calcule pe două nivele: la început cu rezultate exacte, pe baza tripletelor pitagorice, iar apoi cu rezultate ne-exacte, calculate aproximativ. Aici ajungem să exersăm cu sens extragerea aproximativă a rădăcinii pătrate. De-abia în semestrul II introduc noţiunea de număr iraţional, prezint scoaterea de sub radical, facem primele calcule algebrice cu numere iraţionale şi reluăm probleme cu calcul de arii şi perimetre prin teorema lui Pitagora, dar unde dăm rezultate iraţionale exacte.
Consider că aceste propuneri ar fi parte activă a unei forme de matematică naivă potrivită, adaptată vârstei gimnaziale, prin care elevii să urce liniştit, treptat către nivelele intelectuale necesare promovării cu succes a examenului de Evaluare Naţională de la sfârşitul clasei a VIII-a.
18 iulie 2016
Prof.C. Titus Grigorovici
Vezi și: Matematica naivă

Ce frumos predati!!!Cred că elevilor le face plăcere să va aibe ca profesor.