Dacă ajungi într-o capitală mondială ca turist – de pildă Roma – ai foarte multe de vizitat. Fie că ajungi la Roma pentru două zile, fie că ajungi pentru o săptămână, oricum ai aceeaşi problemă: să stabileşti care sunt cele mai importante locuri de vizitat în sejurul tău. Pentru alegerea respectivă apelezi la un ghid: sau mergi cu un grup organizat cu un ghid, sau cumperi un ghid scris, sau te îndrumă o cunoştinţă. De la acesta îţi doreşti să fi îndrumat în ordinea importanţei şi vei fi supărat dacă ai fi fost plimbat de pildă la nenumărate biserici, dar nu ai văzut Columna lui Traian.
Capitolul despre Cerc se aseamănă foarte mult cu un astfel de oraş: sunt foarte multe de văzut, iar elevii trebuie îndrumaţi în funcţie de timpul alocat şi de nivelul clasei, astfel încât să vadă ce este mai important în condiţiile date. Din păcate şi aici programa gafează profund chinuind copiii cu o lecţie fără sens, rămasă acolo din vremuri de demult, ca parte dintr-o construcţie de rigurozitate universitară ciudată. Să analizăm situaţia.
Capitolul începe cu lecţia introductivă despre definiţie, rază, diametru, coardă, arc, semicerc etc. Lecţia a doua face legătura între măsura de unghiurilor la centru şi măsura arcelor de cerc. Să analizăm lecţia a treia: Coarde şi arce în cerc; diametru perpendicular pe o coardă; arce cuprinse între coarde paralele; coarde egal depărtate de centru (lecţie pe care unii profesori o şi întind pe două ore. Pentru ce este bună această lecţie? La ce îi folosesc aceste teoreme elevului? Analizând “utilitatea” lor, ajungem la concluzia că acestea reprezintă trei sferturi dintr-un drum ce ar trebui să demonstreze că tangenta la cerc este perpendiculară pe raza dusă în punctul de contact. Această ultimă teoremă însă nu se demonstrează, aşa că teoremele din lecţia a treia nu îşi au nici un rost. Elevii sunt chinuiţi gratuit cu nişte teoreme fără sens! Singurul aspect ce se opţine clar este înverşunarea şi scârbirea şi mai profundă a elevilor împotriva geometriei.
Dacă ne întoarcem la ideea de matematică naivă, teoremele din lecţia a treia nu au pentru elevi niciun rost. În primul rând, că demonstrează adevăruri intuitiv evidente. Apoi, informaţiile respective nu se folosesc în nici o problemă: profesorii au dificultăţi în a găsi aplicaţii la aceste teoreme! Singurul raţionament ce se foloseşte de aici este faptul că triunghiul determinat de două raze şi o coardă este isoscel. Dar pentru asta oricum nu ai nevoie de vreo teoremă specială.
Aici se ridică o mare întrebare: pentru ce parcurgem anumiţi itemi? De pildă, de ce parcurgem o anumită teoremă? În principiu, pentru elevi această întrebare are două-trei răspunsuri: fie pentru utilitatea sa (ca aplicaţii în probleme sau în susţinerea unei alte teoreme importante), fie pentru demonstraţia sa deosebită. Dacă o teoremă este foarte importantă prin prisma aplicaţiilor, dar are o demonstraţie foarte grea, atunci teorema poate fi dată naiv, pe încredere, adică fără demonstraţie, elevii bucurându-se în schimb de aplicaţii uşoare. Este cazul teoremei tangenta la cerc este perpendiculară pe raza dusă în punctul de contact, care permite aplicaţii uşoare cu teorema lui Pitagora, dar şi parcurgerea în continuare a teoremei “ciocului de cioară” despre cele două tangente de la un punct la un cerc. Teorema despre măsura unghiului înscris în cerc are şi o demonstraţie frumoasă, dar şi aplicaţii interesante.
Nu-i clar ce înţelege onor Ministerul prin propuneri inovative de programă, dar eu consider că astfel de criterii ar trebui să stea la baza alegerii lecţiilor şi a itemilor de parcurs. De exemplu, eu din prima lecţie de la cerc concluzionez că două raze împreună cu coarda determinată de acestea formează un triunghi isoscel, după care elevii şi primesc aplicaţii de calcul cu teorema lui Pitagora în triunghiul isoscel respectiv. În lecţia a doua parcurg Cercul lui Thales (două coarde cu un capăt comun iar celelalte două capete diametral opuse sunt perpendiculare), demonstată cu triunghiuri isoscele, şi teorema cu tangenta la cerc este perpendiculară pe raza dusă în punctul de contact, fără demonstraţie. Din acest moment am multe aplicaţii, elevii găsind un sens în lecţiile acestui capitol. Iată şi un exemplu de aplicaţie în sensul construcţiilor cu rigla şi compasul: folosind Cercul lui Thales se pot trasa înălţimile într-un triunghi dat, doar cu rigla şi compasul.
În ultimii ani am încheiat acest capitol cu două teoreme duale, în pereche, ce nu le parcurg pentru vreo aplicaţie a lor, ci doar pentru frumuseţea demonstraţiei. Fiecare demonstraţie în sine nu este deosebită. Privite însă împreună, cele două teoreme cu demonstraţii corespunzătoare trezesc în rezolvitor acea stare mult dorită de uimire, caracterizată simplu printr-un mare “UAU!”. Este vorba despre proprietatea unghiurilor patrulaterelor înscrise în cerc (inscriptibile), respectiv proprietatea dual-omoloagă a laturilor patrulaterelor circumscrise unui cerc (circumscriptibile). În imaginea de mai jos puteţi vedea blocul principal al acestei lecţii
Numărul π nu apare în capitolul despre cerc, ci într-un capitol artificial, imediat după cerc. De ce îl cataloghez drept artificial? Pentru că acest capitol dă mai multă atenţie celor trei poligoane regulate importante decât drumului către numărul π. Oricum, drumul respectiv nu este parcurs în lecţii, chiar existând profesori care “o lălăie” într-atăt încât nici nu mai ajung la numărul π în clasa a VII-a.
Pentru început, în acest proces noi măsurăm circumferinţa diferitor obiecte circulare şi calculăm raportul faţă de diametrul cercului, obţinând diferite valori între 3 şi 3,2 (la diferite oale este cel mai folositor un metru de croitorie). Ca exemplu mai special, în curtea şcolii noastre avem un teren circular de beton; vă puteţi închipui ce distracţie a fost în ultimii ani în cadrul Săptămânii Şcoala Altfel, când am măsurat cu o sfoară şi cu mulţi elevi circumferinţa terenului.
La un nivel intelecual mai înalt, după ultima problemă de la Examenul de Evaluare Naţională din iunie 2016, eu oricum m-am hotărât să parcurg şi octogonul regulat (cu unghiul la centru de 45o la fiecare felie-triunghi isoscel) cât şi dodecagonul regulat (cu unghiul la centru de 30o), studiind perimetrul şi aria, şi procesul în care acestea se apropie de valorile cercului. Apropos, verificaţi cât de uşor se poate arăta că aria dodecagonului regulat înscris în cercul de rază r este exact 3r2, folosind pentru calcularea ariei fiecărei felii 1/12 doar teorema despre cateta opusă unghiului de 30o. Pentru calcularea perimetrului poligonului regulat cu 12 laturi trebuie însă muncit însă ceva mai mult. Lucrând cu aproximări de trei zecimale, se obţine în final raportul perimetru/diametru de 3,10 (doar pentru elevii de 10).
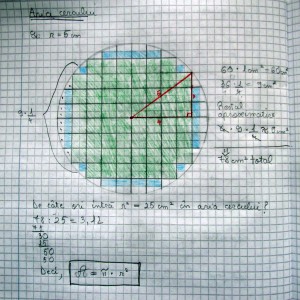
O apropiere mai bună de valoarea lui π am obţinut, mult mai uşor şi pe mintea tuturor, printr-o altă abordare de tip Laboratorul de matematică. Astfel, elevii au desenat pe caietul de matematică, cu pătrăţele de 0,52 = 0,25cm2, un cerc cu raza de 5cm (prin triunghiul egiptean, avem garanţia unei exactităţi deosebite în câteva puncte de pe cerc). Elevii au trebuit să determine pur şi simplu aria discului prin aproximaţie, numărând cm2, jumătăţile şi sferturile, cât şi aproximări ale resturilor pătrăţelelor rămase. Rezultatul de 78 : 25 = 3,12 pentru raportul dintre aria cercului şi aria pătratului pe rază este unul foarte bun şi orice elev îl înţelege. Vedeţi această parte de lecţie cu matematică naivă în următoarea imagine. Trecerea de la aceste rezultate (atât la perimetrul cercului cât şi la aria discului) la cunoscutul 3,14 se face pe încredere şi toţi elevii sunt bucuroşi că au înţeles despre ce este vorba.
1 august 2016
Prof. Titus Grigorovici


Astfel de lucruri as fi dorit să învăț si eu la metodica predării matematicii.Unde as putea să urmăresc mai multe lecții ale dumneavoastră ,deoarece cred ca as avea multe lucruri de învățat și mi-ar face mare plăcere.Multumesc.