În postarea Ordinea operaţiilor în clasele primare din februarie 2016 am discutat despre cum este înţeleasă sau nu ordinea operaţiilor în ciclul primar. Problemele mari sunt legate de ordinea efectuării între operaţia de adunare şi cea de scădere, şi se pare că problemele sunt de fapt la nivelul unor învăţătoare, care apoi îi învaţă greşit pe copii. În acest sens, când simt că „miroase” în clasă a o astfel de greşeală, eu îi întreb pe elevi: între adunare şi scădere, care operaţie se face prima?. Vă daţi seama ce distractiv-bulversantă devine ora dacă primesc un răspuns de tipul: adunarea!, la care dau din cap că-i greşit; apoi, repede careva are impulsul de a da celălalt răspuns posibil, după mintea lor: scăderea!, la care eu iarăşi răspund că NU!. După o clipă de linişte bulversată, careva răspunde sigur pe el: prima care-i scrisă!, iar eu în sfârşit mă arăt mulţumit. Uneori mai pun şi a doua întrebare: între înmulţire şi împărţire, care operaţie se face prima?, iar elevii ştiu de data asta răspunsul corect din prima.
La adresa Ordinea operaţiilor pe internet (august 2016) am tratat exemplul unei situaţii de ordinea operaţiilor propuse “internauţilor” străini, care scotea în evidenţă faptul că unele astfel de exerciţii nu se pot rezolva cu “calculatorul de buzunar”, fie el chiar şi din “deşteptofon” sau de pe laptop. În momentul acela mândria noastră de mari olimpici ne făcea să pufnim de râs profund dispreţuitor.
Iată, însă, cum arată o astfel de situaţie pe plaiurile mioritice ale internetului. Este vorba de banala “problemă” 7 – 5 + 2 = ?, despre care puteţi lectura prezentarea de la adresa Problema ASTA a impartit Romania in doua!. Dacă nu doriţi, iată aici materialul respectiv în variantă prescurtată (corectat şi cu diacritice).
*
Sunt de-a dreptul şocat. O problemă de clasa pregatitoare a reuşit să divizeze poporul român consumator de internet. Studiu de caz pentru ce se întâmplă acum în România. Se dă problema:

Şi mi-am zis că e o glumă proastă. Că nimeni nu va comenta la prostia asta şi că toată lumea ştie rezultatul. Greşit! E momentul în care îmi dau seama că trăiesc într-o mare bulă şi că realitatea doare. 52 de oameni au apreciat părerea lui Andrei. 52 DE OAMENI! Nu numai că Andrei şi Matematica sunt paraleli, dar oamenii au aprecit şi faptul că el îi face idioţi pe toţi ceilalţi. Cum nu se poate mai bine! Apoi vine rândul „idioţilor”:
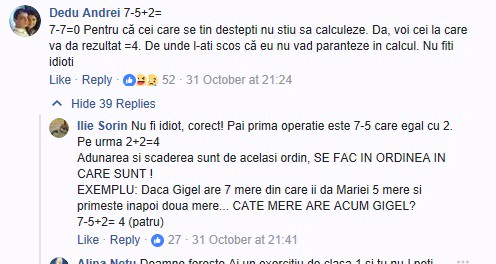
De aici, cele două tabere, „idioţii care cred că e 0” şi „idioţii care cred că rezultatul e 4”, încep să se certe şi să îşi arunce jigniri despre mamele şi rudele celorlalţi, (…), despre „scoala care au facuto”. Te doare mintea! 86 de oameni au apreciat explicaţia lui Mihai, dar şi faptul ca el i-a numit „cretini”:
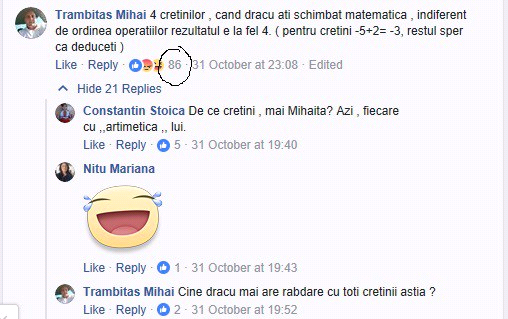
Iată concluziile lui Silviu Iliuţă, autorul acestui eseu publicat pe Cronici pe bune:
- O problemă simplă a reuşit să creeze pe net două tabere care se jignesc, se acuză, aruncă cu rahat. incredibil! Vă daţi seama ce se întamplă la problemele adevărate şi cât de uşor e să divizezi românii, aruncându-le o simplă prostie pe net?
- Cu riscul de a părea extremist sau orice „-ist”, eu cred că cei din tabăra celor cu răspunsul 0 nu ar trebui să voteze. Trebuie să li se explice frumos care e treaba cu ordinea operaţiilor. Dacă insistă în răspunsul lor, cred că nu ar trebui să meargă la vot (…) Pentru că nu ai cum să votezi, dacă Olguţa îţi promite că îţi creşte salariul cu 0 lei, iar tu te bucuri şi îi dai votul. Nu ai cum să ai drept de vot, dacă Liviuţ îţi spune că ţi se înmulţesc veniturile cu 1, iar tu îi dai votul pentru asta.(…) Pur şi simplu ţi-e mai bine dacă votează alţii pentru tine! Eşti mult mai în siguranţă. (…)
- Oricât de prost pregătit e un om, nu trebuie să îl jigneşti! Nu eşti DELOC mai presus decât el dacă îl faci „idiot”! Încearcă să îi explici frumos, chiar dacă el este agresiv. Este foarte important să avem înţelegere. (…)
- Daca aţi citit acest articol şi încă vă întrebaţi care e răspunsul corect, vă rog frumos, în genunchi, să nu mergeţi la vot! Din spirit civic. Nu este nicio problemă că nu ştiţi, ar fi de apreciat dacă aveţi deschidere să învăţaţi, dar chiar este o problemă dacă votaţi.
*
Da, să revenim la partea de matematică, oricât de minimalistă ar fi aceasta în subiectul de faţă. Oricum, putem sta liniştiţi: în meciul „celor cu 4” în confruntare cu „cei cu 0”, scorul final pare să fie undeva la 86-52, raportul fiind cam de 3 la 2. Lăsând gluma de-o parte, ar trebui să vedem de unde vine o astfel de minunăţie; de ce totuşi „doi din cinci români” cred în a doua variantă? La începutul prezentului articol am amintit bănuiala că unele învăţătoare traduc simpla enumerare a operaţiilor de ordinul I într-o ordine obligatorie. De pildă, în citatul: Într-un exerciţiu în care apar operaţii de adunare, scădere şi înmuţire se rezolvă întâi înmulţirea, apoi adunarea şi scăderea (Matematică şi explorarea mediului, manual pentru clasa a II-a, Didactica Publishing House), diferite persoane cu o structurare mai filologică a creierului vor înţelege regula astfel: Într-un exerciţiu în care apar operaţii de adunare, scădere şi înmuţire se rezolvă întâi înmulţirea, apoi adunarea şi doar apoi scăderea.
Nu vreau să discut despre cine este responsabil pentru această greşeală din mintea acestor doamne învăţătoare; mai mult mă interesează despre cine este în măsură să corecteze respectivul aspect. În acest sens cred că noi, profesorii de matematică ar trebui să ne propunem să abordăm cu tact şi cu respect faţă de colegele noastre acest subiect şi să încercăm să eradicăm defectul din gândirea lor în discuţii calme şi civilizate cu dânsele. Nu e simplu, dar cred că se poate.
Putem privi lucrurile şi altfel: se prea poate ca învăţătoarea să fi predat bine, dar această confuzie să apară în mintea micuţului, neatent, neconcentrat, nepasionat de fenomenul matematic, poate şi alţi de ne-…, în mintea sa rămânând peste ani doar vocea stridentă a doamnei învăţătoare care striga la el: CARE-I ORDINEA OPERAŢIILOR? CE OPERAŢIE TREBUIE FĂCUTĂ AICI PRIMA, COPILE?, astfel încât atunci când a văzut ca adult scrierea 7 – 5 + 2 să se fi declanşat doar amintirile spaimelor din copilărie, gândind cu o voce interioară tremurândă: Oare aici pe care trebuia să o fac prima? Probabil că adunarea, că ştiu eu că în copilărie tot urla aia la mine dacă le făceam în ordinea în care erau scrise. Astfel, cred că este foarte posibil că şi aspectele psihologice să influenţeze situaţia acestui 7 – 5 + 2, cel puţin în unele cazuri.
Evident că persoanele care susţin că se face adunarea înaintea scăderii nu şi-au însuşit cum trebuie principiul conform căruia semnele de + şi – dintre numere pot fi privite atât ca semne de operaţie, cât şi ca semne ale unor numere pozitive sau negative. Aici trebuie atrasă atenţia şi asupra unei alte situaţii care este cu totul nouă pentru noi. În scrierea 7 – 5, al cui este semnul minus? Deci, cum se citeşte o scădere? Se citeşte 7 – … 5 sau se citeşte 7 … – 5? (cele trei punctuleţe mimează o pauză) Obişnuinţa la baza învăţământului românesc, încă de la începuturi este că minusul aparţine lui 7. De unde ştiu asta? Păi uitaţi-vă unde pune învăţătoarea semnul de scădere la o scădere cu numerele unul deasupra celuilalt: după numărul descăzut, în dreapta sa. Acolo îl punem şi noi profesorii! Forma corectă ştiinţific este însă că minusul este al lui 5. Aşadar semnul de scădere ar trebui pus lângă scăzător, la stânga sa, adică în faţa sa. De ce să-l punem acolo?, veţi întreba. Pentru că aşa e corect, iar asta ar preîntâmpina multe neînţelegeri. Nu mă credeţi, aşa că scot „artileria grea” a argumentelor: aşa fac şi nemţii, dar şi alţi vestici! Uitaţi în următoarea poză:
 Aţi văzut unde este poziţionat semnul de scădere, sau v-aţi uitat doar la mitraliera învăţătoarei? Amândouă se potrivesc în oarecare măsură discuţiei noastre. Revenind la semnul minus din scădere, acesta poate fi pus şi la scăderile din cadrul împărţirii. Nu înţelegeţi cum? Ia aduceţi-vă aminte cum se face chestia asta în algoritmul de împărţire a polinoamelor: este acelaşi lucru, doar că nemţii o fac de la început în forma corectă. De ce? Că-s nemţi şi aşa fac ei lucrurile, corect din prima. De ce nu le facem şi noi aşa? Cred că intuiţi răspunsul.
Aţi văzut unde este poziţionat semnul de scădere, sau v-aţi uitat doar la mitraliera învăţătoarei? Amândouă se potrivesc în oarecare măsură discuţiei noastre. Revenind la semnul minus din scădere, acesta poate fi pus şi la scăderile din cadrul împărţirii. Nu înţelegeţi cum? Ia aduceţi-vă aminte cum se face chestia asta în algoritmul de împărţire a polinoamelor: este acelaşi lucru, doar că nemţii o fac de la început în forma corectă. De ce? Că-s nemţi şi aşa fac ei lucrurile, corect din prima. De ce nu le facem şi noi aşa? Cred că intuiţi răspunsul.
Revenind la dificila noastră problemă cu ordinea operaţiilor, cred că am fost un pic cam necinstit la începutul acestei postări, în sensul că nu cred că doar învăţătoarele sunt de vină. Mai exact, dacă noi suntem atât de buni pe lângă dânsele, de ce nu remediem noi problema? Din clasa a 5-a toţi elevii ajung pe mâna unui profesor de matematică şi totuşi 2 din 5 internauţi au dat-o în bară cu banala secvenţă 7 – 5 + 2. Oare de ce? Cum se poate întâmpla aşa ceva? Păi, să vă prezint bănuiala mea: cu o programă atât de încărcată şi cu atâta preocupare pentru olimpiade încă din clasa a 5-a, cine mai are timp să se ocupe de ordinea operaţiilor din capul „elevilor slabi”? Pentru că da, profesorul de matematică visează numai la chestiile grele. Să corectezi astfel de gafe din gândirea elevilor trebuie să te ocupi măcar o oră, poate chiar două, cu astfel de banalităţi, iar apoi, ulterior să mai reiei subiectul de câteva ori ca să-l fixezi definitiv. Pentru asta trebuie să faci tu personal multe fişe, pentru că în culegeri nimeni nu pune „exerciţii pentru proşti”; toţi vrem să ajungem cât mai repede în zona „de excelenţă”. E greu, ştiu, să te cobori la nivelul „celor slabi” şi să te preocupi şi cu ei, dar dacă noi n-o facem, n-o va face nimeni. Ştiu, veţi răspunde că nu e vina noastră, a profesorilor de la clasă; s-o remedieze familia, direct sau prin intermediul meditatorul particular! Ce mă interesează pe mine chestia asta? Înspectorul de mate îmi cere şi mă laudă pentru rezultate la olimpiadă, nu pentru „looseri” recuperaţi. Un profesor bun se adresează în lecţii elevilor buni, nu codaşilor clasei.
Exagerez? Poate. Pentru o impresie artistică mai bună am dat un pic drumul unui ton mai agresiv, dar realitatea nu este deloc departe de prezentarea mea. Haideţi să dau câteva exemple culese de curând (adică în luna martie 2018), care ne arată cum materia este îngreunată artificial de către profesori şi dusă uneori departe de orice posibilitate de înţelegere de către elevi, potrivită vârstei şi cunoştinţelor acestora. Materia „zboară peste elevi” atât de sus încât de multe ori rezultatul mult lăudatului învăţământ românesc este cel văzut în exemplul de mai sus cu 7 – 5 + 2.
Trigonometria în clasa a 7-a se face în triunghiul dreptunghic, aplicându-se unghiurilor ascuţite din acesta. În clasa a 7-a nu se învaţă funcţii trigonometrice, pur şi simplu pentru că elevii încă nu au învăţat noţiunea de funcţie. În clasa a 7-a profesorul trebuie să aleagă titlul lecţiei undeva între Trigonometrie, Elemente introductive de trigonometrie sau poate Rapoartele trigonometrice. În clasa a 7-a sinus nu este funcţie ci este raportul dintre cateta opusă unui unghi ascuţit şi ipotenuză. Şi dacă tot am ajuns la unghiurile ascuţite pentru care calculăm rapoartele respective, aceste unghiuri particulare sunt 30o, 45o şi 60o. În nici un caz nu le putem da elevilor un tabel extins cu valorile 0o şi 90o, pentru că elevii nu-şi pot imagina cum este acela un triunghi dreptunghic cu un unghi de 0o sau cu încă un unghi de 90o. La fel de absurd ar fi dacă elevul s-ar poziţiona în unghiul drept încercând apoi să caute cateta opusă.
Acestea sunt gafele de predare cu care mă întâlnesc din când în când. Acum însă mi-a fost sesizat cazul unui coleg care a tratat aproape o oră întreagă funcţile trigonometrice fără să vorbească despre triunghiul dreptunghic, deci nici despre laturile sale. În schimb, pe lângă diferitele „formule fundamentale”, aflăm că dacă unghiul x este obtuz atunci cos x < 0 (!!!). Urmează multe exerciţii în care pornind de la o valoare a unei funcţii trigonometrice se calculează celelalte trei. Apoi, de niciunde apare brusc sin30o = ½ din care sunt deduse în continuare celelalte – da, aţi ghicit – pe baza formulelor fundamentale. Abia acum, spre sfârşitul orei, apare un nou titlu: Triunghiul dreptunghic Funcţii trigonometrice în care vedem în sfârşit un triunghi dreptunghic şi găsim rapoartele cunoscute sin = cateta opusă/ipotenuză etc. Aici elevii sunt informaţi că dacă cunoaştem un unghi (30o, 45o sau 60o) şi o latură, aplicăm funcţiile trigonometrice şi aflăm TOT. În sfârşit ajungem la primul exemplu folositor elevului de clasa a 7-a, dar după prima latură calculată s-a sunat, deci s-a dat tema şi gata ora. (din nou: !!!)
Descompunerea în factori a expresiilor de tipul x2 + bx + c în clasa a 7-a este un titlu destul de general şi se face mai mult pe cazul formulelor de pătrat a binomului. De abia în semestrul I al clasei a 8-a se cere mai serios să descompună toată lumea expresii de tipul x2 + 3x – 10 etc. Ecuaţia de gradul II vine în clasa a 8-a semestrul II, deşi la examen nu s-a dat în ultimii ani deloc. Elevii încep de abia în clasa a 9-a să se întâlnească puternic cu formulele generale ax2 + bx + c = 0, Δ = b2 – 4ac şi x1,2 = –b ± radical Δ supra 2a (scuze de scriere, ca să nu aveţi probleme la citire) şi respectiv ax2 + bx + c = a(x – x1)(x – x2). A da elevilor în clasa a 7-a forma generală a rezolvării ecuaţiei de gradul II pentru a avea o formă generală de descompunere, înaintea oricărei variante particulare, este pur şi simplu bătaie de joc la adresa gândirii elevilor. Iată doar un argument în acest sens: elevii tocmai ce au învăţat formulele binomiale în care literele reprezintă numere doar în valoarea lor absolută, nu şi cu semnul lor. Astfel, de exemplu în cazul (x – 3 )2, unde a = x şi b = 3, aplicăm formula pătratul unei diferenţe. Atenţionez că în mintea elevilor din aceast moment b nu este – 3, aşa că nu aplicăm formula pătratul unei sume, după modelul [x + (– 3)]2 (acest pas, includerea semnului în literă, acesta apare doar la formula pătratul unui trinom; la aceasta nu se mai dau toate variantele de formule, în toate combinaţiile de semne + sau –, elevul fiind forţat aici să vadă numărul împreună cu semnul său). Ca urmare, în calculele de la formulele generale pentru ecuaţia de gradul II elevii vor greşi masiv la semne. Sigur, putem striga la ei, îi putem ameninţa cu lucrare de control, dar cu ce preţ, mai ales că oricum ei încă nu au văzut nici măcar o singură ecuaţie particulară de gradul II. Las cititorului „bucuria” de a găsi şi alte contra-argumente. Precizez doar că acest exemplu apare destul de des în ultima vreme, tot mai mulţi profesori preferând să „scurtcircuiteze” drumul greu de formare a gândirii algebrice a elevilor de clasa a VII-a, dându-le o reţetă general valabilă cu care să-i terorizeze. Şi asta în condiţiile în care mare parte din elevii claselor nu stăpânesc formele elementare de descompunere în factori.
Desigur că acestea nu sunt exemple izolate. Ce părere aveţi de un profesor de liceu care-i explică unui elev de clasa a VIII-a rezolvări prin radiani? Iar copilul docil stă să treacă urgia peste el, încercând să înţeleagă cumva chestia asta prin regula de trei simplă. Sunt de acord că-i va folosi pe viitor, dar atunci hai să punem învăţătoarele să facă radicali cu ei, iar în clasa a V-a, imediat după operaţia de putere am putea face şi logaritmii, că „ce-are?”, le va folosi mai târziu.
Să mă opresc? Veţi spune că exagerez, aşa că haideţi să mai dăm două exemple, ca să ne convingem de magnitudinea fenomenului. Ce spuneţi de titlurile următoare la clasa a VII-a (acum, în aprilie) şi, mai ales, ce părere aveţi despre efectul acestor lecţii într-o clasă de nivel mediu fără participanţi la olimpiada judeţeană? Iată: Valoarea minimă şi valoarea maximă a unui polinom de gradul II; sau, lecţia următoare: Ecuaţii de gradul II cu mai multe necunoscute, în condiţiile în care elevii clasei respective încă nu reuşesc clar să facă ecuaţii particulare sau generale de gradul II cu o necunoscută (toate acestea la titlul oficial Ecuaţii de forma x2 = a). Ar trebui să mulţumesc colegului respectiv pentru aceste exemple (vreau să spun: contra-exemple), dar sunt doar scârbit de situaţia respectivă.
Oare cum se simte un profesor care face aşa ceva elevilor, fără nici un dram de empatie faţă de fiinţa şi gândirea elevului, a elevului disperat că nu pricepe nimic sau mai nimic? Sunt sigur că mulţi elevi sunt leneşi şi nu au nici un chef să înveţe. Sunt sigur că mulţi nu au dotarea necesară pentru a înţelege matematica în general. Dar tot aşa de sigur sunt că mulţi dintre adulţii avariaţi matematic reprezintă victime rămase în urma activităţii unor învăţătoare incompetente sau a unor profesori exagerat de ambiţioşi (frustraţi?), care fac lecţii mult prea grele şi mult prea devreme, fiind total lipsiţi de orice urmă de tact pedagogic. Cu astfel de contraexemple de lecţii ale unor colegi, îmi vine greu să mă semnez ca profesor. CTG
