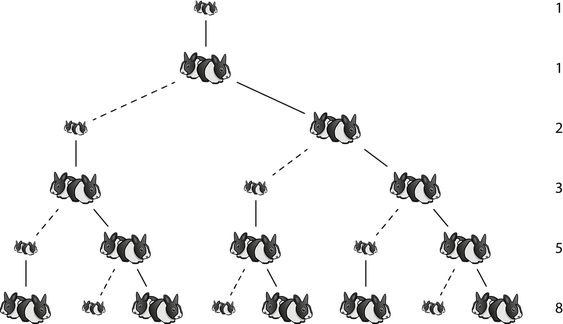
În postarea precedentă am deschis sacul din care au ieşit iepuraşii lui Fibonacci, aducând cu ei – ca dintr-un joben magic – numerele din renumitul şir. Dacă tot am deschis subiectul, merită să mai zăbovim puţin în jurul acestor numere renumite.
În primul rând trebuie subliniat faptul că problema respectivă este profund falsă din punct de vedere al realităţii speciei şi a felului în care se înmulţesc iepuraşii. La fel ca majoritatea problemelor de matematică, şi aceasta descrie şi se bazează pe o situaţie idealizată, profund diferită de realitatea înconjurătoare. Cu atât mai şocantă este această constatare cu cât există multiple exemple de situaţii profund naturale în care numerele izvorâte din problema iepuraşilor apar totuşi în realitatea înconjurătoare în mod nemijlocit şi fără de tăgadă. Sunt renumite diferitele situaţii din lumea vie în care se găsesc urme ale numerelor lui Fibonacci, spirala logaritmică sau secţiunea de aur fiind prezente “te miri unde”.
Există foarte multe exemple, dar nu mi-am propus aici o prezentare exhaustivă, nici măcar o enumerare a celor mai cunoscute astfel de situaţii unde sunt întâlnite renumitele numere 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … . Le puteţi găsi în bogata literatură tipărită sau pe internet (de pildă Mario Livio, Secţiunea de aur, Humanitas). Doar un singur exemplu doresc să vă prezint în această postare, anume unde şi cum am găsit eu numere Fibonacci pe un fruct de ananas.
Analizând un astfel de fruct, observăm că suprafaţa sa este formată din nişte “celule” oarecum patrulatere destul de ordonat aliniate. De fapt acestea sunt seminţe iar alinierea lor poate fi privită ca o înşiruire de dale pentru un posibil “şotron”.
Mai exact spus, fiecare astfel de poziţie este parte a două alinieri, una care urcă spre stânga şi una care urcă spre dreapta. Analizând cu atenţie sporită vedem că alinierea care urcă înspre stânga este mai lină, pe când alinierea care urcă spre dreapta este mai abruptă.
Interesant este că cele două alinieri care pornesc dintr-o poziţie, cea înspre stânga şi cea înspre dreapta, ajung să se reîntâlnească în partea cealaltă a ananasului. De fapt nu se întâlnesc exact în partea opusă, şi asta datorită diferenţei de înclinaţie. Astfel, de la un punct comun, să-i zicem A punctului de jos, până la celălalt punct comun B al celor două alinieri oblice, situat mai sus, drumurile pe cele două trasee diferă ca lungime: drumul care urcă lin spre stânga este mai lung, pe când drumul care urcă abrupt spre dreapta este clar mai scurt.
Surpriza apare atunci când numărăm paşii ce trebuie făcuţi pe cele două drumuri: de la A la B pe drumul abrupt dar mai scurt avem de făcut 8 paşi, pe când pe drumul lin dar mai abrupt sunt de făcut 13 paşi! UAU!!! DA!!! Exact 8, respectiv 13 paşi. La alte specii pot fi găsite alte numere Fibonacci alăturate. De pildă la o creangă de pin am găsit numerele Fibonacci consecutive 5 şi 8 (cu cât avansăm, raportul a două numere alăturate din acest şir aproximează tot mai bine renumitul număr “fi” φ ≈ 1,618).
Păi, ştiu ananaşii sau pinii matematică? Multe persoane au în momentul acesta o trăire de uluială profundă, ceva de genul: plantele sunt creaţia lui Dumnezeu; asta este o urmă clară şi de netăgăduit lăsată de Dumnezeu de când a creat lumea. Problema cu iepuraşii era clar artificială, dar această situaţie este una profund naturală şi realistă. Încă o dată: UAU!!!
De obicei, prima întrebare ce îmi este adresată în acest moment este dacă toţi ananaşii au chestia asta. Cel mai bine ar fi să mergeţi şi să verificaţi în supermarket (este distractivă imaginea a doi elevi distrându-se într-un magazin la cutia cu ananaşi, numărând bunbii respectivi, când un angajat vine şi îi ia la rost, că “ce fac acolo?”, iar aceştia să răspundă “ne facem tema la mate, ne-a dat profu’ să numărăm pătrăţelele de pe ananas!”).
Răspunsul la întrebarea dacă întotdeauna se întămplă aşa, este în principiu afirmativ, doar că aceste fructe nu sunt obligatoriu perfecte, ci au dereglări ale rândurilor în anumite părţi. De pildă, exemplarul din aceste poze dovedeşte o dereglare a rândurilor pe partea surprinsă în prima poză. Concret, pentru a fi sigur că pot face pozele pentru prezentul articol, pe acest fruct l-am verificat cu atenţie înainte de a-l cumpăra din magazinul Lidl (unde mă aştepta cuminte în raft). Dar de obicei funcţionează. În calculator mai am încă un rând de poze cu un ananas cumpărat cu trei săptămâni în urmă din Kaufland, la fel de corect, dar la care vopsirea nu se vede la fel de bine. Pe cele de mai sus le-am ales doar pe baza vopsirii mai clare a alinierilor. Titus “Dole”