O analiză a proiectului de programă de matematică pentru gimnaziu (ian. 2017), cu privire asupra aspectelor metodico-didactice sugerate, sau nesugerate dar necesare, îşi mai are rostul (acum, în martie) decât în sensul boem, de amorul artei, pentru că, la nici două săptămâni de la închiderea aplicaţiei pentru strângerea părerilor profesorilor, comisia de la minister a şi publicat forma finală a programei de matematică pentru gimnaziu.
Astfel, în data de 22 feb. echipa ISE ne-a transmis mulţumiri pentru implicare în consultare, invitându-ne să vizităm aplicaţia cu rezultatele procesului de consultare la adresa http://www.ise.ro/proiectele-de-programe-scolare-pentru-gimnaziu-in-consultarea-specialistilor-si-a-practicienilor . La adresa respectivă am aflat că mai puteam trimite propuneri până în 24 (dar oamenii mai şi lucrează: o mică simulare planificată la a VIII-a şi nu mai ai timp de altceva o vreme). Tot aici am aflat printre altele că profesorii nu s-au prea implicat, cu excepţia celor din Bucureşti, Suceava şi Iaşi. Oare de ce? Totodată, la această adresă se găseşte şi programa „revizuită”, dar la care nu am găsit ulterior nici măcar o singură schimbare semnificativă (de găsit la http://www.ise.ro/wp-content/uploads/2017/01/Programa_mate_clasa_V_VIII_21_02_2017-fg.pdf ).
Totuşi, sunt de părere că trebuie să fim pozitivi şi să privim partea plină a paharului, anume cât de multe aspecte pozitive noi a adus această propunere, şi să analizăm totuşi câteva din aspectele metodico-didactice sugerate de către autori, sau dimpotrivă nesugerate dar necesare de a fi luate în seamă de către profesori. Astfel, multe din gândurile exprimate în acest proiect înspre schimbarea metodicii predării matematicii în gimnaziu sunt atât de novatoare în matematica ultimilor peste 30 de ani în România, încât mă simt nevoit să le reiau în citate (prezentate înclinat) şi să le comentez separat, adăugând şi unele explicaţii suplimentare.
1) Analiza sugestiilor metodologice din proiectul de programă: În procesul de predare-învăţare-evaluare se creează oportunităţi pentru ca elevii să fie conduşi spre conexiuni între diferite teme, între abstract şi practic…(pag 30) Sarcinile de învăţare vor fi eşalonate după gradul lor de dificultate, însemnănd că acestea trebuie să fie eşalonate şi după gradul lor de abstractizare. De pildă, la introducerea operaţiei de putere, la studiul numerelor naturale din clasa a V-a, după cum am arătat în prima parte, eşalonarea trebuie să fie clară pe baza nivelului de abstractizare. Astfel, în prima parte se tratează operaţia din punct de vedere aritmetic, respectând ordinea operaţiilor. Apoi – sugeram la analiza conţinuturilor ca aceasta să se întâmple peste cca. o săptămână – în a doua parte să se treacă la proprietăţile operaţiei de putere, acestea fiind de sorginte algebrică, ele deschizând posibilităţi evidente de încălcare a ordinii operaţiilor.
Să analizăm şi alte astfel de exemple. În propunerea comisiei apare eşalonat studiul geometriei, într-o primă fază cunoaşterea elementelor geometrice mai ales prin intermediul construcţiilor cu instrumente geometrice, într-o a doua fază mai accentuat prin intermediul raţionamentului demonstrativ. În acelaşi sens am propus la analiza conţinuturilor, eşalonarea cunoaşterii numerelor reale din clasa a VII-a în două părţi: în semestrul I o abordare din punct de vedere aritmetic prin calcularea mărimilor în formă practică aproximativă (3,14 pentru π sau 1,73 pentru rădăcina lui trei etc.), iar în semestrul al II-lea abordarea algebrică a numerelor iraţionale, cu folosirea rezultatelor exacte (practicată la ora actuală).
Conform sugestiilor metodologice din acest proiect introducerea conceptelor din cadrul domeniilor de conţinut se va realiza intuitiv, pornind de la exemple din realitatea înconjurătoare…(pag. 30). Sunt într-u totul de acord cu această sugestie; urmez acest principiu de foarte mulţi ani. De exemplu, pentru necesitatea aducerii fracţiilor la acelaşi numitor în vederea adunării acestora, de 25 de ani foloseam următoarea întrebare ca pornire a procesului de gândire: “cât face o jumătate de pâine cu un sfert de pâine?” Întotdeauna primeam răspunsul “trei sferturi de pâine”, din care apoi deduceam lecţia. În urmă cu 8-9 ani am întâlnit primul copil care nu a ştiut să-mi răspundă la această întrebare (la o cercetare mai amănunţită am constatat că în toată viaţa lui văzuse doar pâine gata feliată în pungă de la supermarchet, pâine feliată în stilul “cozonac”).
Ideea este că observăm cum, încet dar sigur, exemplele din realitatea înconjurătoare se restrâng. Cam tot de prin 2010 nu mai găsesc la clasa a VIII-a elevi care să-mi răspundă spontan la întrebarea “câte feţe are un zar?” Am nevoie de această informaţie în cadrul lecţiei despre cub unde consider că formula de arie totală trebuie să o dea elevii pe bază de gândire simplă (ştiu aria unui pătrat; zarul e un cub şi are 6 feţe, deci aria totală a cubului este 6a2). La această întrebare elevii unei clase se împart la ora actuală în două mari categorii: cei care se vede clar că nici măcar nu se gândesc şi cei care încep să numere feţele unui cub imaginar, gest însoţit chiar de o mişcare fizică a capului. Mai de mult nu era aşa; îi întrebam şi primeam spontan răspunsul 6, apoi imediat şi 6a2. De unde această situaţie? Simplu! Ce copil se mai joacă la ora actuală jocuri de mutat piese la care se aruncă cu zarul?
Iată şi un exemplu mai vechi: la începutul anilor ’90 toţi elevii ştiau să socotească cu 25 şi cu vecinii săi, datorită folosirii zilnice a monedelor de 25 bani şi a bancnonetor de 25 de lei. De pildă, orice elev ştia că din 100 lei poţi cumpăra patru ciocolate de 24 lei. La fel, orice elev la descompunerea lui 75 ştia să împartă la 3. Acum nu mai ştiu. La descompunerea lui 75 văd doar divizibilitatea cu 5.
Nu mi-am propus să citez toată partea de sugestii metodologice din prezenta propunere de programă, dar trebuie să scot în evidenţă faptul că magicul cuvânt intuiţie a fost folosit în diferite variante de 19 de ori în această parte. Acest cuvânt mai apare şi în nota de prezentare, dar şi în prezentarea conţinuturilor. Într-adevăr cuvântul magic intuiţie este una din cheile de bază în descuierea gândirii şi trezirea interesului elevilor pentru matematică. În acest sens să reiau un citat prezentat de Eugen Rusu în lucrarea Problematizare şi probleme în matematica şcolară (Ed. Didactică şi pedagogică, 1978), la pagina 37: “Cu intuiţia descoperi, cu logica stabileşti”. (J. Hadamard)
Începând de la reforma uitată din 1980, profesorii au fost vânaţi la propriu, cu ocazia inspecţiilor, să nu mai folosească intuiţia în predare, aceasta nefiind compatibilă cu nou-slăvita predare axiomatică. Rămâne de văzut cum vor reuşi profesorii să-şi seteze predarea pe noua linie, respectiv cum vor fi sprijiniţi prin structurile de formare şi formare continuă în acest sens. Pentru că acum ne putem doar întreba: oare, câţi profesori mai ştiu să folosească intuiţia în predare?
Sugestiile metodologice cuprinse în proiectul de faţă reprezintă din acest punct de vedere documentul cel mai important despre predarea matematicii în gimnaziu emis în ultimul sfert de secol. Reactivarea rolului şi folosirea intuiţiei vine să repare distrugerile de neimaginat din mentalul profesorimii cauzate de implementarea dură a predării riguroase pe baze axiomatice introdusă în şcoli odată cu reforma din 1980 (vezi postarea http://pentagonia.ro/reforma-uitata-o-scurta-descriere/ ). Prin reintroducerea folosirii intuiţiei în predare, distanţându-se astfel de canoanele academice, matematica şcolară românească îşi întoarce din nou faţa către copil (cel puţin la nivel declarativ).
Iată, în continuare, câteva completări la ideile exprimate în legătură cu intuiţia. Predarea intuitivă reprezintă foarte mult pentru elevii claselor V-VI, dar aceasta nu dispare în clasele VII-VIII, aşa cum se poate uşor înţelege din textul de la pag.31. De fapt intuiţia rămâne o componentă majoră a înţelegerii matematicii chiar şi în liceu. Astfel, textul ar trebui să arate mai degrabă aşa: Programele şcolare de matematică pentru clasele a VII-a şi a VIII-a realizează trecerea treptată de la metodele predominant intuitive, abordate în clasele anterioare, la unele mai mature din punct de vedere matematic, cum ar fi definirea unor noi concepte, demonstrarea unor proprietăţi şi aplicarea unor algoritmi de calcul; rămâne însă întotdeauna şi partea intuitivă în clasele superioare gimnaziale. Astfel, aşa cum spre finalul clasei a VI-a, aşteptările sunt ca elevul să poată deja dezvolta raţionamente deductive simple, în mod simetric în clasa a VII-a metodele intuitive fac un mic pas înapoi, dar nu dispar cu totul din ora de matematică.
Legat de ultima frază de la sugestiile metodologice pentru clasa a V-a, eu aş încheia-o astfel: … stimularea şi menţinerea interesului elevilor pentru studiul matematicii se poate face uneori şi prin matematică distractivă (M. Gardner, B.A.Kordemsky, I. Perelman, B.Iosub etc.).
Închei evidenţierea unor puncte pozitive din această propunere cu câteva alte scurte exemple. De pildă, un mare DA! principiului de trecere lentă în clasa a V-a dinspre primar spre gimnaziu. Acesta trece într-un şi mai mare DA! în principiul evoluţiei treptate a unei noţiuni prin predarea în spirală, principiu „citit printre rânduri” în paginile acestui proiect. La fel, un DA! hotărât principiului învăţării prin vizualizare a unor fenomene, pe lângă învăţarea intelectualizată şi prin memorare pură.
Legat de acest ultim principiu doresc să ofer un exemplu sugestiv dintr-o veche carte. La poziţia relativă a două cercuri, lecţie propusă pentru clasele V-VI, aceasta se poate studia deosebit de intuitiv şi practic desenând cele două cercuri cu ajutorul a două monede diferite (merge bine cu 5 şi cu 50 bani). Eu prefer această lecţie totuşi în clasa a VII-a, când le pot cere elevilor o sarcină mai complexă, anume să traseze totodată şi tangentele comune, studiind cum evoluează numărul de tangente comune de la o poziţie relativă la cealaltă. Elevii găsesc cu mare bucurie ideea că în spatele fenomenelor matematice se ascunde deseori un model aritmetic (găsirea principiului ascuns: find the pattern behind it!).
Indiferent dacă sunt principii mici sau mari, aceste principii de bun simţ sunt valoroase prin faptul că au reapărut în programa de gimnaziu după atâţia ani în care au fost neglijate (lista de mai sus nu are în nici un caz pretenţia de a fi exhaustivă).
2) Alte sugestii metodologice de inclus în programă: Am scris foarte mult în acest sens (folosirea inuiţiei de către toată lumea era una din dorinţele la care visam constant), dar voi încerca o scurtă trecere în revistă a celor mai importante aspecte şi metode de predare ce nu le-am găsit enumerate în acest proiect pentru a fi reintroduse în predarea matematicii gimnaziale.
Elevii trebuie din nou să înveţe să gândească, chiar să gândească liber. Ora de matematică nu mai trebuie să fie doar o dresură de învăţare (de frică) a diferitelor exerciţii şi probleme cu metodele de rezolvare pre-oferite de către profesor (pre-date, pre-gătite; ce frumos sună dacă le citim astfel!).
Cel mai important cuvânt absent din acest proiect de programă este problematizarea. Oficial se numeşte predare prin problematizare, dar eu prefer denumirea predare prin descoperire (o formă extremă a primeia). Reintroducerea acestei metode ar fi de lungă durată, majoritatea profesorilor fiind actualmente setaţi să le turuie pur şi simplu lecţia elevilor. Foarte mulţi dintre elevi, pe de altă parte sunt obişnuiţi, sunt dresaţi deja, într-o stare de pasivitate: „De ce mă întreabă pe mine? De unde să ştiu eu cum se face? Să zică ăia buni; să zică el, că el e profesor”. Dar pot depune mărturie: dacă îţi doreşti şi îţi propui cu adevărat, în câţiva ani reuşeşti, iar satisfacţiile ulterioare sunt uriaşe atunci când începe să-ţi reuşească predarea prin descoperire. Lucrarea mai sus amintită a profesorului Eugen Rusu reprezintă în acest sens o lucrare de căpătâi ce ar trebui republicată şi studiată în toate facultăţile ce pregătesc viitori profesori de matematică, respectiv ar trebui parcursă la toate cursurile de formare şi reformare obligatorii la ora actuală.
Desigur, când vorbesc de predarea prin problematizare nu mă refer la acei mulţi profesori care pe parcursul discursului de predare oferă de multe ori pseudo-întrebări: ei întreabă şi tot ei răspund, având astfel pretenţia că lecţia respectivă este interactivă, bazându-se pe un dialog. Nu, dragi colegi, un astfel de pseudo-dialog nu poate fi considerat predare prin problematizare, deoarece elevii sunt într-o profundă stare de pasivitate. Cele mai comice sunt situaţiile când profesorul întreabă „ce teoremă folosim aici?”, iar apoi tot el dă un semi-răspuns: „teorema lui Pi…?” iar elevii continuă „tagora!”. Într-un astfel de caz elevii nu sunt atenţi la oră; ei doar încearcă să mimeze atenţia şi activitatea matematică. Chiar şi cazul când profesorul poartă un dialog real, însă constant doar cu 1-2 elevi cei mai buni din clasă, îi reduce pe restul la starea de pasivitate. Este bine dacă activitatea orei se bazează pe un proces real de problematizare, dar este foarte important ca profesorul să se străduiască să atragă cât mai mulţi elevi în acest proces. Personal, la unele clase acest deziderat îmi reuşeşte mai bine, la altele mai puţin, dar strădania este prezentă tot timpul.
Într-o lucrare precedentă a aceluiaşi profesor, Psuhologia activităţii matematice (Ed. Ştiinţifică, 1969) Eugen Rusu laudă foarte mult matematica proces în comparaţie cu matematica rezultat. Ce sunt acestea? O scurtă explicaţie ar fi că matematica proces este atunci când elevul este parte activă a procesului de creare a lecţiei ce tocmai se învaţă, el compunând lecţa de studiat sub îndrumarea profesorului, pe când matematica rezultat este atunci când profesorul o prezintă pe tablă, ca într-o prelegere, elevul având doar sarcina să o copieze pe caiet şi, în cel mai bun caz, să răspundă la întrebări izolate puse de către profesor. Astfel, de multe ori explicaţiile sunt date, dar şi înţelese doar de către profesor, elevul fiind într-o situaţie similară cu dictarea de către cineva a unui manual. Conectând ultimele două metode active de predare, am putea spune că matematica proces reuşeşte cel mai bine atunci când în procesul de predare se implică tot mai mult şi predarea prin problematizare.
Eugen Rusu vorbeşte uneori şi de matematica vie. Este minunat când elevii ajută la crearea lecţiei, observă anumite lucruri şi îi dau o formă unică şi de nerepetat. Să vedeţi ce interesant este când elevi activi reuşesc să-ţi deturneze lecţia de la planul iniţial şi te trezeşti în final că a ieşit cu totul altceva (nu în sens rău). Aia da lecţie vie! Şi această carte a lui Eugen Rusu ar trebui inclusă alături de cealaltă în studiul şi lectura obligatorie a oricărui profesor de matematică.
Un alt principiu pe care l-am experimentat intens este parcurgerea alternativă a celor doua materii algebră /geometrie (alternativ un capitol de algebră, apoi unul de geometrie). Elevii se concentrează mai bine pe o temă, au patru ore pe săptămână pentru a o înţelege. Se potriveşte aici argumentul acela vechi: dvs., câte cărţi citiţi deodată? Dacă aţi avea de citit aidoma elevilor câte 8-10 cărţi deodată (vorbesc aici doar de manuale), cred că v-aţi bucura dacă una dintre acestea ar lua pauză uneori.
Includerea ideii de parcurgere a unei părţi de matematică în două etape de studiu, una mai elementară, mai intuitivă, cu aplicaţii mai simple, şi a doua mai riguroasă, mai înaltă teoretic şi cu aplicaţii mai superioare, este o idee de mare importanţă pedagogică, cuprinsă în general sub denumirea de predare în spirală. Acest principiu foarte valoros nu trebuie însă limitat doar la nivelul unei clase sau la nivelul unor clase învecinate dar din acelaşi ciclu şcolar. Ţin aici să amintesc desigur parcurgerea geometriei elementare în două etape la conectarea gimnaziului cu liceul: prima, la un nivel elementar intuitiv, pe parcursul claselor gimnaziale VI-VIII, iar a doua, mai matură, cu aplicaţii mai profunde, pe parcursul primelor clase liceale IX-X. Aceasta s-ar putea face desigur prin reintroducerea geometriei elementare în clasele IX-X de liceu, pentru că reducerea nivelului geometriei gimnaziale la un nivel elementar intuitiv a fost făcută în mai mulţi paşi în anii 2000, prezentul proiect reprezentând în acest sens doar recunoaşterea şi organizarea acestui demers pe principii psihologic sănătoase. Eugen Rusu are şi în legătură cu acest subiect unele referiri în lucrarea despre problematizare (de exemplu, la pag. 23: geometria în etapa a doua de studiu, adică în clasele de liceu, şi atenţie, nu vorbea aici de geometria analitică).
Exemplul de mai sus se referă la geometrie, adică la o foarte mare parte de materie. Se pot da aici însă şi exemple mai mici. De pildă, analizând situaţia de câţiva ani buni, în cazul studiului ecuaţiei de gradul II, am convingerea că ar fi benefică următoarea eşalonare a lecţiei. În clasa a VII-a să apară prima oară ideea de ecuaţie cu două necunoscute pe cazuri simple, de tipul x2 = 9 etc. până la (x – 5)2 = 9. În clasa a VIII-a ar apărea diverse cazuri de rezolvări particulare, de pildă x2 – 10x + 16 = 0 / +9, care duce prin cea de sus la dubla ecuaţie x – 5 = ± 3, de unde x1 = 2 şi x2 = 8. Rezolvarea în cazul general, cea cu Δ, ar veni astfel de-abia în clasa a IX-a.
În general, pentru dezvoltarea paletei de metode naturale de predare a matematicii, profesorii ar trebui sprijiniţi cu reeditarea marilor cărţi din domeniu. Pe lângă lucrările lui Eugen Rusu, trebuie măcar amintite şi cărţile lui George Pólya pe care toţi profesorii ar trebui să le aibă în bibliotecă şi să le reia odată la câţiva ani. Sunt cărţi pe care oricând le reciteşti, mai ai ceva de învăţat.
Încerc să închei aici acest eseu fără pretenţia de a fi epuizat nici pe departe subiectul, exprimându-mi încă o dată starea de bucurie generată de această nouă programă.
Prof. C. Titus Grigorovici






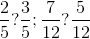 .
.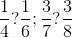 .
.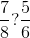 , acestea se pot reprezenta fiecare ca parte dintr-un întreg circular; din compararea celor două desene alăturate se poate stabili care fracţie este mai mare.
, acestea se pot reprezenta fiecare ca parte dintr-un întreg circular; din compararea celor două desene alăturate se poate stabili care fracţie este mai mare. şi
şi  se pot compara reprezentându-le grafic prin împărţirea unui dreptunghi cu lăţimea de 5 şi lungimea de 7 pătrăţele. Pentru prima fracţie împărţim cu o culoare întregul pe lăţime în cinci fâşii din care haşurăm cu această culoare trei fâşii, iar pentru a doua fracţie împărţim întregul pe lungime cu o altă culoare în şapte fâşii din care haşurăm cu această a doua culoare doar patru fâşii. În final avem dreptunghiul întreg împărţit de fapt în 35 de pătăţele, prin cele două culori, şi trebuie doar să numărăm câte sunt mai multe, cele din prima sau cele din a doua culoare. Este clar că această metodă deschide uşa pentru aducerea la numitor comun, dar este recomandabil să lăsăm mai spre final metodele foarte generale (cunoscând o metodă generală, elevul va accepta mai greu alte metode; în acest caz nu ne putem atinge unul dintre obiectivele majore ale unui învăţământ sănătos: deschiderea cât mai largă a minţii elevului).
se pot compara reprezentându-le grafic prin împărţirea unui dreptunghi cu lăţimea de 5 şi lungimea de 7 pătrăţele. Pentru prima fracţie împărţim cu o culoare întregul pe lăţime în cinci fâşii din care haşurăm cu această culoare trei fâşii, iar pentru a doua fracţie împărţim întregul pe lungime cu o altă culoare în şapte fâşii din care haşurăm cu această a doua culoare doar patru fâşii. În final avem dreptunghiul întreg împărţit de fapt în 35 de pătăţele, prin cele două culori, şi trebuie doar să numărăm câte sunt mai multe, cele din prima sau cele din a doua culoare. Este clar că această metodă deschide uşa pentru aducerea la numitor comun, dar este recomandabil să lăsăm mai spre final metodele foarte generale (cunoscând o metodă generală, elevul va accepta mai greu alte metode; în acest caz nu ne putem atinge unul dintre obiectivele majore ale unui învăţământ sănătos: deschiderea cât mai largă a minţii elevului).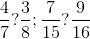 .
. şi
şi  , comparându-le (eventual grafic) cu fracţia intermediară
, comparându-le (eventual grafic) cu fracţia intermediară  , care este destul de cunoscută şi vizual. Deci
, care este destul de cunoscută şi vizual. Deci 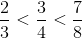 . Un exemplu în acest sens ar fi şi următorul: fracţiile
. Un exemplu în acest sens ar fi şi următorul: fracţiile  şi
şi 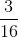 pot fi comparate cu
pot fi comparate cu  .
.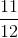 şi
şi 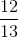 , diferenţele până la un întreg sunt
, diferenţele până la un întreg sunt 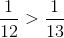 . Este evident că
. Este evident că 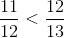 .
. .
.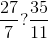 .
.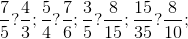
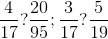 .
. care conectează în mintea elevului cu semnul împărţirii (un punct în plus înseamnă împărţire exactă), dar rămâne pe calapodul de gândire obişnuit (numărul mare este divizibil cu numărul mic, evitând inversarea cerută de scrierea cu bară).
care conectează în mintea elevului cu semnul împărţirii (un punct în plus înseamnă împărţire exactă), dar rămâne pe calapodul de gândire obişnuit (numărul mare este divizibil cu numărul mic, evitând inversarea cerută de scrierea cu bară).