Profesorii de matematică ce s-au oferit (?) sau au fost aleşi (?) de a susţine lecţiile din cadrul emisiunilor teleşcoala sunt într-o situaţie delicată: pe de o parte acţiunea poate reprezenta o platformă de lansare deosebită spre o recunoaştere mai largă în cariera didactică; pe de altă parte postura respectivă “în lumina reflectoarelor” este una deosebit de ingrată. De prima parte nu-mi fac griji, dar permiteţi-mi să explic la ce mă refer cu partea ingrată.
Filozofia impusă în anii ’80 de către autorităţile comuniste susţinea că întotdeauna este loc de mai bine. Era o metodă prin care oricine putea fi criticat, astfel încât nimeni să nu se simtă sigur în situaţia sa. Încet, dar sigur, după Revoluţie ideea a prins la tot mai mulţi concetăţeni, generalizându-se ca metodă democratică de dezbatere şi analiză.
Într-adevăr, dispoziţia de a critica pe cel de alături a prins foarte bine în societatea românească. Mulţi oameni se simt bine când îl critică pe celălalt, având astfel un sentiment de superioritate faţă de cel criticat. Astfel au apărut oameni care practică această “artă a criticatului” cu deosebită satisfacţie. Chiar a devenit un gest de “bon ton” în a-i contesta celuilalt afirmaţiile, de a-i arăta de fapt cum stau lucrurile, că tu te pricepi mai bine, după principiul “îţi spun eu cum stau lucrurile!”.
Ca urmare a acestei atitudini generalizate, orice apariţie într-o oră deschisă a unui profesor este deosebit de minuţios pregătită, pentru a reduce la maxim şansele de a oferi asistenţei posibilitatea de a te critica (iar asistenţa tradiţională matematică de-abia aşteaptă o astfel de ocazie!). Ne dăm seama în aceste condiţii ce este în sufletul unui profesor care apare într-o lecţie în faţa întregii ţări, postată apoi pe youtube astfel încât să-ţi poată oricine diseca vorbele.
Eu ştiu câte ceva despre acest subiect pentru că am avut în familie o astfelde experienţă: mama mea a ţinut o lecţie de Teleşcoala la sfârşitul anilor ’70, şi ţin minte ce zdroabă a fost atunci cu pregătirea fiecărui cuvânt din lecţia respectivă (cartea din care tatăl meu a conspectat la greu pentru a o ajuta pe mama să pregătească lecţia este acum la mine: nici nu o bag în seamă, dar atunci era la mare apreciere).
Revenind la lecţiile din aceste zile, cum spunea şi soţia mea: sigur nu-i poţi mulţumi pe toţi; sigur se vor trezi mulţi deştepţi care să-i critice pe colegii care s-au încumetat la aşa o acţiune “cu tente sinucigaşe”. Şi atunci ce faci ca profesor ce urmează să susţii o lecţie cu audienţă (redusă sau extinsă)? Ce poţi să faci pentru a preîntâmpina pe cât se poate apucăturile de a te critica din partea celorlalţi? Simplu! Îţi pregăteşti o lecţie cât mai completă din punct de vedere teoretic; o încarci cu toate detaliile ca să nu poată să se trezească “nuş-ce deştept” să te completeze sau să te critice. Apoi vin gândurile la adresa profesorilor obsedaţi de probleme “de nivel ridicat, pentru elevii buni şi foarte buni”. De ce? Pentru că aceştia – cei cel mult 10% din populaţia şcolară – au reprezentat preocuparea principală a şcolii matematice româneşti timp de 40 de ani.
Ştiindu-te astfel asigurat din cele două direcţii predilecte de unde poţi fi criticat, te apuci apoi să susţi lecţia stabilită. În acest moment apare ciudatul de la Cluj, care tot scrie pe pentagonia şi pune întrebarea încuietoare: Deci, pentru cine sunt făcute aceste lecţii? Că pentru majoritatea elevilor nu sunt croite, asta-i sigur. Aceştia pur şi simplu nu le vor înţelege. Sunt prea încărcate de elemente teoretice, într-un limbaj excesiv de riguros, iar ¾ din aplicaţii se adresează celor cel mult 10% din populaţia şcolară (George Pólya susţine că aceştia ar reprezenta de fapt doar 1%, dar noi ştim desigur mai bine, românii sunt mult mai deştepţi decât restul planetei, aşa că le spun în continuare 10% pentru a nu deranja lectura restului de articol). Părerea mea este că sunt eventual gândite pe gustul profesorilor, au multe aplicaţii pe nivelul elevilor de vârf, dar sigur nu sunt pentru marea parte a elevilor.
Acum, eu sunt într-o situaţie foarte neplăcută; mă simt ca o babă ce stă pe banca din faţa casei şi îi critică pe cei ce lucrează, mergând în sus sau în jos pe uliţă. În acest sens refuz să încep să dau exemple la ce mă refer când spun aceste lucruri, dar pot să spun măcar următoarele elemente. Tehnic, eu m-am rupt încet dar sigur de stilul de predare uzual în şcolile româneşti, pornind în urmă cu aproape un sfert de secol într-o reformă “de unul singur”, preluând din străinătate, dar şi din matematica românească dinainte de 1980, cât am putut de mult şi evoluând astfel într-o formă de predare plină de empatie şi respect faţă de elevi, atât cei buni cât şi cei slabi.
Singurele contacte pe care le-am mai avut cu forma de predare din şcolile tradiţionale este una “second hand” prin intermediul puţinelor lecţii ale elevilor din alte şcoli care mai vin să-mi ceară ajutorul. Fiind astfel personal atât de departe de elementele considerate a fi de dorit de către mentalitatea generală, este evidentă reacţia mea la vederea acestor ore televizate: cu greu am urmărit cap-coadă o astfel de lecţie; a doua am urmărit-o pe sărite, iar la treia două trei momente şi gata.
Cum zice o vorbă urâtă, “simţeam că dau în icter” din cauza elementelor din aceste ore, pentru că simţeam doar preocuparea pentru completitudinea exprimării de specialist şi neapărata prezenţă dominantă a exerciţiilor pentru elevii de 9-10. Îmi închipuiam ce înţeleg, mai degrabă cât de puţin înţeleg majoritatea elevilor, cei slabi şi cei mulţi din blocul central al clopotului lui Gauss, văzând asemenea etalare teoreticistă, la care atenţia îi lasă baltă după 5-6 cuvinte riguros aranjate, iar apoi văzând toate exemplele ciudate, fără etalarea nici măcar a unui exerciţiu de bază tipic în lecţie sau la temă.
Şi încă o dată întreb: pentru cine sunt aceste lecţii? Pentru că sigur nu sunt pentru elevii obişnuiţi. Poate sunt pentru autorităţi, că să nu putem spune că n-au făcut nimic. Nu ştiu cum să zic, dar simt că pentru majoritatea elevilor sunt inaccesibile.
Eu de mult am un fel de viziune, iar aceasta mi s-a confirmat din plin cu această ocazie. De mult eu aveam impresia că profesorii de matematică predau într-un mod extrem de riguros, ca şi cum în spatele clasei ar fi o cameră de luat vederi (cu microfon desigur) conectată constant la inspectorat, iar inspectorul de matematică n-are nimic mai bun de făcut decât să comute de la o şcoală la alta, de la un profesor la altul, verificându-l dacă se exprimă riguros. Pentru colegii care au ajuns să predea aceste lecţii de teleşcoală, pentru ei aceste sentimente s-au materializat la modul cel mai concret (ieşind din zona unei impresii poate subiective), iar în acest sens singura lor preocupare în aranjarea lecţiei este desigur de a ieşi “basma curată” din toată tărăşenia (cu atâtea perechi de ochi şi de urechi aţintite asupra ta, nici nu ai ce să gândeşti altceva).
Închei totuşi cu două exemple, iar ca să fiu “politically correct”, voi da un exemplu pozitiv şi unul negativ (da, am găsit în sensul celor spuse mai sus şi un exemplu pozitiv; cât despre cel negativ, din multitudinea de exemple de care m-aş putea lega, l-am ales pe cel care m-a indignat cel mai mult, anume pe cel care reprezintă după părerea mea cea mai gratuită răutate la adresa elevului de rând).
În sens pozitiv, mi-a sunat în urechi, pe când nu prea mai aveam răbdare, cum colega dicta calculele din teorema lui Pitagora: pătratul ipotenuzei este egal cu suma pătratelor catetelor. Deci nu-i totul pierdut; lupta merită continuată: la postul naţional cineva a renunţat la cuvântul lungime, exprimând teorema lui Pitagora în cel mai simplu mod, corect dar totuşi neîncărcat.
Ca exemplu negativ, am descoperit cu durere, chiar cu indignare, următoarea situaţie: în loc de succesiunea naturală: x2 = 9 => x = ± 3, se alege tot mai des mult mai “preţioasa rezolvare” x2 = 9 => | x | =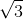 
=> x = ± 3. Cum arată o astfel de rezolvare în lecţia televizată (lecţie despre care autorităţile susţin că este accesibilă tuturor elevilor din ţară, inclusiv celor care nu au acces la internet)? Păi, simplu, uite aşa: (2x + 1)2 – 9 = 0 <=> (2x + 1)2 = 9 => | 2x + 1 | = 
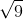=> 2x + 1 = ± 3 etc. Clar, nu? Întrebaţi pe un copil din vecini, dar nu pe unul dintre aceia foarte buni, şi vedeţi ce vă spune. Tare aş vrea să aud justificarea unui “pedant” explicând la ce naiba ajută modulul acela în această situaţie
Oameni buni! Când veţi înţelege că un modul cu ceva necunoscută înăuntrul său îi sperie pe cel puţin 60-70% din elevii de gimnaziu? De ce să includem în rezolvare acel modul în compania unui radical, când se poate şi fără? Eu asta numesc o răutate gratuită la adresa elevilor, iar matematica predată în România este plină de astfel de exemple. Este clar că nu are nimeni curajul să interzică astfel de situaţii prin lege. Oare, când se va înţelege că datoria noastră este în primul rând să predăm o matematică cât mai accesibilă unei pături cât mai largi de populaţie şcolară? Abia după ce cei mulţi vor fi înţeles lecţia de bază, abia apoi putem veni cu tot felul de jiumbuşlucuri matematice.
Da! Aplic aici un principiu învăţat de la colegii din Germania care ne mai vizitează să vadă cum merge Waldorfu’ pe la noi: după o vizită la un dascăl la oră, nu-şi permit mai mult de două aspecte negative de evidenţiat şi asta doar dacă au reuşit să evidenţieze şi două aspecte pozitive. Eu mă opresc însă la 1 : 1. Şi totuşi, pentru cine sunt aceste lecţii? CTG