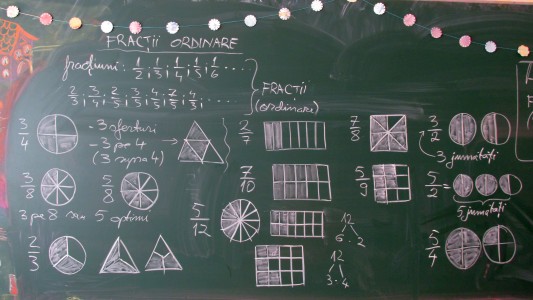Anul 1981 marca ultima apariţie editorială pentru profesorul emerit Abraham Hollinger. În prefaţa acestei cărţi există un paragraf fascinant, din care putem înţelege şi citi printre rânduri foarte multe aspecte importante. În postarea precedentă am prezentat acest paragraf pentru a putea inţelege gândurile profesorului Hollinger în integralitatea lor, aşa cum a considerat dânsul a le exprima în contextul finalului de perioadă metodico-didactică a anilor ’60 -’70.
Reiau încă o dată anumite pasaje din acel citat, lărgind însă pasajul şi completându-l cu anumite cuvinte cheie pentru a accentua anumite aspecte. Astfel, gândurile şi preocuparea dânsului erau îndreptate în special către elevul mijlociu (!) care trebuie să îşi însuşească cel puţin un minim de cunoştinţe şi să fie capabil să le aplice (…). Ideea de lucru a fost de a propune elevilor numeroase exerciţii simple, chiar foarte simple în comparaţie cu cele uzuale (la vremea respectivă).Iată cum ne explică dânsul: Prin aceasta elevul se obişnuieşte treptat cu diferitele situaţii noi (…) Astfel de exerciţii nu prea există în cărţile pe care le cunosc; le-am compus. Pentru a da muncii elevului un ritm mai viu, am dat de cele mai multe ori şi figura, ca elevul să poată trece imediat la rezolvare; ele sînt gândite ca un fel de exerciţii orale. (…) Aceste probleme se găsesc la începutul fiecărui paragraf. (…) (A. Hollinger, Probleme de geometrie pentru clasele VI-VIII, Ed. Didactică şi Pedagogică, 1982; din Prefaţă, pag. 3-4).
Culegerea respectivă este una de geometrie; profesorul Hollinger se plânge că la geometrie saltul de la introducerea noilor noţiuni la aplicaţii este prea mare în comparaţie cu situaţia de la aritmetică sau algebră. Părerea mea este că în anii ’80 (deci contemporan, dar şi după culegerea respectivă) acest decalaj a fost rezolvat, dar nu în sens pozitiv, ci în sens negativ: la ora actuală nici la aritmetică, nici la algebră intrarea într-o temă nouă nu mai este de obicei accesibilă. La ora actuală toate domeniile de studiu matematic preuniversitar sunt extrem de abstracte, cu trepte de intrare mult prea înalte pentru elevul mijlociu, puse de la început – aparent – ca o piedică insurmontabilă pentru majoritatea elevilor.
Eu studiez din anii ’90 această culegere, iar pasajul respectiv îmi sună de fiecare dată proaspăt şi logic: noi trebuie să venim în întâmpinarea elevilor obişnuiţi (a elevului mijlociu, cum spunea Hollinger), pentru sprijinirea înţelegerii matematicii. Mai ales atunci când mare parte din preocupările organizatorilor învăţământului matematic – oficiali sau neoficiali – sunt îndreptate cu predilecţie către elevii de vârf şi activităţile matematice ale acestora (aşa-zisa excelenţă), mai ales atunci consider că este de datoria mea să mă străduiesc mai mult şi să vin şi mai hotărât în întâmpinarea elevului obişnuit cu lecţiile mele.
În continuarea primului aliniat din prefaţa acestei culegeri Hollinger ne spune că el s-a preocupat de fapt în a genera, a compune, a poziţiona nişte trepte suplimentare mai mici la începutul fiecărei teme (lecţie, capitol), sub forma unor exerciţii ce pot fi rezolvate oral, însoţite de figuri menite de a ajuta vizualizarea fenomenului nou de către mintea şi imaginaţia încă nepornită, neîncălzită, neexperimentată a elevului novice în acea temă de studiu. Aceşti paşi trebuie făcuţi la începutul fiecărei teme noi, pentru a asigura, a garanta accesibilitatea acesteia pentru toţi elevii (la începutul fiecărui capitol, dar şi oriunde apare ceva cu adevărat nou). Dânsul a făcut acestea la geometrie, pentru că în anii ’60 -’70 acolo a simţit nevoia de aşa ceva. Actualmente această nevoie este la fel de prezentă şi la algebra gimnazială, chiar şi la primele lecţii de aritmetică din clasa a 5-a.
*
În prima postare pe această temă am vorbit despre introducerea unei trepte suplimentare pregătitoare în sensul efectuării împărţirii în cap, necesară apoi la descompunerea numerelor în factori primi. Încheiam această primă postare cu ideea că mai am şi alte exemple. Aş dori să vă prezint în acest sens gestul de inserare a noţiunii de fracţiune înaintea studiului despre fracţii ordinare, aşa cum îl înţeleg eu acum, după câţiva ani de preocupare în acest sens.
Elevii fac cunoştinţă cu fracţiile (cele ordinare) în timpul petrecut cu d-na învăţătoare. La reluarea acestora în clasa a 5-a este oricum binevenită o recapitulare. Nici nu iau în discuţie posibilitatea ca învăţătoarea unui elev să nu fi lucrat foarte bine fracţiile pentru că nu se pricepe (acest subiect oricum nu mă priveşte în mod direct). La fel, nu iau în discuţie situaţii de tipul că în clasa a 4-a au fost în anul trecut cazuri de predare online exact la fracţii, iar copilul pur şi simplu n-a prins ideea. Aş porni însă discuţia de la faptul că poate avem o clasă cu copii provenind de la mai multe învăţătoare, iar aceştia ar trebui aduşi la un acelaşî nivel de cunoştinţe de bază. Totodată pot să iau in calcul şi ideea unui copil care s-a mai maturizat între timp şi, poate acum, la o a doua trecere, cu răbdare, dar şi cu mai mult profesionalism matematic, elevul reuşeşte să le înţeleagă mai bine. Da, şi neapărat trebuie pornită discuţia de la faptul că vorbim despre majoritatea elevilor, nu despre vârfuri, adică despre “elevul mijlociu”, cum spunea Hollinger
Traduc această afirmaţie: cu alte cuvinte, este de datoria mea să-i luminez pe majoritatea elevilor (blocul principal din Clopitul lui Gauss), să-i fac să plece acasă cu lucrurile înţelese; nici nu vreau să evoc acele – din păcate mu-u-u-ulte – cazuri când lectia este atât de abstract predată, încât elevul are nevoie acasă de o nouă predare, de explicaţii individuale care să-l scoată “din ceaţă”. Dacă se mai pricepe un părinte, încă treaba mai merge cumva; din păcate, în ultimă instanţă de fapt este nevoie tot mai des de ore particulare pentru a putea duce matematica de la clasă (asta întâmplându-se tot mai des chiar din clasa a 5-a). Apropos: apogeul acestui fenomen deplorabil se atinge atunci când apare la o şcoală particulară unde părinţii plătesc oricum bani grei, iar apoi toţi elevii au nevoie de ore private pentru a face faţă matematicii de la şcoală! (A se înţelege ad-literam! Şi da, avem la Cluj şi aşa ceva! Desigur că şi copiii sunt tot mai sensibili, dar acesta este alt subiect, la care îmi propun să vin cât de repede)
Predarea fracţiilor ordinare trebuie să pornească neapărat de la multe exemple de vizualizare a diferitelor cantităţi reprezentate prin fracţii. Cele mai bune par a fi cele în formă de cerc (măr, lipie, pizza etc.), dar este bine ca elevii să primească şi alte exemple: ca pătrat (ce merge împărţit clar în 2, 4, 8 părţi egale), ca dreptunghi (similar cu pătratul), ca dreptunghi similar cu o pâine dreptunghiulară feliată, eventual chiar ca dreptunghi împărţit şi pe lungime şi pe lăţime (ducând spre ideea de arie a dreptunghiului; de exemplu un dreptunghi de 2 pe 5 pătrăţele pentru zecimi). La fiecare dintre acestea vom colora o parte dintre bucăţele, evidenţiind astfel o fracţie dintr-un întreg. Toate noţiunile iniţale (fracţii subunitare, supraunitare, echivalente, compararea lor etc.) pot fi apoi deduse, explicate, justificate şi înţelese prin reprezentarea în imagini ce se desenează foarte uşor. Toate regulile se deduc în urma unei analize iniţiale pe unul-două exemple desenate, vizualizate, reprezentate grafic aşadar.
Un exemplu deosebit de bun în acest sens (nu vreau să spun că singurul) îl reprezintă Manualul pentru clasa a V-a de Matematică din 2002 (?) de la Editura Sigma, cu o echipă de autori condusă probabil de D-na Mihaela Singer. Întreaga parte despre fracţii ordinare este înţesată de reprezentări grafice ale fracţiilor alese ca exemple, evidenţiindu-se astfel vizual fenomenele studiate în fiecare moment (nu cunosc situaţia actuală a implicării acestei edituri la nivelul clasei a 5-a, aşa încât mă opresc aici cu acest comentariu).
Cam acesta ar fi nivelul la care s-ar putea gândi profesorul de matematică în sensul strădaniei de a explica lecţia de matematică în mod cât mai accesibil şi clar elevilor, de a veni cu nivelul începutului lecţiei cât mai jos spre nivelul real al multor elevi, pentru a avea garanţia că îi ia pe cât mai mulţi în noua temă. Faţă de acest nivel de strădanie, “zeii matematicii” mi-au îndrumat gândurile şi ideile spre un pas suplimentar, pe care cu timpul am ajuns să-l înţeleg ca fiind de făcut înaintea lecţiei de introducere a fracţiilor ordinare. Încerc să detaliez situaţia cunoscută de către toată lumea, pentru a prezenta apoi pasul despre care doresc să vă vorbesc.
Oricum ai aborda noţiunea de fracţie, trebuie de fapt să le aduci elevilor în conştienţă clară rolul celor două numere implicate de obicei în scrierea unei fracţii – numitorul şi numărătorul – pentru ca aceştia să înţeleagă ce face fiecare din cele două numere (nici nu amintesc aici încă despre al treilea număr, anume despre scoaterea întregilor din fracţie). Fie că le dă exemple, fie că le dă o definiţie seacă pe bază de litere, profesorul ar trebui să le explice ce face fiecare dintre ele. Din păcate tot mai des întâlnesc situaţii în care se pare că nici măcar atât nu se străduiesc unii colegi.
Ca o divagaţie înalt filozofică despre didactica introducerii noilor numere, observ aici din păcate că modelul impus la introducerea / predarea numerelor complexe, în programa din manualele de liceu apărute la sfârşitul anilor ’70, spre deosebire de forma precedentă, acest model s-a generalizat în mod bolnav până la nivelul clasei a 5-a. Să detaliez puţin: cum era modelul precedent, valabil până în 1978? Numerele complexe se construiau de la notarea rădăcinii pătrate din numărul –1, notată pentru comoditate cu “i” (de unde i2 = –1), din care apoi se deduceau toate proprietăţile acestuia (puterile lui i) şî toate proprietăţile de operare cu numerele complexe z = a + bi (în principal adunarea şî înmulţirea etc.). Prin manualele din 1978 numerele numerele complexe se introduc axiomatic, sub forma stupidă a unor perechi ordonate ale căror operaţii respectă renumitele proprietăţi pentru sumă şi produs, proprietăţi ce apar în faţa elevului în mod total artificial, fără nici cea mai mică logică pentru mintea elevului. În mod similar, după 40 de ani, la ora actuală există deja profesori care nici nu se mai gândesc să le explice elevilor de a 5-a în mod clar ce face numitorul şi ce face numărătorul (scuze că nu intru în explicarea acestor afirmaţii; am făcut-o cu alte ocazii).
Da, există profesori care le spun cum se numesc, iar apoi trec direct la lecţii noi, fără a se gândi că elevii trebuie să şi înţeleagă despre ce este vorba. Cred că totuşi majoritatea au impulsul de a le explica, doar că o fac numai oral, pe fugă, iar din aceste explicaţii nu rămâne nimic scris, nu apare nimic în lecţia din caiet, aceste explicaţii pierzându-se în general datorită nivelului slab de atenţie al elevilor, datorită faptului că unii vin la ora de matematică doar ca să copieze de pe tablă, mulţi fiind rămaşi în urmă în momentul respectiv, cu scrisul de pe tablă al titlului, cu ascuţitul creionului etc.
Părerea mea este că lecţiile de matematică ar trebui să conţină componente clare în sensul înţelegerii şi conştientizării de către elev a rolului fiecărui număr din componenţa unei fracţii. Primul pas în înţelegerea fenomenului de fracţie este conştientizarea de către profesor a ordinii logice a apariţiei celor două numere în procesul de naştere a unei fracţii. Deci, care din cele două numere apare primul? Este evident că numitorul, acesta reprezentând numărul părţilor egale în care se împarte întregul. De-abia apoi apare numărătorul, acesta spunându-ne câte astfel de părţi vor fi luate pentru a forma fracţia respectivă. Din păcate însă, chiar scrierea şi citirea fracţiilor este pe dos: se spune mai întâi câte părticele sunt şi doar apoi ce fel de părticele sunt (două treimi; trei cincimi; cinci pătrimi etc., aşa fiind structurată exprimarea în limbile uzuale). Or, pentru a evita o învăţare automată, pentru a genera o înţelegere clară şi o gândire sănătoasă, noi trebuie să ne străduim ca elevii să înteleagă cu adevărat “mesajul”, rolul fiecăruia din cele două numere componente ale unei fracţii.
Strădania de a reprezenta grafic cât mai multe fracţii la început este cu totul în acest sens. Dimpotrivă, este evident că un profesor care minimalizează rolul acestei etape, uneori până al neparcurgerea ei, îi împinge pe elevi spre neînţelegerea matematicii.
Cele spuse aici despre “ordinea” logică în care apar cele două numere – mai întâi numitorul şi doar apoi numărătorul -, această ordine se regăseşte chiar şi în ordinea apariţiei şi dezvoltării noţiunii de fracţie de-a lungul istoriei (cel puţin a istoriei matematicii, aşa cum este aceasta cunoscută din izvoarele existente).
Primul care a apărut este numitorul; mai exact primele apărute în acest sens sunt fracţiunile: jumătatea, treimea, sfertul, cincimea etc. Nu câte cincimi, ci doar noţiunea de cincime (fracţiile de tipul 1/2; 1/3; 1/4; 1/5 etc., care mai sunt numite în mod prea-preţios fracţii alicote). Acestea au fost găsite pentru prima dată în papirusul Rhind, aflat în custodia British Museum la Londra.
Într-un proces de câţiva ani, în mintea mea s-a generat ideea introducerii fracţiunilor ca primă lecţie a acestui capitol. Introducând pentru început doar fracţiunile (1/2; 1/3; 1/4; 1/5 etc.) şi folosindu-le timp de cel puţin o oră, elevul are timp să se obişnuiască cu rolul numitorului, care este cel mai abstract dintre cele două numere (un 3 la numărător chiar reprezintă faptul că sunt 3 bucăţi, pe când un 3 la numitor îmi spune că este vorba despre treimi, cu implicaţii ciudate pe viitor: de pildă treimea este mai mare decât cincimea, deşi 3-ul este mai mic decât 5-ul).
Pentru a face cu adevărat acest pas, profesorul trebuie să evite simpla explicaţie; la aceasta vor reacţiona doar elevii cu o gândire mai raţională. Majoritatea elevilor vor înţelege însă doar dacă vor şi face cu adevărat paşi de fracţionalizare a unui întreg, iar asta se poate face concret doar prin desenele despre care am vorbit la început (acestea având şi avantajul că rămân în caiet, fiind vizualizabile şi ulterior). Mulţi colegi profesori vor vedea un astfel de demers ca pierdere de vreme, dar eu consider că este un timp investit cu rost în înţelegerea fenomenului de către majoritatea elevilor, iar cu timpul acesta se va transforma în timp câştigat pentru gândirea copiilor.
Odată introduse noile noţiuni, cunoscute de fapt parţial din clasa a 4-a (treimea, sfertul, şesimea, şeptimea, optimea, zecimea etc.), ar fi bine să facem ceva cu acestea, dar încă nu în sensul fracţiilor, adică al multiplicării fracţiunilor. Vorbeam de “zeii matematicii” şi iată ce soluţie am găsit eu în acest sens. În reportajul The Story of Maths realizat şi prezentat de către profesorul Marcus du Sautoy de la Universitatea din Oxford şi produs de canalul BBC FOUR, acesta ne prezintă cum ar fi efectuat vechii egipteni împărţirea a 9 lipii la 10 oameni. Este un procedeu inedit pentru noi, care ne arată cum funcţiona gândirea vechilor egipteni în sensul fracţionalităţii (cel puţin încearcă acest lucru). Un al doilea punct de inspiraţie l-au reprezentat articolele profesorului Ernst Bindel din anii ’60 (autor cunoscut în matematica şcolilor Waldorf), dar am găsit referiri despre acestea şi la Florica T. Câmpan.
Merită să zăbovesc puţin la această problemă – împărţirea a 9 lipii la 10 oameni – , mai ales că eu fac la ora respectivă un adevărat spectacol. Concret, pentru a vizualiza cât mai clar fracţiunile şi felul în care acestea compun soluţia problemei, eu mă duc la ora de matematică dotat cu toate cele necesare: un pachet cu suficiente lipii, un ştergar, două funduri de lemn mari şi foarfeca din bucătărie. După ce am desenat la începutul orei fracţiunile (eu pe tablă şi elevii în caiete), facem un moment organizatoric. Îmi aranjez o bancă central în faţa clasei, astfel încât elevii să poată veni în semicerc în jurul meu, pe cel mult două rânduri, aşa încât să vadă fiecare de aproape ce voi face în continuare.
După ce îmi aranjez cele necesare încep: cum ar fi făcut vechii egipteni? Păi împărţeau în primul rând câteva lipii în jumătăţi. Aici încep să tai lipii în jumătăţi cu foarfeca. Câte lipii trebuie să tai? întreb eu în timp ce tai, iar răspunsul vine imediat: cinci lipii. Aşa, deci acum am aici un teanc cu zece jumătăţi de lipie. Ce fac în continuare?Păi iau următoarele fracţiuni la rând, adică treimile … Mă opresc aici cu redarea dialogului, mizând pe faptul că vă veţi putea închipui şi dvs. restul pe baza pozelor tablei. După ce rezolv problema fizic, pe masă, tăind fracţiuni de lipie, elevii merg la locuri şi reluăm tot procesul în scris, eu pe tablă iar elevii în caiete.
Accentuez aici faptul că fac acest proces de două ori: o dată fizic, tăind lipii în faţa elevilor, iar a doua oară desenând cele întâmplate pe tablă. Astfel am convingerea că am făcut tot ce se putea omeneşte posibil şi într-un mod cât mai interesant, astfel încât elevii să înţeleagă şi să li se fixeze care este rostul numitorului, ce anume face acesta (numărătorul urmând să apară ulterior, adică cel mai devreme ora următoare, deci într-o altă zi).
Spre deosebire de alţi ani, iarna asta am avut o întâmplare inedită. La începutul dialogului evocat, la prima întrebare, până acum eu întrebam: cum ar fi făcut vechii egipteni? şi tot eu trebuia să şi răspund: Păi împărţeau în primul rând câteva lipii în jumătăţi. Anul acesta însă, m-am trezit cu răspunsul potrivit de la un prichindel. Este vorba de un băieţel din părinţi sirieni. Am rămas mască: el nu ştia problema, dar cumva creierul său a funcţionat exact aşa cum îmi povestise Marcus du Sautoy că ar fi făcut vechii egipteni. Fabulos!
În imaginile cu tablă ataşate găsiţi lecţia despre fracţiuni, aşa cum am făcut-o eu anul acesta la una din clase. În acea oră am reprezentat pe lângă fracţiuni şi câteva fracţii (la clasa paralelă le-am prezentat cu totul separat).
Ataşez în continuare şi lecţia a doua (de la clasa paralelă, unde fracţiile au apărut doar în următoarea oră) pe baza căreia se vede cum am realizat transferul reprezentării grafice a fracţiilor, astfel încât fiecare elev să înţeleagă cu adevărat noţiunea de fracţie, ce anume reprezintă fiecare dintre cele două numere ce formează o fracţie. Se vede cum eu dau explicaţia teoretică în mod rezumativ, la finalul lecţiei, nu la început, aşa cum se obişnuieşte actualmente (copilul cunoaşte fracţiile intuitiv, iar apoi sintetizăm noţiunea).
Pentru cei care doriţi să aprofundaţi noţiunea de fracţii alicote (se pare că aşa s-ar numi ele oficial, deşi eu le-am spus fracţiuni, căutând o denumire mai accesibilă elevilor), ataşez şi un articol la care am lucrat intens prin 2013-2014, dar încă nepublicat. Nu pot susţine că actualmente mai sunt într-u totul de acord cu toate elementele din acel eseu, dar pentru eficienţa faţă de curiozitatea unora dintre dvs. merită să îl prezint chiar şi aşa cum a rămas în calculatorul meu, în varianta scurtă a muncii întreprinsă în acei ani (cu scuzele de rigoare am şi o amintire vagă că ar exista o greşeală la unul din exemple). Sunt sigur că cei care se vor entuziasma de subiect, vor putea găsi şi alte aspecte necuprinse în acest eseu. CTG