Există zece feluri de oameni: cei care înţeleg sistemul binar şi cei care nu-l înţeleg.
Happy Birthday to me!

Mulţumesc de cadouri!
Tocmai ce am împlinit 100 de ani! Ghiciţi în ce bază de numeraţie este exprimată astfel vârsta mea.
P.S. Ce bună ocazie să le explic elevilor ce-i cu bazele de numeraţie! Mai ales când le spun că şi prietena fiului meu, care tocmai termină facultatea, împlineşte 100 de ani, dar în altă bază (oare în care?). Asta pentru a-i lămuri pe elevi ce-i cu exprimarea aia de neînţeles din anumite probleme: “numărul scris în baza 10” (rămasă ca o cicatrice în exprimarea riguroasă şi pretenţioasă a profesorilor, de pe vremea când bazele de numeraţie se studiau puternic în clasa a V-a). Este clar că se pot găsi diferite conexiuni, de pildă faptul că 100 din diferite baze reprezintă de fapt pătratele perfecte folosite de elevi în mod obişnuit, adică în baza 10.
Reforma uitată
(o scurtă descriere)
La începutul anilor ’80 a avut loc o amplă reformă a predării matematicii în România, cu efecte negative asupra capacităţii elevilor de a înţelege şi folosi noţiunile predate. Din dorinţa de a ridica nivelul performanţei olimpice, sistemul şi-a confruntat elevii cu un mod de predare a matematicii mult peste puterea de înţelegere vărstei. Ca urmare, tot mai mulţi elevi au absolvit şcoala cu deficienţe serioase în înţelegerea noţiunilor de bază din matematică, dar şi de gândire în general. A urmat un lung şir de încercări de remediere a situaţiei, prin noi reforme şi noi programe. Acestea însă nu rezolvă cu nimic problema de fond, deoarece nu pornesc de la înţelegerea profundă a situaţiei.
După publicarea în februarie a eseului despre reforma uitată din 1980 am primit unele observaţii, mai ales legat de necesitatea unei variante mai scurte şi mai accesibile publicului larg. Pentru accesibilizarea ideilor la prima lectură, vă prezentăm o nouă variantă mai “comercială” a eseului despre aceasta reformă şi despre modificările care au îmbolnăvit matematica şcolară românească ulterioară.
*
Suntem obişnuiţi să considerăm matematica o activitate doar pentru cei aleşi de soartă, deşi este obligatorie şi are alocat, alături de limba română, cel mai mare număr de ore până la clasa a VIII-a. Toţi ceilalţi se chinuie prin şcoală la orele de matematică, sunt traumatizaţi de matematică şi în nici un caz nu apucă să beneficieze de aspectele formatoare ale matematicii. Ce înseamnă cei aleşi şi ce înseamnă toţi ceilalţi? Las cititorului dreptul de a trage o linie relativă de demarcaţie în graficul cunoscut ca Clopotul lui Gauss. Părerea mea este că doar o parte prea mică a ramurii din dreapta face faţă onorabil matematicii din şcolile româneşti, iar asta se întâmplă de foarte mult timp. Ultimii 20-30 de ani au fost clar marcaţi de acest dezechilibru înjositor cu urmări grele la nivelul majorităţii elevilor.
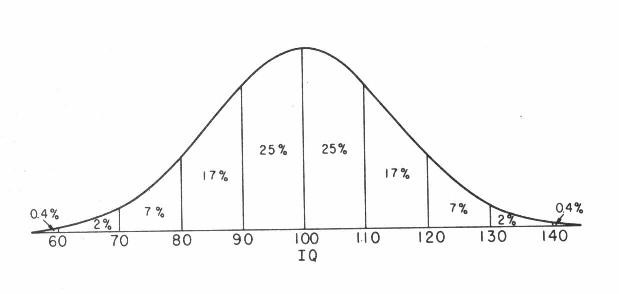
Pentru toţi ceilalţi, adică pentru marea masă a populaţiei şcolare, matematica este o constantă sursă de frustrare, de frică generatoare de ură şi mai ales o cauză a non-gândirii. Demarcaţia nu este de-a lungul unei linii clare; există desigur o zonă largă gri, a celor care înţeleg părţi din matematică, dar au şi parte de zone de neclaritate şi frustrare. Pentru cei aleşi de soartă matematica rămâne o amintire plăcută şi o activitate la care revin oricând cu bucurie după perioada şcolară. Pentru toţi ceilalţi viaţa de după matematica şcolară este doar o perioadă extinsă de convalescenţă psihică în care încearcă să-şi refacă cumva respectul şi încrederea de sine. În aceste condiţii orice reîntâlnire, cât de mică, cu matematica reprezintă o nouă zgârietură pe vechile răni cicatrizate ale sufletului.
Dacă faceţi parte, în oarecare măsură, din toţi ceilalţi, daţi-mi voie să vă spun că lucrurile nu au stat întotdeauna aşa în România. Permiteţi-mi să vă prezint pe scurt situaţia din punct de vedere istoric, o istorie, din păcate uitată şi neconsemnată.
Anii ’60-‘70
Analizând manualele şi culegerile româneşti din anii ’60 şi ’70, se simte clar cum matematica şcolară românească prezenta o formă deosebit de echilibrată între cele două direcţii principale: pe de-o parte preocuparea pentru formarea gândirii logice la marea masă a populaţiei şcolare, la corpul de bază al clopotului lui Gauss; pe de cealaltă parte, Gazeta matematică şi olimpiadele şcolare ofereau o foarte bună preocupare pentru excelenţă, adică pentru elevii din ramura din dreapta a clopotului lui Gauss. Din clasele gimnaziale, acolo unde se pun bazele sănătoase ale gândirii logico-matematice, merită amintite manualele lui Eugen Rusu şi ale lui A. Hollinger, dar şi culegerile lui Grigore Gheba şi ale lui Ivanca Olivotto, de care foarte multă lume îşi aduce aminte cu mare bucurie şi stimă. Şi la liceu atmosfera era la fel de sănătoasă. Selectarea numelor autorilor de la acest nivel ar fi şi mai grea; erau cu toţii autori care se formaseră în perioada interbelică şi care aduceau, alături de sănătoasa matematică tradiţională românească, tot ce era mai bun din matematica Europei de vest dar şi din matematică rusească, pe care o cunoscuserăm din plin în anii stalinizării forţate.
Pe lângă acestea trebuie amintite multele lucrări de metodică şi didactică traduse, atât din direcţia rusească, cât şi din Europa de vest şi de peste ocean. Aş aminti aici doar trei autori: rusul Boris Kordemsky şi americanul Martin Gardner în domeniul matematicii distractive, şi legendarul George Polya, maghiar naturalizat în SUA, cel mai mare didactician din lume în domeniul matematicii şcolare.
În paralel cu preocupările şi strădaniile metodico-didactice din acea perioadă, este obligatoriu să amintim aici două curente de preocupare “tangente” matematicii şcolare de masă, acestea fiind de o importanţă covârşitoare în înţelegerea situaţiei actuale.
Presiunea rigurozităţii ştiinţifice
În primul rând, trebuie evocată presiunea apărută din direcţia universitară pentru adaptarea matematicii predată în şcoli la cerinţele de rigurozitate pe care tot mai mulţi universitari le considerau absolut obligatorii. Astfel, acei ani au fost marcaţi de lupta dintre modernizatorii universitari, adepţi ai axiomatizării, a rigurozităţii teoretice şi a introducerii teoriei mulţimilor în matematica preuniversitară, pe de-o parte, şi tradiţionaliştii adepţi ai predării metodice şi didactice sănătoase, adaptată fiecărei vârste, folosind în gimnaziu predarea intuitivă formatoare de imaginaţie şi trecând treptat către o matematică mai riguroasă pănă la finalul liceului.
Să analizăm pe scurt istoricul situaţiei. După rezolvarea marii dileme a axiomei paralelelor prin Lobacevski şi Bolyai, sub binecuvântarea marelui Gauss, şi după epuizarea tuturor noilor posibilităţi deschise de acestea, concretizate sub titlul generos al Geometriilor neeuclidiene, după tumultuosul secol XIX deci, matematicienii s-au întors încă o dată la Geometria euclidiană. De data asta au făcut-o ordonat, axiomatic, extrem de riguros, cu lecţia învăţată de pe urma posibilităţilor năucitoare ce fuseseră găsite sub formă de fisuri între multele intuiţii şi evidenţe cu care era construită geometria clasică. Germanul David Hilbert a fost vârful de lance al grupului ce a acţionat la cumpăna dintre secole în acest sens. Lucrarea Bazele geometriei a lui Hilbert a influenţat mare parte din matematicienii care l-au urmat.
După primul război mondial se cristalizaseră în lumea matematicii două grupuri ale căror luări de cuvânt pot fi urmărite chiar şi în literatura tradusă la noi. Primul grup a fost acela al matematicienilor universitari de înaltă clasă care considerau că geometria riguros axiomatică trebuie să fie aşezată la baza matematicii şcolare, iar luările de cuvânt erau exrem de dure. Dau un singur exemplu: lucrarea publicată în 1927 la Londra Fundamentele geometriei euclidiene – H. G. Forder (Ed. Ştiinţifică, 1970).
Ca reacţie la “vociferările” primilor, s-a ridicat un al doilea grup care considera că matematica şcolară trebuie să-şi păstreze caracterul intuitiv, adaptarea pedagogică a fiecărei vârste şcolare fiind vitală pentru formarea gândirii matematice sănătoase.
Curentul reformator universitar a prins, de pildă, foarte puternic în Franţa anilor ’50 –’60. Ţinând cont de faptul că România comunistă şi-a redeschis în anii ’60 legăturile cu Franţa condusă de un guvern socialist, mare parte din zbuciumul reformelor matematice franceze curgea şi înspre noi. Astfel, anii ’60-’70 au fost martorii unor lupte tot mai active între reprezentanţii celor două grupuri din ţara noastră. Cele mai clare luări de cuvânt ale grupului ce apăra valorile pedagogice la noi îi aparţin lui Eugen Rusu în Psihologia activităţii matematice (Ed. Ştiinţifică, 1969) şi în Problematizare şi probleme în matematica şcolară (Ed. Did. şi pedagogică, 1978).
Olimpiada de matematică
Din punct de vedere al matematicii şcolare de excelenţă trebuie totodată precizat că în 1959 România organiza prima ediţie a Olimpiadei internaţionale de matematică. Tot în România a fost organizată şi a doua ediţie. Următoarele ţări organizatoare au fost Ungaria în 1961, Cehoslovacia în 1962, Polonia în 1963, U.R.S.S. în 1964, R.D.G. în 1965, Bulgaria în 1966, Iugoslavia în 1967, a zecea ediţie iar în U.R.S.S. în 1968, din nou în România în 1969, Ungaria în 1970, Cehoslovacia în 1971, Polonia în 1972, U.R.S.S. în 1973, R.D.G. în 1974, Bulgaria în 1975.
La primele patru ediţii au participat elevi din Bulgaria, Cehoslovacia, Republica Democrată a Germaniei, Polonia, România, Ungaria, U.R.S.S. şi Vietnam. Apoi au mai apărut Iugoslavia şi Mongolia, şi o participare ciudată la a şaptea ediţie a Finlandei. Cu excepţia amintită, la primele opt ediţii au participat doar ţări din blocul comunist. Pentru cine nu a înţeles, merită totuşi accentuat: Olimpiada internaţională de matematică este o invenţie românească şi primele opt ediţii au fost de fapt o afacere internă a blocului comunist. De-abia a XVIII-a ediţie a fost organizată de o ţară necomunistă (Austria în 1976). Primele ţări capitaliste participante au fost Anglia, Franţa, Italia şi Suedia la ediţia din 1967 organizată de Iugoslavia. Statele Unite ale Americii s-au înscris prima dată în 1974.
La primele două ediţii locul întâi a fost obţinut de elevi din România, Cehoslovacia şi Ungaria. De la a treia ediţie ţara noastră s-a mai găsit sporadic între fruntaşi, la ediţiile V, VIII, IX, X, XIV, XVI, XX (date extrase din lucrarea Olimpiadele Internaţionale de Matematică – E. A.Morozova, I. S. Petrakov, V. A. Skvorţov, Ed. Tehnică, 1978).
La sfârşitul anilor ’70 bătălia de la olimpiadele internaţionale de matematică se dădea între ruşi şi americani, ajungând, la fel ca în olimpiadele sportive, la nivelul războiului rece. Era evident că România pierduse de mult supremaţia în domeniu. Conducerea de Partid şi de Stat dorea cu orice preţ din nou rezultate constante la vârful olimpiadelor internaţionale de matematică. Trebuia făcut ceva! Astfel, la indicaţiile venite de sus de tot, s-a hotărât creşterea nivelului matematicii din şcolile noastre. Iar asta s-a văzut dureros în schimbările pornite la finalul anilor ’70.
Reforma “din 1980”
Acesta a fost momentul când “olimpiştii” s-au aliat cu “modernişti universitari” preluând puterea în matematica şcolară românească. Aceştia şi-au împărţit pur şi simplu în mod prietenesc timpul orelor de matematică, dând încet la o parte tradiţia de predare naturală şi sănătoasă prin problematizare pe care o stăpâneau majoritatea profesorilor. Iar asta se întâmpla cu binecuvântarea conducerii din vremea respectivă, ce era avidă de noi premii cu care să poată demonstra superioritatea orânduirii socialiste, mai ales a modelului socialismului românesc al lui Ceauşescu.
Saltul de dificultate teoretică şi al problemelor se poate verifica de către oricine pe noile manualele apărute în acei ani. Unii autori au fost mai zeloşi, alţii s-au străduit să găsească o linie de compromis. Nu s-au schimbat doar manualele, ci şi modul de abordare a lecţiilor. Tratarea axiomatică a materiei a făcut ravagii în matematică. La examenele profesorilor (definitivat, gradul II, etc.) se dădeau obsesiv elemente din introducerea axiomatică a geometriei. Autorităţile nu au mai fost interesate dacă profesorii ştiu să predea o lecţie astfel încât elevii să o înţeleagă, ci dacă profesorii o stăpânesc din punct de vedere axiomatic şi o predau teoretic ca atare. Predarea de până atunci, specifică şi adaptată în decurs de zeci de ani fiecărei vârste şcolare, era înlocuită cu o predarea de sorginte academică. Dacă până în anii ’70 profesorul creea lecţia împreună cu elevii, existănd la oră un permanent dialog şi o reglare a nivelului lecţiei, în noua predare profesorul trebuia pur şi simplu să turuie lecţia căt mai riguros, ca la carte, chiar dacă simţea că elevii nu înţeleg elementele prezentate.
Această reformă a lovit în toate clasele, dar cu precădere în gimnaziu. Mai ales în clasele V-VI schimbările au fost resimţite cel mai greu de către elevi, pentru că la această vârstă majoritatea elevilor pur şi simplu nu sunt dezvoltaţi pentru a primi matematică pentru elevi mari. Piaget explică foarte clar: gândirea copiilor, numită stadiul operaţional concret, este activă la copii până la 11-12 ani. Gândirea adultă, adică stadiul operaţional formal se generalizează pe la 12-13 ani. Or, această reformă i-a confruntat pe elevii de-a V-a cu o aritmetică tratată algebric şi pe cei de clasa a VI-a cu o geometrie excesiv de riguroasă, de inspiraţie axiomatică, abstractizarea lovindu-i pe elevi din plin. Ideea ghidantă a fost ca elevii să fie forţaţi a trece în stadiul de gândire adultă cât mai repede. De-abia la programa din 2009 s-au făcut ceva paşi timizi de corectare a unor elemente introduse în 1980 în clasa a V-a, dar şi azi sunt încă profesori, chiar autori de culegeri, care nu înţeleg sensul acestora.
În anii ’80 profesorii erau bulversaţi şi nu înţelegeau cum să predea noile inepţii din manuale. Încet însă, de-a lungul anilor, cei mai mulţi profesori au fost disciplinaţi şi aduşi pe noua linie de predare. Iar în 1990, la zece ani de la această reformă, deja toată lumea era gata îndoctrinată, mândră de olimpicii noştri şi de cât suntem noi de tari la matematică. Astfel, după Revoluţie nimeni nu se mai gândea la abandonarea acestui sistem, care hrănea puternic orgoliul naţional.
Eliberarea de comunism?
În ceea ce priveşte problemele parcurse la clasă sau date ca temă, nivelul şi diversitatea acestora a urmat în continuare o pantă ascendentă, crescând de la un an la altul. Iar când nu se mai putea suporta presiunea apărută din cauza problemelor tot mai grele dintr-o lecţie, această lecţie se scotea pur şi simplu din programă, desfiinţând-o cu totul. A se vedea de pildă eliminarea patrulaterelor inscriptibile din clasa a VII-a după boom-ul de probleme pe această temă. În general, fenomenul de alunecare a materiei din facultate în liceu, din liceu în gimnaziu, din gimnaziu în ciclul primar şi desigur din primar în grădiniţă a reprezentat o constantă a şcolii noastre după 1980.
În 1997 treaba încă mergea minunat; copiii încă nu erau distruşi de stat toată ziua la televizor şi la calculator. Ca urmare a avut loc un nou salt în dificultate prin reformarea programei înspre mai greu şi prin introducerea manualelor alternative. Autorii acestora au scos aproape de tot exerciţiile şi problemele uşoare, de învăţare, din oferta de lucru. În schimb, am simţit ca şi cum toată tradiţia olimpiadelor a fost descărcată în aceste noi manuale. Tot sistemul şcolar matematic vorbea numai despre olimpiade şi centre de excelenţă, şi nimeni nu se mai gândea la toţi ceilalţi care, uitaţi fiind de sistem, au luat-o tot mai clar pe panta suferinţei accentuate din cauza matematicii.
Tot în manualele alternative au început să apară şi primele gafe dure din punct de vedere a corectitudinii matematice. De exemplu, atunci a apărut ideea de definire a ariei triunghiului. Însă oricine ştie că aria triunghiului este jumătate din aria unui paralelogram, iar aria acestuia se deduce uşor din aria unui dreptunghi.
Au urmat ani de mutare haotică a lecţiilor sau capitolelor în jos sau în sus, încât acum nimeni nu mai ştie clar care este logica lucrurilor. Preşedintele Iohannis a făcut aluzie de curând la această stare de continuă reformă, atenţionând: reformă, nu reformită. Iar urmarea acestor reforme în cascadă se vede la clasă, la toate nivelele: elevii primesc o matematică de multe ori fără nici un sens, fără nici o logică, ce trebuie pur şi simplu tocită, contrar oricărui sens şi bun-simţ matematic.
Iată câteva exemple concrete de îngreunare a limbajului matematic, urmare a reformei lui Ceauşescu din 1980. Să ne amintim de pildă cât de greu s-au dezobişnuit profesorii de unghiul plan corespunzător diedrului dintre planele…. De-abia după 2000 a început să fie acceptat unghiul diedru dintre planele…, şi exemplele în acest sens pot continua la nesfârşit. Oare cum de am priceput şi iubit geometria noi, cei care am învăţat înainte de 1980 din manualele profesorului Hollinger, atunci când scriam ∢A = 60˚ în loc de mult mai riguroasa scriere m(∢A) = 60˚? Noi nu am învăţat despre congruenţă, dar am înţeles geometria. La noi intersecţa a două drepte, de exemplu a diagonalelor unui trapez, se scria AC ∩ BD = O, pe când ca profesor, după 1990, nu aveam voie să scriu decât varianta AC ∩ BD = {O} corectă prin prisma teoriei mulţimilor. La copil nu se mai gândea nimeni, la faptul că el nu gândeşte prin prisma teoriei mulţimilor, ci el ştie că intersecţia a două drepte este un punct. Şi acum copiii sunt bulversaţi de scrierea divizibilităţii în forma universitară 3|12 în loc forma naturală 12⋮3.
Practic, la reforma din 1980 matematica a fost îngreunată pe două direcţii de bază: o teoretizare riguroasă excesivă în predare şi o creştere clară a dificultăţii problemelor. Ambele procese au continuat panta ascendentă până către anul 2000 şi chiar mai încoace, ducând la o inaccesibilizare extremă a matematicii şcolare. Cu cât nivelul creştea mai tare, cu atât aveam tot mai puţin elevi care puteau face faţă matematicii şcolare. O a treia direcţie de schimbare, cea metodico-didactică, a apărut în acest proces de îngreunare doar ca o consecinţă a introducerii primelor două: predarea naturală practicată înainte de 1980 era prea mare consumatoare de timp din ora de 50 de minute. Aceasta a trebuit să se retragă pentru a face loc marii teoretizări şi tot mai dificilelor şi bogatelor aplicaţii. Astfel, actualmente avem o matematică şcolară adresată şi aplicabilă unui procentaj din populaţia şcolară care evoluează, de la o temă la alta, undeva între 1% şi 10% din populaţia şcolară la nivel naţional. Iar asta dovedeşte o stare de inconştienţă şi iresponsabilitate crasă. Procentul de asimilare a materiei este apoi ridicat în anii de final de ciclu prin munca de recuperare a profesorilor de la clasă şi prin orele particulare plătite de părinţi.
Faptul că actualmente nimeni nu mai ştie de reforma din 1980 şi de liniile acesteia, explică de ce lumea matematicii şcolare româneşti bâjbâie în continuare într-o ceaţă totală şi nu ştie încotro să o apuce. Profesorii sunt blocaţi în paradigma acelei reforme şi nimeni nu ştie cum să iasă din această situaţie. Mai rău: nimeni nu ştie nici măcar că ar trebui să iasă din această paradigmă. În celălalt colţ al clasei (al ringului?), majoritatea elevilor suferă fiecare în felul lui. Părinţii, societatea, nu mai ştiu ce să facă cu repulsia odraslelor faţă de matematică, iar de pe băncile şcolilor pleacă în fiecare an tot mai puţini absolvenţi care înţeleg şi iubesc cu adevărat matematica.
Iar asta este o dramă! Este drama supremă a matematicii noastre şcolare.
Anexă de final
În data de 12 feb. 2016 am trimis D-lui Academician Solomon Marcus un e-mail cu materialul istoric complet din Reforma uitată (vezi articolul de 20 pagini cu toate detaliile: Istoria unei reforme uitate a matematicii şcolare româneşti, partea I, postat pe pentagonia.ro). În data de 13 feb. 2016 am primit de la dânsul următorul răspuns:
Drag Profesor Grigorovici,
Foarte interesnta povestea Dv, care-mi e si mie foarte cunoscuta. Am citit un prim fragment si voi continua lectura. Ramanem in legatura, voi reveni.
Cu drag,
Solomon Marcus
Acesta a fost primul şi ultimul e-mail primit de la Dl. Solomon Marcus; din păcate nu a mai revenit. Peste o lună, în 17 martie, dânsul a plecat cu totul din această lume şi ne-a lăsat să luptăm aici mai departe. Îmi place să cred că a plecat dintre noi cu încrederea că vom reuşi totuşi să îndreptăm în curând lucrurile în matematica şcolară românească.
8 mai 2016
Prof. Constantin Titus Grigorovici
8 bile – Matematică distractivă în G.M.
De curând am căutat într-o cutie cu cărţi vechi şi am dat peste două caiete de Gazeta Matematică vechi. Într-una dintre ele (GM&F seria B, ianuarie 1958) am găsit următoarea problemă (E:1075, pag 49) clasificabilă uşor drept problemă de matematică distractivă (am modificat textul pentru elevii de azi):
Avem opt bile identice ca mărime, culoare şi textură; ştim că toate sunt la fel de grele cu excepţia uneia care este un pic mai grea (diferenţă insesizabilă la comparaţia în mână). Explicaţi cum putem stabili care este bila mai grea efectuând doar două cântăriri cu o balanţă.
Daţi problema aceasta la orice clasă şi bucuraţi-vă alături de elevi de ea. Ca adulţi, vă puteţi gândi şi de ce autorul (nesemnat) a dat 8 şi nu 9 bile.
O problemă din Suedia
În urmă cu doi ani, am primit de la Kjell Samuelsson de lângă Stokholm următoarea întrebare, din categoria matematică distractivă (distractivă, dar nu neserioasă).
Ce număr urmează?
61, 71, 101, 131, 151, …?
Iar, dacă tot am vorbit de dl. Kjell Samuelsson, dânsul a împlinit primăvara asta 100 de ani (număraţi în baza 8). La mulţi ani! dragă Kjell.
Matematică de pe facebook: 5 sau 120?
Pe Facebook e cam ca la balamuc (sau ar trebui să scriu balamook?); postează fiecare ce-i trece prin cap şi mulţi o dau mai departe, poate ştie cineva să rezolve minunea. O elevă mi-a atras atenţia asupra acestei “probleme”, mai degrabă o farsă pentru foarte mulţi (mai ales dintre aceia care n-au apucat să ajungă prin clasa a X-a sau au uitat c-au fost pe-acolo). Problema este plină de “bombe fumigene”, care să-ţi distragă atenţia în procesul de rezolvare, fiind un exemplu minunat despre cum o banalitate poate fi îmbrăcată într-o problemă. Din acest punct de vedere, rezultatul acestei strădanii este chiar foarte reuşit. Soţia mea spunea că, atunci când vin elevii cu o ciudăţenie din asta, refuză să se implice până nu vede cu ochii ei problema acolo de unde a fost luată, elevii nefiind întotdeauna atenţi la toate detaliile (citită de pe ecranul unui smartphone înghesuit este şi mai uşor să ratezi detalii minore, dar esenţiale). Deci, iată “problema”:
25 – 55 +(85 +65)
Poate n-o să vă vină să credeţi, dar rezultatul este într-adevăr 5!
Finalul Geometriei în clasa a VIII-a (5)
Geometria sferei în sprijinul geografiei; Corpuri de rotaţie
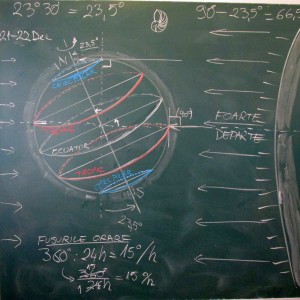
După parcurgerea lecţiei despre sferă mi-am permis ora următoare un “20 minute” de studiu al unor elemente de geografie şi astronomie legate de geometria sferei. Elevii le cunosc teoretic, dar din păcate cunoştinţele de geometrie ale profesorilor de geografie nu acoperă întotdeauna toate fineţurile de gândire ale fenomenului, astfel încât de multe ori aceste cunoştinţe ajung să fie doar învăţate pe de rost, fără a fi şi înţelese. Şi în nici un caz profesorul de geografie nu va merge la clasă cu compasul şi cu raportorul pentru a face un desen cât mai corect pe tablă.
În a doua parte a orei am oferit elevilor nişte probleme cu corpuri de rotaţie. Acestea nu mai sunt în programă cam de un sfert de secol, dar eu consider că sunt foarte clare, conţinând o matematică vie, plină de gândire accesibilă elevilor de a VIII-a şi care chiar le aduce bucurie prin satisfacţia rezolvării, acestea nefiind prea banale. Măcar aceste trei probleme ar trebui să le parcurgă orice elev, dar se mai pot face şi altele. Pe tablă găsiţi doar problemele; rezolvările sunt la elevi în caiete :-).
Titus Grigorovici
Finalul Geometriei în clasa a VIII-a (4)
Sfera şi bila
Lecţia despre sferă/bilă cu aria şi volumul acestora conţine demonstraţii legendare, ce pot oferi o mare satisfacţie elevilor buni de clasa a VIII-a. Nu mi-am propus pentru această postare să prezint în detaliu toată lecţia, dar mă gândesc să va descriu puţin cele două poveşti cu care pregătesc calcului volumului, respectiv al ariei, înainte de a vă lăsa să vedeţi lecţia de pe tablă.
Pentru volum – ciudat, dar se începe cu demonstrarea formulei volumului – se construieşte un corp interesant, un cilindru cu secţiunea axială pătrată, de aceeaşi rază cu sfera, din care se scot două conuride la cele două baze, conurile având vârful comun în “centrul” cilindrului. Eu le descriu elevilor acest corp, comparându-l cu o conservă de pateu căreia i-am scos ambele capace şi din care am extras cele două conuri de pateu cu un cuţit cu vârf. Ideea este de a arăta că volumul pateului rămas este egal cu volumul bilei, arătând aceasta prin faptul că la orice înălţime secţionăm cele două corpuri, ariile secţiunilor vor fi egale. Partea de calcul a demonstraţiei este simplă şi percutantă: nici nu-ţi dai seama bine cum ai pornit şi este deja gata.
Pentru demonstrarea formulei de arie le povestesc elevilor despre un vânzător de pepeni care are un pepene perfect sferic şi un cuţit cu care taie bucăţi de degustat. Cuţitul are lama de lungime exact cât raza pepenelui iar bucata oferită spre degustare, cu vârful exact în centru, are forma unei piramide cu baza de coajă (puţin bombată). Apoi ne imaginăm că acest vânzător de pepeni îşi propune să tot taie bicăţi pentru degustare cât mai înguste (pentru a evita baze bombate), deci cât mai multe, şi le aranjează pe masă, toate cu vârful în sus şi aşa mai departe. De aici încolo fiecare se poate descurca cu povestea şi cu trecerea acesteia în demonstraţie şi în calculul pentru obţinerea formulei.
După ce avem formulele fac câteva exerciţii mai mult orale de calcul a ariei şi a volumului unei semibile şi a unui sfert de bilă (merge uşor şi optimea de bilă). Spor la lecţie de pe tablă.
Titus Grigorovici
Matematică distractivă pe SCAM SCHOOL
Un elev de clasa a VIII-a m-a atenţionat de curând asupra acestei emisiuni, găsită pe net. Am căutat scamschool, am intrat pe Scam School / Test Tube şi am găsit (printre multe alte nebunii) câteva probleme foarte drăguţe de matematică distractivă (mathematical puzzles). Emisiunea este prezentată într-un mod foarte atractiv/agitat de către Brian Brushwood şi la majoritatea episoadelor este vorba de un pariu, anume cine plăteşte berea.
Totuşi, cred că mai există şi un alt motiv – în afară de berea din timpul emisiunii – pentru care partenerii de discuţie ai lui Brian sunt de peste 20 ani, chiar şi până în 40. Oare care ar fi acest motiv? Pentru că problemele sunt tehnic, prin prisma rezolvărilor, la nivel de gimnaziu (în general de clasa a 5-a). Haideţi să vedem câteva dintre aceste probleme (am căutat din emisiunile ultimului an). Interesant este că unele dintre ele permit mai multe soluţii. Le prezint pe fiecare cu titlul original al episodului respectiv:
The Most Powerful Number Puzzle. Se dau toate cifrele 0 1 2 3 4 5 6 7 8 9 = 1. Aveţi voie să puneţi orice semne sau operaţii din matematică, dar să păstraţi ordinea cifrelor (de la stânga la dreapta), şi trebuie să obţineţi rezultatul 1. Se caută desigur cea mai elegantă soluţie.
Fill in the Blanks: A Number Puzzle. Trebuie scrise trei numere a căror sumă să dea 30, adică ___ + ___ + ___ = 30 folosind ca piese de lucru doar unele din următoarele numere: 1, 3, 5, 7, 9, 11, 13, 15. La acesta Brian a trebuit să plătească el berea, pentru că prietenii lui au găsit o altă soluţie decât a sa, dar la fel de frumoasă. Un elev din a VII-a a găsit la prima prezentare, în 3-4 minute, altă soluţie decât cele două din emisiune.
The Toothpick Variable. Această problemă cu scobitori cere să stabiliţi egalitatea mutând doar o singură scobitoare în membrul stâng, pentru a obţine într-adevăr numărul patru (în membrul drept este 4 pe sistemul roman vechi: IIII, nu IV):
CRUSH Smug Geniuses With The Simplest Number Puzzle. În această problemă se primesc câteva bileţele pe care trebuie să le ordonaţi pentru a obţine rezultatul 24 (bileţelele =, 2 şi 4 sunt fixe). Atenţie că şi aici am găsit mai multe soluţii (daţi problema la elevi într-o pauză şi veţi vedea ce iese).
Single Digit FACE-OFF. Se cere ca folosind un calculator de buzunar să obţineţi numărul 17 apăsând doar cifra 5 şi orice/oricâte operaţii doriţi. Desigur că sunt căutate soluţii cât mai frumoase, adică cu cât mai puţine folosiri ale tastei 5. În filmuleţ apar soluţii cu şapte de 5, cu şase de 5, cu cinci de 5, chiar şi cu patru de 5, dar cireaşa de pe tort este o variantă în care se apasă tasta 5 o singură dată, iar în rest doar taste de operaţii.
Match Math. Un ultim exemplu este cu chibrite (chibrite, scobitori, ce gasiţi). Scrieţi cu chibrite “egalitatea” VII = I. Sarcina este să mutaţi un chibrit în partea stângă a semnului egal pentru a obţine într-adevăr rezultatul 1.
Morala poveştii: Pe vremuri, Martin Gardner publica în Scientific American probleme de matematică distractivă, câte una pe revistă. Răspunsul apărea de-abia în următorul număr al revistei. Această politică îţi lăsa chiar timp ca să te gândeşti şi să cauţi tu o soluţie. Ori, în emisiunile de pe Scam School totul decurge foarte repede şi, în avântul emisiunii, primeşti şi răspunsul în 2-3 minute. Astfel eşti redus la un simplu spectator la SPECTACOLUL GÂNDIRII.
Eu consider că rolul nostru ca profesori de matematică este să-i atragem pe elevi să fie activi în acest proces al gândirii, nu să se uite pasiv, din exterior, la cineva care gândeşte. Astfel, eu le dau elevilor problemuţe din acestea şi îi las să gândească (câteva minute, sau rămâne ca temă). Şi, în general, chiar careva reuşeşte de obicei să găsească o soluţie valabilă. Cât despre numele site-ului respectiv, nu l-am dat la clase ca să nu se uite şi să găsească acolo răspunsurile, rămânând să gestionez eu situaţia, când şi cum le dau răspunsul.
Constantin Titus Grigorovici
Finalul Geometriei în clasa a VIII-a (3)
Conul circular drept
Sărim peste lecţia despre cilindrul circular drept, pentru că aceasta este una din cele mai simple lecţii de clasa a VIII-a. Plecând de la premiză că profesorul chiar se străduieşte, el va reuşi o lecţie foarte bună, elevii implicându-se şi putând ajuta cu adevărat. Toţi au văzut până acum conserve, chiar au desprins eticheta de pe o butelie de Cola, aşa că vor înţelege foarte bine aria laterală (eu chiar desenez desfăşurarea suprafeţei laterale sub formă de dreptunghi care “se mai ţine un pic de cilindrul desenat”). La volum, principiul “aria bazei înmulţit cu înălţimea” se poate discuta foarte bine pe baza pachetelor de biscuiţi rotunzi: Câtă cantitate este în pachet? Păi, cântăresc un biscuite şi număr câţi biscuiţi sunt în pachet.
Mai deosebită este lecţia următoare, despre conul circular drept. Volumul acestuia nu generează mari probleme; elevii înţeleg analogia cu volumul piramidei. Foarte interesantă este însă, şi merită lucrată cu răbdare, deducerea formulei pentru aria laterală a conului. Eu predau elevilor exact lecţia pe care am primit-o în clasa a VIII-a de la profesorul meu Wilhelm Schoch, lecţie ce m-a impresionat profund şi cu ajutorul căreia am putut oricând să-mi re-deduc formula în cap.
De fiecare dată când predau această lecţie cu împărţirea sectorului de cerc în foarte multe “triunghiuri tare înguste” nutresc speranţa că sădesc în mintea elevilor o sămânţă pentru o evoluţie frumoasă în liceu la calcului diferenţial şi integral.
O tehnică similară se foloseşte şi la găsirea formulei pentru aria laterală a trunchiului de con circular drept, doar că suprafaţa laterală desfăşurată (un sector de inel circular) se descompune într-o sumă de “trapeze” foarte înguste. Calculul merge similar şi, fiind la a doua întâlnire, le place foarte mult elevilor.
Iată în continuare pozele tablei de la lecţia despre conul circular drept.
Titus Grigorovici