Elevul de gimnaziu este confruntat constant cu elemente de matematică peste nivelul său de asimilare, peste capacităţile sale de înţelegere. Procesul a început în urmă cu decenii, la început fiind luat ca reper şi ca justificare nivelul celor mai buni elevi. O altă cauză este faptul că au fost coborâte în clasele gimnaziale lecţiile în forma în care acestea se parcurgeau la o a doua trecere, una mai elevată, doar în liceu. La ora actuală, în multe cărţi şi la mulţi profesori avem o atitudine de felul: De ce să le-o dăm în gimnaziu doar intuitiv, pe cazuri particulare, ca s-o şi înţeleagă cât mai mulţi? Hai să le-o dăm direct în forma generală, de matematică matură. Nu-i bai că cei mai mulţi nu vor mai înţelege nimic. Important este că noi arătăm “lumii întregi” că stăpânim forma cea mai înaltă din punct de vedere a exprimării riguroase matematice. Pentru că există desigur întordeauna riscul ca să ne apostrofeze careva de felul “cum, nu şti forma generală, cea de vârf?” (de curând am vorbit despre aceste aspecte urâte ale interacţiunii din lumea profesorilor de matematică).
Desigur că fenomenul se petrece şi în cadrul claselor gimnaziale, adică între acestea, ca anumite elemente să fie predate în clase mai mici, deşi elevii nu au capacitatea sau cunoştinţele necesare a le pricepe decât mai târziu, după ce au învăţat elemente suplimentare. Profesorii, care însă cunosc toată materia, au în astfel de momente dificultăţi reale de a nu “turna toată tema respectivă” peste elevi în lecţia predată într-o clasă mică. În această miniserie mi-am propus să abordez trei astfel de exemple în care diferite elemente matematice sunt predate în forme prea elevate pentru o primă abordare.
Care este rezultatul unor astfel de predări? Elevii nu înţeleg mai nimic (cel puţin marea masă a elevilor), se stresează (în toate formele ce se pot imagina, iar psihologii pot descrie multe) şi se îndepărtează de matematică. În funcţie de posibilităţi părinţii reacţionează angajând un meditator. Mulţi dintre aceştia, la rândul lor, fentează parcurgând cu elevii lecţiile în avans, între patru ochi existând şanse mai mari ca elevul să priceapă totuşi ceva, mai ales dacă o faci înainte de a fi intervenit sperietura de la clasă.
O altă urmare este faptul că cei mai mulţi elevi reduc matematica la un set de reguli şi de texte ce trebuie pur şi simplu învăţate pe de rost, gândirea fiind eliminată cu totul din discuţie (din procesul matematic). Dramatic este faptul că elevii nici măcar nu înţeleg că ei nu gândesc. Astfel, ei ajung să confunde înţelegerea adevărată, gândită, cu impresia că pot să redea ceva (total sau într-o oarecare măsură): dacă pot reda o situaţie înseamnă că au înţeles. Asta nu este însă de obicei adevărat: imediat ce schimbi puţin (sau mai mult) modelul, vei vedea o bulversare generală, manifestările mergând de la blocaj total până la situaţii în care vei primi rezolvări total anapoda (de pildă, demonstraţie cu metoda triunghiurilor congruente la probleme unde nici măcar nu apar în figură triunghiuri congruente).
*
Să abordăm deci primul exemplu propus, anume includerea cuvântului “coplanare” în definirea dreptelor paralele din prima parte a clasei a 6-a (unii profesori se “pot trezi” să o dea chiar şi în a 5-a): Două drepte coplanare care nu au puncte comune se numesc paralele (sau orice altă variantă pe care o preferaţi, de pildă cu folosirea cuvântului “neintersectate” etc.).
Să ne punem în locul elevilor. În faţa lor se deschid două căi: fie înţeleg lucrurile şi atunci le pot reda, eventual cu cuvintele lor, dar oricum le pot desigur folosi la nevoie, fie nu le înţeleg, iar atunci apare impulsul de a le învăţa pe de rost (impuls personal sau la sugestia părinţilor). Incluzând în această definiţie un cuvânt pe care elevii nu-l înţeleg, asta duce la obturarea căii de înţelegere a noţiunii, apare sperietura şi blocajul şi rămâne ca soluţie disperată doar învăţarea pe de rost. În acest caz însă, la cei mai mulţi elevi memoria nu poate duce pe durată stăpânirea definiţiei, fără să mai discutăm că nici măcar nu putem spera la apariţia cu timpul a înţelegerii noţiunii, pentru că mentalul a fost blocat de sperietura iniţială.
Aşa se ajunge la starea de toceală împănată cu multe spaime în matematică. Rezultatul este că o noţiune elementară, destul de accesibilă în principiu, devine un “balaur” pe psihicul copilului. Apoi, cuvântul fiind relativ lung şi având deja ataşată sperietura, starea de frică se extinde şi la alte situaţii, de pildă la noţiunea de drepte perpendiculare (tot un cuvânt lung şi începând cu litera p).
Desigur că, din punct de vedere al rigurozităţii exprimării matematice, cuvântul “coplanare” nu poate fi omis, pentru că asta ar lăsa “portiţa deschisă” pentru posibilitatea ca “cineva” să înţeleagă şi posibilitatea acelei poziţionări denumită în clasa a 8-a drept “necoplanare”. Să analizăm puţin aspectele acestui moment.
Păi, în primul rând, putem susţine liniştit că marea majoritate a elevilor nu vor “vedea” situaţia dreptelor necoplanare, mai ales dacă profesorul desenează imediat măcar o reprezentare a două drepte paralele (renumitul efect de “în figura alăturată” care îi direcţionează elevului înţelegerea). Totuşi, există în continuare riscul ca un “mic Einstein” să “scoată porumbelul pe gură”, respectiv să ia profesorul la întrebări, că “şi dacă le pune aşa:…?” arătând sau sugerând cumva situaţia dreptelor necoplanare (de pildă cu două creioane în aer).
Acest lucru se poate intâmpla din două cauze: fie acelui elev chiar “i-a mers mintea” singur, adică a văzut în propria imaginaţie poziţia unor drepte necoplanare (neintersectate dar nici paralele), fie elevul are informaţia respectivă primită deja de undeva. În primul rând, eu consider ca extrem de rară prima situaţie, acea când elevul “vede singur” poziţia respectivă (nu imposibilă, dar foarte puţin probabilă).
Revenim aşadar la faptul că unii copii află lucrurile mai devreme decât din lecţia de la şcoală. Am povestit despre situaţia când un meditator particular parcurge lecţiile în avans (un fenomen foarte urât, ce se întâlneşte pe scară tot mai largă în oraşele româneşti). Desigur că sunt probabili şi părinţi care au ajuns la concluzia că trebuie ei însuşi să facă aşa ceva. Există şi elevi care ajung la concluzia că e bine dacă fac aşa ceva: au mult mai mult succes la ora următoare dacă citesc în avans lecţia din manual, iar cu timpul acest model le devine felul lor de a fi. Desigur că nimeni nu se gândeşte care este efectul unei astfel de acţiuni asupra celorlalţi elevi sau asupra mersului lecţiei în general.
Există şi o altă cale prin care diverse cunoştinţe pot ajunge ca informaţii la copii, anume prin diferite cărţi cumpărate de către părinţi sau diverse rude/ prieteni, date copiilor doar aşa, “să-i trezească curiozitatea”. Copiii le parcurg mai mult sau mai puţin superficial, dar oricum rămân cu cuvinte sau cu imagini şi pe baza cărora intervin în lecţii ulterioare (dacă îşi amintesc). Există diverse astfel de cărţi, inclusiv unele cu o parcurgere destul de superficială, gen “enciclopedie în imagini” traduse din alte limbi. Acestea alimentează şi ele respectivul fenomen de “care pe care”, fenomen de dat mare pe baza a care ştie mai multe şi mai repede. Desigur că nici internetul nu poate fi exclus din această discuţie, deşi nu i-aş acorda o pondere prea ridicată.
Să revenim totuşi la cuvântul nostru buclucaş. Cuvântul coplanar este un termen tehnic ce ţine de clasa a 8-a, respectiv de geometria în spaţiu; acelaşi lucru este valabil şi în legătură cu cuvântul necoplanar. Înţelegerea cuvântului coplanar are loc atunci când este privit din afară (din afara unui plan), adică atunci când persoana care-l foloseşte se poziţionează “mai sus”, adică “la un nivel superior”, în cazul acesta la nivel 3D, din care ne uităm la o parte a “lumii în care suntem” – asta putem să facem uşor – şi îi analizăm “un obiect”, o zonă etc.
Dimpotrivă, în clasa a 6-a copilul este mental “în plan”, adică în geometria 2D, specifică unei poze, aşa încât el nu este în stare să facă acest “flip-flop”, această tumbă imaginară, de a se ridica în 3D (într-o “altă dimensiune”), pentru a analiza situaţia, iar apoi de a coborî din nou în starea mentală de 2D. Acest lucru este valabil mai ales dacă nu se face nici cea mai mică pregătire în acest sens.
Mai există însă şi un alt aspect – deloc neglijabil, anume acela al autoperceperii profesorului de matematică. Noi, ca matematicieni, nu acceptăm să vorbim folosind aspecte false, neadevăruri. Aşa este fiinţa noastră de matematicieni. Aşa suntem noi. Ca urmare, simpla eliminare a acestui cuvânt nu ar rezolva problema. Ne-ar “zgâria pe creier” pe mulţi dintre noi. Poate că unul sau altul dintre profesori l-ar putea elimina din propria exprimare, din predare (doar aşa, pentru că a înţeles ce perturbare produce acest cuvânt la nivelul majorităţii elevilor), dar sigur nu le poţi cere tuturor acest gest. La nivel naţional soluţia respectivă sigur nu este una viabilă.
Aşadar, ce-i de făcut? De obicei, atunci când ridic o problemă încerc să vin şi cu o soluţie. În speţa de faţă mă tot băteau gânduri de genul: “pe vremea mea”, adică înainte de 1980, în manualele lui Hollinger adică, n-am avut aşa ceva. Mă mulţumeam cu atâta: bodogăneam şi gata. Pănă când mi-am făcut prin vacanţa de iarnă timp şi am scos cutia cu manualele vechi din copilărie. Surpriza a fost destul de puternică: şi Hollinger prezenta situaţia corect şi complet, excluzând neînţelegerea, dar o făcea într-un limbaj “pe mintea copilului”. Iată cum sună definiţia din manualele copilăriei mele:
Definiţie: Două drepte din acelaşi plan care nu au nici un punct comun se numesc drepte paralele (A. Hollinger, Geometrie, Manual pentru clasa a VI-a, Editura didactică şi pedagogică, 1977). Pentru înţelegera întregului “tablou” redau în continuare în citat şi următorul rând legat de acest subiect:
Pentru prescurtare, se foloseşte semnul ; de exemplu: AB CD sau CD AB (fig. IV.1). Întrerup citatul, precizând că aici, în manual, urmează o figură cu două drepte paralele (“orizontale”; eu aş fi pus şi unele “oblice”; în lecţia de la tablă eu pun întotdeauna trei situaţii: o pereche de drepte “orizontale”, o pereche “verticale” şi una cu drepte “oblice” paralele). Reiau citarea din manualul lui Hollinger:
În definiţia dreptelor paralele trebuie spus că dreptele sînt în acelaşi plan. Dreptele d şi d’ din figura IV.2 (două muchii ale unui cub) n-au nici un punct comun, totuşi ele nu sînt paralele, căci nu sînt în acelaşi plan. (…)
Întrerup din nou citarea textului, făcând o paranteză logică, anume cu precizarea că în continuare autorul se ocupă şi de situaţia ciudată când unor elevi li se prezintă două drepte neparalele sub forma a două segmente ce nu se ating iar unii elevi ar putea considera că aceste drepte nu se intersectează. Este foarte important şă punem elevilor această întrebare, pentru că din răspunsurile greşite (că acestea ar fi paralele de vreme ce nu au nici un punct comun) vom putea vedea care elev nu a ajuns să înţeleagă cu adevărat fenomenul de dreaptă, spre deosebire de cel de segment. Desenul nu i-a ieşit foarte bine lui Hollinger, în figură pârând că dreptele se intersectează evident. Cel mai bine se înţelege fenomenul în doi paşi: pentru început desenăm două segmente ce nu se ating, dar ale căror drepte suport nu sunt paralele (pe vremea respectivă nu se prea vorbea de dreptele suport). În acest prim pas punem întrebarea dacă cele două drepte sunt paralele. Apoi, după un moment de gândire, eventual după ce am auzit prin clasă şi răspunsuri de felul că da, ar fi paralele, atunci, într-un al doilea pas prelungim segmentele respective pentru a arăta că dreptele nu sunt însă paralele (ca în figura completă IV.3 din manual). O variantă interesantă ar fi ca punerea întrebării să aibă loc în legătură cu două “drepte” desenate la marginea tablei, punctul lur de intersecţie fiind situat în afara teblei. Hollinger mai dă apoi şi un exemplu din spectrul iluziilor optice. Textul continuă apoi cu Postulatul lui Euclid, cu analiza acestuia şi cu două desene sugestive pentru lămurirea situaţiei. Pentru cei care doresc să vadă în detaliu aceste aspect ataşez cele două pagini despre care am vorbit (pag. 62-63), decupate doar cu ce ne interesează aici):


Dar să revenim la cuvinţelul nostru. Deci, putem vorbi liniştit de două drepte “cuprinse în acelaşi plan” (“situate în acelaşi plan“, sau cum a zis Hollinger: “din acelaşi plan“), în loc să folosim termenul mult mai riguros de “drepte coplanare”.
Oricum, veţi spune, tot se face referire la ideea de “plan”, iar asta ar trebui lămurită înainte. Şi da, aveţi dreptate, iar Hollinger a şi făcut-o, chiar la începutul manualului (care reprezenta totodată şi începutul geometriei, pe vremea respectivă începutul geometriei riguroase nefăcându-se în clasa a 5-a). Astfel, la începutul manualului găsim următoarele precizări, în cadrul primei lecţii (1.1 Planul. Punctul. Linia) găsim:
Planul. 1) O suprafaţă dreaptă şi netedă, ca de exemplu tăblia unei mese, tabla ş.a. reprezintă un plan. Mai precis, fiecare din ele reprezintă numai o parte din plan. Planul este nelimitat (nesfîrşit). Vom asemui planul cu o foaie de hîrtie sau de tablă foarte subţire, nu se ţine seama de grosimea ei, dar rigidă. Ea nu se poate încovoia, rupe sau găuri. (…)
Pe următoarea pagină găsim: 2. Punctul şi linia. Cînd atingem uşor hîrtia cu vîrful creionului, pe hîrtie apare un punct. Cînd mişcăm creionul astfel încît vîrful lui să alunece pe hîrtie, apare o linie. Orice linie este formată din puncte, aşezate unul lîngă altul, fără goluri între ele. (…) Punctul şi linia sînt figuri geometrice. Cu ajutorul lor se pot reprezenta obiectele din realitate, ele sînt modeleale acestor obiecte.
- Geometria plană. Unul sau mai multe linii sau puncte formează o figură geometrică. Cînd toată figura se găseşte într-un plan, se spune că figura este plană. De exemplu, triunghiul, dreptunghiul, cercul ş.a., sînt figuri plane. În cadrul acestei cărţi se expun proprietăţile figurilor plane. Această parte a geometriei se numeşte geometrie plană.
4) Figuri geometrice, puncte şi linii se pot desena şi pe un cilindru (un burlan sau o cutie de conserve), sau pe o sferă sau pe o altă suprafaţă, (…). Studiul acestor figuri nu intră în cadrul acestei cărţi. De asemenea, geometria se ocupăcu studiul unor corpuri, cum ar fi paralelipipedul, cilindrul sfera ş.a. Această parte a geometriei se numeşte geometrie în spaţiu. Pentru cei doritori de un studiu complet, ataşez aici şi paginile respective în integralitatea acestei prime lecţii (din pag. 3-5, rearanjate aici electronic în două pagini):


După cele două pagini introductive, de la începutul manualului, profesorul Hollinger putea liniştit să folosească expresia “două drepte din acelaşi plan”, fără a avea grija că încalcă nevoia de rigurozitate naturală a profesorilor de matematică, atâta cât se manifestă aceasta la nivelul matematicii gimnaziale, respectând totodată şi posibilităţile de înţelegere a elevilor din clasa a 6-a. Eu personal, oricum nu ţin minte să fi avut momente de neînţelegere.
Revenind în timpurile noastre, spre finalul acestui prim sfert al secolului XXI, eu cred că oricine poate la începutul geometriei, adică atunci, în clasa a 5-a, să povestească în felul acesta elevilor – 5 minute, cel mult 10 – despre plan, despre puncte sau linii, despre geometria plană şi despre geometria în spaţiu, fără a intra în detalii prea tehnice şi fără a apela, de pildă la renumitele reprezentări grafice ale unui plan în formă de paralelogram etc. Doar o poveste care apelează la exemple banale din lumea cunoscută a copiilor (mie îmi place exemplul cu geamul) este suficientă ca să lămurească ideea, iar apoi se poate folosi termenul liniştit.
Ca o observaţie colaterală, merită menţionat că Hollinger vorbeşte întotdeauna despre “plan”, adică la singular, şi nu despre “plane”. El vorbeşte despre “plan” şi despre “linii sau puncte”. Asta trebuie înţeleasă legat de observaţia de la început, cum se poziţionează mental elevul în 3D pentru a înţelege ce-i acela un plan, fără însă a avea în vizor preocuparea de a lucra apoi cu mai multe plane (specific clasei a 8-a), ci doar de a înţelege şi a descrie cât mai simplu “lumea” în care se va petrece geometria plană.
Dacă aţi studiat textul integral, aţi observat desigur că am omis o mare parte din text, de pildă partea cu alunecarea planului pe el însuşi. Nu o consider relevantă, nici clar folositoare la ceva anume. Am pus în copie prima lecţie integral, dar cred că se poate şi fără această parte, la fel şi fără partea despre feţele planului etc.
În finalul acestui articol, probabil că mulţi dintre dvs. se vor plânge de “un pic cam multă zdroabă pentru un singur cuvinţel! (mai exact exagerat de multă!)”. Totuşi, aici atingem un alt subiect foarte important, extrem de neglijat la ora actuală pe scară largă, anume acela de introducere a unei noţiuni noi. La ora actuală mulţi profesori văd începutul unei lecţii, respectiv partea de introducere a noilor noţiuni, drept o parte de mică importanţă, aproape neglijabilă. Cea mai importantă parte o reprezintă pentru mulţi partea de aplicaţii, cât mai complicate dacă se poate. Pe drumul către aceasta mulţi profesori doresc să parcurgă cât mai repede faza de introducere, de definire a noilor noţiuni sau de predare a teoremelor. Apoi, se aruncă cu mare avânt în aplicaţii cât mai “o-la-la!”. Astfel, cine mai are timp să piardă minute valoroase din oră pe lămurirea ideii de drepte coplanare? Pe bune?! Faptul că cei mai mulţi elevi nu înţeleg mare lucru, acest fapt este din păcate pentru mulţi colegi profesori un aspect total neglijabil.
Nici feed-back-ul primit de către aceşti colegi nu le dă de gândit: dacă la următorul test mulţi copii nu ştiu definiţia dreptelor paralele, atunci urmează o “ceartă zdravănă”, iar la următorul test profesorul ştie că dacă le dă din nou definiţia dreptelor paralele, iar “îi va fi bubuit”. Rezultatul este întotdeauna unul şi acelaşi: toţi ajung să-şi ia meditator particular şi uite aşa ajungem să avem “rezultate bune” cu clasa respectivă.
O componentă aparte a acestei situaţii sesizate aici o reprezintă rolul şi forma definiţiilor, aşa cum acestea au ajuns să fie înţelese în mentalul profesorului de matematică din acest început de secol XXI în şcoala românească. Se apropie tot mai mult momentul când îmi voi face curajul, încercând să abordez şi tematica definiţiilor în matematica şcolară.
Apropos de introducerea noţiunilor, trebuie totuşi să ne mai întoarcem la manualul lui Hollinger din anii ’70. Dânsul a mai aplicat o tehnică interesantă, care din păcate a cam fost abandonată odată cu reforma din 1980, astfel încât la ora actuală profesorii n-o mai cunosc. Este vorba despre introducerea noţiunilor prin predarea în spirală.
Astfel, în manualul respectiv (cel din 1977) Profesorul Hollinger vorbeşte prima dată despre dreptele paralele la paginile 20-21 în cadrul lecţiei 2.2. Relaţia de incidenţă, acolo unde apar pe scurt următoarele idei: Dreapta conţine o infinitate de puncte. (…) Printr-un punct se pot duce o infinitate de drepte. (…) Prin două puncte se poate duce o singură dreaptă. (…) Două puncte determină o dreaptă. (…) În această succesiune se ajunge apoi la: Intersecţia a două drepte conţine cel mult un punct. (…) Teoria respectivă se termină sec cu următoarea concluzie: Două drepte sînt ori concurente, ori paralele. (…)
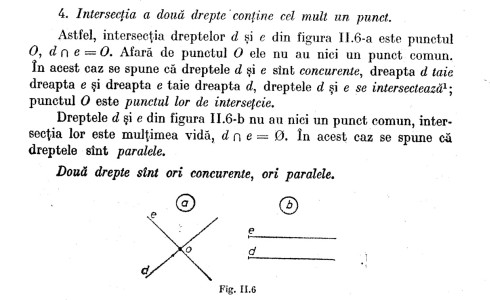
Am ataşat aici în imagine acest ultim pasaj al lecţiei respective, din care se vede că nu se dă nici cea mai mică atenţie ideii de coplanaritate, dar că Hollinger a pus deja de aici alăturat cele două poziţii posibile în care pot sta de fapt două drepte în geometria plană. După cum spuneam mai la începutul articolului, prezenţa acestor două imagini anulează din start posibilitatea ca vreun elev “să vadă” în acest moment şi varianta dreptelor necoplanare.
Dacă vrem să avem o abordare umană a introducerii noţiunilor, atunci nu ne vom arunca din prima într-o definiţie (elevii nu au de obicei capacitatea de a înţelege o noţiune din prima după o definiţie), ci undeva mai înainte vom intermedia contactul elevului cu acea noţiune într-o formă mai puţin teoreticistă, mai superficială. Hollinger a făcut-o aici în cadrul unui proces de analiză filozofică “în mişcare” intelectuală, folosind intens imaginile alăturate. Putem spune că oarecum elevii ajungeau să întâlnească pentru prima dată dreptele paralele în mod informal, în cadrul unui eveniment cu un cu totul alt subiect (poziţii relative a punctelor şi dreptelor). Cunoaşterea adevărată urma să aibă loc ulterior. Mai mult, în paginile următoare nu apăreau aplicaţii directe la dreptele paralele, doar că după o vreme elevii începeau totuşi să se întâlnească cu acestea în diferite ocazii, însă dar atât. De-abia după lecţia de la paginile 62-63 încep şi aplicaţiile (unghiurile formate de două paralele cu o secantă etc.).
Ca un aspect colateral, desigur că aţi observat aici, “v-a sărit în ochi”, modul de folosire “incorectă” a scrierii din teoria mulţimilor pentru exprimarea intersecţiei a două drepte într-un punct. Ceva de genul: “da’ pân-aici!”. Adică, folosim elemente din scrierea tipică mulţimilor acolo unde acestea ne uşurează scrierea (semnul de intersecţie în locul cuvântului respectiv), dar nu absolutizăm, deci nu îngreunăm scrierea în altă parte. Parcă îl aud spunând pe Hollinger că gândirea fenomenului geometric este oricum foarte grea, nu ne mai trebuie şi o îngreunare suplimentară pe baza aplicării radical-extremiste a scrierilor din teoria mulţimilor. Gen “pân-aici!”: Intersecţia a două drepte este un punct şi nu o mulţime. “Basta!”
Pentru cei ce mi-au urmărit scrierile din ultima vreme, desigur că puteţi sesiza apropierea acestui articol de ideea de “umanizare a matematicii şcolare” exprimată în interviul cu Dl. Profesor Radu Gologan, reluat de curând de la începutul anului 2022. În speranţa unor paşi în acest sens, pe curând! C. Titus Grigorovici
P.S. Apropos, “pe vremea mea”, acelea nu se numeau drepte “necoplanare”. Eu ţin minte destul de vag denumirea de drepte “strâmbe în vânt” (probabil, tradusă de unii din germană, unde se spune “windschief”; cred că am auzit această denumire în liceu sub forma de “necoplanare sau strâmbe în vânt”). Aruncând o privire şi în manualul de geometrie de a 8-a din 1978, am găsit expresia de “drepte oarecare”, pe care însă nu o consider deosebit de corectă. Nici măcar clasicul desen pentru drepte necoplanare nu apare acolo, ci doar un paralelipiped însoţit de referiri la anumite exemple de muchii, cât şi o imagine reprezentând o cale ferată (cu trenul aferent) ce trece peste o şosea (cu maşinile aferente), desenate în tehnica imaginilor des întâlnite in cărţile de la jumătatea secolului XX.
Oricum, celelalte două poziţii (paralele sau secante) erau şi în manualul respectiv descrise ca “două drepte din acelaşi plan“, în nici un caz drept “coplanare”. Cuvintele tehnic riguroase de “coplanare” respectiv “necoplanare” generaţia mea le-am auzit doar în clasa a 10-a, mai exact la o a doua trecere prin geometria plană. Este foarte important acest aspect: la o primă cunoaştere, termenii noi erau introduşi intuitiv şi într-un limbaj ne-tehnicizat excesiv, urmând ca la o a doua trecere lucrurile să capete clare accente de rigurozitate matură teoretic.
P.P.S. Când să declar articolul finalizat, inclusiv P.S.-ul de mai sus, mi-am dat seama că aş putea arunca o privire şi în manualele anilor 80′ (autori Ion Cuculescu şi Constantin Ottescu). Citez în continuare dintr-un manual din 1988 (îl am şi pe cel iniţial din 1979, dar şi o variantă din 1995, dinainte de marea schimbare din 1997). La pagina 3 manualul începe astfel:
(…) Anul acesta vom începe un studiu sistematic al geometriei. Vom studia o parte din geometria în plan, deci vom studia proprietăţi ale figurilor dintr-un plan dat, fixat. Aici merită deja intervenit: observaţi exprimarea mult prea pretenţioasă pentru copiii de gimnaziu mic (clasa a 6-a), exprimare de origine academică, ce presupune o privire matură, “de sus”, total nepotrivită copilului mic ce ia pentru prima dată contactul cu aceste cuvinte. De-abia apoi autorii îşi aduc aminte să prezinte ce-i acela un plan (tot la pag.3):
Planul este o noţiune abstractă, despre care ne facem o idee apropiată de cea exactă privind, de exemplu, o foaie netedă de hârtie, o pagină de carte, şi închipuindu-ne că această foaie este prelungită la infinit în toate părţile. În plus, această “foaie” nu are grosime. (…) Doar folosind cuvântul “abstract” şi autorii “i-au pierdut” din start pe mulţi copii. Privesc aici doar atitudinea, pentru că oricum copiii nu se apucă neapărat să citească manualul foarte riguros; mult mai des aceştia răsfoiesc manualul şi se uită doar la “poze”. Aşadar mesajul ridicării “lungumii de undă” al limbajului se adresa profesorilor, iar aceştia desigur că le explicau elevilor ce înseamnă aceea o “noţiune abstractă”. Sau nu? Interesant este că autorii erau total preocupaţi de prelungirea planului la infinit în toate părţile, cât şi de faptul că nu are grosime, neglijând total faptul că trebuie să nu fie curb (cum deseori sunt paginile unei cărţi, sau ale unui caiet la început). În manualul din 1995 (care avea pe lângă domnii de mai sus încă doi autori: Stefan Kleitsch şi Laurenţiu N. Gaiu) găsim însă următorul aliniat (pag.3):
Planul este o noţiune “abstractă”, despre care ne facem o idee apropiată de cea exactă privind, de exemplu, suprafaţa unei mese, placa de sticlă de la fereastră, o foaie netedă de hârtie (caiet), o pagină de carte şi închipuindu-ne că toate acestea sunt prelungite la nesfârşit “în toate părţiele”. În plus, vom considera că el nu are grosime. Aha! Deci a revenit “masa” lui Hollinger, respectiv masa pe care lucrează orice copil. Totodată, expresia “prelungită la infinit ” a fost înlocuită cu mai vechea dar şi mai accesibila “ la nesfârşit “.
Dar să avansăm cu această anchetă suplimentară. În manualul din 1988, la pagina 33 apar şi dreptele paralele. Lecţia începe astfel: Să considerăm două drepte diferite a şi b. Ele nu pot avea două puncte diferite comune, deoarece am văzut că prin două puncte trece o dreaptă şi numai una. Uau! Deci pe-atunci nu existau drepte suprapuse! Interesant. Citim mai departe: Se poate întîmpla ca două drepte diferite date a şi b să aibă un punct comun A. (… + figură) E poate întîmpla ca două drepte distincte să n-aibă nici un punct comun.
Definiţie. Două drepte diferite a şi b, care n-au nici un punct comun, se spune că sînt paralele. (… + figură) Interesant este că figura alăturată definiţiei nu prezintă două drepte paralele, ci două drepte clar neparalele, care însă nu se intersectează în zona figurii; aici nu există un desen cu două drepte paralele, ci doar se vorbeşte despre acestea; ciudat! Mult mai interesant e să observăm cum a evoluat situaţia în manualul din 1995 (pag. 92):
(…) dacă două drepte au două puncte comune, atunci ele au toate punctele comune şi se numesc drepte identice sau confundate; (… Aha!) Definiţie. Două drepte distincte (diferite) a şi b conţinute în acelaşi plan, care nu au nici un punct comun se numesc drepte paralele.
Deci, pe lângă revenirea la “posibilitatea” ca două drepte să fie suprapuse, vedem că a revenit şi condiţia ca dreptele paralele să fie “ conţinute în acelaşi plan “. Oricum, în 1995 sigur încă nu erau descrise ca două drepte “coplanare” în clasa a 6-a.
Închei aici aceste şapte pagini de zdroabă pentru un singur cuvânt, dar unul folosit în mod extrem de stupid, care terorizează masiv elevii, cu următoarea întrebare: “De ce şi de unde a apărut acest cuvânt în a 6-a?”. O sursă a unui răspuns posibil ar putea consta într-o interpretare prea riguroasă, prea “avântată”, din partea autorilor de manuale sau auxiliare, a unor elemente din Programa oficială din 2017, unde găsim următoarele cuvinte. În clasa a 5-a: Punct, dreaptă, plan, semiplan, semidreaptă, segment (descriere, reprezentare, notaţii). Apoi, în clasa a 6-a: Drepte paralele (…, deci fără aluzie la plan), dar şi Drepte perpendiculare în plan (…). What?