Ne-am preocupat în această scurtă serie despre cum putem proceda la clasă astfel încât numărul π să intre eficient în conştienţa elevilor. Am văzut în toamnă, cu ocazia alegerilor prezidenţiale că acest număr este cumva considerat ca un reper al delimitării persoanelor culte de restul populaţiei. Nu trebuie să fie un mare matematician, dar totuşi, uitarea lui π a reprezentat în aceste alegeri un element definitoriu al personajului respectiv, care ajunsese print-u joc ciudat al sorţii în poziţia de a se visa preşedintele României. Noi trebuie să predăm perimetrul şi aria cercului astfel încât π să nu rămână o enigmă pentru majoritatea elevilor, aşa cum din păcate se întâmplă deseori. Dacă ne structurăm predarea în mod sănătos, atunci peste ani, chiar şi după ce a intervenit uitarea, o persoană va ţine minte că există π şi că acesta este “cam 3,14”.
Una din marile provocări legate de acest număr o reprezintă faptul că acesta este un număr iraţional transcendent. Elevilor de gimnaziu nu le putem preciza clar aceste lucruri, dar le putem da un surogat interesant al ideii de număr iraţional (cu o infinitate de zecimale, dar neperiodic; atâta măcar trebuie să poată înţelege elevul de a 7-a), anume o imagine a preocupărilor despre caclularea lui π cu cât mai multe zecimale.
Astfel, undeva pe parcursul acestor lecţii ar fi frumos să le dăm elevilor ocazia să guste şi din acel subiect destul de ciudat prin care calculatoriştii se întrec în a-l determina pe π cu un număr cât mai mare de zecimale exacte. În acest context eu le duc elevilor la clasă copia unei pagini din cartea lui Simon Singh, Marea teoremă a lui Fermat, (Humanitas, 1998, pag. 60), unde este dat acest număr cu peste 1500 de zecimale. Tot în această lucrare se găsesc şi date despre numărul zecimalelor ale lui π cunoscut la acea vreme (anii ’90), dar acestea sunt oricum istorie, cartea respectivă având oricum o vârstă respectabilă de un sfert de secol. Pasionaţii de senzaţional pot căuta liniştiţi pe net situaţii mai apropiate de anii noştri.
Apoi le spun şi că în calculator îl am descărcat de peste 10 ani pe numărul π cu un milion de zecimale exacte (are 176 de pagini!), şi pot continua cu multe alte poveşti “vânătoreşti” despre cursa calculări acestui număr cu cât mai multe zecimale. Legat de acestea, desigur că le putem preciza elevilor că aceste rezultate sunt obţinute pe alte căi decât cele direct geometrice accesibile elevului de gimnaziu, şi că despre aceste căi vor putea căpăta o primă impresie de-abia în liceu, cei care vor merge mai spre matematică (desigur, o primă impresie şi aceasta extrem de superficială). Revenind la elevii din gimnaziu, adică la nivelul de cultură generală predat aici, chiar şi următoarea valoare aproximativă cu 50 de zecimale exacte este suficient de covârşitoare:
π ≈ 3,14159265358979323846264338327950288419716939937510…..
(Da, sunt conştient că nu ar trebui să folosesc într-o scriere atât semnul de aproximaţie cât şi notaţia de neterminat de la sfârşit, dar cele două arată atât de bine împreună!) În acest context este absolut impresionantă pentru elevi, chiar şi pentru cei orientaţi mai umanist (Salut! Vlăduţ) să afle că oamenii au găsit o metodă ciudată, dar eficientă, de a memora acest număr cu ceva mai mare exactitate decât doar două zecimale, anume prin asocierea cu o propoziţie artificială, dar mai uşor de memorat (dar mai uşor de memorat decât un număr de cifre venite de-a valma), a cărei cuvinte au lungimea cifrelor din exprimarea lui π. Această tehnică mnemonică a primit şi un nume: piphilologie (noi le-am spus pi-isme)
Astfel, în limba română avem următorul exemplu de propoziţie pentru zece cifre (primită încă din liceu de la mama mea): Aşa e uşor a scrie renumitul şi utilul număr mare, cu lungimea cuvintelor corespunzând aproximării 3,141592654 (cu 9 zecimale exacte, la care se adaugă ultimul 4 ca aproximarea mai bună prin adaos a lui 3).
Apropos, de dragul unei cât mai apropiate exactităţi, pentru cazurile când nu ne ajunge clasicul 3,14 şi vrem o aproximare cât mai exactă cu patru zecimale, în loc de 3,1415 nu ar fi mai bine să le atragem atenţia elevilor asupra valorii 3,1416, aceasta fiind o aproximare mult mai bună datorită acelui 9 de pe poziţia a cincea zecimală? (zic şi eu, doar aşa “ca să mă bag în seamă”…). Precizez aceste aspecte şi din punct de vedere psihologic: o discuţie despre când ar trebui folosită aproximarea în lipsă şi când aproximarea prin adaos poate fi sterilă dacă se face pe example aleatorii. Dimpotrivă, în situaţia de faţă numărul π a căpătat deja în mintea elevilor o oarecare identitate, reprezentând în preocuparea ultimelor ore un adevărat “personaj” în lumea asta ciudată a matematicii. Ca atare π poate trezi interesul şi atenţia elevilor în mult mai mare măsură, clasa putând fi mai uşor atrasă într-o preocupare de detaliu cum este dacă să luăm aproximarea prin lipsă sau prin adaos. Desigur că există şi alte criterii pe baza cărora să facem această alegere, dar aici, pe baza acestei situaţii din cadrul numărului π, putem prezenta eficient criteriul celei mai bune aproximări.
Revenind la propoziţiile care-l dau pe π, în limba engleză avem “paşnica”: How I wish I could recollect pi easily today! sau simpatica: May I have a large container of coffee beans?, cu lungimea cuvintelor pentru aproximarea 3,14159265 (tot opt zecimale exacte), eventual varianta cu două cifre în plus: May I have a large container of coffee, cream and sugar? (10 zecimale). Mult mai “rebelă” este în engleză următoarea propoziţie, potrivită mai degrabă studenţilor: How I need a drink, alcoholic of course, after the heavy lectures involving quantum mechanics (14 zecimale, merge până la secvenţa 79).
În franceză gluma se îngroaşă: Que j’aime à faire apprendre un nombre utile aux sages! Glorieux Archimède, artiste, ingénieur, Toi de qui Syracuse aime encore la gloire, Soit ton nom conservé par de savants grimoires! (30 de zecimale, pe care însă nu le-am verificat). Oricum, francezii “au luat-o rău pe arătură”, pentru că la această reprezentare în versuri există şi o variantă pentru obsedaţi (ca să nu spun maniaci):
Que j’aime à faire apprendre ce nombre utile aux sages!
Immortel Archimède, artiste ingénieur,
Qui de ton jugement peut priser la valeur?
Pour moi, ton problème eut de pareils avantages.
Jadis, mystérieux, un problème bloquait
Tout l’admirable procédé, l’œuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
Ô quadrature ! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l’espace plan circulaire?
Former un triangle auquel il équivaudra?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire
Fonction du rayon. Pas trop ne s’y tiendra:
Dédoublera chaque élément antérieur;
Toujours de l’orbe calculée approchera;
Définira limite ; enfin, l’arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèle
Există astfel de propoziţii şi în alte limbi. Iată una în spaniolă: Fue y cayó. Y queda solamente la inútil cifra con pocos destinos poderosos, tristes devenires sin el más sencillo bien. Idiota, re idiota, sabe que sus encantos son ya latosos decimales. Pobre…, dar şi una în portugheză: Cai a neve e novas ferrovias de marfim serão por casas trocadas, sau una deosebit de sugestivă în portugheza braziliană: Sim, é útil é fácil memorizar pi, grande valor real. În italiană traba ar suna cam aşa: Non è dato a tutti ricordare il numero aureo del sommo filosofo Archimede. Certuni sostengon che si può ricordar tale numero, ma questi soli poi non recitano che un centone insensato (30 de zecimale).
Majoritatea acestora se găsesc pe Wikipedia, unde apar ca “tehnici mnemonice” sub denumirea de Piphilology. La adresa https://en.wikipedia.org/wiki/Piphilology găsim exemple din mai multe limbi. Aici apare şi varianta primită de la mama mea, dar şi o altă variantă în română, “în versuri”:
Dar o ştim, e număr important ce trebuie iubit,
Din toate numerele însemnate diamant neasemuit,
Cei ce vor temeinic asta preţui
Ei veşnic bine vor trăi.
P.S. Fără nici o legătură directă cu numărul π, amintesc că există astfel de asocieri mnemotehnice cu o propoziţie şi pentru numărul e. Iată două variante primite tot de la mama mea: Un scoţian a inventat, un elveţian a calculat şi exprimat acel număr admirabil (e vorba despre John Napier şi Leonhard Euler). Tot pentru o aproximare cu 12 zecimale exacte a numărului e ≈ 2,718281828459 avem şi: Pe numărul e savantul îl stimează, e academic şi formează bază pentru logaritmi.
Ca un fapt divers din lumea matematicienilor (cu evidentă tentă comică), vreau să vă spun că clădirea departamentului Facultăţii de matematică de la Universitatea Babeş-Bolyai din Cluj – Mathematica – îşi are sediul într-o clădire ce cuprinde, printre altele, biblioteca facultăţii, încăperi pentru toate catedrele, cât şi două săli de curs, numite desigur sala π şi sala e (cum altfel?).
Noi am găsit şi la Paris, în Palais de découverte (un fel de muzeu al ştiinţelor, pe care l-am amintit mai sus) o sală π rotundă, la capătul coridorului despre matematică, care chiar este folosită ocazional la diferite prezentări. Numărul π este scris la baza tavanului, cu sute de zecimale, dând roată sălii de câteva ori, iar sub acesta un rând cu mari matematicieni din toate timpurile (îi găsim evocaţi acolo atât pe Ahmes, scribul Papirusului Rhind, dar şi pe Bolyai; puteţi face o tură virtuală a acestei săli la adresa https://www.youtube.com/watch?v=NRuKh7dI_bs ). Ataşez o poză cu familia mea din 2007 în această sală. CTG
P.P.S. Haideţi să mai evocăm încă o ciudăţenie despre numărul cercului, doar aşa ca să vedem că am putea continua în ritmul acesta mult şi bine. Pentru asta trebuie să luăm în discuţie şi celelalte două numere iraţionale foarte des folosite, numărul pătratului şi numărul triunghiului echilateral, adică 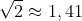 şi
şi 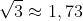 cu aproximările lor uzuale cu două zecimale exacte. Verificând pe aceste aproximări suma lor 1,41 + 1,73 = 3,14, putem vedea ciudăţenia cea mai mare:
cu aproximările lor uzuale cu două zecimale exacte. Verificând pe aceste aproximări suma lor 1,41 + 1,73 = 3,14, putem vedea ciudăţenia cea mai mare: 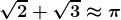 .
.

