Anul trecut şcolar am avut două clase paralele de a 5-a, aşa încât eu personal am putut evolua de două ori mai mult în lecţiile specifice. În prima parte a prezentului eseu “am ajuns cu elevii” până la momentul când aceştia au descoperit existenţa şi fenomenul fracţiilor zecimale periodice, pe baza câtorva exemple la clasă, dar şi la temă.
Pentru mine este foarte important ca în acest moment elevii să vieţuiască în mod sănătos diversitatea fracţiilor periodice. Atenţionez că procesul trebuie să se întâmple într-un ritm accesibil majorităţii elevilor, astfel încât aceştia chiar să şi înţeleagă ce se petrece. Această recomandare vine desigur în opoziţie cu impulsurile spre o viteză cât mai mare de parcurgere a lecţiei, conducând la o cantitate tot mai mare de informaţii, viteză spre care au fost împinşi profesorii în anii ’80-’90. Gândul acestei recomandări ţinteşte spre o accesibilizare a vitezei şi a cantităţii de lucru la nivelul majorităţii elevilor (mă refer aici mai ales la clasele cu colective eterogene). Din această temperare a impulsurilor mele elitiste de profesor face parte şi ideea de a relua la începutul orei următoare cele întâmplate şi descoperite pănă acum, aşa ca o mică recapitulare. În acest sens am văzut în pozele de tablă de la sfârşitul primei părţi unele tentative de sistematizare pe scurt a celor deja descoperite până în acel moment.
În setul de exerciţii sugerat în prima parte a prezentării am inclus şi impărţiri cu două cifre în perioadă, dar şi cu patru sau şase cifre în perioadă (împărţirea la 101 respectiv la 7). Tehnic, am putea renunţa pentru prima zi la împărţirea la 7 (adică la perioada de 6 cifre), lăsând-o ca “surpriză” pentru a doua oră a temei fracţiilor zecimale periodice (eu de multe ori aşa am făcut şi este de-a dreptul interesant când eu mă contrazic pe mine faţă de ce-am spus în prima parte; de fapt vreau să vă arăt diferite variaţiuni posibile ale lecţiei).
În această a doua prte a eseului de faţă va fi activ un principiu despre care încă n-am vorbit, aşa că o fac acum. Este sănătos pentru predare ca noi să ştim mai mult decât le aducem elevilor în clasă. Elevii capătă cu timpul o siguranţă în profesor dacă simt, chiar nearătat, că acesta ştie mult mai mult decât le arată lor. Este penibil dacă elevii te surprind prea des cu întrabări la care nu ai răspuns şi faţă de care te eschivezi (gen: acum n-avem timp pentru asta). Pe de altă parte, dacă uneori, rar, chiar se întâmplă, atunci eu prefer să fiu cinstit şi să spun că nu ştiu; asta mă umanizează în faţa lor. Dar, desigur, trebuie să nu se întâmple prea des.
Revenind, îÎn plus, din acea zonă vastă de cunoştinţe suplimentare profesorul poate scoate din când în când câte o idee, dacă consideră că este sănătos pentru clasă (de fapt asta fac toţi colegii în sistemul olimpic, elitist, dar o fac doar în zona problemelor). În cazul de faţă ajută dacă noi cunoaştem de unde se obţin perioade cu 2, cu 3, cu 4, cu 5 sau 6 cifre. Elevilor nu le explicăm de unde “le scoatem”, decât eventual în finalul capitolului.
*
Deci, de unde obţinem o împărţire cu trei cifre în perioadă? Repet: acum vorbesc pentru profesori (!!!); elevii nu au de unde să ştie a răspunde la această întrebare. Sau, la ce trebuie să împart astfel încât să obţin o perioadă de patru cifre? Cu această mega-întrebare ar trebui să ne ocupăm în continuare. Eu mi-am pus-o de câţiva ani buni şi iată cum am raţionat.
Pentru început ar trebui să recapitulăm ce cunoaşte sigur orice profesor (adică ce cred eu că este cunoscut). impărţirile la 2, la 5, la puteri ale acestora sau la numere compuse doar din factori de 2 şi 5, dau un număr finit de zecimale (în plus faţă de deîmpărţit), egal cu exponentul cel mai mare al împărţitorului scris ca produs de puteri de factori primi (astfel de exprimări “ne ies pe gură” dacă ne punem în cap să vorbim cât mai riguros; cam ce-aţi simţit dvs. la citirea acestei fraze, cam asta simt elevii când “îi duduim” cu câte o exprimare de-a noastră prea riguroasă). Fraza de deasupra este valabilă dacă nu are loc o simplificare prin 2 sau 5; atunci lucrurile trebuie reanalizate după simplificare (oare cum ar fi sunat fraza cea complicată dacă aş fi inclus şi ultimul aspect în ea?).
Un al doilea aspect pe care cam toţi profesorii îl ştiu este că împărţirea la 3, la 6 şi la 9 dă perioadă de o cifră. De unde vin atunci perioadele de mai multe cifre? Păi, de la alte numere! Dar, de la care? Unii profesori cunosc că împărţirea la 11 dă perioadă de două cifre. Dar, de ce? Poate unii au observat că o împărţire de felul 37 : 22 va da o perioadă de două cifre precedată de o cifră zecimală izolată (adică o fracţie zecimală periodică mixtă). Este destul de clar că acea cifră izolată provine de la factorul 2, iar perioada de două cifre de la factorul 11. Un bun exemplu aici ar fi o împărţire la 88 = 23 · 11, care va da o fracţie periodică mixtă cu … (aţi înţeles, da?).
Un al treilea aspect cunoscut nouă, profesorilor, dar elevilor încă nu, este felul în care se transformă fracţiile zecimale periodice în fracţii ordinare, adică renumitele scrieri cu atâţia de 9 la numitor câte cifre în perioadă (numitorii de felul 9. 99. 999, 9999, ….) la care se adaugă şi combinaţii de tipul 990, 900, etc.
La toate acestea se mai adaugă un aspect de obicei necunoscut, dar pe care eu îl ştiam, anume descompunerea numărului 1001 = 7 · 11 · 13. Precizez că 1001 se compune multiplicativ exact din “următoarele trei numere prime”, adică exact cele ce urmează după primele trei numere prime (2, 3, 5), care sunt cunoscute şi uzate de obicei. Această descompunere apare folosită magistral într-un număr vechi de magie matematică. Iată-l pe scurt: magicianul îi cere subiectului (unui voluntar din audienţă, unuia care ştie bine socoti) să scrie la alegere un număr de trei cifre diferite (magicianul nu vede numărul respectiv). Apoi subiectul magiei este rugat să scrie în continuarea numărului încă o dată cele trei cifre, obţinând un număr de şase cifre (de pildă, la numărul 735 se va obţine numărul 735735). Apoi, acest număr trebuie împărţit la 7 (împărţirea se face exact); apoi, rezultatul va trebui împărţit la 11 (din nou iese împărţire exactă, adică fără rest). În final ultimul rezultat trebuie împărţit la 13 (desigur că se divide şi la 13). Magia este că după cele trei împărţiri, rezultatul final este exact numărul iniţial ales (adică exact 735).
Eu fac acest număr de magie trecând calculele de la un elev la altul, implicând astfel mai mulţi elevi. Surpriza va fi şi mai mare când ultimul elev îi poate spune primului elev numărul ales (pe care doar el şi următoarul îl ştiau). După efectuarea numărului de magie îi provoc pe elevi să-l descifrăm, adică să vedem cum de s-a întâmplat chiar aşa. Problema are două aspecte: primul ar fi că alipirea unui număr de trei cifre după acesta înseamnă de fapt o înmulţire cu 1001 (adică 735 · 1001 = 735735). Aici trebuie pur şi simplu făcută această înmulţire pentru a vizualiza ce se întâmplă; al doilea aspect este chiar descompunerea numărului 1001. S-ar putea ca un elev să se prindă de legătura cu cele trei numere ce apar ca împărţitori succesivi, sau se prea poate să fie nevoie ca profesorul să le spună acest fapt. Acest număr de magie mi-a fost foarte de folos la studiul periodicităţii ce apare la împărţirea la 7. Să revenim deci la studiul ce l-am propus.
Cercetarea noastră poate începe de la perioada de două cifre, care este legată de numărul 99 = 9 · 11. Numărul 9 apare prima dată ca factor chiar la numitorul 9, al perioadelor de o cifră. Doar numărul 11 apare prima dată ca factor la 99, deci la numitorul perioadei de două cifre (dacă aveţi comentarii legate de exprimarea neriguroasă, să ştiţi că o fac intenţionat ca să fie mai accesibilă). De aici apare întrebarea, conexiunea absolut legitimă: ce numere apar noi ca factori în acest proces, ca divizori ai numerelor cu cifre doar de 9, în studiul de creştere a numărului de cifre de 9? Adică, ce factori noi apar la 999, sau la 9999, sau la 99999? Sau invers: de vreme ce am văzut că împărţirea la 7 dă perioadă de şase cifre, înseamnă că factorul prim 7 apare prima dată ca divizor al numărului 999.999, respectiv mai exact la numărul 111.111?
Oare, aţi prins ideea de unde am dedus toate cele? Dacă da, atunci opriţi-vă din citit, luaţi hârtie şi creion şi studiaţi singuri mai departe. Dacă nu v-aţi prins ce vreau să sugerez, atunci puteţi lectura prezentarea în continuare.
Numărul 111.111 este de tipul celor de la numărul de magie matematică de mai sus. Ca urmare deducem că 111.111 = 111 · 1001, având astfel ca divizor pe 7. Deoarece numărul 111.111 este primul de tipul 11…1 care se divide la 7, rezultă că împărţirea la 7 dă perioadă de şase cifre. Doar de curând “mi-a picat fisa” că desigur şi la împărţirea cu 13 vom obţine o perioadă tot de şase cifre. Evident!
După ce am înţeles acestea merită să ne întoarcem şi să o luăm sistematic. 11 este el însuşi număr prim. Primul unde putem pune în discuţie ce am observat la 7, este numărul 111, care este divizibil cu 3. Aşadar 999 = 33 · 37. Deducem că la împărţirea cu numărul prim 37 se obţine perioadă de trei cifre. Asta o ştiam mai de mult timp. dar prin primăvară mi-am dat seama că avem perioadă de trei cifre şi la împărţirea cu 27, care însă nu este prim. Totuşi, ca divizor el apare prima dată la numitorul 999, asta însemnând că şi el generează perioade de trei cifre (ce bun e calculatorul de pe telefon ca să verifici repede astfel de afirmaţii!).
Următoarea întrebare la rând este despre descompunerea lui 1111. În mod similar cu fenomenul de la şase de 1, preluat de la magia de mai sus, vom putea spune şi aici că 1111 = 11 · 101. Numărul 101 fiind număr prim, iar 11 apărând deja ca divizor la 99, deducem că factorul 101 este cel mai mic număr care generează perioadă de patru cifre.
Oare, care este cel mai mic divizor al lui 11.111? Aici m-a ajutat nevastă-mea, care din plictiseală (în timpul unei şedinţe) a abordat problema din altă parte. Astfel, ea lua numere ciudate şi le studia cu ce ar trebui să le înmulţească astfel încât să obţină produse numere scrise doar cu cifra 9, adică de tipul 99…9. Pe această cale la găsit ea pe 41 ca divizor al lui 99.999 (mai exact 11.111 = 41 · 271). În poza următoare găsiţi exemplificarea metodei chiar pentru 41. Am încercat să fac separat fiecare pas într-o imagine nouă, evidenţiind pasul nou cu roşu. Prima cifră cu care începe un pas este cea roşie din mijloc, stabilită astfel încât să completeze suma pe coloana respectivă la 9; în funcţie de aceasta se stabileşte şi cifra din acel pas de la înmulţitor, iar apoi se revine în mijloc şi se completează produsul pasului respectiv. Finalul procesului este atunci când obţinem direct o sumă de 9, nemai fiind nevoie să o completăm cu nimic; această sumă directă de 9 este prezentată în forma finală cu albastru. Interesant, ce se mai poate face în timpul unor şedinţe prea lungi!
Rezumând, vom obţine perioadă de două cifre la 11, perioadă de trei cifre la împărţirea cu 27 sau 37, perioadă de patru cifre la împărţirea cu 101, perioadă de 5 cifre la împărţirea cu 41 şi perioadă de şase cifre la împărţirea cu 7 sau cu 13. Asta cu împărţitori cât de cât accesibili; pe 271 nu l-am băgat în seamă pentru că sigur nu vreau să îl folosesc, nici la clasă cu elevii, nici eu singur acasă (dar se poate verifica cu telefonul, de la 11.111 = 41 · 271).
Repet, desigur că toate aceste gânduri nu sunt menite să ajungă la elevi, nu sunt pentru ei. Acest studiu, ca o mică cercetare, a fost menit doar să ne ajute pe noi să găsim exemple diverse pentru elevi, cu împărţiri având la rezultat perioade mai lungi de o cifră, aşa încât elevii să priceapă din start acest aspect: că pot exista perioade de diferite lungimi, iar asta nu doar pe bază de încredere (doar aşa, că le spunem noi, iar ei ne cred “pe cuvânt”), ci chiar vieţuind asta, adică prin efectuarea unor împărţiri. Este important acest aspect, pentru ca elevii să nu se uite “ca mâţa-n calendar” la lecţia următoare, atunci când îi vom învăţa să transforme fracţiile zecimale periodice înapoi în fracţii ordinare, şi unde acolo avem cu mare conştiinciozitate exemple cu perioade de diferite lungimi. Elevii nu trebuie să ştie mare lucru din studiu de mai sus. Ei trebuie doar să primească atât la clasă, cât şi la temă, câteva exemple cu perioade de alte lungimi, nu doar exemple cu perioade de o cifră. Dar, vedeţi câtă nebunie de gânduri stă în spatele celor câteva exemple din lista de exerciţii dată ca sugestie în finalul primei părţi.
Vedeţi acum şi de ce în prima parte a eseului am făcut acea ciudată delimitare pe categorii de dificultate a împărţirilor din primul semestru. Avem pentru început împărţirile la numere de o cifră la care se mai adaugă împărţirile foarte uşoare la 10 şi la 11. Aha, la 11! Deci, pe lângă perioadele de o cifră, le putem oferi împărţiri destul de accesibile cu perioada de două sau şase cifre. Apoi, am spus atunci şi deîmpărţiri cu şirul multiplilor accesibil sau parţial accesibil, aici intrând 15 sau 12 (care dau fracţie periodică mixtă) sau 13 (care dă fracţie periodică de şase cifre). Apoi vorbeam la început şi de împărţiri care s-ar mai putea face relativ uşor, cum sunt împărţirile la 101 (patru cifre la perioadă) sau la 41 (cu cinci cifre la perioadă). Cele mai greuţe mi se par împărţirile la 27 sau la 37 (care amândouă generează o perioadă de 3 cifre).
*
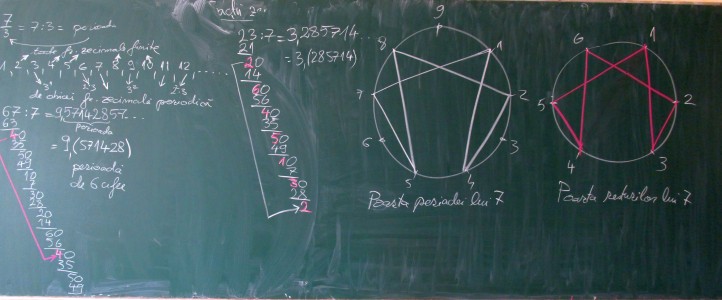
În cadrul acestui pasaj de împărţiri ce dau ca rezultat fracţii zecimale periodice, eu am pentru elevi şi două momente speciale. Primul ar fi cel ce l-am numit “poarta lui 7” cu două forme uluitor de asemănătoare: “poarta perioadei împărţirii la 7”, respectiv “poarta resturilor intermediare ale împărţirii la 7”. Am vorbit despre acest fenomen ciudat în postarea din 2020 de la adresa http://pentagonia.ro/poarta-impartirii-lui-7-studiul-grafic-pe-cercul-de-9-cifre/ şi vă rog să-l studiaţi în acest moment, ca să nu mai reiau acele idei. În pozele de tablă de la sfârşitul acestei a doua părţi vor apărea din nou exemple în acest sens.
Suplimentar la cele spuse atunci sau la cele ce apar în poze, vă propun şi un exerciţiu de cercetare descoperit personal la începutul acestei săptămâni în care scriu rândurile de faţă. De vreme ce la numărul 111.111 apar pentru prima dată ca divizori noi ai numerelor de tipul 11…1 numerele prime 7 şi 13 (11 apăruse înainte, ca divizor al lui 99), iar la împărţirea cu 7 avem perioada de şase cifre, deducem două informaţii: şi la împărţirea la 13 vom avea perioadă de şase cifre (am mai spus asta şi este foarte uşor de verificat cu telefonul), dar şi că la împărţirea cu 13 ar trebui să apară o reprezentare grafică similară cu poarta lui 7, un fel de “poarta lui 13”. Vă las pe dvs. să studiaţi şi să savuraţi veridicitatea acestor supoziţii. Atenţionez totodată că această asemănare absolut surprinzătoare între comportamentul împărţirii la 7 şi al împărţirii la 13 nu are decât cel mult o legătură de tip misticist cu faptul că 7 + 13 = 20, care reprezintă exact numărul degetelor unui om.
Un al doilea moment special ar fi cel doar amintit în eseul despre conflictul cognitiv. Pe acesta aş vrea să-l detaliez în următoarele rânduri. Astfel, elevilor le-am adus următoarea întrebare, ca dilemă cognitivă: dacă împărţim un număr (desigur impar) la 2 (adică la 21), vom obţine un cât cu o cifră zecimală; dacă împărţim un număr impar la 4 (adică la 22), vom obţine un cât cu două cifre zecimale; dacă împărţim un număr impar la 8 (adică la 23), vom obţine un cât cu trei cifre zecimale şi tot aşa mai departe (nici n-am mai precizat denumirea de fracţii zecimale finite). Acelaşi lucru se întâmplă la împărţirea cu puteri ale lui 5. Dimpotrivă, dacă împărţim un număr la 3 (desigur, unul nedivizibil cu 3), atunci vom obţine o fracţie zecimală periodică cu o cifră în perioadă; dacă însă împărţim un număr la 9 (desigur, la fel, unul nedivizibil la 3), atunci vom obţine o fracţie zecimală periodică tot cu perioadă de o cifră; oare ce se va întâmpla la împărţirea unui număr la 33 = 27? Vom avea tot perioadă de o cifră sau vom avea perioadă de trei cifre? Sau poate o altă situaţie?
Această întrebare, evident destul de îmbârligată, ce necesită o concentrare bună, această întrebare clasele în ansamblu au înţeles-o. Aici a fost momentul când un elev a exclamat: “E aşa de palpitant că eu nu mai pot; vreau să aflu cum se întâmplă” (sau ceva de genul acesta, că desigur nu m-am oprit să-i notez vorbele). Prima parte a afirmaţiei era de mult lămurită; împărţirile la 3 şi la 9 erau proaspete (de ora trecută), aşa că nu aveam decât să facem o împărţire la 27.
Legat de afirmaţia de mai sus, despre cât ar trebui să cunoaştem noi ca profesori în plus faţă de ce le aducem elevilor, la una din clase s-a ivit întrebarea despre ce se întâmplă la împărţirea la 34 = 81. Vă las pe dvs. să studiaţi ce se întâmplă aici.
Nu am pretenţia că am lămurit subiectul cu totul, dar vedeţi câte gânduri se află în spatele unei banale lecţii, dacă vrei să respecţi mintea curioasă şi gândirea vie a elevilor. Din păcate, majoritatea profesorilor vin la lecţia respectivă cu împărţiri generând doar perioade de o cifră, cel mult două, prin aceasta contribuind din nou la înceţoşarea gândirii elevilor. Chiar şi dacă un elev ar întreba aici – mânat de o curiozitate naturală, dintr-o gândire trează – dacă profesorul nu ştie ce să-i răspundă, momentul este ratat (ca să nu mai spun că profesorul respectiv “s-a făcut de …”).
Pe de altă parte, nu cred că am exagerat în studiul meu, de vreme ce m-am dus doar până la perioade de şase cifre, corespunzând împărţirii accesibile la 7 (care e un număr de o cifră). Ce se întâmplă mai încolo chiar nu mă mai interesează.
Vedem însă cum această a doua parte a studiului despre predarea fracţiilor zecimale periodice se adresează în mare parte doar înţelegerii fenomenului de către profesor, astfel încât acesta “să-şi umple tolba” cu o varietate sănătoasă de exemple. Această a doua parte a studiului despre fracţiile zecimale periodice este adresată doar profesorului. De-abia cândva după ora următoare am putea “la o adică” să-i provocăm pe elevii cei mai buni (doar pe aceştia) cu o întrebare despre sursa diferitelor lungimi ale perioadelor. Poate fi o discuţie de câteva minute, care doar să atingă subiectul şi să sugereze de unde vin acestea, sau poate să vină ca un studiu de o oră extra, în cazul unei clase foarte bune, după parcurgerea materiei, cândva în ultimele ore înainte de vacanţa mare.
Închei aici cu un nou pachet de poze de tablă din lecţiile ultimului an, în care puteţi regăsi anumite aspecte discutate aici (nu neapărat exact în forma descrisă acum). Precizez că lecţiile respective s-au desfăşurat în regim de “eu la tablă iar elevii pe caietul lor”. De pildă, uneori scriam eu în faţă, apoi elevii trebuiau să meargă singuri înainte, fiecare în caietul său, iar apoi – după ce destul de mulţi terminaseră – făceam şi eu calculele pe tablă, atât ca verificare pentru cei care au făcut, cât şi pentru completarea notiţelor celor care nu s-au priceput. În partea a treia a prezentului studiu vom analiza lecţia inversă, anume transformarea fracţiilor zecimale periodice în fracţii ordinare. C.Titus Grigorovici