(amintiri matematice din copilărie)
Iarna este anotimpul şezătorilor. Stând împreună cu cei dragi ne cuprinde nostalgia şi începem să depănăm amintiri. Într-o astfel de zi, iarna trecută, am început să “aştern pe hârtie” amintirile matematice din copilăria mea. Gândul a fost unul foarte clar: de a arăta care sunt sursele ideeilor susţinute cu atâta hotărâre în postările PENTAGONIA. Eseul se dorea un prim capitol, unul strict personal, intim, în preocuparea mai largă despre lămurirea situaţiei actuale a învăţământului matematic preuniversitar românesc, prin clarificarea rolului jucat de reforma impusă de Ceauşescu în finalul anilor ’70 şi începutul anilor ’80. Până la urmă materialul a crescut prea mare, aşa că a fost fragmentat şi doar o parte din acesta a fost publicată sub titlul de Reforma uitată. Acum, este iarăşi iarnă, şi privim în urmă la un an neobişnuit. Poate că acum este vremea să depănăm nişte amintiri din copilărie. Sper că le veţi savura, chiar dacă uneori sunt scrise stângaci, având convingerea că unele dintre ele sunt într-adevăr întâmplări remarcabile. Dar, mai presus de orice, pentru mine ca profesor, amintirile din copilărie, ale mele sau ale altora, reprezintă ferestre deschise spre sufletul şi mintea copiilor în general, faţă de care noi ca adulţi avem obligaţia să ne adaptăm şi să ne calibrăm nivelul predării.
Prof. Constantin Titus Grigorovici
*
M-am născut şi am crescut în Oraşul Victoria, la marginea judeţului Braşov, având zilnic o privire superbă asupra munţilor Făgăraş. Părinţii mei Grigorovici Maria şi Vasile au fost amândoi profesori de matematică la liceele din oraş. Tata a reuşit chiar performanţa de a preda în acelaşi liceu de la repartiţie, din prima zi de activitate, neîntrerupt până la pensionare. Mama nu a reuşit aceasta pentru simplul fapt că liceul la care era titulară a fost desfiinţat pentru vreo 15 ani. Mama era din Şimleul Silvaniei iar tata din Vatra Dornei, nimerind amândoi în celălat vârf al unui triunghi, parcă paraşutaţi printre străini în ţara Făgăraşului. Luaseră acolo repartiţie la teminarea facultăţii în 1965. Eu am apărut prin zonă în 1967, pe ecourile Beatles şi Phoenix, odată cu marile evenimente flower power din lumea largă.
Bunicul din partea tatălui avea un mic magnetofon cu care m-a înregistrat când eram copil mic. Astfel, din difuzor se aude întrebarea Ce vrei să te faci când o să fi mare? Şi apoi vine răspunsul dat de o voce dulce de copilaş: pofesol de mametatică!
În apartamentul din care am primele amintiri, zugravul – la cererea tatălui meu – a pictat pe un perete din holul de la intrare Teorema lui Pitagora! Da, aţi înţeles bine, eu am crescut văzând zilnic pe perete figura cu cele trei pătrate construite în exteriorul unui triunghi dreptunghic, alături de un palmier stilizat. Aşa gândise zugravul respectiv, teorema lui Pitagora alături de un palmier, pictate în holul d-lui profesor de matematică. Nu pot preciza când am înţeles această teoremă, cred că tot în clasa a VII-a, ca toţi copiii, dar desenul îl cunosc de când mă ştiu. Cu durere mă gândesc la generaţii întregi de elevi care nici nu mai ajung să cunoască această figură, una dintre cele mai cunoscute, dacă nu cea mai cunoscută figură geometrică. Între timp există şi profesori tineri care nu o cunosc. Ultima dată am văzut această figură la loc de cinste pe culegerea profesorului Gheba din 1996.
Când eram în clasa a VI-a părinţii mei s-au mutat în apartamentul vecin şi de-atunci până la plecarea la facultate am locuit la cea mai fabuloasă adresă posibilă: Or. Victoria, str. Victoriei, bloc 10, ap.10. Da, ciudată-i şi karma asta! Părinţii mei locuiesc şi acum în acest apartament.
Amintiri speciale legate de matematică, dar din afara şcolii, mai am şi din timpul gimnaziului: eram cu părinţii la mare şi tata tot desena şi colora forme ciudate pe foi de hârtie. Întrebând despre ce face am înţeles că era vorba despre o mare problemă – problema celor patru culori – pe care nimeni încă nu a rezolvat-o. Ulterior am regăsit-o ca student, iar ca profesor am aflat că a fost „rezolvată” cu un calculator; interesant că rezolvarea cea controversată s-a făcut cam în anii când îl vedeam eu pe tata colorând forme ciudate la plajă.
Clasele I – VIII
Cu multe amintiri de la orele de matematică din şcoală nu prea mă pot lăuda. Bănuiesc că eram un copil normal, făra un interes ieşit din comun pentru aceasta disciplină. Există totuşi câteva momente ce merită evocate, mai ales din prisma moralei acelor experienţe. Ca profesor încerc să mă privesc pe mine, cel din copilărie, pentru a-i înţelege pe elevii cu care am de-a face actualmente şi să trag învătăminte corespunzătoare despre ce şi cum trebuie predat.
Din clasele primare nu am nici o amintire legată de aritmetica. În general, din şcoala primară, de la ore, am foarte puţine amintiri. Pun această realitate pe seama faptului ca am urmat primii opt ani la clasă cu predare in limba germană, într-o clasă plină de saşi, eu necunoscând germana din familie. Primele ore de germană le-am avut de-abia pe la cinci ani, iar la şcoala am mers la şase ani. În familie nu vorbeam germană, decât cu bunicul meu cu care mă întălneam de câteva ori pe an. Bănuiesc deci că nu prea înţelegeam mare lucru, decât intuitiv, din tot ce se întâmpla în jurul meu. Am evocat acest pasaj prin prisma importanţei limbii germane în înţelegerea matematicii, aşa cum am trăit-o eu. În această limbă noţiunile sunt pur şi simplu mai clare decât în română. Aş da un singur exemplu în acest moment. Denumirea nemţească pentru bisectoare este Winkelhalbierende care, tradus mot-a-mot înseamnă înjumătăţitoarea de unghi. Micul neamţ nu are nevoie de definiţie pentru această noţiune. Trebuie doar să se confrunte o dată cu ea, să audă o dată cuvântul, şi o ştie. Oricând va reîntâlni într-o problemă cuvântul Winkelhalbierende, va şti despre ce este vorba. Este foarte simplu, chiar dacă sună complicat.
De fapt, prin structura sa, limba germană are multe elemente favorabile gândirii matematice. De pildă, soţia mea a remarcat de curând următorul exemplu, în care pur şi simplu se dă factor comun într-un text de prezentare a unui pateu de porc: unsere Wurstwaren sind allergen-, laktose- und glutenfrei, în loc de allergenfrei, laktosefrei und glutenfrei (cârnaţii noştri sunt liberi de alergeni, lactoză şi gluten). Consider că învăţarea matematicii în limba germană mi-a oferit o claritate mai mare în gândire faţă de nivelul pe care l-aş fi atins dacă aş fi mers la şcoală doar în limba română.
Prima amintire matematică clară din şcoală o am din clasa a cincea, când am mers (am fost trimis) la olimpiadă şi am plecat de acolo năucit, pentru că nu am ştiut nimic. Singurul aspect ce-l ţin minte din timpul lucrării este profunda stare de vinovăţie că nu pot face nimic; un fel de stare ca şi cum aş fi primit aruncată peste mine o găleată cu apă foarte rece, chiar cu bucăţele de gheaţă în ea şi nu înţelegeam ce s-a întâmplat, pentru ce sunt pedepsit. Nici o dată nu am înţeles de ce a trebuit să merg eu atunci la olimpiadă. Probabil pentru că părinţii mei erau profesori de matematică şi se vedea în mine un viitor matematician. A doua zi am aflat că am luat nota 4 şi iar nu am înţeles mare lucru: eu nu scrisesem mai nimic: de unde erau cele trei puncte? Ca adult, corectând la olimpiade, am aflat de unde şi cum se scot acele puncte fără bază în lucrare. Oricum părinţii mei au fost la înălţimea momentului. Nu ţin minte nici un fel de mustrare din partea lor. Dar nici pe la olimpiade nu m-am mai dus până în liceu, când am reuşit câteva calificări la faza judeţeană (dar nimic mai mult).
De-abia în clasa a şasea au luat părinţii măsuri. Cam atunci mi-a pus tatăl meu Gazeta Matematică în mână şi mi-a zis să încerc să fac probleme de acolo. Îmi verifica rezolvările şi îmi arăta cum să le redactez. Încet am început să trimit probleme la Gazeta Matematică şi aşa m-am mai deşteptat cât de cât. Cu mare amărăciune mă gândesc la copiii de azi care nu mai au această ocazie. După ’90 nivelul problemelor propuse în Gazeta Matematică a crescut aşa de mult, încât după o vreme au ajuns total inaccesibile elevului care nu merge la clasă de excelenţă.
Din clasa a şasea încep să am ceva amintiri. Mergeam pe 12 ani – în acei ani copiii mergeau la şcoală după ce împlineau 6 ani. În anii ’80 vârsta de mers la şcoală s-a mutat după 7 ani, existând chiar părinţi care-şi trimiteau copiii de-abia la 8 ani în clasa I.
Din acest an îmi amintesc de regula de trei compusă şi de algoritmul de extragere a rădăcinii pătrate. Ambele le-am ştiut până la teză, după care le-am uitat. Regula de trei compusă nu am fost nevoit să o predau ca profesor, aşa că nici în ziua de azi nu ştiu clar cum era rezolvarea şi ce gândeam acolo. Ţin minte doar nişte săgeţi interesante, dar nu ştiu cum şi de ce le puneam acolo. Problemele respective le rezolv azi prin reducere la unitate – în rarele ocazii când mă mai întâlnesc cu aşa ceva.
Cu radicalii povestea este în schimb mult mai interesantă. Fără să cunosc algoritmul de extragere, pentru că l-am uitat, m-am descurcat mulţumitor până la terminarea facultăţii. Se pare că acesta era fenomenul general. În acest sens îmi aduc aminte de toamna lui ’89 când eram în armată la Bacău. Eram două plutoane de întârziaţi-amânaţi, cu facultatea terminată, mulţi ingineri, câţiva profesori şi câţiva medici, care pierdeam vremea prefăcându-ne că facem armata. Într-o zi a intrat peste noi un maistru militar, bine ameţit de dimineaţă, pus pe harţă şi doritor de a ne arăta cât îi suntem de inferiori. Şi pentru asta ne-a întrebat care mai ştim să calculăm radical din nu-ştiu-ce număr. Doar unul singur a ştiut, şi anume un profesor care apucase să predea un an înainte de a fi convocat la armată. Ştia pentru că apucase să predea lecţia la clasa a şasea. Din ’90 am mers şi eu la catedră. Ştiam toate lecţiile intuitiv. Doar la rădăcina pătrată a trebuit să mă uit timp de patru ani în manual pentru a-mi reaminti în fiecare an paşii; de-abia în al cincelea an am putut preda algoritmul de extragere fără să mă mai uit în manual. Consider că aceasta ridică semne serioase de întrebare asupra felului în care se predă lecţia respectivă în şcoli.
O amintire specială o am de la sfârşitul clasei a şasea. În vacanţa de vară eram cu părinţii la ţară, la bunicii din partea mamei. Tata a luat cu noi culegerea Gheba (aveam un exemplar în limba germană) din care mi-a dat să rezolv exerciţii cu toate operaţiile cu fracţii, cu paranteze şi cu fracţii supraetajate (mai târziu, ca profesor, le alintam cu drag drept tancuri, vapoare, tir-uri etc.). În prima zi am primit de făcut trei exerciţii şi curănd eram gată cu ele şi mă pregăteam să ies la joacă cu verişorii mei şi cu ceilalţi copii de pe uliţă. Tata m-a întors din drum să-i arăt ce-am făcut. Şi nu i-a fost greu să vadă că rezultatele mele nu coincideau cu cele din carte. În culegerile profesorului Gheba exerciţiile de aritmetică şi cele de algebră aveau răspunsul scris lângă exerciţiu. Tata şi-a luat tacticos o carte, s-a aşezat la masă lângă mine şi m-a pus să le mai fac odată. Eram disperat! Toţi se jucau afară, numai eu eram blocat în casă cu exerciţiile acelea stupide. Aşa că am făcut cel mai natural lucru: am socotit o vreme reducând exerciţiul, până spre final, când am schimbat numerele astfel încât să iasă rezultatul din carte. La sfârşit Tata mi-a verificat mulţumit rezultatele, iar eu am avut voie să ies afară la joacă. Nici acum nu ştiu câte exerciţii am rezolvat atunci în acest fel, şi când am început să obţin într-adevăr rezultatele din carte. Interesant este însă că nu am avut nici o dată probleme la operarea cu fracţii. Oare când le-am înţeles cu adevărat? Nu îmi amintesc.
Am continuat să am rezultate mediocre şi în clasa a şaptea, rar urcând peste nota 8. Totuşi se pare că lecţiile le-am prins foarte bine. Am spus mai devreme că, la catedră am predat în general lecţiile fără să le pregătesc dinainte. Mult mai târziu, uitându-mă prin manuale vechi, de pe vremea când eram în gimnaziu, am observat că felul cum predau coincide în multe cazuri cu lecţiile primite în copilărie.
Există însă o amintire, probabil de la această vârstă, a unui prieten drag. Acesta a primit la clasă de găsit (cu rigla şi compasul) centrul unui cerc desenat anterior (de exemplu trasat cu ajutorul unui pahar). Gândirea profesorului merge de obicei spre o construcţie bazată pe alegerea a două coarde neparalele (eventual cu un capăt comun – deci două laturi ale unui triunghi înscris în cerc) şi construirea mediatoarelor acestor coarde. Centrul cercului este situat la intersecţia celor două mediatoare. Prietenul meu a plecat de la o singură coardă. Mediatoarea acesteia este axă de simetrie a cercului, deci diametru, iar centrul cercului se află la mijlocul său (toate acestea erau considerate pe vremea respectivă construcţii geometrice elementare). Profesoara nu a fost capabilă să accepte această rezolvare diferită de a sa, s-au luat la ceartă şi prietenul meu prea impulsiv era cât-pe-aci să se aleagă cu un 4 în catalog.
De-abia în clasa a opta am început să iau la lucrări regulat note peste 8. Probabil datorită faptului că din acest an au început părinţii mei să facă sistematic matematică cu mine. În acest sens au rămas în memoria familiei desele mele gafe lingvistice de începător (reamintesc că la şcoală învăţam în germană, dar cu părinţii mei lucram în română). Mama şi acum se distrează când îşi aduce aminte de linia mijlocică.
Am însă două-trei amintiri deosebite din ultimul an de gimnaziu. Nu ţin minte cum a fost la oră, dar ştiu că după teorema celor trei perpendiculare (T3⊥) am confecţionat acasă o machetă mică din sârmă la care planul era făcut dintr-o bucată de la o cutie de chibrituri. Tata s-a arătat entuziasmat iar macheta respectivă a ajuns în bradul de Crăciun (mulţi ani de atunci a avut locul ei rezervat în brad).
Ţin însă minte foarte bine ora în care s-a calculat la tablă aria laterală a conului (şi apoi curând cea a trunchiului de con). Felul în care s-a desfăşurat suprafaţa laterală a conului, iar apoi aceasta a fost tăiată în felii foarte subţiri, sectoare de cerc aproximate ca triunghiuri isoscele foarte înguste cu înălţimea cam de-aceaşi lungime cu laturile oblice, deci egale cu raza, acest proces m-a impresionat profund. Iar calculul algebric cu descrierea numărului oricât de mare de triunghiuri/sectoare prin folosirea … (puncte-puncte – lor) la sfârşitul sumei, cât şi factorul comun din timpul calculului au pus capacul. În acestă demonstraţie mi s-au legat brusc toate cele predate în cei patru ani de către profesorul meu, Dl. Willhelm Schotch (se pronunţă Şoci). Datorită acestei lecţii, după ce am ajuns la rândul meu profesor, am constatat că dânsul era modelul meu cel mai important. În orice lecţie încerc să-l imit, străduindu-mă să trezesc în elevi fascinaţia trăită de mine ca elev în acea oră. Faptul că în curând a venit şi aria laterală a trunchiului de con, demonstrată prin aceeaşi metodă, dar împărţind suprafaţa desfăşurată în foarte subţiri trapeze, m-a ajutat şi mai mult să ţin minte metoda. Da, tot jocul acela algebric cu sume nesfârşite de fracţii şi factori comuni se potrivea şi în cazul unor trapeze, creând asupra mea impresii de neşters.
Scurt după această lecţie au venit corpurile de rotaţie. Mulţi oameni îşi aduc aminte cu plăcere de problemele din această lecţie, care din păcate de ani buni nu mai este în programă. Este vorba de probleme de tipul un triunghi dreptunghic cu laturile date se roteşte pe rând în jurul fiecărei laturi. Calculaţi aria şi volumul corpurilor astfel formate. Fără a fi banale, aceste probleme oferă rezolvitorului ocazia de a-şi exersa aptitudini aritmetice şi matematice elementare uşor de asamblat într-o rezolvare completă. Cu alte cuvinte, aceste probleme atrag elevii obişnuiţi către matematică, oferindu-le astfel ocazia de a avea satisfacţie şi de pe urma matematicii.
La această lecţie existau în unele şcoli aparate cu un motor în care se fixau ca într-un mixer sau o maşină de găurit nişte tije de care erau ataşate figuri geometrice din tablă. Odată ce se roteau cu mare viteză, se putea vedea uşor corpul de rotaţie generat. Era astfel ajutată imaginaţia copiilor în înţelegerea acestor probleme. Profesorul nostru nu avea un astfel de aparat la şcoală, aşa că m-am oferit să aduc unul de la liceu, de la laboratorul de matematică al părinţilor mei. Nu ştiu cât de mult i-a ajutat pe colegii mei, dar mie mi-a oferit o experienţă colaterală memorabilă.
Ştiind că aparatul este greu, am cerut să vină un coleg cu mine şi l-am ales pe colegul care era cel mai tare în clasă la matematică. Pe drum către liceu am început un joc. La rând alegeam o formulă de arie sau volum şi vedeam care o zice primul corect. Colegul respectiv le învăţase pe-de-rost, pe când eu m-i le deduceam fiecare în cap. Una din cinci le nimerea el mai repede corect. La celelalte zicea el înaintea mea, dar eu îi demonstram imediat de ce nu are dreptate şi care este formula corectă. Această mică lecţie de viaţă mi-a arătat că pot să mă bazez mult mai bine pe judecată decât pe memorie. Şi acum, ca profesor, nu le dau elevilor formulele, ci le cer să le deducă pe rând, iar eu doar le scriu pe tablă. Cei care intră în acest joc şi acceptă să gândească nu le vor mai uita nici odată. Există doar câteva formule care trebuie învăţate pe-de-rost pentru că nu pot fi deduse accesibil în minte (înălţimea în tetraedrul regulat sau volumul acestuia sunt greu de dedus în cap; la formulele sferei, eu le ofer elevilor pseudo-deduceri, care sunt însă accesibile în minte: Arhimede a arătat că aria sferei este de patru ori aria cercului etc.).
Legat de aparatul respectiv de rotit figuri, trebuie să precizez că aş fi putut să-mi fac de multe ori şi eu unul, ca profesor: dintr-un mixer vechi, sau pe baza unei maşini de găurit cu piesele de prins uşor în mandrină. Dar, NU! Eu am preferat să le povestesc elevilor de fiecare dată întâmplarea din copilărie şi să le prezint fenomenul corpurilor de rotaţie în imaginaţie. Consider că este mult mai bine să le folosim şi să le antrenăm elevilor cât mai des imaginaţia. Orice matematician care îşi analizează cum îi gândeşte mintea va recunoaşte importanţa deosebită a unei imaginaţii bine dezvoltate.
Cam acestea ar fi tot ce ţin minte din gimnaziu şi merită a fi evocat într-o discuţie despre matematică. Totuşi, ar mai fi două-trei momente ce ar trebui amintite.
Primul ar fi o întâlnire specială. Părinţii mei au organizat în aceşti ani un simpozion naţional de matematică. Cu ocazia respectivă l-am cunoscut pe Academicianul Nicolae Teodorescu, preşedintele din acea vreme a SSM (Societăţii de Ştiinţe Matematice din România). Mare lucru nu am înţeles atunci din acea întâlnire, dar mi-a oferit de-a lungul anilor un motiv de mândrie: avusesem în copilărie o întâlnire cu unul dintre marii matematicieni ai ţării.
A doua întâmplare deosebită nu este legată direct de matematică, dar merită totuşi amintită. Tata îşi pusese în minte să construiască în Victoria un observator astronomic, sub tutela unui alt academician, Profesorul Gheorghe Chiş de la Universitatea din Cluj. Totul mergea bine, se achiziţionase un telescop cu oglinda de 20 cm, pe inventarul liceului unde era tata titular, se lucra la amenajarea unui vechi turn de apă şi ultimele amintiri le am că lucrau cu un inginer la proiectarea roţii dinţate pe care urma să se rotească cupola observatorului. Apoi a picat vestea cea grea: Profesorul Chiş a murit neaşteptat. Din acel moment s-au năpustit “şacalii”: diferiţi indivizi suspuşi din oraş au început să cârcotească şi să reclame că din observator, cu ajutorul telescopului se va putea spiona în combinatul chimic unde erau obiective de nivel strategic. Aşa că foarte repede proiectul a fost îngropat şi nici o dată nu s-a mai repornit. Acel telescop nu a fost folosit nici o dată şi s-a distrus prin oxidare datorită neîntreţinerii.
Şi pe domnul academician Gheorghe Chiş îl ţin minte; l-am cunoscut când a fost în vizită acasă la părinţii mei. Peste ani am aflat că şi un verişor de-al bunicului meu este academician: Profesorul Radu Grigorovici.
Al treilea moment special demn de amintit ar fi următorul. Pe vremea respectivă exista o emisiune la televizor, Teleşcoala, ce era difuzată înainte-de-masa şi în care erau prezentate diferite lecţii. Concret câte o profesoară stătea la tablă şi explica lecţia în timp ce era filmată. Prin această emisiune ministerul se ocupa de perfecţionarea dascălilor. Totodată aici erau prezentate noile lecţii introduse în programă.
În cadrul reformei şcolare de la sfârşitul anilor 70 a fost introdusă, la început în liceu, noţiunea de congruenţă. Pentru exemplificarea pe Congruenţa triunghiurilor la teleşcoala a fost aleasă de către realizatorul TVR tocmai mama mea (domnul respectiv se rătăcise prin Victoria şi aşa s-au întâlnit). Ca urmare am ajuns să o văd şi pe mama la televizor! Atunci, în 1980, la televizor n-am înţeles mare lucru – noi în gimnaziu foloseam noţiunea de egalitate – dar am avut ocazia să revăd lecţia respectivă pe viu în liceu, cu mama ca profesoară de matematică la catedră.
Ca profesor m-am confruntat peste ani puternic cu acest subiect. Noi învăţasem geometria din gimnaziu în limbajul vechi: două segmente erau egale, lecţia respectivă se numea Cazurile de egalitate a triunghiurilor, unghiurile – cu acoperiş deasupra – nu aveau măsură, ci erau egale cu 45o, iar despre axiome mare lucru nu ştiam. În schimb, majorităţii elevilor ne plăcea geometria! Când am reluat-o în liceu, în clasa a IX-a, nu am avut nici o problemă să trecem la scrierea nouă, mult mai riguroasă, cu congruenţă şi măsura unghiurilor. Cu axiomele însă, ţin minte că ne luptam şi ca profesori, pe vremea examenului de definitivat.
Când am ajuns profesor, elevii trebuiau să folosească direct scrierea riguroasă, iar eu având o empatie mai dezvoltată simţeam puternic chinul lor de-a înţelege de-odată o materie nouă şi un limbaj prea încărcat, despre care ştiam că este artificial încărcat.
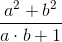este pătratul unui număr întreg. În textul original observăm că se foloseşte denumirea întreg pozitiv pentru număr natural.