Category: Metodică

În partea a doua a acestei serii am prezentat o formă diferită de introducere a numerelor prime în clasa a V-a, faţă de ceea ce se practică la ora actuală.. Forma de predare riguroasă, cu care suntem obişnuiţi majoritatea profesorilor, ne cere să dăm o definiţie unică, pe baza căreia apoi să deducem eventual alte aspecte ale obiectului matematic studiat, într-un sistem de observaţii şi teoreme. Aşa suntem învăţaţi şi obişnuiţi toţi profesorii (noblesse oblige!), şi cu greu acceptăm o altă cale de abordare a lucrurilor. Merită aşadar, să privim cu mai multă atenţie asupra gândurilor ce au stat în spatele unei abordări atăt de profund diferite, ca cea din postarea precedentă, pentru a nu lăsa cititorul într-o profundă stare de nedumerire.

Principiul de bază urmărit prin această abordare, este acela că orice noţiune nouă trebuie adusă la cunoştinţă elevilor prin cât mai multe abordări diferite, nu doar printr-una, surprinzând astfel într-o formă naturală exact ce se întâmplă atunci când vedem un obiect nou, nemaiîntâlnit: îl luăm în mână şi îl întoarcem “pe toate feţele”, analizându-l cu atenţie şi descoperindu-i încet diferite detalii. Acest principiu este total opus principiului doct folosit în prezentarea riguroasă, de sorginte academică, a noţiunilor matematice prin intermediul definiţiei (a unei unice şi a-tot-dominatoare definiţii). Mai ales la clasele mici consider că  principiul predării prin unice şi seci definiţii este total nepotrivit, această cale reprezentând una din sursele eşecului în învăţarea matematicii la mulţi elevi. Apropierea de o noţiune esenţială, cum sunt numerele prime, cu calm, paşnic, azi dintr-o parte, mâine din altă parte, săptămâna viitoare iarăşi dintr-o altă parte, le poate oferi şi elevilor normali şansa de a pricepe până la urmă ce vrea noua noţiune.

La proaspătul elev de clasa a V-a, în semestrul I, această apropiere de numerele prime trebuie făcută cu blăndeţe, aproape ca într-o poveste. Dacă eu nu am reuşit să prezint destul de convingător această nuanţă a predării, permiteţi-mi să îl chem în ajutor pe marele Euler, prezentându-vă felul cum acesta se apropia de subiectul numerelor prime. În finalul lui 2016 am achiziţionat dintr-un anticariat virtual o mică comoară, cartea Vollständige Anleitung zur Algebra von Leonhard Euler  (Introducere completă în/către Algebră de Leonhard Euler). Permiteţi-mi să vă traduc în acest sens câteva pasaje din Capitolul 4 al primei părţi a acestei cărţi (pag. 25-27):

37. Am observat, că un produs este compus din două sau mai multe numere care se înmulţesc între ele, acestea numindu-se factori. …
38. Dacă analizăm toate numerele, în ce măsură acestea se pot obţine prin înmulţire a două sau mai multe numere, atunci vom constata destul de repede că unele nici nu se pot obţine prin înmulţire, şi astfel nu au deloc factori; altele însă se pot scrie înmulţit cu două sau mai multe numere, ca urmare având doi sau mai mulţi factori.

Astfel, 4 dă căt 2∙2, mai departe 6 dă cât 2∙3, apoi 8 dă căt 2∙2∙2 …

39. Dimpotrivă, numerele 2, 3, 5, 7, 11, 13, 17 etc. nu se lasă descompuse în acelaşi fel în factori, doar dacă nu l-am lua în ajutor şi pe 1, astfel încât de exemplu pe 2 să-l reprezentăm ca 1∙2. Dar, datorită faptului că un număr înmulţit cu 1 nu se modifică, atunci pe 1 nici nu-l putem privi ca factor.

Toate aceste numere care nu se pot descompune în factori, ca 2, 3, 5, 7, 11, 13, 17 etc., se numesc numere simple sau numere prime; toate numerele rămase însă, cele care se pot reprezenta cu factori, adică 4, 6, 8, 9, 10, 12, 14, 15, 16, 18 etc., se numesc numere compuse. …

41. Numerele compuse însă, cele care se lasă prezentate prin factori, izvoresc toate din numerele prime de mai sus, astfel încât toţi factorii sunt numere prime. Pentru că dacă un factor nu ar fi număr prim, ci un număr compus, atunci acesta s-ar putea la rândul său descompune în doi sau mai mulţi factori numere prime. Deci, dacă numărul 30 se reprezintă prin 5∙6, iar 6 nu este număr prim, ci 2∙3, aşadar 30 se poate reprezenta prin 5∙2∙3 sau prin 2∙3∙5, toţi factorii fiind numere prime. …(urmează câteva exemple de descompunere, inclusiv descompunerea lui 360, extrăgând din acesta câte un factor de 2, apoi câte un factor de 3 etc., ceva de genul 360 = 2∙180, iar 180 = 2∙90 ş.a.m.d.)

Ca urmare, numărul 360 se descompune în factori simpli ca: 2∙2∙2∙3∙3∙5, care numere, toate înmulţite dau ca rezultat 360.

44. Vedem din acestea că numerele prime nu se pot împărţi prin alte numere, pe când numerele compuse cel mai des se pot descompune în factorii lor simpli, căutând toate numerele simple prin care acestea se lasă împărţite. …

Da, aşa vorbea marele Euler despre numerele prime, de parcă totul ar făcea parte dintr-o poveste minunată, în care numerele prime sunt unele din multele personaje. Am convingerea, că această poveste este mult mai potrivită elevilor de clasa a V-a, decât formele practicate actualmente, adaptate după diverse variante de cursuri universitare. Acest prim principiu enunţat mai sus ar putea fi prezentat scurt şi sec şi în felul următor: caracterizare, nu definire!

Un alt principiu foarte important, urmărit în predarea prezentată, este cel enunţat de către un prieten, Zan Redzic, profesor din Germania, sub titlul de Spieldrang = impulsul de a te juca; dorinţa de joc. Într-adevăr, elevii au un impuls nestăvilit de a se juca, de a transforma cu bucurie orice activitate în joc. Astfel, după cum aţi putut observa, prima apariţie a numerelor prime am făcut-o adus-o exact printr-un “joc”. Chiar şi numai pronunţarea cuvântului “joc” detensionează foarte mult starea sufletească a unor elevi mai fricoşi în ceea ce priveşte matematica.

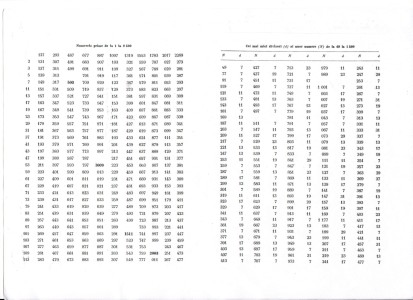
Astfel, de la o vreme, chiar “vânarea” numerelor prime devine un joc în sine, cu fiecare oră de matematică lărgindu-se experienţa elevilor în localizarea unor noi numere prime. Desigur că elevii trebuie ajutaţi în această vânătoare; de pildă, într-una din orele următoare Ciurului lui Eratostene le aduc elevilor o coală de hârtie în formatul A5 având pe o parte toate numerele prime până la 2500, iar pe cealaltă un tabel cu cei mai mici divizori ai unor numere până la 1500 (fotocopiată din Ioan Şt. Muşat, C. Ionescu Ţiu, Exerciţii şi probleme de matematică pentru concursul de admitere în licee, Ed. didactică şi pedagogică, 1971, Biblioteca S.S.M. din R.S.R., pag. 15,16; vezi anexa la prezentul eseu; imprimaţi pe format A4 pe ambele părţi şi tăiaţi în două A5). Cu ajutorul acestora elevii pot vâna mult mai “profesionist” numere prime dincolo de limita învăţării intuitive (până pe la 30-40), dincolo de limita probei împărţirii în cap (cam până la 100) şi dincolo de limita propriului Ciur al lui Eratostene (numerele prime până pe la 250). Iar dacă un număr nu este pe lista cu numere prime, elevul poate înţelege cum se face descompunerea acestuia, în cazul când nu se împarte exact cu 2, 5, sau 3. Descompunerea unor astfel de numere devine aici un joc în sine.

Un nou joc, care nu ţine aparent de numerele prime, este scrierea primilor termeni din şirurile de puteri cunoscute, ale lui 2 (până la 2¹²), lui 3 (până la 3¹⁰), lui 4 (până la 4⁶), lui 5 (până la 5⁸) sau ale lui 10 (foarte distractiv, merge până la 10¹⁰). După ce s-au obişnuit cu acestea, le putem prezenta elevilor două tipuri de numere cu totul speciale, ce au reprezentat momente majore în evoluţia matematicii: Numerele lui Mersenne şi Numerele lui Fermat, care au reprezentat în viziunea autorilor tentative de găsit a unor reguli ce ar genera numere prime. Pentru noi, fiecare din aceste şiruri reprezintă un joc în care elevii pot urmări dacă anumite numere sunt sau nu numere prime.

Numerele lui Mersenne (Călugărul Marin Mersenne, 1588-1648), calculate cu formula M_n = 2ⁿ – 1, reprezintă o primă încercare de găsire a unei reţete pentru obţinerea de numere prime. Încercarea nu a fost una de mare succes, dar aceasta reprezintă o poveste interesantă şi baza pentru un mic joc în care elevii să verifice care sunt numere prime şi care nu sunt. Totodată elevii au reuşit să observe şi alte legităţi legate de ultima cifră, legităţi ce sunt conectate cu cele mult mai cunoscute legate de evoluţia ultimei cifre la şirurile puterilor. Despre Mersenne le povestesc elevilor că a reprezentat unul din primele nuclee ştiinţifice ale vremii, întreţinând o corespondenţă activă cu mai-marii vremii: Descartes, Galilei, Pascal etc. grupul din jurul său reprezentând nucleul pe urma căruia s-a înfiinţat Academia franceză. Cu elevii am verificat primele 12 numere ale lui Mersenne, pentru n de la 1 la 12. Astfel se numere prime doar pentru n = 2, 3, 5, 7; Următorul prim se obţine pentru n = 13 şi verificarea acestuia reprezintă deja o sarcină doar pentru elevii pasionaţi de matematică (temă neobligatorie). Numărul 8191, cunoscut ca “primul lui Mersenne”, poate fi sursa unor preocupări interesante pentru elevii buni de clasa a V-a (vezi Apostolos Doxiadis – Unchiul Petros şi Conjectura lui Goldbach, Ed. HUMANITAS, 2003, pag. 125). Las cititorului bucuria de a găsi şi alte surse despre aceste numere fascinante.

Numerele lui Fermat (Pierre de Fermat, 1607-1665) au reprezentat o încercare mult mai reuşită de a găsi o reţetă pentru obţinerea unor numere prime. Faptul că 257 este prim se constată din tabel; verificarea lui 65537 (numărul lui Fermat pentru n = 4) este însă un exerciţiu puternic şi pentru elevii buni la matematică. Povestea interesantă însă, de-abia acum începe: următorul număr Fermat, pentru n = 5, este 4.294.967.297, iar despre acesta s-a presupus că este tot număr prim. Marele Fermat trebuie că avusese dreptate. De-abia în 1732, Leonhard Euler a arătat că 4.294.967.297 = 641 ∙ 6.700.417 şi deci că nu este prim, spulberând astfel marele mit al numerelor prime ale lui Fermat. În era computerelor, în 1966, s-a arătat că următoarele 38 de numere Fermat sunt toate compuse. Aceasta rămâne însă o foarte frumoasă poveste de spus la ora de matematică.

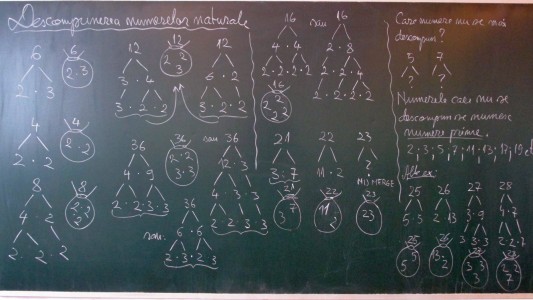
Dacă tot vorbirăm de jocuri cu numere prime, în ultimii doi ani am exersat cu elevii o formă interesantă de găsire a tuturor divizorilor unui număr natural, bazată pe descompunerea acestuia în factori primi. Astfel, am aranjat divizorii într-un fel de tabel organizat pe nivele după numărul de factori primi care sunt asamblaţi pentru a obţine divizorii. Cu metoda respectivă se pot găsi cu mare siguranţă toţi divizorii, pe baza faptului că tabelul respectiv în formă de frunză are formă simetrică, nivelele simetrice faţă de extremităţi având un număr egal de divizori. Poza următoare a tablei din ora respectivă arată două cazuri mai simple, D₁₂ şi D₇₂, din care puteţi deduce “regulile acestui joc”. Vă propun în continuare să vă distraţi cu găsirea tuturor divizorilor unui număr ceva mai mare, numărul 3000, care are descompunerea în şapte factori de trei feluri, tabelul pe opt nivele oferind în mod ordonat toţi cei 32 de divizori.

Merită făcută aici o scurtă comparaţie legată de accesibilitatea în ceea ce priveşte posibilitatea de înţelegere de către elevi a acestei abordări vizavi de tot mai frecventata formulă care ne dă direct numărul divizorilor unui număr. De pildă 3000 = 3¹∙2³∙5³ are un număr de (1+1)∙(3+1)∙(3+1) = 2∙4∙4 = 32 divizori. Aceasta se aplică foarte repede, dar elevul nu înţelege nimic, efectul fiind acela de cutie neagră. Dimpotrivă, la găsirea tuturor divizorilor prin metoda prezentată mai sus cu tabelul în formă de frunză, se lucrează foarte mult, dar elevii înţeleg fiecare pas şi pricep despre ce-i vorba; doar capacitatea lor limitată de atenţie şi de concentrare le poate sta în cale în înţelegerea fenomenului. Oare, după care din cele două elevii – mai ales cei buni – şi gândirea lor matematică rămân mai câştigaţi?

În prezentarea apariţiei numerelor prime am atins – doar tangenţial – un principiu important, anume acela de a studia un subiect începând cu metode primitive, şi ajungând în final la metoda generală, mai elaborată din punct de vedere teoretic. Concret, am abordat descompunerea numerelor naturale în factori primi într-o formă lejeră, intuitivă, liberă, bazată doar pe amintiri din tabla înmulţirii. De-abia apoi (în cazul de faţă, doar ora următoare) am dedus din aceasta metoda descompunerii în factori primi cu linia verticală, prin împărţiri succesive la numerele prime 2 şi 5, apoi 3, 7 sau 11. Pentru a ajunge la ideea de împărţire, după prima oră a trebuit să supun discuţiei în plenul clasei următoarea dublă întrebare: ce operaţie este când în “săculeţul” cu factori primi ai unui număr mai pun un nou factor, respectiv ce operaţie aritmetică are loc atunci când “scot din săculeţ” un factor? De-abia după conştientizarea faptului că extragerea unui factor înseamnă de fapt împărţirea numărului cu acel factor, de-abia după aceasta am putut transforma în câţiva paşi prima metodă de descompunere în metoda cunoscută de toată lumea. În toate orele următoare am folosit însă alternativ, după cum se potrivea mai bine, prima sau a doua dintre metode.

Acest ultim principiu prezentat este însă foarte înrudit – aproape pănă la confundare – cu un altul, anume acela de a începe învăţarea unei teme de la cazuri particulare, rezolvabile în minte, şi a evolua, ajungând cât mai târziu la cazuri dificile, rezolvabile doar prin metode scrise, mai exact prin algoritmi. De pildă, numărul 81 se poate descompune mintal prin prima metodă foarte simplu, descompunând în faza intermediară 81 în 9∙9, iar apoi fiecare 9 în 3∙3, obţinând deci 81 = 3∙3∙3∙3. Este evident că această descompunere este mult mai uşoară decât cea bazată pe împărţirea 81:3 = 27. De-abia la a doua metodă de descompunere a apărut şi artificiul de calcul de împărţire la 2∙5 în cazul descompunerii numerelor cu zero la ultima cifră.

Ca o paranteză fie spus, la exerciţiile de descompunere a numerelor în factori primi, la exemplele tot mai complicate, se potriveşte de minune a aduce în discuţie ideea de putere a numerelor naturale, la început ca o simplă metodă de scurtare a scrierii. Anul acesta, când mă pregăteam ca ora viitoare să supun discuţiei ideea unei scrieri mai scurte, doi elevi au sărit în sus, că asta trebuie să fie operaţia de putere! (o văzuseră la un verişor sau un frate mai mare).

Există şi un principiu mai rar folosit, care însă ajută foarte mult la studiul unor situaţii numerice. Este vorba de încercarea de a arăta conexiunile numerice prin anumite conexiuni sau ordonări grafice. Probabil, cel mai cunoscut exemplu este acela când calculăm o Sumă Gauss fără formulă, adunănd primul termen cu ultimul, al doilea cu penultimul ş.a.m.d., conectând perechile de termeni adunaţi pe hârtie cu câte o linie curbă. Evidenţierea grafică a unor conexiuni poate contribui la formarea unei viziuni mai clare asupra sistemului de relaţii între elementele studiate (citat relativ din George Polya, Descoperirea în matematică, Ed. Ştiinţifică, 1971, pag 178, pr. 6.20). Evidenţierea grafică a unor astfel de conexiuni între elementele studiate poate ajuta foarte mult la înţelegerea şi clarificarea conexiunilor dintre numerele participante în momentul respectiv. Aceste încercări de evidenţiere a conexiunilor apar în două locuri în lecţiile prezentate. În primul rând s-a văzut la descompunerea numerelor în factori, unde am prezentat descompunerea în forma unui graf pe care elevii îl denumesc după libera inspiraţie (brăduleţ, triunghi sau piramidă, reţea de rădăcini etc.) Un al doilea loc de amintit a fost forma în care se pot organiza divizorii unui număr, după numărul factorilor primi ce intră în componenţa fiecărui divizor. Acele tabele în formă de frunză oferă elevilor o structură ce reprezintă de fapt o schelă de susţinere a gândurilor necesare pentru atingerea obiectivului propus.

Să analizăm în final şi un alt aspect, mai special, despre prezentarea la clasă a acestui material. Poate v-aţi întrebat de ce nu am folosit deloc expresii şi scriere specifice teoriei mulţimilor. Puteam desigur să le folosesc, dar nu a fost neapărat nevoie. Mai precis, am vrut să arat că se poate studia liniştit această temă fără limbajul mulţimilor, care la început doar îi încurcă pe elevi. Scrierea în limbajul mulţimilor a fost introdusă în clasele gimnaziale de-abia odată cu reforma din 1980, contribuind din plin la îngreunarea materiei şi la percepţia generală că matematica este o materie grea ce nu prea se poate înţelege, fiind scrisă într-un mod mult prea ştiinţific, inteligibil doar pentru “micii Einsteini”. Trebuie să înţelegem, însă, că limbajul mulţimilor nu a fost folosit nici la nivel înalt decât în ultima parte a secolului XX. De pildă, în lucrarea Ce ştim şi ce nu ştim despre numerele prime a profesorului Waclaw Sierpinski (Ed. Ştiinţifică, 1966), acesta se descurcă de minune fără a folosi nici măcar o dată elemente de scriere din limbajul mulţimilor (lucrarea este tradusă după Waclaw Sierpinski, A selection of problems in the theory of numbers, Pergamon Press, Oxford ∙ London ∙ New York ∙ Paris, 1964).

Aici este ascuns un alt principiu didactic deseori neglijat în predarea matematicii, anume faptul că orice lucru nou trebuie oferit elevilor într-o ambianţă familiară cunoscută, pe un fundament deja stabilizat pe o lungă perioadă de timp, adică într-un limbaj bine cunoscut şi stăpânit de toţi elevii. A introduce noţiuni noi folosind totodată un limbaj de tip nou (introdus la repezeală cu câteva ore în urmă) este o gafă de proporţii, ce se repetă în multe alte puncte ale predării matematicii, această metodă fiind impusă în predarea din România de-abia odată cu Reforma uitată din 1980 (reforma, din păcate, de mult uitată de către majoritatea profesorilor).

6 Ian. 2017

Titus Grigorovici

Chiar dacă folosim deseori expresia Arta predării matematicii, oare ne este clar despre ce vorbim, oare ce înţeleg alţi profesori din aceasta? De curând am găsit în revista NATIONAL GEOGRAPHIC TRAVELER (Vol. 21, Iulie-August 2014, pag. 64-74) un articol deosebit despre artiştii artizani din Italia: Made in Italy, articol în care sunt prezentaţi meşteşugari din Murano, Napoli, Milano şi alte astfel de locuri minunate.

Găsim în acest articol citate remarcabile despre principiile care-i însufleţesc pe aceştia: Made în Italy înseamnă produse făcute cu suflet (pag. 64). De exemplu, la Bologna găsim … atelierul Peron & Peron, care produce manual, cu grijă, pantofi pe comandă – cam o mie de perechi pe an, …”Pasiunea pentru meşteşug e în AND-ul nostru”, spune Simone Peron. “Vizităm clientul acasă, încercăm să-l cunoaştem, să-i observăm stilul vestimentar, mobila. Trebuie să fim atât buni artizani, cât şi buni psihologi.” În mod similar se vorbeşte şi despre pălărierul Gianni Gatto, mai exact sculptor de pălării din Florenţa, în prezentarea  Nu doar o pălărie, ci artă de purtat în cap:… Ajută şi faptul că Gatto ţine cont de persoana pentru care crează fiecare pălărie. “Pălăria singură e incompletă”, spune el. “Omul o întregeşte, purtând-o într-un fel anume, dându-i suflet şi personalitate.”(pag. 73)

În mod similar profesorul de matematică trebuie să fie un artist al predării: să îmbine atenţia pentru client – elevul, fiecare elev – cu atenţia pentru gândirea matematică – gândirea adaptată fiecărei vârste şcolare. Predarea trebuie făcută cu suflet; pasiunea pentru meşteşug, pentru meşteşugul predării matematicii, trebuie să fie în ADN-ul nostru. Trebuie să fim atât buni matematicieni, cât şi buni psihologi. Profesorul de matematică trebuie să fie sculptor de gândire. Nu doar matematică ci gândire vie de purtat şi folosit o viaţă. Ajută faptul că profesorul ţine cont de persoana (elevul) pentru care crează sau alege fiecare problemă. O problemă singură e incompletă. Elevul o întregeşte, primind-o într-un fel anume, dându-i suflet şi personalitate, prin felul cum reacţionează la aceasta, cum o rezolvă, ce gânduri generază când îi caută soluţia.

Leonardo da Matematici

Numerele prime reprezintă atomii, părţile componente din care sunt create multiplicativ toate celelalte numere. A reduce aceste minuni matematice la o simplă şi unică definiţie este tot ce poate fi făcut mai rău minţii tinere şi proaspete a elevului de clasa a V-a. Acesta, doritor de a afla cât mai multe lucruri frumoase de la profesorul de matematică, este “lovit” cu o definiţie unilaterală, ce surprinde doar o singură faţetă a acestor nestemate matematice. În urma unei astfel de predări, cei mai mulţi nu ajung să le înţeleagă, se sperie de ele şi de orice apariţie a acestora, ca de nişte ciudate bestii cu care cel mai bine să nu ai de-a face; le asimilează deseori numerelor impare şi se blochează când le vorbeşti de 2 ca număr prim par sau de 9 sau de 15 ca numere impare neprime. Abordarea cunoaşterii intuitive din cât mai multe situaţii poate ajuta mult în prevenirea “ceţii ce se pune pe creierul” multor elevi în ceea ce priveşte numerele prime.

De mulţi ani încerc să găsesc diferite căi de a mă apropia de noţiunea de număr prim într-un mod cât mai natural, potrivit elevului de gimnaziu aflat în proces, undeva între gândirea aritmetică a ciclului primar şi gândirea matematică avansată ce va să vină cu înaintarea în vârstă. La clasa a V-a de anul acesta am reuşit încă un pas important în acest demers, găsind în sfârşit o explicaţie plauzibilă pentru denumirea acestor numere, lămurind astfel care este legătura între numerele prime şi cuvântul “primul”. Cu elevii de anul acesta am reuşit nu mai puţin de şase-şapte abordări mai mult sau mai puţin diferite a noţiunii de număr prim. Iată-le în continuare pe acestea în ordinea în care au apărut în lecţii, dar şi altele ce vor apărea la discuţii ulterioare.

Pasul 1) Prima apariţie a numerelor prime a fost în cadrul unui “joc”, în care ne-am propus să descompunem multiplicativ diverse numere. Abordarea a fost una profund intuitivă, fără nici o cât de mică tentativă de teoretizare prealabilă: pur şi simplu, le-am arătat elevilor câteva exemple, pe marginea cărora am discutat principalele aspecte ale “jocului”: că numărul 1 nu participă pentru că atunci jocul nu s-ar mai termina, că pot exista diferite căi de a descompune un număr, dar că întotdeauna se ajunge la aceeaşi formă finală, descompunerile putând varia doar comutativ, că există numere la care descompunerea este mai stufoasă, mai bogată, dar şi numere mai sărace, iar aceasta nu depinde de mărimea numărului (ce ciudat!); în sfârşit, am constatat că există numere care nu se pot descompune multiplicativ. În acest moment au apărut aproape deodată primele două descrieri ale ideii de număr prim. Numerele din finalul oricărei descompuneri se numesc numere prime; ele sunt un fel de piese de bază din care sunt compuse multiplicativ toate celelalte numere, ca într-un ciudat joc Lego. Astfel, există piese mai mici, de 2, 3 sau 5 unităţi, sau piese mai mari de 7 sau 11 unităţi sau mai multe. Pe de altă parte, numerele prime apar la startul unor “partide”, acele numere la care avem surpriza să constatăm că nu le putem descompune în cadrul acestui “joc”. Da, există şi numere prime mai mari, cum ar fi 13, 17 sau 19. Aici apare prima oară o întrebare ciudată: “mai există şi alte astfel de numere, mai mari?”. După cât mai multe exemple rezolvate în clasă, ca temă, elevii au avut să descompună intuitiv şi restul numerelor până la 100 (cât mai multe; unii le-au descompus pe toate care se puteau, alţii au urcat doar către 50). La recapitularea de la începutul următoarei ore am concluzionat că există două tipuri de numere: numerele prime şi numerele compuse; numerele compuse sunt acelea care se pot descompune în produs, pe când numerele prime nu se pot descompune.

După acest prim contact cu numerele prime am încercat şi o primă listă de contabilizare a acestora, listă care, în funcţie de elev, arăta cam aşa: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, etc. Aspectul comutativităţii înmulţirii numerelor naturale a apărut aici din belşug, şi reprezintă unul din gândurile de unde mi-a venit ideea de a aduna piesele componente ale fiecărui număr descompus într-un săculeţ (adică numerele prime), săculeţ în care acestea se amestecă, necontând la produsul final ordinea în care se reînmulţesc. Lecţiile şi-au urmat apoi cursul către introducerea formei oficiale a descompunerii numerelor naturale, binecunoscuta descompunere “cu bară”. Cuprinse doar pe baza celor înţelese intuitiv la prima lecţie despre descompunerea numerelor naturale, numerele prime au apărut în fiecare din lecţiile următoare, prin simpla folosire tot mai frecventă, chiar dacă noţiunea nu era încă lămurită complet din punct de vedere oficial. De pildă, cu timpul s-a ajuns fără nici un stres la folosirea naturală a expresiei “descompunerea în produs de puteri de factori primi”.

Pasul 1’) Un mic pas înainte, care ţine totuşi de aspectul de descompunere în produs a unui număr, l-am făcut atunci când am încercat un alt “joc”. Astfel, ne-am propus să reprezentăm diferite numere naturale cu punctuleţe în formă dreptunghiulară. Aceste reprezentări pot fi făcute cu punctuleţe aliniate pe hârtie sau cu punctuleţe materiale ordonate pe masă (monede de un ban, boabe de cafea sau de fasole). Ideea apare exploatată din belşug în romanul lui Apostolos Doxiadis – Unchiul Petros şi Conjectura lui Goldbach (Ed. HUMANITAS, 2003) Astfel, la pagina 120, numerele compuse sunt prezentate în formă dreptunghiulară de rânduri şi coloane. De exemplu, numărul 35 are o singură reprezentare posibilă, de 5 rânduri şi 7 coloane, care poate fi însă comutată în 7 rânduri şi 5 coloane (comutativitatea reprezentată vizual). Numărul 24 are trei reprezentări total diferite: 4 ∙ 6, 3 ∙ 8 şi 2 ∙ 12. La unele numere reprezentarea în formă dreptunghiulară apare în forma unui pătrat. Astfel, la numărul 16 avem reprezentarea dreptunghiulară 2 ∙ 8 şi reprezentarea pătrată 4 ∙ 4. Întorcându-ne la tema noastră, observăm că numerele prime nu pot fi reprezentate sub formă de dreptunghiuri complete. În romanul lui Apostolos Doxiadis, Unchiul Petros le reprezenta sub forma unor şiruri de punctuleţe de un rând.

Pasul 2) O nouă apropiere de numerele prime am avut odată cu studierea unor şiruri elementare de numere. Elevii din şcolile Waldorf folosesc din ciclul primar expresii de genul şirul lui 3, cu sensul de şirul multiplilor lui 3, înţelegând prin acestea rezultatele tablei înmulţirii. Aşadar, fără mari complicaţii teoretice, doar intuitiv, am putut enumera câteva şiruri de multipli (multipli = un număr de mai multe ori, clar), pornind de la numărul însuşi. Este foarte important să ne înfrânăm aici să “recităm” lecţia teoretică şi riguros completă (impuls dominant la majoritatea profesorilor), pentru că numărul zero, prezentat de obicei ca primul multiplu, doar încurcă aici lucrurile. Oricum, demersul în această formă este profund corect din punct de vedere istoric: numărul zero a apărut mult mai târziu decât numerele prime. Ca urmare, pe tablă am scris ceva de genul:

M₂: 2, 4, 6, 8, 10, 12, 14, …
M₃: 3, 6, 9, 12, 15, 18, 21, …
M₄: 4, 8, 12, 16, 20, 24, …
M₅: 5, 10, 15, 20, 25, 30, …
M₆: 6, 12, 18, 24, 30, 36, …
M₇: 7, 14, 21, 28, 35, 42, …
M₈: 8, 16, 24, 32, 40, 48, …
M₉: 9, 18, 27, 36, 45, 54, …

Observăm că numerele 4, 6, 8, 9 etc. apar în diverse şiruri de multipli, pe diferite poziţii. Dimpotrivă, numerele 2, 3, 5, 7 etc. apar în aceste şiruri doar pe prima poziţie; de aia ele se numesc numere prime. Într-adevăr, acestea se numesc numere prime pentru că apar în şirurile de multipli doar pe prima poziţie! Cu această ocazie am aflat deci, de ce se numesc aşa. În alte limbi, cum ar fi germana, nu pot fi făcute astfel de conexiuni; cu atât mai păcat este să ratăm o ocazie ce ne-o oferă “pe tavă” limba noastră.

Această mişcare a fost posibilă pentru că am înlocuit în limbajul folosit noţiunea de multiplu în sens riguros teoretic cu noţiunea de multiplu în sens istoric. Mai putem face un pas în acest proces şi să analizăm cum stau lucrurile dacă apelăm şi la noţiunea de multiplu în sens lingvistic: multiplii unui număr reprezintă numărul luat de mai multe ori (multiplu = de mai multe ori); multiplul unui număr subînţelege că acel număr este la plural, nu la singular, adică nu este luat doar o singură dată. Aceasta este de fapt cea mai naturală formă de a vorbi despre multipli.

De aici apare Ciurul lui Eratostene, o lecţie foarte practică, din păcate de mult abandonată de învăţământul nostru vitezoman, ce nu-şi mai găseşte timp pentru astfel de fleacuri. În Ciurul lui Eratostene exact asta se întâmplă: încercuim primul număr după 1, adică pe 2 (pe 1 de mult l-am exclus din aceste jocuri, deci copiii n-au nici o problemă în a începe de la 2) şi apoi tăiem toţi multiplii lui 2 – toţi multipli în sens lingvistic; acum primul număr rămas netăiat este 3; îl încercuim pe 3 şi tăiem apoi toţi multiplii săi – toţi multiplii în sens lingvistic, şi aşa mai departe cu următoarele numere prime.. Astfel, în Ciurul lui Eratostene apare o altă faţetă a multiplei personalităţi a numerelor prime, anume că numerele prime reprezintă numerele rămase în Ciurul lui Eratostene după ce tăiem toţi multiplii (toţi multiplii în sens lingvistic).

Acest aspect iese foarte bine în evidenţă dacă faceţi Ciurul lui Eratostene până la 250 (ştiu, nu-i uşor). După lunga muncă de rutină de încercuit un număr prim şi tăiat toţi multiplii săi, până la 11 şi multiplii săi, care sunt încă uşor de găsit, la 13 apare întrebarea dacă mai sunt multipli de-ai săi încă netăiaţi. Aici îi confrunt pe elevi cu o întrebare ajutătoare: “care a fost primul număr tăiat la şirul lui 5? Sau la şirul lui 7?”. După o scurtă dezbatere elevii observă că este vorba de pătratul numărului prim la care tocmai lucram. Când l-am încercuit pe 5 ca prim, mulţi din multiplii săi erau deja tăiaţi de la şirul lui 2 sau de la şirul lui 3. Primul care nu era tăiat şi l-am tăiat proaspăt era 25. La fel, primul multiplu tăiat doar la şirul lui 7 a fost 49. O verificare scurtă şi la 11 ne convinge: la şirul multiplilor lui 13 nu mai trebuie să verificăm, primul ce încă n-a fost eliminat este 169. În continuare mai găsim de tăiat doi multipli de-ai lui 13, pe 13 ∙ 17 = 221 şi pe 13 ∙ 19 = 247. Acum trecem la următorul număr prim, la 17. Care este primul multiplu al lui 17 ce încă nu este eliminat din Ciurul lui Eratostene? Clar, este 17² = 289, dar care este deja în afara limitei ce ne-am propus-o. Înseamnă că toate numerele rămase încă netăiate sunt numere prime (observaţie valabilă în lista numerelor până la 250). Acum se înţelege desigur că dacă vrei să faci la clasă Ciurul lui Eratostene cu copiii, fiecare în caietul lui, îţi ocupă din plin o oră.

Câteva precizări metodice merită făcute, legat de această lecţie. Eu m-am străduit să scriu cât mai mic, pentru ca să-mi încapă 25 de rânduri pe înălţimea de 1,10 m a tablei. Elevii trebuiau să înceapă o pagină nouă, pe lângă titlul – care pe tablă era alături – având întreaga pagină la dispoziţie. Oricum, trebuie atenţionaţi să copieze tabelul exact ca pe tablă, pentru a avea o ordine în care să se descurce (unii totuşi tot nu reuşesc). Pentru o ordine cât mai clară, eu îl scriu pe 1 la început, iar apoi îl şterg când începem munca la ciur. Desigur că, după completarea tabelului, luăm o scurtă pauză în care le povestesc ce este acela un ciur pentru sortat pietrişul pe diferite mărimi.

Apoi, aşa cum se vede şi în poza de final a tablei, la primele “site” ale ciurului folosesc la fiecare câte o culoare diferită; de-abia de la 13 nu mai schimb culoarea cretei pentru restul numerelor prime găsite. Ora următoare aruncăm o privire înapoi în care scriem întâi lista numerelor prime cel puţin până la 100 (anul acesta elevii au vrut să mergem mult mai mult), ordonate de data asta pe coloane: prima coloană cele de o cifră, a doua coloană cele între 10 şi 20 (câte patru pe fiecare coloană), apoi cele două dintre 20 şi 30 (două numere prime), pe a patra coloană cele între 30 şi 40, apoi cele între 40 şi 50 (trei numere prime) ş.a.m.d. Apoi facem o analiză cu tot ce-am observat. De pildă că într-o decadă pot fi cel mult patru numere prime (la primele două coloane, dar şi mai târziu, de exemplu între 190 şi 200), dar şi că există decade fără numere prime ( am avut una între 200 şi 210).

Ca o curiozitate le povestesc şi despre numerele prime gemene (numere prime despărţite doar de numărul par dintre ele), despre felul în care acestea sunt scrise, de pildă 2⁶∙3±1 pentru 191 şi 193, dar şi scurt, superficial, despre faptul că numerele prime gemene foarte mari, încă necunoscute pentru restul lumii, sunt folosite la codificarea mesajelor secrete pe internet.

Pasul 3) O nouă sesiune de întâlniri cu numerele prime apare desigur atinci când începem să discutăm despre divizorii unui număr. Aici, în sfârşit, lucrurile ajung “în ape cunoscute” pentru majoritatea părinţilor, care au trebuit să îndure cu stoicism o materie necunoscută lor, materie care nu prea semăna cu definiţia ce o ţineau ei minte din liceu. Aici discutăm despre divizori propri şi divizori impropri şi putem spune în sfârşit că numerele prime sunt acele numere care se divid doar la unu şi la el însuşi, sau, cu alte cuvinte, că numerele prime sunt numerele care au doar divizori impropri. Spre deosebire de acestea, numerele compuse au întotdeauna şi cel puţin încă un divizor propriu în plus. Merită aici să vă prezint o definiţie găsită într-o veche carte germană (G. Ulrich, Arithmetik und Algebra, 1940): numărul prim este un număr care nu este divizibil prin nici un alt număr (în afară de 1). Această descriere elimină foarte abil divizorul numărul însuşi, prin forma exprimării (nu este divizibil prin nici un alt număr).

Artificiul de exprimare îmi aduce aminte de felul cum poţi ridica la pătrat un număr cu un calculator de buzunar. De pildă, pentru 17² trebuie să apăsăm 17 x = şi obţinem instant 289, pentru că gândirea calculatorului înmulţeşte număr iniţal cu numărul de pe ecran, odată ce ai apăsat semnul egal.

Înainte de a încheia acest eseu “filozofic” despre numerele prime, îmi permit două ultime reveniri scurte la subiectul multiplilor unui număr (acestea au fost doar parţial prezentate elevilor). În primul rând, ne aducem aminte că la divizorii unui număr natural avem întotdeauna, sigur cel puţin doi divizori*, anume numărul 1 ca divizor universal, şi numărul însuşi, cele două numere purtând numele de divizori impropri; ceilalţi divizori se numesc divizori propri. În mod analog putem privi lucrurile şi la multiplii unui număr: orice număr îl are pe 0 (zero) ca multiplu universal şi pe numărul însuşi ca multiplu, cei doi multipli putând fi denumiţi în mod similar multipli impropri. Ceilalţi multipli, pe care i-am caracterizat mai devreme ca “plurali”, vor putea fi numiţi în mod similar drept multipli propri. Astfel (după ce am eliminat cei “doi ciudaţi”, 0 şi 1) numerele prime sunt numerele rămase după excluderea tuturor multiplilor propri din lista numerelor naturale. (* în afara cazului numărului 1, care are doar un divizor; aici găsim încă o explicaţie pentru care numărul 1 nu este considerat prim: numerele prime sunt acele numere care au exact doi divizori)

A doua revenire legată de multiplii se referă la expresia folosită de multiplu în sens lingvistic (fără zero şi numărul însuşi, adică multiplu drept un “plural”) spre deosebire de multiplu în sens riguros teoretic (varianta folosită actualmente şi şcoli) sau varianta intermediară de multiplu în sens istoric (doar fără zero, care nu era cunoscut în antichitate). Am discutat cu un expert lingvist, care mi-a sugerat termenul de multiplu în sensul uzanţei generale, folosit de toată lumea, pentru multiplul plural (adică fără 0 şi 1), respectiv multiplu în sens restrâns, folosit doar de către matematicieni (pentru toţi multiplii în sens ştiinţific). Acest punct de vedere se aseamănă cu situaţia greutăţii (termen folosit în sens larg de către toată lumea), respectiv a masei (termenul ştiinţific corect pentru mărimea măsurată în kg, dar folosit în cerc restrâns, doar în lumea ştiinţifică a fizicii şi a domenilor conexe).

28 Dec. 2016

Titus Grigorovici

Pe cât sunt considerate de cunoscute, pe atât sunt totuşi percepute ca profund enigmatice. Dar, orice-ar fi, când le aud pronunţat numele, în sufletul lor oamenii “iau poziţie de drepţi”, atenţia fiecăruia se acutizează, încearcă eventual să-şi aducă aminte definiţia învăţată în şcoală şi o mică spaimă se face simţită în sufletul unora: “dacă voi fi întrebat ceva despre ele, ceva ce nu ştiu?”. Numerele prime, prin simpla lor prezenţă, sunt nişte entităţi matematice ce impun respect. Cu atât mai mult, nu ne aşteptăm ca numerele prime să apară în preocupările unor persoane autiste.

Pentru noi, profesori la şcolile obişnuite se întâmplă mai rar, dar uneor totuşi se întâmplă, să avem în clasă câte un elev autist. O colegă a avut pe vremuri un elev autist în şcoala unde predam; nu l-am cunoscut direct decât la o supraveghere pentru simularea examenului de Capacitate. Acest elev desena foarte frumos, desene pline de detalii. La acea simulare, în loc de rezolvări la matematică, acesta a desenat o foarte frumoasă vază cu flori, plină de detalii filigranate. Am păstrat acel desen în amintirea elevului respectiv. A fost cea mai specială lucrare primită vreodată de la un elev.

Uneori elevii autişti pot reprezenta pentru profesorul norocos o fereastră deosebită spre “gândirea matematică”. Am scris gândirea matematică cu ghilimele pentru că în aceste cazuri este vorba despre o gândire ieşită din tiparele obişnuite. Iar această situaţie ne poate învăţa să respectăm şi alte modele de gândire, decât cele pe care le întâlnim şi le predăm în activitatea de zi cu zi.

Atunci când au abilităţi matematice neobişnuite, aceste persoane uimesc pe cei din jur cu înclinaţii într-o direcţie îngustă a matematicii, pe care însă o pot pătrunde în profunzimi de neimaginat pentru omul de rând. Un astfel de caz, cu o memorie uriaşă şi o abilitate incredibilă de numărare, este evocat în filmul Rain Man din 1988, în care Dustin Hoffman, joacă rolul unui personaj autist. La un moment dat acesta “vede” aproape dintr-o privire 246 de scobitori vărsate pe jos de o chelnăriţă, care tocmai încercase să deschidă o cutiuţă nouă, sigilată din fabrică . Fratele său, jucat de Tom Cruise, întreabă: “Câte erau în cutie?”, iar chelneriţa, citind de pe ambalaj, îi răspunde “250”. “Destul de aproape!” se miră acesta, dar chelneriţa îi replică “mai sunt patru în cutie”. Puteţi găsi scena pe YouTube dând spre căutare Rain Man 246.

Povestea ce urmează este preluată din lucrarea lui Oliver Sacks – Omul care îşi confunda soţia cu o pălărie, apărută în 2011 la Editura Humanitas. Autorul este medic şi profesor de neurologie şi psihiatrie la Centrul medical al Universităţii Columbia, iar lucrarea prezintă diferite cazuri din experienţa sa îndelungată. Povestea cu numărul 23 din această carte are titlul simplu Gemenii şi este cuprinsă între paginile 229-251. Iată în continuare spicuiri din acest articol.

Când i-am întâlnit pentru prima oară pe gemenii John şi Michael, în anul 1966, într-un spital de stat, ei erau deja bine cunoscuţi. Apăruseră la radio şi la televiziune şi făcuseră obiectul unor relatări amănunţite, ştiinţifice şi populare. … îşi croiseră drum în literatura ştiinţifico-fantastică, uşor “literaturizaţi”…

Gemenii, care aveau vârsta de douăzeci şi şase de ani, trăiseră în instituţii specializate, fiind diagnosticaţi ca autişti,…. Cele mai multe relatări …erau legate de … folosirea unui algoritm calendaristic inconştient prin care puteau să spună imediat în ce zi a săptămânii cădea o dată din trecutul sau din viitorul îndepărtat. …

Nu se poate obţine într-adevăr nici un indiciu despre ce se află în profunzime decât dacă lăsăm deoparte testele asupra gemenilor … e nevoie să ne apropiem de gemeni, să-i observăm cu înţelegere şi calm, fără prejudecăţi, cu deschidere fenomenologică şi tact, urmărindu-i cum trăiesc, gândesc şi interacţionează în linişte, ducându-şi spontan vieţile lor neobişnuite….

Sunt mici de statură, … cu o miopie degenerativă avansată, necesitând ochelari cu lentile atât de groase încât ochii lor par deformaţi, ca ai unor profesori caricatural de mici …. Iar această impresie e întărită imediat ce li se pune vreo întrebare sau li se oferă prilejul să înceapă în mod spontan “numărul” obişnuit, ca nişte marionete. …(la diferite spectacole sau la televiziune)

În aceste condiţii, prestaţiile lor au devenit monotone. Gemenii zic: “Spuneţi o dată, oricare din ultimii sau din următorii patruzeci de mii de ani.” Li se dă o dată şi, aproape imediat, ei spun în ce zi a săptămânii cade. “Încă o dată!” strigă ei, şi jocul se repetă. Pot spune şi ziua în care cade Paştele în acest interval de 80 000 de ani. …

…Dacă sunt întrebaţi cum pot reţine atât de multe în minţile lor – un număr format de trei sute de cifre … – ei răspund simplu: “Le vedem.” … Prima mea observaţie legată de aptitudinile “naturale” şi de metoda “naturală” a gemenilor s-a născut într-un mod …spontan … mai curând comic.

De pe masa lor a căzut o cutie de chibrituri care şi-a vărsat conţinutul pe jos: “111” au strigat amândoi simultan; apoi, în şoaptă, John a zis: “37”. Michael a repetat numărul, John l-a mai spus o dată şi s-a oprit. Am numărat chibriturile – mi-a luat ceva timp – şi erau 111. “Cum aţi putut număra chibriturile aşa repede?” am întrebat. “N-am numărat”, au zis ei. “Am văzut că erau 111.”…

“Dar de ce aţi şoptit 37 şi aţi repetat acest număr de trei ori?” i-am întrebat pe gemeni. Au răspuns într-un glas: “37, 37, 37, 111.”

Acest lucru m-a uimit şi mai tare …Că vedeau 111 – “o-sută-unsprăzecitatea” – instantaneu era ceva ieşit din comun, …Dar ei ajunseseră la “divizorii” numărului 111 fără să aibă vreo metodă, fără măcar să “ştie” (pe cale obişnuită) ce înseamnă divizorii. …acum, în mod spontan, împărţiseră un număr divizibil în trei părţi egale.

Întrerup şirul citatelor din Oliver Sacks cu observaţia că în ultima frază un număr divizibil ar trebui citit cu sens de  un număr decompozabil, un număr care se poate descompune ca produs de alte două numere (diferite de 1, desigur). Dar poate fraza se citeşte şi mai corect astfel: ei împărţiseră aditiv, în trei părţi egale un număr ce era divizibil în trei părţi egale (citiţi divizibil nu cu sens matematic – împărţibil exact, ci în sens latin – despărţibil; probabil că acesta este şi sensul original al cuvântului din matematică).

“Cum aţi calculat?” am întrebat cam repezit. Mi-au explicat, atăt cât puteau ei de bine, în termeni sărăcăcioşi, insuficienţi … că nu “calculaseră”, ci “văzuseră” într-o străfulgerare. John a făcut un gest cu degetul mare şi alte două degete întinse, care părea să sugereze că tăiaseră spontan numărul în trei părţi egale, printr-un fel de “fisiune” numerică spontană. Păreau uimiţi de uimirea mea, de parcă eu aş fi fost într-un anume sens orb; …

M-am gândit la această problemă, dar fără mult succes. Apoi am uitat de ea. Am uitat până când s-a petrecut, cu totul întâmplător, a doua scenă spontană, o scenă magică.

De data asta erau aşesaţi împreună într-un colţ, zâmbind secretos, misterios, un zâmbet pe care nu-l mai văzusem până atunci, trăind o plăcere stranie şi o stare de pace. M-am furişat pe nesimţite, ca să nu-i deranjez. Păreau prinşi într-un dialog neobişnuit, pur numeric. John spunea un număr – un număr de şase cifre. Michael recepţiona numărul, încuvinţa din cap, zâmbea şi părea că-l savurează. Apoi, la rândul lui, spunea un alt număr de şase cifre, iar acum John era cel care-l recepţiona şi se bucura din plin de el. La prima vedere, semănau cu doi degustători de vinuri, împărtăşind bucheturi rare, aprecieri rare. Am rămas nemişcat, nevăzut de ei, hipnotizat, uluit.

Ce anume făceau? Ce naiba se petrecea? Nu pricepeam nimic. Era poate un fel de joc, dar avea o gravitate şi o intensitate, un fel de intensitate senină, meditativă şi aproape sacră, pe care n-o mai văzusem niciodată într-un joc obişnuit, şi pe care n-o mai observasem la aceşti gemeni, de regulă agitaţi şi zăpăciţi. M-am mulţumit să notez numerele pe care le rosteau – numere care de bună seamă le procurau atâta plăcere, şi pe care le “contemplau”, le savurau şi le împărtăşeau.

Aveau oare numerele vreo semnificaţie, mă întrebam în drum spre casă, aveau ele vreo semnificaţie “reală” ori universală, sau doar o semnificaţie excentrică, personală, ca secretele şi “limbajul” stupid pe care-l inventează uneori fraţii şi surorile pentru ei înşişi? … John şi Michael nici măcar nu foloseau cuvinte sau jumătăţi de cuvinte – pur şi simplu îşi pasau numere de la unul la altul. …

Ajuns acasă, am scos tabele cu puteri, divizori, logaritmi şi numere prime – amintiri şi relicve dintr-o perioadă stranie a copilăriei mele, când “vedeam” şi eu numere, eram pasionat de ele. Aveam deja o presimţire, iar acum se confirma. Toate numerele, numerele de şase cifre, pe care le schimbaseră gemenii între ei, erau numere prime – adică numere care nu erau divizibile cu alte numere întregi decât cu ele însele sau cu unu. Văzuseră sau avuseseră ei oare o carte ca a mea, ori erau în stare să “vadă” numere prime, pe o cale de neînchipuit, cam în acelaşi fel în care văzuseră “o-sută-unsprăzecitatea”? …

În ziua următoare m-am întors la spital luând cu mine preţioasa carte cu numere prime. I-am găsit din nou închişi în comunitatea lor numerică, dar de data aceasta m-am alăturat şi eu, în tăcere. La început au fost surprinşi, dar, văzând că nu-i întrerup, şi-au reluat “jocul” cu numere prime din şase cifre. După câteva minute, m-am hotărât să intru în joc şi am lansat un număr de opt cifre. S-au întors amândoi spre mine, au tăcut brusc, uimiţi, părând că se concentrează intens. A urmat o pauză lungă – cea mai lungă pe care o observasem până atunci la ei, trebuie să fi durat o jumătate de minut sau mai mult – apoi, dintr-o dată, simultan, au început amândoi să zâmbească.

Văzuseră brusc, după un proces intern de verificare imposibil de închipuit, că numărul meu de opt cifre era număr prim, iar asta era de bună seamă pentru ei o mare bucurie: în primul rând, pentru că adusesem o nouă jucărie minunată, un număr prim de un ordin pe care nu-l mai întâlniseră până atunci; în al doilea rând, pentru că era limpede că eu înţelesesem ce făceau, îmi plăcea, îi admiram şi puteam intra şi eu în joc.

S-au dat uşor în lături, făcându-mi loc şi mie, un nou tovarăş de joacă, al treilea în lumea lor. Apoi John, care prelua mereu iniţiativa, s-a gândit un timp foarte îndelungat – trebuie să fi fost cel puţin cinci minute, deşi nu îndrăzneam să fac nici o mişcare şi abia respiram – şi a scos la iveală un număr de nouă cifre; iar după un timp comparabil, gemenul său Michael a răspuns cu unul similar. Apoi eu, după ce mă uitasem pe furiş în cartea mea, mi-am adus, trişând, propria contribuţie: un număr prim de zece cifre pe care îl găsisem în carte.

S-a lăsat din nou, pentru şi mai mult timp, o linişte uimită; apoi John, după o contemplare lăuntrică formidabilă, a scos la iveală un număr de douăsprezece cifre. Nu aveam cum să-l verific şi nu puteam să-i răspund: în cartea mea … nu erau numere prime cu mai mult de zece cifre. Dar Michael era la înălţime, deşi îi trebuiseră cinci minute, iar peste o oră gemenii schimbau între ei numere prime de douăzeci de cifre, cel puţin aşa cred, întrucât nu aveam nici un mijloc de verificare. De altfel, în 1966 nici nu era un lucru simplu dacă nu aveai la dispoziţie un calculator sofisticat. Chiar şi aşa ar fi fost greu, fiindcă, fie că foloseşti ciurul lui Eratostene, fie că foloseşti orice alt algoritm, nu există o metodă simplă pentru calculul numerelor prime. Nu există nici o metodă simplă pentru determinarea numerelor prime de acest ordin – şi totuşi gemenii o făceau.

Articolul se încheie cu diverse analize filozofice ale cazului, dintre care spicuiesc doar câteva rânduri: …numerele nu sunt pentru ei doar un obiect de cult, ci şi prieteni – poate singurii prieteni pe care i-au cunoscut în vieţile lor izolate, autiste. E un sentiment destul de răspândit printre cei înzestraţi pentru numere …

Matematicianul Wim Klein a exprimat foarte clar acest lucru: “Numerele sunt oarcum prietenii mei. 3844 nu înseamnă acelaşi lucru pentru tine, nu-i aşa? Pentru tine este doar un trei, un opt, un patru şi un patru. Dar eu spun: Salut , 62 ridicat la pătrat!”

Cred că gemenii, aparent atât de izolaţi, trăiesc într-o lume plină de prieteni, au milioane, miliarde de numere cărora le spun “Salut!” şi care, sunt sigur, le răspund la salut. Dar nici unul dintre numere nu e arbitrar …, nu se ajunge la el prin vreuna din metodele obişnuite, de fapt nu se ajunge prin nici o metodă, după câte îmi dau seama. La fel ca îngerii, par să aibă acces la o cunoaştere directă. Ei văd direct un univers şi un paradis de numere.

Primul dintre gemeni

În căutarea de exemple cât mai accesibile, dar ne-banale, pentru înţelegerea noţiunii de probabilitate, am găsit acest exemplu deosebit. Da, aţi văzut bine, este un dodecaedru ce are imprimat pe fiecare faţă câte una din cele 12 luni ale unui calendar. Exerciţiile simple de probabilităţi devin brusc mult mai distractive în cazul aruncării unui calendar-dodecaedru: care este probabilitatea să obţinem o lună care începe cu litera i; dar una care începe cu litera m; dar cu a? Putem pune şi întrebarea despre o lună care începe cu o vocală, dar foarte interesantă este şi întrebarea despre probabilitatea de a obţine o lună cu numele de la un număr (de exemplu, septembrie de la şapte etc. Apropo, v-aţi întrebat de ce a 12-a lună are numele decembrie, de la 10; Hmm?).

Dacă nu vă pricepeţi să vă faceţi singuri unul, puteţi descărca un calendar-dodecaedru de pe internet (daţi spre căutare de pildă dodecaedro calendar, iar apoi treceţi pe imagini); găsiţi direct unul din 2017 la adresa http://www.ss42.com/pt/calendar/dodecahedron.html de unde vă recomand să descărcaţi varianta pentru lipire. Atenţie: decupatul şi asmblarea unui astfel de corp durează către o oră, iar calitatea corpului obţinut depinde foarte mult de lipiciul ales (UHU universal s-a dovedit cel mai bun, de găsit în magazinele Kaufland), dar şi de grosimea hârtiei. Sfatul meu este să-l imprimaţi pe o hârtie mai groasă (măcar 90g/mp, pentru a nu avea un dodecaedru prea fragil).

Dodecaedru în (calen)dar

Probabil cea mai cunoscută latură a matematicii zarurilor o reprezintă chiar aspectul său probabilistic. Astfel, alături de banala monedă cu al său 50% (ce frumos sună: fifty-fifty), zarul oferă primele exemple de calcul de probabilităţi cu conexiune în lumea din afara şcolii. Astfel zarul reprezintă echilibrul perfect între banalitatea monedei şi ciudăţenia numită urnă cu bile (câţi elevi au văzut clar o urnă cu bile?; noroc că mai există extrageri Loto la televizor şi le putem explica pe baza acestora urna la care ne gândim noi, profiesorii de mate).

Pe lângă exemplele cu cerinţă număr par sau impar, putem cere elevilor să stabilească probabilitatea ca aruncând un zar să obţinem un număr prim (tot ½  = 50%), sau un divizor al lui 6 (mai interesant, 2/3), sau un număr compus (ce bună reactualizare a noţiunii, pănă îl aflăm pe 1/3).

Dar, orice-am face cu un zar, posibilităţile sarcinilor sunt totuşi limitate. Dacă luăm însă două zaruri, exerciţiile se diversifică simţitor. Dacă mergem de exemplu cu două zaruri de aceeaşi culoare şi îi întrebăm Care este mai mare probabilitatea, de a arunca 2-5 sau 3-3?, s-ar putea ca pe unii dintre elevi să-i derutăm, “să-i băgăm în ceaţă” (şi la unii adulţi vom obţine acest efect). Lecţia se potriveşte perfect a fi abordată prin metoda problematizării. În momentul de dispută maximă vom scoate din celălalt buzunar alte două zaruri, de data asta de culori diferite, şi le voi înlocui pe cele iniţiale. După găsirea răspunsului, putem trece chiar la o fază finală, de lămurire, prin realizarea unui tabel pătrat de 6×6, în care fiecare variantă este prezentată ca pereche ordonată de tipul (2;5), prima cifră fiind scrisă pe tablă întotdeauna cu culoarea primului zar, iar a doua cifră cu culoarea celui de-al doilea zar. În urma realizării acestui tabel, consider că majoritatea elevilor vor fi înţeles fenomenul. Chiar şi conexiuni cu numerele pătrate perfecte şi cu noţiunea de arie sunt posibile în acest moment. (La elevii de peste 14 ani doritori de senzaţii tari, putem întreba despre ce se întâmplă în cazul situaţiei cu trei zaruri.)

Apropo de strădania de a preda şi această lecţie cât mai accesibil: în prima parte a lecţiei de introducere a probabilităţii ca fenomen, în întrebările de început, folosesc deseori cuvântul şansă, ca sinonim pentru probabilitate.

Desigur, dacă avem zaruri cu 12 sau cu 20 feţe, putem relua întrebările despre probabilitate de la zarul tradiţional, extinzându-le la zarul pe dodecaedrul sau la cel pe icosaedru.

6-6, poartă-n casă!

Dacă tot am deschis tolba cu zaruri ciudate, ce ziceţi de nişte zaruri care nici măcar nu mai sunt cubice? Da, există şi aşa ceva, iar cei mai buni candidaţi la astfel de zaruri sunt desigur corpurile perfecte cu mai multe feţe decât şase, aşa-numitele corpuri platonice. Să le luăm la rând: în prima imagine vedeţi un octaedru regulat – cel negru – cu feţe de la 1 la 8, dar şi un decaedru semiregulat – cel muştăriu – cu feţele numerotate de la 0 la 9.

Următoarea imagine prezintă zaruri dodecaedre, cu 12 feţe pentagoane regulate numerotate de la 1 la 12. Cel din stânga este un astfel de zar simplu, pe când cel din dreapta este un dublu dodecaedru cu unul mic în interiorul celui mare. Acestea sunt foarte bune la elevii mici: arunci o dată, iar ei trebuie să facă în minte operaţia cerută cu cele două numere.

Desigur că se pot realiza şi zaruri pe icosaedre, corpuri regulate cu 20 feţe triunghiuri echilaterale. Putem arunca cu două zaruri, sau putem alege icosaedrul dublu; oricum, sarcina de a face în cap adunarea celor două numere este ceva mai dificilă. La fel şi când se doreşte exersarea scăderii sau a înmulţirii. Colegele noastre învăţătoare folosesc mult aceste zaruri în perioada de stabilizare a învăţării operaţiilor. Zarurile icosaedre pot fi folosite la încălzirea minţii şi la clasa a V-a; nu-i uşor să înmulţeşti în cap 17 cu 8, sau 12 cu 15 etc.

Este de la sine înţeles că vom căuta şi la acestea ceva similar cu proprietatea de 7 de la zarurile normale. Elevii deştepţi o intuiesc imediat atunci când le pun un astfel de zar în faţă pe masă şi îi întreb ce număr este dedesupt?. Imediat le luceşte privirea şi îşi adaptează vechile cunoştinţe la noua situaţie. Da, elevii găsesc imediat regula de 13 la dodecaedru, respectiv faptul că la icosaedru suma a două feţe opuse este întotdeauna 21.

Din păcate, astfel de zaruri nu se găsesc în magazinele noastre. Nici în străinatate nu pot fi achiziţionate de oriunde. Zarurile noastre sunt cumpărate din magazinele unor muzee din Germania (Muzeul jucăriilor din Nürenberg, respectiv Deutsches Museum din München). În Cluj am găsit totuşi următoarele două zaruri icosaedre. Acestea nu au însă feţele numerotate respectând regula ca suma feţelor opuse să fie constantă. La acestea feţele sunt numerotate pentru a putea ţine un scor la un joc; astfel de la orice număr se poate trece la numărul următor pe faţa vecină printr-o simplă răsturnare a zarului. Ultima dată am întâlnit un zar pe dodecaedru în vară,la un joc oferit de reţeaua de magazine Lidl, dar acesta avea fiecare număr de la 1 la 6 de câte două ori, folosind doar facptul că dodecaedrul se rostogoleşte foarte uşor şi are o asemănare interesantă cu mingea de fotbal.

Tolba cu zaruri

Când vorbim despre zaruri, ne gândim desigur că vom găsi pe feţele sale numerele de la 1 la 6, reprezentate cu punctuleţe, într-o formă inteligibilă oricărei epoci de cultură. Ce gândiţi însă dacă vedeţi un zar cum sunt cele din imaginea următoare?

Da, aţi văzut bine, aceste zaruri au pe feţele lor puterile lui 2, adică 2⁰ = 1, 2¹ = 1, … 2⁶ = 64. La ce ne pot ajuta astfel de zaruri? Păi, de pildă la clasele gimnaziale le putem cere elevilor să zică instant puterea lui 2 corespunzătoare feţei de sus. O sarcină mai interesantă ar fi să le cerem elevilor să verifice cum se aplică la aceste zaruri proprietatea de 7 găsită la zarurile obişnuite. Păi, produsul a două feţe opuse trebuie să fie întotdeauna egal cu 2⁷ = 128. Logic, nu!

Profu’ cu zaru’

În postarea precedentă am vorbit despre proprietatea de 7 a zarului, anume că la orice zar (corect construit) suma feţelor opuse este întotdeauna 7 (feţele opuse 1 + 6; 2 + 5 respectiv 3 + 4). Această proprietate, prezentă încă de la începuturile antice ale zarului, o folosesc în diverse situaţii, cum ar fi în cazul primei lecţii despre cub. Pentru postarea de faţă doresc să vă prezint aplicaţii ale acesteia în două probleme de matematică distractivă.

Prima este preluată din Martin Gardner, Mathematics, Magic and Mystery, Ed.Dover Pub. 1956 (eu am un exemplar în limba germană, Matematische Zaubereien, Ed. DuMont, 2004, pag. 61). Este vorba de fapt de o scamatorie matematică cu trei zaruri, pe care o descriu în continuare.

Îi dau unui elev voluntar din clasă cele trei zaruri, rugându-l să urmeze întocmai instrucţiunile mele, în timp ce eu voi sta cu spatele către masa unde el execută cerinţele (ceilalţi elevi pot sta în jur pentru a vedea „spectacolul”). Odată întors îi cer elevului să efectueze o aruncare cu cele trei zaruri şi să adune cele trei numere obţinute (valorile de pe feţele de deasupra). Într-un al doilea pas îl rog pe elev să întoarcă la alegere unul din zaruri, astfel încât faţa de jos să ajungă deasupra, iar apoi să adune şi acest nou număr la suma iniţială (celelalte două zaruri rămân aşa cum au căzut la început). În al treilea pas elevul trebuie să ia zarul pe care l-a întors deja şi să-l mai arunce numai pe acesta încă o dată, iar numărul obţinut să-l adune la suma existentă pănă atunci. În tot timpul cât stau cu spatele elevul nu îmi spune nici unul din numerele cu care lucrează, şi nici suma finală.

Chiar şi aşa, în acest moment eu mă întorc şi fără să ştiu care din cele trei zaruri a fost cel întors de mai multe ori, spun totuşi suma finală calculată de elev în minte. Cum fac? Simplu: adun 7 la suma care o văd în acel moment pe masă. Problemuţa se iveşte de la sine: cum face profu’?, şi este foarte frumoasă pentru că oferă destul de repede o primă aplicaţie uşoară a folosirii literelor în calcul. Astfel, după încă una-două „reprezentaţii”, putem să ne gândim să demonstrăm scamatoria. Iată o variantă posibilă: notez cu x, y, z cele trei numere iniţiale, şi presupunem că elevul s-a hotărât să întoarcă zarul cu numărul y. Atunci suma totală va fi:

x ₊ y + z + y_opus + y’ = x + z + y’ + 7

Am notat cu y_opus faţa opusă lui y, iar cu y’ numărul obţinut pe zarul ţinut pe zarul y la a doua aruncare. Ca tehnică de inducere în eroare – magicienii aşa fac – până fac suma x + z + y’ şi apoi adun 7, pot să atrag atenţia auditoriului că eu nu am de unde să ştiu care din cele trei zaruri a fost întors de două ori şi care sunt cele două zaruri care au rămas pe loc după prima aruncare.

A doua scamatorie, tot cu trei zaruri, este de fapt o variaţiune a problemei cu zece zaruri din postarea precedentă şi este preluată din Michael Holt, Math Puzzles and Games, Ed. Walker Pub. 1977 (eu am preluat-o din varianta în limba germană, Neue mathematische Rätsel, Ed. DuMont, 2005, pag. 83).

Daţi zarurile „elevului voluntar” cu recomandarea ca, în timp ce dvs. staţi cu spatele întors, el să aranjeze cum doreşte un turnuleţ din cele trei zaruri. În timp ce le aranjează, trebuie doar să adune toate feţele care nu se vor putea vedea în final din nici o parte (numerele de pe acestea). După ce a terminat, şi aceste feţe nu se mai pot vedea, dvs. vă întoarceţi şi puteţi foarte repede să-i spuneţi ce sumă a obţinut. Cum procedaţi? Pur şi simplu observaţi numărul arătat de zarul din vârf şi îl scădeţi din 21.

Titus Grigorovici

De obicei, când ne gândim la acest subiect, ca profesori de matematică, ne vin în minte în primul rând probabilităţile. Acest aspect este subliniat foarte bine în limba germană, unde zarul se numeşte Würfel (se poate traduce ca “aruncăreaţă”); încă ceva interesant, anume nemţii folosesc acelaşi cuvânt şi pentru cub. Apropos, ştiaţi de unde provine cuvântul zar? Din arabă, unde cuvântul se pronunţă la fel: zhar (complet: Al-zhar). Evident că de aici vine şi cuvântul hazard (cu trimitere la probabilitate), dar pentru seria pornită cu această ocazie doresc să tratăm şi alte aspecte ale zarului, decât doar cele legate “abilităţile zarului de a oferii numere la întâmplare”.

Zarurile sunt cunoscute în forma actuală din Antichitate. De pildă, în ruinele oraşului minier Berenice Pancrisia din Egiptul antic s-a găsit un zar de bronz având exact structura celor de azi (din Enzo Bernardini, Atlas de arheologie – Marile descoperiri ale civilizaţiilor antichităţii, Ed.Aquila, 2006, pag. 63), numerele de pe feţe fiind reprezentate cu punctuleţe (mici găurele), exact aşa cum le ştim actualmente.

Proprietatea de bază a aranjării numerelor pe feţele zarului este, pe cât de surprinzătoare, pe atât de logică: la orice zar construit corect suma feţelor opuse este întotdeauna 7. Simplu, clar, deşi puţină lume are cunoştinţă de această proprietate.

Elevilor le-o putem oferii ca atare, sec, sau putem face din apariţia ei o mare bucurie. De pildă, eu o folosesc pentru a înlătura “spaima” din ochii copiilor de clasa a IV-a, ţinând o lectie distractivă, atunci când merg prima dată în vizită la ei ca să ne cunoaştem. Astfel, iau un zar şi merg pe rând pe la toţi elevii, ţinând zarul între două degete, aşezat pe masă, cu întrebarea: ce număr este pe faţa de jos? Ei ghicesc, iar apoi eu ridic zarul infirmând, mai rar confirmând, răspunsul. Desigur că zarul este învârtit în mod spectaculos, chiar ostentativ, la trecerea de la un elev la următorul. După câţiva elevi mă opresc şi mă adresez clasei frontal: oare ce şmecherie o fi aici? Apoi, mai continui de la un elev la celălalt. Şi iarăşi acţionez frontal. Totul până când un elev are o idee ajutătoare. Dacă apare o idee bună, ajut şi eu în elucidarea enigmei, dar ideea iniţială trebuie să vină de la elev. Eventual, scot din pungă mai multe zaruri adunate de-a lungul timpului (multe zaruri frumos colorate le am din magazine second-hand, achiziţionate la preţuri derizorii), şi le dau câte un zar la fiecare bancă să le analizeze. Ultima dată am găsit regula până la parcurgerea a jumătate de clasă. Apoi, în starea de bucurie a descoperirii acestei reguli noi, am mai făcut exersări cu alţi elevi pentru a stârnii satisfacţia elevilor.

Pasul următor de gândire l-am făcut apoi cu o problemă la care am verificat capacitatea de a aplica cunoştinţele nou învăţate: Construim un turn din zece zaruri, despre care ştim că numărul arătat de ultima faţă de sus este trei. Căt este suma tuturor feţelor orizontale ale celor zece zaruri, care nu pot fi văzute (chiar dacă ne-am învârti în jurul turnului)? (Aceasta este o problemă foarte veche, din categoria matematică distractivă; se pare că cea mai recentă apariţie a acesteia este în lucrarea lui Armand Martinov, Matematica…o plăcere, Ed. Sigma, 2003, pag.18)

Ultima oară chiar am construit un astfel de turn din zece zaruri, dar nu i-am lăsat pe elevi să vină să se învârtă în jurul acestuia, pur şi simplu pentru a nu-l dărâma în înghesuiala posibilă. De fapt, cu această problemă dată ca temă am şi încheiat ora. Este greu de descris bucuria elevilor a doua zi de dimineaţă, când veneau la mine să mă anunţe cum au rezolvat ei problema. Desigur că nu au scăpat aşa de uşor: la următoarea oră, cei care au avut răspuns corect au trebuit să explice clar în faţa colegilor cum au gândit (aici ies la iveală şi cazurile când n-au gândit elevii, ci părinţii).

Titus Grigorovici