Găsirea numărului π este un proces ce poate fi prezentat elevilor pe toate nivelurile de complexitate, iar arta predării înseamnă a găsi acele căi de parcurs la clasă care să le fie accesibile elevilor şi să-i stârnească în procesul gândirii, căi din care să înţeleagă fenomenul şi pe baza cărora să poată apoi lucra independent sarcinile primite ca temă.
Pare simplu şi totuşi de multe ori o dăm în bară. Eu, de pildă, am dat-o “pe de lângă” destul de urâţel în noiembrie 2019 chiar cu ocazia unei lecţii deschise la care – culmea – eu m-am înscris să o ţin. Pe scurt, am dorit să introduc acest număr, dar am făcut greşeala de a încărca lecţia mult prea tare cu diferite elemente, astfel încât lecţia pregătită şi clasa respectivă au avut foarte puţine momente în comun. Pentru ce am greşit eu mi-am luat timp şi am încercat să analizez cât mai obiectiv, după principiul “greşelile sunt bune dacă înveţi din ele”. Seria începută acum reprezintă de fapt gestul de corectură pentru respectiva oră deschisă.
Oricum, cu clasa a 7-a am petrecut şi următoarele două ore din program cu lămurirea subiectului respectiv. Elevii, în general cei buni desigur, aveau foarte multe întrebări, multe nelămurite de către cei de acasă. Pe lângă aceştia mai era şi o parte foarte consistentă a clasei care avea aerul “de parcă trecuse trenul peste ei”. Apropos, aici am atins un aspect de care noi profesorii de matematică nu prea suntem conştienţi: cei mai mulţi elevi nu înţeleg o lecţie “din prima”, aşa încât ar fi nevoie de un sistem de lecţii în care să reluăm cunoştinţele predate câteva ore, desigur tot în altă formă (până “le intră în cap”). Noi, profesorii, greşim aici pentru că avem impresia că “dacă le-am predat o chestie, ei şi trebuie să o ştie”. Nu-i deloc aşa; o vor şti eventual vârfurile clasei, cât şi cei care au acasă pe cineva care să e explice imediat ce s-a întâmplat. Mai există şi cei puţini care au forţa de a se duce acasă şi a se lupta cu noua situaţie până o înţeleg. Cei mai mulţi însă se prind despre ce-i vorba doar în următoarele ore (în cazul în care aceste ore reiau subiectul). În cazul de faţă, apariţia acestui număr ciudat, notat cu o literă necunoscută (de unde-i?, grecească? de ce? ce vrea să însemne ăsta?), această apariţie oricum îi bulversează puternic pe majoritatea (acelaşi fenomen l-am observat la apariţia ciudatei acolade de la sistemele de ecuaţii). În general, orice nouă apariţie care nu seamănă cu cele deja cunoscute, se pare că îi sperie pe foarte mulţi. În primul rând, aceste situaţii ar trebui contabilizate şi conştientizate de către profesorime, iar în cazul acestora ar trebui acţionat cu mare precauţie la introducerea respectivei noţiuni, pentru a ne asigura că ducem cu noi “în plutonul celor care au înţeles” cât mai mulţi elevi ai clasei (mă refer aici măcar la cei din corpul central al clasicului “clopot al lui Gauss”).
Stimaţi colegi, noi nu am fost formaţi să avem grijă la astfel de aspecte de ordin psihologic, dar se pare că elevii actuali sunt foarte sensibili în acest sens. Ca o scurtă paranteză, trebuie să precizez că respectiva clasă o luase oricum cam puternic pe o pantă descendentă în ceea ce priveşte învăţatul, fenomenul accentuându-se în săptămânile următoare. Astfel, am fost nevoit să iau măsuri mai hotărâte (blânde desigur, dar hotărâte) astfel încât situaţia să se redreseze pe o pantă pozitivă.
Revenind la introducerea cunoştinţelor despre măsurarea cercului şi la studiul numărului π, părerea mea actuală este că această lecţie ar trebui să se desfăşoare pe parcursul mai multor ore, într-un proces având punctul de pornire la un nivel cât mai simplu (nivel la care să se conecteze tot colectivul) şi care să urce treptat pănă la nivelul maxim al elevilor cei mai buni din clasă (deci nu doar la acest nivel, aşa cum procedează mulţi colegi cu pretenţii de excelenţă), parcursul desfăşurându-se pe două căi importante în paralel: exemple din procesul istoric de găsire a numărului π, pe de-o parte, cât şi exemple aplicative de calcul a lungimii şi a ariei cercului. Lecţia ar trebui să se desfăşoare într-o formă care să respecte cât mai mult atât aspectele psihologice (tot mai mulţi elevi trăiesc într-o “supă psihologică” greu de imaginat pentru noi matematicienii), cât şi aspectele istorice de descoperire a elementelor de măsurare a cercului (aspecte deseori profund diferite de formele de predare de sorginte academică, dragi sufletului de profesor format în ultimii 30-40 de ani).
Prin actuala serie de postări mi-am propus să prezint orientativ forma la care am ajuns pe parcursul ultimilor ani, desigur şi pe baza experienţei (ceva cam greu de digerat) din toamnă, de la actuala clasă a 7-a. Materialul ce urmează reprezintă rodul un proces de acumulare de lungă durată şi din multe surse (multe pe care din păcate nu le-am notat la vremea respectivă ca posibilă sursă bibliografică), dar şi cu mult adaos personal, fie pe bază de gândire anticipativă, fie pe bază de experinţă cumulativă.
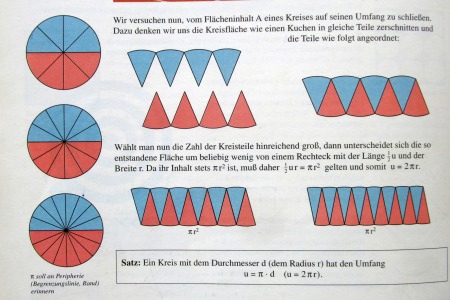
Un ultim argument în favoarea acestei forme îl reprezintă un manual pentru clasa a 10-a (!) din Germania (bănuiesc că acest manual prezintă oricum matereia în a nuştiu-câta reluare). Este un manual pentru Gimnazii, adică pentru şcolile teoretice de la ei, echivalentul liceelor noastre într-o medie a nivelelor matematice (ei nu au despărţirea pe evantaiul filierelor uman până la real). Editura Ernst Klett Verlag are baze în toată Germania, dar acest manual (repet, pentru Gimnazium, adică pentru şcolile cele mai bune, pentru elevii din care se vor selecta cei ce vor merge şi la facultăţi) este pentru Land-ul Baden-Württenberg (Coordonatorul echipei de autori este August Schmid, iar manualul avizat din 1996). Capitolul despre măsurarea cercului este între paginile 74-91 (fiecare lecţie de 2 sau 3 pagini) şi are următoarele titluri: 1. Numărul cercului π; 2. Calculul ariei cercului (conţinutul cercului – Kreisinhalt); 3. Calculul lungimii cercului (perimetrului cercului – Kreisumfang); 4. Părţi de cerc (cu referire la sectorul cercului cu unghiul la centru, dar şi la desfăşurarea conului şi la elemente de astronomie şi geografia globului terestru); 5. Căi de apropiere de π (atât metoda egipteană, cât şi calcul modern adaptat calculatoarelor (aici am găsit anumite greşeli – uau! Şi calculatoarele pot greşi, iar o dată cu “ele” oamenii care lasă garda jos, având încredere că “a făcut calculatorul”); 6. Probleme combinate, aspecte istorice legate de calculul prin serii, cât şi elemente de cvadratura cercului. Cel puţin ¾ din material se încadrează liniştit sub nivelul practicat de matematica gimnazială din România (asta elitistă, cu care ne mândrim atâta). Explicaţia din lecţii este de obicei clară, la un nivel accesibil majorităţii, într-o combinaţie accesibilă de intuitiv şi teoretic. Noi avem acest manual în casă de la începutul anilor 2000. Dau aici poza unei părţi de pagină din acest manual pentru a vă face o imagine despre ce vorbesc (în traducere orientativă: cu cât împărţim un disc în mai multe părţi, cu atât mai tare reasamblarea acestor părţi se apropie de forma unui dreptunghi cu lungimea ½ P şi lăţimea r; deoarece aria rămâne tot timpul π r2, înseamnă că ½ P ∙ r = π r2 şi deci P = 2 π r, fapt care se consemnează apoi ca teoremă (U pentru Umfang, adică perimetru, iar Satz reprezintă teoremă).
Mai am două ultime observaţii generale legate de materialul în care încerc să mă lansez cu atâta precauţie. În primul rând, este evident că întregul conţinut reprezintă de fapt un amestec între nevoile reale ale unui elev de clasa a 7-a şi posibilităţile medii ale elevului de clasa a 9-a (care reprezintă totodată vârsta elevilor de a 10-a din Germania; ei nu au clasa pregătitoare). Cu alte cuvinte, materialul ce urmează reprezintă o încercare cam “înghesuită” în nivelul clasei a 7-a, atâta vreme cât în România de peste 20 de ani nu se mai face geometrie clasică în licee. Materialul ar funcţiona mult mai bine în două parcurgeri clare, una în clasa a 7-a (fără aere elitste, cât mai accesibilă majorităţii) iar a doua, recapitulativă şi cu completări, în clasa a 9-a. În condiţiile actuale profesorii trebuie să decidă cât anume şi mai ales în ce formă să prezinte materialul la clasă, în funcţie de nivelul elevilor din colectivul respectiv.
În al doilea rând, este la fel de evident că profesorul cititor trebuie să-şi ia timpul necesar pentru “digerarea” acestui material, care este în general profund diferit faţă de forma actuală de predare. În cazul meu, această formă de predare reprezintă rezultatul unui proces lung de peste 20 de ani. Prin această serie eu îmi pun la dispoziţie toată experienţa acumulată în tema respectivă.
Varianta ce o voi prezenta reprezintă o formă de lecţie, cu cunoştinţele date “de-a gata”, care nu respectă principiile predării prin problematizare, dar experienţa arată că foarte puţini elevi pot descoperi prin problematizare cunoştinţele despre măsurarea cercului, iar aceştia de fapt au aflat de mult de numărul π, aşa că demersul şi stradania în acest sens nu-şi găsesc rostul. Ca atare este mult mai bine să parcurgem cu elevii cunoştinţele într-un format oarcum clasic, organizat orientativ în următoarele trei etape: 1) Lecţia introductivă cu prezentarea cunoştinţelor pe scurt; 2) Exerciţii şi probleme; 3) Diverse căi de obţinere a formulelor (pe post de demonstraţie).
Astfel, în prima oră ar trebui să parcurgem etapa 1), primele exerciţii din etapa 2) şi eventual o primă deducere aproximativă a numărului π, ca element din etapa 3). În orele următoare vom lucra la fixarea cunoştinţelor, la extinderea nivelului de exerciţii, probleme şi aplicaţii, cât şi la alte câteva variante de deducere a numărului π accesibile nivelului clasei. Am convingerea că această formă de ordonare a cunoştinţelor este folositoare tuturor elevilor, dar mai ales elevului mediu, care primeşte “din prima” cunoştinţele de învăţat cât şi felul cum se aplică acestea. Pe acest elev nu-l interesează de unde vin aceste cunoştinţe, cum au fost ele găsite şi de ce este totul aşa cum este. Poate îl va interesa mai încolo, după ce ajunge să se împrietenească cu aceste noi cunoştinţe. Poate, după o oră-două, vom reuşi să-i trezim interesul pentru felul cum au ajuns matematicienii să-l găsească pe acest ciudat 3,14.
Există şi un alt aspect: elevul asimilează numai ceea ce înţelege, nu tot ce i se prezintă. În acest sens există oarecum două tipuri de înţelegere: cea care acoperă plaja de la intuitiv la raţional, adică mai mult sau mai puţin intelectuală, specifică elevilor buni, cât şi un substituent al acesteia, anume înţelegerea prin exersarea celor de asimilat, care este singura valabilă şi în cazul elevilor care nu înţeleg matematica. Această a doua formă de înţelegere apare însă la un elev doar dacă exersarea este făcută la un nivel accesibil capacităţii intelectuale a acestuia. Cu alte cuvinte, etapa a 2-a, cea de exerciţii şi probleme, trebuie să cuprindă din start, imediat după etapa de prezentare a cunoştinţelor, un calup consistent de exerciţii şi aplicaţii accesibile tuturor elevilor. Acestea trebuie să reprezinte “un cap de pod” în noua lecţie de cucerit, accesibil tuturor elevilor din clasă. Pe baza acestuia şi includerii sale în “zona de confort” matematic a fiecărui elev, toţi elevii vor putea în continuare să spere la înţelegerea elementelor de dificultate sporită ce vor veni. Chiar, am putea spune că exerciţiile din acest prim calup de aplicaţii ar trebui să fie de fapt la nivelul celor mai slabi elevi din clasă. Aplicaţiile de dificultate sporită, pentru elevii buni, pot veni doar ulterior acestora (după ce elevii slabi s-au liniştit, înţelegând ce se întâmplă), sau poate, chiar mai bine, doar ora următoare.
Aici avem şi o problemă de percepţie a profesorilor legată de “hrana spirituală” pentru elevii buni şi foarte buni (categoria cunoscută sub titlul de “excelenţă”). Pentru aceşti elevi trebuie să dăm aplicaţii cât mai dificile şi complicate, dar tot ei vor fi şi principalii beneficiari ai confruntării cu diferitele căi de obţinere a aproximărilor numărului π, adică a demonstrării formulelor de lungime şi arie a cercului. Ar fi absurd să considerăm că aceştia pot fi beneficiarii unei matematici provocatoare doar prin supunerea constantă la un tir de probleme dificile. Partea practică a matematicii şi de problematizarea în cazul cercetării demonstrative le poate fi la fel de folositoare, lărgindu-le puternic tabloul despre această disciplină.
Aşadar, să “purcedem la drum”.
*
1) – Lungimea şi aria cercului (lecţia introductivă) Această lecţie are rolul de a le prezenta elevilor pe scurt materialul ce urmează a fi studiat, făcându-le direct cunoştinţă cu elementele de bază ale lecţiei. De fapt aceasta reprezintă orientativ lecţia pe care o cam fac toţi profesorii. “Lecţia” ar trebui să fie scurtă, dar recomand să nu ne grăbim, poate să fie lejer undeva către 10-15 minute, la care mai adăugăm apoi şi partea de exemple.
În primul rând trebuie să le dăm aici o figură cu un cerc în care să evidenţiem cât mai clar centrul, raza şi diametrul cercului (cu notaţia acestora), iar alăturat cele două formule şi valoarea aproximativă general cunoscută a lui π, după principiul: “matematicienii au stabilit că: …”. Vom da formulele mai întâi în format aritmetic aproximativ, de felul Pcerc ≈ d ∙ 3,14 = 2 r ∙ 3,14 şi Acerc ≈ r2∙3,14. Apoi, vom explica notaţia lui π (litera grecească pentru P, de la periferie, perimetru) şi vom scrie π ≈ 3,14, explicând totodată scurt, fără multe detalii, că acest număr este un număr iraţional pentru care oamenii folosesc uzual această aproximare. Tot în acest pacheţel de formule vom da în final şi formulele exacte: Pcerc = 2 π r şi Acerc = π r2. Eu obişnuiesc să înrămez individual aceste cinci formule pentru a accentua importanţa lor. Mesajul este clar: acestea trebuie ştiute pe de rost!
Întrerup aici parcursul acestei lecţii iniţiale cu precizarea următoare: în perioada interbelică, atunci când erau oarecum obligatorii patru clase (bunica din partea mamei avea 4 clase, bunicul însă nu), la sfârşitul clasei a 4-a elevii primeau informaţii despre măsurarea cercului (lungimea şi aria) în format aritmetic aproximativ, doar cu valoarea 3,14 (fără notaţia cu π). Această lecţie avea atunci câteva aplicaţii scurte legate de butoaie şi roţi de căruţă. Acest pas nu se mai face la ora actuală şi înţelegerea sa practică le lipseşte multor elevi (cei din categoria mai “ne-matematicieni”), aşa că recomand includerea sa aici. Desigur că această parte aritmetică aproximativă s-ar putea introduce şi în finalul clasei a 5-a, undeva printre unităţile de măsură şi elementele de măsurare a pătratului şi a cercului.
2) – Exemple de calcul În finalul acestei lecţii iniţiale introductive vom face câteva exemple de calcul pentru lungimea şi aria unor cercuri, în vederea lămuririi tuturor elevilor despre scopul acestor formule. Revin cu atenţionarea că mulţi elevi le vor primi foarte speriaţi, iar noi trebuie să avem grijă să nu le perceapă ca “picate din cer”, aproape ce ceva extraterestru (aşa cum se întâmplă de obicei, iar copiii “fug acasă” la primul adult să ceară lămuriri, să ceară ajutor, despre ce s-a întâmplat). Cu alte cuvinte: ne asumăm că lecţia tot îi sperie – oricât de scurtă şi oricât de clară (de aia o şi facem cât mai scurtă, ca să nu lungim agonia sperieturii), iar imediat în continuare facem câteva exerciţii uşoare prin care să-i destresăm, prin care elevii să vadă că nu-i aşa de greu, să vadă că este de fapt un model de rezolvare în paşi puţini şi accesibili, care se repetă la fiecare exerciţiu, deci că-i uşor! Asta ar trebui să facem noi în clasă, nu să-i lăsăm să meargă acasă speriaţi şi să-i lămurească acolo cineva (dacă au cine să-i lămurească acasă; cei care n-au pe nimeni să-i lămurească sunt condamnaţi la neînţelegerea matematicii, la frica de matematică şi la analfabetism matematic).
În contextul unei predări liniştite şi ca să mă asigur că au înţeles toţi elevii, eu aş da aici sigur trei exemple cu raza şi două exemple cu diametrul dat, toate cele cinci cazuri cu dimensiunea iniţială număr întreg (de pildă: r = 5 cm; r = 8 cm; d = 12 cm; r = 11 m; d = 20 m). La toate voi cere calculul lungimii şi a ariei, în paralel prin cele două tipuri de formule, atât cu rezultate exacte teoretic (de tipul L = 16 π cm şi A = 64 π cm2), cât şi cu rezultate aproximative, dar mult mai clare pentru înţelegerea dimensiunii respective (L ≈ 50,24 cm şi A ≈ 200,96 cm2 ≈ 201 cm2). Insist aici asupra acestui fapt, amintind principiul psihologic: atunci când introduci ceva nou, cu şanse mari de sperietură prin dificultatea sa inerentă de item nou, nemaiîntâlnit şi care nici nu seamănă cu nimic din ce cunoaşte elevul, atunci vom evita să introducem din prima în datele problemei şi alte elemente suplimentare de dificultate, neesenţiale pentru înţelegerea noului subiect (nu facem “sport matematic” din prima lecţie; avem timp pentru aşa ceva mai târziu).
Fişa de lucru ar putea apoi conţine şi câteva exemple cu date fracţionare, dar aş recomanda evitarea strictă pentru prima oră a unor exemple de date iraţionale; acestea pot fi introduse în orele următoare dacă neapărat dorim. Acelaşi lucru este valabil şi pentru exemple de tipul: se dă aria şi se cere lungimea, sau invers (ştiu că pe mulţi colegi “îi arde tare” să dea din prima şi tot felul de giumbuşlucuri, dar trebuie înţeles aspectul psihologic răvăşitor la adresa unor elevi; şi să nu-mi spună cineva că el are doar elevi brilianţi în clasă, ştiu sigur că sunt peste tot din cei care se blochează, chiar şi în clasele din colegiile cele mai de vârf). În schimb, fişa de lucru ar trebui să conţină şi cel puţin încă pe atâtea exerciţii de acelaşi fel pentru temă. În partea a doua a acestei ore vom putea să ne ocupăm de deducerea formulei pentru lungimea cercului, respectiv de deducerea unei prime valori aproximative pentru numărul π (matematicienii s-au ocupat cu acest subiect sute de ani; noi putem să-i acordăm măcar un sfert de oră, din când în când).
3) – O primă deducere a numărului π se poate face prin perimetrul cercului. Pentru o înţelegere raţională a lumii (formarea unei înţelegeri nemistice, cât şi obişnuinţa de a înţelege cele ce ne înconjoară), elevii trebuie în continuare să priceapă (cât mai bine posibil, la nivelul fiecăruia) de unde vine această valoare aproximativă de 3,14 în măsurarea cercului (reamintesc părerea că nu predăm matematica doar pentru examene şi concursuri, ci şi pentru formarea unei gândiri raţionale logice la elevi; lipsa acestei gândiri s-a văzut masiv în reacţia oamenilor legată de toate situaţiile cu care s-au confruntat cu ocazia pandemiei Covit19).
Alegerea de a porni în căutarea numărului π de la perimetrul cercului nu este una uşoară, eu am încercat de-a lungul anilor şi varianta de pornire de la aria cercului (în manualul nemţesc mai sus amintit se găseşte mai întâi aria şi din aceasta se deduce perimetrul, după cum se vede în argumentaţia din poza respectivă). Cred totuşi că pornirea de la lungime este mai accesibilă majorităţii elevilor şi din punct de vedere logic, lungimea (1D), adică măsurarea de pildă în cm şi mm fiind directă, pe când aria (2D) se stabileşte indirect. Pe de altă parte, pornirea de la arie este în schimb mult mai “vizibilă” pentru elevii care şi-au format în mod sănătos şi solid simţul pentru arie, adică pentru “conţinutul suprafeţei”, aşa cum zice neamţul (Flächeninhalt). Aria cercului se vede mai bine decât lungimea acestuia, elevii fiind obişnuiţi să vadă lungimi drepte şi nu lungimi “roată”, adică circulare. Ce-i drept că ei cunosc perimetrul, iar din acest motiv ar fi mult mai sănătos dacă am vorbi despre perimetrul cercului, nu despre lungimea cercului. Pentru asta noi ar trebui însă să facem “pace cu trecutul” şi să acceptăm folosirea cuvântului cerc şi împreună cu interiorul său, adică în loc de disc (sau bulină), la fel ca la toate figurile geometrice poligonale. Astfel, în acest material eu voi vorbi în general despre perimetrul şi aria cercului, dar pentru o înţelegere generală liberă, îm rezerv dreptul de a folosi din când în când (în mod aleatoriu) şi expresiile lungimea cercului respectiv aria discului (aşa fac şi la clasă pentru că elevii mei trebuie să înţeleagă şi limbajul folosit de ceilalţi profesori). Din nou atenţionez, luaţi-vă timp să digeraţi această scurtă “filozofie” de genul “teoria chibritului” (tot ce scriu aici este rezultatul încercărilor şi al gândurilor de mulţi ani).
Începutul acestei lecţii ar trebui să fie făcut be baza unei simple observaţii la una dintre cele mai cunoscute figuri geometrice: hexagonul regulat înscris în cerc (dedus din împărţirea cercului cu compasul în şase părţi egale, desen echivalent ca proprieţăţi cu foarte cunoscuta figură mistică “floarea vieţii”), hexagon compus din şase triunghiuri echilaterale. Pe baza cunoaşterii anterioare a acestei figuri se poate observa că perimetrul hexagonului regulat este egal cu 6r, fiind deci triplul diametrului: Phexagon = 3∙d. Putem aici să folosim pe desen trei culori diferite cu care să trasăm tot câte două laturi consecutive ale hexagonului cu aceeaşi culoare, evidenţiind astfel trei diametre pe perimetrul hexagonului. Analizând figura cu hexagonul regulat înscris în cerc, putem deduce că Pcerc > Phexagon şi deci că Pcerc > 3d. Scopul acestei lecţii scurte este de a afla orientativ cu cât depăşeşte perimetrul cercului triplul diametrului.
De multe ori oamenii de rând reproşează matematicienilor că nu fac nimic practic, şi în general chiar au dreptate. În acest sens, eu propun aici o scurtă lecţie practică (o lecţie de tip “laborator de matematică”) de măsurare a perimetrului cercului şi comparare a acestuia cu diametrul. Pentru asta ne trebuie câteva recipiente rotunde şi un metru de croitorie. Elevii trebuie să măsoare diametrul recipientului şi circumferinţa acestuia, iar în final să facă o împărţire. În funcţie de acurateţea măsurărilor, rezultatul se apropie mai mult sau mai puţin de 3,14. Pentru rezultate cât mai bune trebuie însă să avem grijă la câteva aspecte.
În primul rând, recomand metrul de croitorie şi nu o ruletă, pentru că ruleta flambează şi ca urmare denaturează măsurarea, deci şi rezultatul final. Metrul de croitorie este singurul instrument menit să măsoare şi “roată împrejur”; ruleta nu se potriveşte bine la aşa ceva, exact datorită faptului că tehnic a fost gândită să se susţină singură dreaptă pe anumite lungimi.
În al doilea rând, trebuie avut mare grijă ce recipiente rotunde alegem. Din start trebuie avertizat că oalele nu sunt bune pentru că au o teşitură rotunjută pe circumferinţa bazei, aşa că nu permit o măsurare exactă a diametrului. Altele nu au această teşitură, dar nici nu sunt cilindrice ci mai mult tronconice în apropierea bazei, încurcând astfel măsurarea circumferinţei. Nouă ne-ar trebui obiecte cilindrice cu muchia bazei cât mai clară. Diverse ţevi de PVC s-ar potrivi foarte bine pentru aşa ceva (trebuie unele cu tăietură, pentru că din fabrică vin cu teşitură, iar aceasta denaturează măsurătoarea; capacul de PVC din poză are teşitură, dar are trecut şi diametrul pe etichetă, fiind făcut standard de 12,5 cm, deci teoretic nu mai trebuie măsurat diametrul, pentru că este dat. Pentru măsurarea ambelor dimensiuni, eu am folosit în ultima vreme câteva recipiente din plastic pentru diferite produse lactate (muchie destul de clară şi suprafaţă laterală aproape cilindrică, în plus legate direct de realitatea înconjurătoare a elevilor, spre deosebire de ţevile PVC care dau o tentă tehnică întregului proces, bună şi aceasta de fapt). Şi rolele de bandă adezivă sunt foarte potrivite scopului propus aici.
Conservele de tablă dimpotrivă, nu sunt prea bune pentru că au acea buză de asamblare, care introduce automat eroare. Eventual o doză mare din tablă, cum ar fi cele ce apar ocazional cu panetone, ar da o eroare mai mică din cauza faptului că influenţa buzei scade cu cât avem un diametru mai mare. În general trebuie deci să alegem obiecte care să permită o măsurare cât mai exactă a diametrului şi a circumferinţei pe acel diametru. În lipsa unui metru de croitorie, sigur că putem căuta şi alte metode de a măsura circumferinţa, de pildă prin rostogolirea unei conserve pe o coală de hârtie (astfel am putea măsura diametrul şi circumferinţa buzei conservei; vă las pe dvs. să lămuriţi metoda), sau prin înfăşurarea unei aţe ne-elastice şi măsurarea acesteia cu liniarul.
Cel mai potrivit ar fi să organizăm această scurtă lecţie pe grupe de lucru, fiecare grupă primind un obiect rotund de măsurat (desigur, de diametre diferite) şi un metru de croitorie (eventual un metru la două grupe). Se explică sarcina şi fiecare îşi face treaba. Între timp profesorul construieşte pe tablă un tabel cu patru coloane (grupa, diametrul, circumferinţa şi rezultatul împărţirii) şi linii pentru toate grupele. Reprezentanţii fiecărei grupe vin apoi şi îşi trec rezultatele în tabel. În final se analizează rezultatele şi toată lumea îşi trece tot tabelul în caiet. Eu mă gândesc că ar fi suficiente 4-6 grupe de lucru cu diametre clar diferite, dacă vrem ca tabelul să nu crească prea tare şi să fie nevoie de prea mult timp pentru copierea sa (plus că pot apărea erori de copiere în caiet la tabele cu prea multe linii). Este evident că ne vom bucura de orice rezultat între 3,1 şi 3,2,
Aceasta ar fi o metodă practică de obţinere a unei aproximări onorabile pentru numărul cercului, adică pentru 3,14 drept “raportul dintre circumferinţa şi diametrul cercului” (observaţi că am folosit denumirea de raport pentru π, la fel cum folosesc acest cuvânt şi la “rapoartele trigonometrice” în gimnaziu, în loc de “funcţii trigonometrice” specifice trigonometriei din liceu) Ca o scurtă observaţie, în contextul ideii de raport, consider că sunt absurde exerciţiile în care elevii primesc o lungime egală cu π cm. Desigur că această lungime există, de pildă la cercul cu diametrul sau cu raza unitate, dar în clasele gimnaziale nu ar trebui să practicăm astfel de giumbuşlucuri de “matematică sportivă” potrivite mai degrabă maturităţii matematice din liceu, eventual materiei din jurul şi de după studiul cercului trigonometric.
Închei această primă parte a lecţiilor cu o scurtă întâmplare anecdotică. În urmă cu mulţi ani, am predat la cerc doar lecţia de bază, cu explicaţiile de rigoare că 3,14 este o valoare aproximativă şi că numărul π are o infinitate de zecimale, care apar neperiodic, etc. În ora următoare un elev a ridicat mâna şi mi-a zis că verişorul lui, care este în liceu, i-a spus că numărul π este exact 3,14! Da, da! Nu are rost să mă pun eu cu verişorii ăştia mari, că ştiu ei mai bine. CTG
P.S. Având ceva mai mult timp cu ocazia acestei “vacanţe forţate” de PDV (pandemia de Corona virus), m-am uitat în câteva cutii cu cărţi la care n-am umblat de mult şi surpriză! Să vezi şi să nu crezi ce-am găsit: un manual de clasa a 7-a din Austria din 1977 (Rinderer Leo, Laub, Josef, şa, Mathematik 3.Kl. Ed. Hölder-Pichler-Tempsky, Viena, cam pentru vârsta elevilor din clasele noastre de a 6-a). Răsfoiesc eu prin manual în căutarea unor lecţii interesante şi aşa ajung şi la lecţiile despre măsurarea cercului. Aici prima lecţie este despre lungimea cercului şi, în principiu spune cam ce am zis şi eu mai sus, anume îi pune pe elevi să măsoare circumferinţa şi diametrul unui obiect cilindric. Interesant este felul în care sunt îndrumaţi elevii să măsoare circumferinţa cercului, anume să înfăşoare o aţă ne-elastică (precizat clar) de 10 ori în jurul cilindrului, să măsoare exact acea aţă şi să ia pentru circumferinţă a zecea parte din rezultat (?). Oare astfel se evită mai bine greşeli de măsurare? Se prea poate (pag. 209).
Câteva pagini mai încolo, la lecţia despre aria cercului, apare din nou descompunerea discului recompusă în formă de dreptunghi, prezentată la începutul acestui eseu, într-o variantă puţin diferită, folosită de data asta pentru trecerea de la perimetrul cercului către aria sa. Interesante sunt aici apariţia a două noi formule pentru arie în funcţie de diametru: formula exactă A = d2 π / 4 şi formula aproximativă A = 0,785 ∙ d2.
Conţinutul acestei imagini poate fi folosit uşor ca bază pentru o primă încercare în deducerea ariei cercului. Fie la finalul primei ore descrisă mai sus, fie ca temă inclusă în finalul fişei de lucru din prima oră, fie în următoarea oră se poate face următoarea lucrare practică: elevii vor trebui să construiască pe hârtie colorată şi să le decupeze cele două figuri echivalente în paralel, discul împărţit în 8 părţi egale şi alăturat reasamblarea pieselor în formă “dreptunghiulară” (cei curajoşi primesc desigur recomandarea să facă împărţirea în 16 părţi egale). Vedeţi că această ultimă imagine are un mic pas în plus faţă de reasamblarea din prima imagine, anume că aici o optime a fost tăiată în jumătăţi, fiecare din acestea fiind lipită la câte un capăt al şirului celorlalte şapte optimi, astfel încât figura compusă seamănă şi mai bine cu un dreptunghi decât cu un paralelogram (având lăţimea perpendiculară pe “lungime”).
Vedeţi în imagine că oricum această lucrare practică este recomandată prin forfecuţa reprezentată la început lângă nr. 1155 (în colţul din stânga sus). Autorii recomandă în text o rază de 6 cm, dar mult mai interesant, ne recomandă să decupăm discurile şi să obţinem împărţirea în opt părţi egale prin împăturiri succesive a acestora: prima împăturire în jumătăţi, a doua în sferturi, iar a treia în optimi. Unul dintre aceste sectoare de cerc trebuie împărţit încă în două de-a lungul axei sale de simetrie; aceste două bucăţi sunt cele care se vor pune la capete.
Dacă alegem această cale şi dorim să mergem până la şaisprăzecimi, atunci va trebui să ne pregătim cu hârtie cât mai subţire, pentru că hârtia normală de copiator nu se lasă împăturită cu exactitate de prea multe ori. Puteţi lucra totuşi şi pe hârtie de copiator, dar după fiecare pliere faceţi direct tăierea sau ruperea celor două jumătăţi. Aici desigur că le vom povesti că această transformare este doar o imagine intuitivă, practică, orientativă pentru fenomenul studiat; este evident că forma obţinută nu este un dreptunghi pentru că are lungimile ondulate, dar acestea vor deveni tot mai drepte cu cât vom descompune discul în tot mai multe sectoare de disc.



Sunt impresionat.
Sunteti primul profesor pe care l-am intlanit si de la care aflu ca isi pune problema “oare cat asimileaza elevul din ce i se prezinta”.
Ma pregatesc sa dau bacul (in eventualitatea in care se va da vara asta) la mai multi ani dupa un liceu facut la fara frecventa.
Cu tristete descopar ca nu s-au schimbat foarte multe in modul de predare de acum 22 de ani, cand am terminat eu clasa a 8 a. Din ce tin minte, regulile jocului erau asa: eu predau, e treaba ta sa intelegi. Datoria mea e sa iti livrez informatia.
Ce mi se pare greu de inteles de fapt, este motivul pentru care profesorii se multumesc cu rezultate atat de slabe.
Sa ma explic: in mod cert, din punctul meu de vedere, volumul de materie este coplesitor. In primul rand pentru elev, si sunt convins ca si pentru profesor. Consider ca profesorii ar trebui sa puna presiune in sus in sistem, pentru simplificarea materiei. In ideea ca nu intentionam sa trimitem copiii la NASA imediat dupa gimnaziu sau liceu.
O materie care acopera lucrurile esentiale, le cuprinde pe cele practice, aplicate (cred ca ex manualului german e foarte bun, traiesc in Norvegia de cativa ani, iar scoala de aici difera enorm de cea din Romania), si le da la o parte pe cele care merg in profunzime, cred ca ar fi mult mai eficienta.
E un mai mare castig sa aduci toti elevii la un minim nivel de 7 si sa ai cateva varfuri de 10, decat sa te concentrezi pe cei de 10 care “vor sa invete” , neglijandu-i pe cei care nu inteleg, si in consecinta nu ii intereseaza.
Insa pentru a aduce nivelul mediu mai sus, e nevoie ca probabil 30% din materie sa dispara. Este de asteptat ca profesorul nu are timpul fizic pe care sa-l dedice celor care nu pot tine pasul, pentru a-i ajuta sa asimileze tot. Si atunci singura solutie e sa nu ne mai amagim ca avem o materie avansata pe care o predam, pentru ca o predam degeaba unei bune parti a elevilor.
Dar presupun ca multi profesori, la fel ca societatea romanesca in general, traieste cu ideea: “chiar daca vreau sa schimb ceva, ma bat cu morile de vant”. Corect, insa nu sunt alternative.
Inca o data, respect pentru ce faceti, am citit un pic pe-aici si va apreciez stilul si abordarea. De asa ceva chiar e nevoie.
Multa bafta in ce faceti, s-o tineti asa !