Săptămânile trecute am avut în vizită o elevă de clasa a VI-a de la Roma, care a adus şi caietul de geometrie cu ea. Tare ne-am mai distrat cu acest caiet, care conţinea un amestec ciudat de geometrie “cu aer de” texte din melodiile lui Toto Cutugno şi Eros Ramazotti. Să vă prezentăm câteva exemple care ne-au plăcut mai mult.
Angoli speciali …Se ruotondo la semiretta compie un giro completo, sovrapponendosi a se stressa, forma un angolo giro. Dacă n-aţi înţeles, este o parte din lecţia despre unghiuri speciale, anume definiţia unui unghi în jurul unui punct (unghiul plin sau complet, cel de 360o).
Iată şi un pasaj unde se vorbeşte despre numărul de diagonale ale unui poligon: In un quadrilatero possiamo disegnare solo due diagonali, in un pentagono cinque, in un esagono sono nove. Il triangolo è l’unico poligono privo de diagonali. Clar, nu?
Trecând la lucruri mai serioase, am găsit şi o minunată demonstraţie pentru suma unghiurilor unui poligon (imaginile sunt refăcute după lecţia din caietul respectiv) folosită, culmea, pentru demonstrarea sumei unghiurilor în triunghi, ca un caz particular. Iată în continuare această demonstraţie:
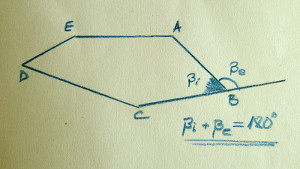
Gli angoli del poligono sono sio interni che esterni, quesi ultimi sono determinati da una lato del poligono e dol prelungiamento del lato consecutivo:
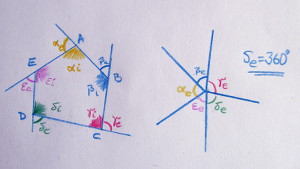
Să explicăm raţionamentul: din prima imagine deducem că suma tuturor unghiurilor din figură este S = Si + Se = 5 ∙ 180o
Combinând cu informaţia din a doua imagine, deducem că: Si = 5 ∙ 180o – 2 ∙ 180o, adică Si = (5 – 2) ∙ 180o
Deci, cum am spune noi, Si = (n – 2) ∙ 180o
Prof. Mariana şi Titus Grigorovici
Ciao Roma! 4.04.2016