Programa actuală pentru clasa a VIII-a prevede un început intuitiv pentru geometria în spaţiu, prin prezentarea câtorva corpuri la început, pentru a putea fi folosite în problemele din lecţiile următoare. Aceasta este însă doar o jumătate de pas înspre accesibilizarea materiei, pentru că lecţiile merg în continuare tot în forma riguros – demonstrativă, accesibilă intelectual doar unui număr extrem de restrâns de elevi. Toţi ceilalţi, marea masă a elevilor de a VIII-a, urmează a se chinui încă mult, până când în sfârşit vor apărea formulele de arie şi volum şi vor putea face şi ei liniştiţi o problemă de geometrie, fără să tremure că iar nu ştiu.
Ne-am propus, pentru această postare, să arătăm cum am făcut anul acesta prezentarea primului corp – a cubului – într-o formă care să le ofere elevilor o alunecare cât mai lină în noua geometrie.
Pentru început am făcut un exerciţiu de vizualizare în spaţiu a unor „corpuri” formate din beţe (eu am avut acces la o grămadă de cozi de mătură). Puteţi vedea pe Youtube ceva similar în postarea colegilor de la Şcoala liberă Waldorf din Bucureşti (Studiul matematicii in gimnaziu – Scoala Libera Waldorf).
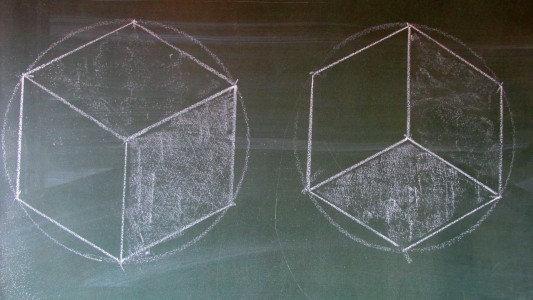
Apoi am trecut la tablă, respectiv elevii în caiete, şi am încercat diferite reprezentări 2D ale cubului, reprezentări care trebuie să păcălească ochiul şi creierul pentru a percepe vizual un cub care este un corp 3D (ca să folosesc limbajul preferat de elevi). Primele două sunt destul de surprinzătoare, pentru că sunt generate din construcţia hexagonului regulat cu rigla şi compasul (vezi prima imagine). Următoarele două figuri sunt mai obişnuite; găsiţi pe a doua imagine detaliile de construcţie.
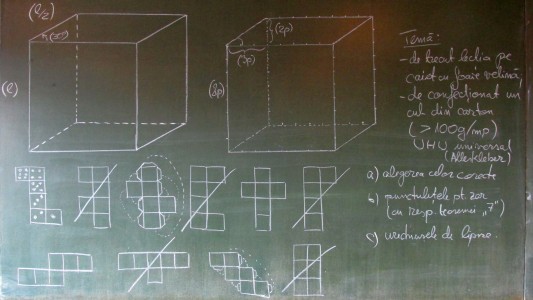
În continuare am făcut trei exerciţii deosebite, pentru dezvoltarea imaginaţiei în spaţiu, legate de desfăşurările cubului. Trebuie să precizez că eu nu sunt de acord cu cuvântul „desfăşurare”: acesta presupune cubul deja existent, pe care apoi îl desfăşurăm. Or, noi vorbim aici de procesul invers: elevul va trebui să deseneze „desfăşurarea”, pentru ca apoi să asambleze din aceasta un cub. Nici cuvântul din limba germană nu este prea strălucit, ei folosind cuvântul Netz, care înseamnă reţea, plasă (echivalentul cuvântului net din engleză). Cu această prealabilă „strâmbătură din nas”, să trecem la cele trei exerciţii, pe care le vedeţi în a doua imagine.
- Care din următoarele figuri reprezintă cu adevărat desfăşurări corecte ale unui cub?
- Presupunând că vrem să construim un zar, elevii trebuie să aşeze pe desfăşurările corecte numerele conform regulii de 7 a zarului.
- Pentru a putea asambla un cub este nevoie de urechiuşe de lipire. Elevii trebuie să ataşeze aceste urechiuşe desfăşurărilor corecte.
Toate cele trei exerciţii forţează imaginaţia elevilor în spaţiu, fiind extrem de savurate de către toţi elevii. Tema a fost, apoi, să confecţioneze un cub din carton. A doua zi, la discuţia despre cuburile din carton aduse de elevii harnici, a apărut următoarea obsevaţie: se pare că la toate variantele de desfăşurări corecte, elevul trebuie să proiecteze exact 7 urechiuşe de lipire. Este o proprietate interesantă ce poate fi uşor verificată şi chiar explicată, trezind totuşi uimirea: iarăşi numărul 7? Despre explicaţie, aceasta vine simplu: trebuie făcute 7 lipituri pentru că la fiecare desfăşurare corectă sunt exact cinci îndoituri pe muchii (7 + 5 = 12 muchii ale cubului).
În afară de discuţia de la „verificarea temei”, ora următoare am avut o activitate mult mai tradiţională: figură + prezentarea tuturor formulelor pentru arie, volum (dictate de către elevi – cei care gândesc le pot genera singuri) şi pentru diagonala cubului. La demonstrarea ultimeia se aplică teorema lui Pitagora în ΔD’DB care este dreptunghic dintr-un motiv extrem de simplu: latura [BD] este orizontală, fiind inclusă în baza cubului, pe când latura [D’D] verticală, deci cele două sunt perpendiculare una pe cealaltă (intuitiv, nu-i aşa?). În final am făcut exerciţii de calcul în toate formele şi pentru toate categoriile de elevi. Considerăm că o astfel de abordare i-ar ajuta pe cei mai mulţi elevi să aibă o legătură ceva mai prietenoasă cu ora de matematică.
3 oct. 2016
Titus & Mariana Grigorovici