Noua programă pentru Evaluarea Naţională 2020 a apărut în Monitorul Oficial în Vinerea Mare; eu am citit-o în ajunul Paştelui şi m-am şi apucat să scriu, într-o refulare de profundă indignare, despre trunchierea mult prea radicală a materiei, prin eliminarea întregii părţi de “geometrie aritmetică” de clasa a 8-a, adică a părţii accesibile majorităţii elevilor, lecţii pe care foarte mulţi elevi le parcurseseră în mare parte şi le stăpâneau. Nu că nu mă aşteptam la această mişcare, dar undeva în sufletul meu speram la o decizie mai raţională din partea autorităţilor. Apoi, în sfânta, dar profund interiorizata zi de Paşte m-am hotărât să mă liniştesc şi să aştept să văd ce se mai întâmplă. Cred că am aşteptat destul.
Deşi trunchierea programei pentru EN prin tăierea întregii materii de semestrul al II-lea este cunoscută de către toată lumea, se pare că nimeni “nu a avut ochi” pentru uriaşa nedreptate făcută marii mase a elevilor prin eliminarea din materia de examen a formulelor de calcul a ariilor şi volumelor corpurilor geometrice de bază (prisme şi piramide). Covit-ul şi toate deciziile autorităţilor ne-au ocupat aparent tot timpul. În astfel de situaţii cine mai are vreme să se uite la ce lovitură au primit nişte copii? Şi nu mulţi, vorbind aici de marea masă a elevilor de nivel mediu.
Haideţi să analizăm această situaţie, cât şi cauzele ei. Pentru că, aşa cum orice accident îşi are cauzele sale, uneori vechi şi acumulate, tot aşa situaţia actuală îşi are cauzele ei ignorate ani la rândul de autorităţile dominante în matematica şcolară românească.
Să ne lămurim clar: în urma “vacanţei” forţate de starea de urgenţă generate de pandemia de Covit 19, din materia generală pentru EN s-au scos două categorii de lecţii. În primul rând s-au scos lecţiile ce urmau a se parcurge în perioada martie-mai şi care nu fuseseră efectiv predate la clasă în cele mai multe cazuri (trunchiuri de piramide, corpuri rotunde, inecuaţii etc.).
Dar s-au mai scos şi multe lecţii care fuseseră de fapt parcurse. Aici intră pe de-o parte lecţiile care erau oricum incluse şi pentru simularea oficială a EN ce era programată prin 20 martie. De vreme ce acestea erau parcurse de majoritatea profesorilor şi învăţate deja de cei mai mulţi elevi, de ce au fost scoase? Este cazul concret al funcţiilor (de gr.I), care aduceau un exerciţiu uşor (reprezentarea grafică), accesibil tuturor elevilor, dar şi un exerciţiu mai greu, renumitul “punctul b)” care-i aducea în stare de tremurat pe mulţi elevi (asta după parcurgerea în cele mai bune condiţii a două luni de şcoală din semestrul II!). Aceleaşi lucruri pot fi susţinute despre operaţiile cu fracţii algebrice (rapoarte de numere reale reprezentate prin litere), care fuseseră parcurse conform programei chiar înaintea funcţiilor, în general pentru teza din semestrul I. De ce s-au scos acestea din programa de examen?
Dar tot aici intră şi partea de geometrie aritmetică, anume calculele de arii şi volume la prisme şi piramide. Această parte nu era tradiţional inclusă pentru simularea EN, dar din câte am văzut eu majoritatea profesorilor o parcurseseră, pur şi simplu pentru că nu-şi permiteau să lase atâta materie neparcursă până după simulare. Iar dintre acestea însă, două formule fuseseră oricum parcurse în clasa a 5-a: volumul cubului şi al paralelipipedului dreptunghic. Acestea de ce au fost scoase din materia de examen şi înlocuite cu înjositoarele “determinaţi aria patrulaterului ABCD” (un pătrat cu latura dată) sau “determinaţi perimetrul triunghiului ABC” (echilateral cu latura dată) etc., cu evidente accente de pomană electorală.
Trunchierea materiei nu i-a afectat tare mult pe elevii buni; aceştia s-au adaptat uşor la noile titpuri de probleme introduse după vacanţa de Paşte prin testele de antrenament (teste pentru care ministerul merită într-adevăr toate laudele şi mulţumirile aferente). Trunchierea materiei însă i-a afectat foarte mult pe marea masă a elevilor de mijloc (blocul central din “Clopotul lui Gauss”), cei care aveau un punct de sprijin puternic în “geometria aritmetică”, adică în partea de calcul a ariilor sau volumelor unor corpuri. Mare parte din pregătirea lor de clasa a 8-a a fost aruncată la gunoi cu o indiferenţă greu de înţeles. Pentru mulţi, pentru prea mulţi elevi de clasa a 8-a, acest pas a reprezentat un adevărat dezastru pentru că li s-a scos din programă partea cea mai accesibilă din geometrie.
Ajunseseră şi ei, după îndelungi eforturi, să stăpânească fiecare la nivelul lui calculele din teorema lui Pitagora şi cele câteva formule, şi brusc s-au trezit “cu ochi-n soare”. Ajunseseră şi ei să facă cu demnitate şi un pic de “geometrie”, când brusc această “geometrie” le-a fost eliminată, înjosiţi fiind cu un substituent banal, care sigur nu are darul de a le întări încrederea în sine, ci mai degrabă acţionează ca o confirmare oficială de tipul “tu eşte de fapt prost, haide să nu ne mai prefacem, uite, îţi dăm să calculezi aria unui dreptunghi cu laturile date şi gata, stai cuminte în banca ta şi taci”.
Dar, de ce s-a ajuns în această situaţie, ca în cazul de criză pe care-l cunoaştem cu toţii, ministerul, aplicând un principiu normal în această situaţie, să ajungă să lovească în atâţia elevi? Din câte am înţeles, situaţia la examenul paralel de Lb. Română nu a presupus astfel de dezavantaje şi inechităţi, şi nici la nivelul BAC-ului nu au fost probleme de astfel de magnitudine. Vom înţelege cauzele acestui dezastru dacă ne vom uita puţin mai atent la structura materiei de geometrie din clasa a 8-a. Pentru o cât mai clară înţelegere, permiteţi-mi să apelez la o descriere simplistă a materiei de geometrie de a 8-a, catalogând lecţiile minimal cu “uşor” sau “greu”, eventual un mix dintre acestea.
- Puncte, drepte, plane: convenţii de notare, reprezentări etc.: uşor-greu;
- Corpuri geometrice, reprezentare în desen; elemente caracteristice, desfăşurări: uşor;
- Paralelism (unghiul a două drepte, dreaptă paralelă cu plan etc.): greu;
- Perpendicularitate (dreaptă perpendiculară pe plan etc.): greu;
- Proiecţii pe un plan (unghiul dintre o dreaptă şi un plan etc.): greu;
- Teorema celor trei perpendiculare: greu;
- Distanţe şi măsuri de unghiuri în corpuri: uşor-greu;
- Arii şi volume ale unor corpuri geometrice: uşor.
Să nu ne lăsăm păcăliţi de aparenţe: lecţia de prezentare a corpurilor geometrice se parcurge de obicei în 2 ore, dar elevii mai slabi nu au ce să facă cu ea tare mult în următoarele trei luni (doar să le tot deseneze). Întreg semestrul I şi încă un pic din semestrul II sunt ocupate de acel bloc central de lecţii despre drepte şi plane cu demonstraţii (uneori şi calcule), deseori foarte abstracte, inaccesibile marii mase a populaţiei şcolare. Această parte de materie reprezintă însă zona principală pentru olimpiadele şcolare şi din cauza asta este “în faţă”, după principiul de-a dreptul răutăcios “de cei buni ne ocupăm la început; cei mulţi şi proşti să aştepte până în semestrul II”.
Partea despre arii şi volume apare doar la coadă (nici nu este inclusă pentru simularea din martie), când în sfârşit atenţia pare să se îndrepte şi asupra ne-olimpicilor. Indiferenţa faţă de marea masă a elevilor merge în unele cazuri şi mai departe, în şcolile “de centru” existând profesori care nici nu mai predau partea de arii şi volume, după principiul “şi-aşa au toţi profesori în particular”. În cazul vacanţei forţate de Corona-virus şi a programei de avarie din aprilie, oare care parte a rămas “pe de lângă”? Cum se zice: ghici-ciupercă ce-i? E clar că cei mulţi dar slabi la demonstraţii geometrice au rămas văduviţi de singurele situaţii unde puteau dovedi cu demnitate că ştiu şi ei să facă “olecuţă de geometrie”.
Pentru o minte de matematician deschisă şi cu respect şi faţă de ceilalţi, faţă de cei ne-matematicieni, lucrurile au o soluţie foarte clară, dar pe care gestionarii matematicii româneşti pur şi simplu refuză să o vadă (sau poate sunt doar incapabili să o vadă, probabil datorită fantomelor din trecut ce le bântuie încă gândirea). Soluţia de care vorbesc ar consta în mutarea ariilor şi volumelor la începutul semestrului I, în aceeaşi lecţie cu prezentarea corpurilor, desigur într-o formă mai extinsă. Mutarea respectivă, a cel puţin unei părţi a corpurilor, ar oferi din start material de procupare şi celor 80-90% din elevi care cu greu fac faţă părţii la demonstraţii despre drepte şi plane. În acest fel, se pot parcurge lejer la început prismele şi piramidele, lăsând pentru finalul semestrului II trunchiurile şi corpurile rotunde. O astfel de aranjare ar aduce o situaţe de respect echilibrat între cele două categorii de elevi: cei puţini dar buni şi cu care facem performanţă, dar şi cei mulţi şi mediocri la matematică, dar care sunt şi ei cetăţeni ai acestei ţări şi pe care avem totuşi datoria să-i educăm la un nivel acceptabil.
Dar cum s-ar putea parcurge corpurile fără o serioasă pregătire prealabilă din punct de vedere a dreptelor şi planelor? (aţi putea întreba, stimaţi cititori) Păi simplu: în mod intuitiv!!! Cuvântul respectiv este oricum readus la viaţă şi ridicat la mare preţ în noua programă. Dar n-au nevoie de teorema celor trei perpendiculare, de pildă, la găsirea apotemei pentru aria laterală? (ar putea întreba cineva) Nu! Pentru că acum avem doar corpuri regulate, iar apotema piramidei este de fapt înălţimea într-un triunghi isoscel, deci nimereşte evident în mijlocul muchiei bazei. Dar cu înălţimea care-i perpendiculară pe planul bazei, cum facem? Să caute răspunsurile cei abilitaţi şi plătiţi pentru asta, că eu le-am căutat şi le-am găsit în urmă cu 20 de ani şi de atunci predau aşa cum am descris, iar materia curge extrem de lin, vă pot asigura. La sfârşitul lui octombrie avem parcurse prismele şi piramidele, cu toate ariile şi volumele, diagonale şi tot felul de secţiuni, după care majoritatea elevilor au de lucru. Doar apoi încep studiul complet al dreptelor şi al planelor, studiu pe care îl termin până la vacanţa de iarnă (în clasele unde mergem mai greu, rămânând câte o lecţie două pentru ianuarie).
Pe finalul redactării acestui text am văzut şi eu subiectele date la EN şi da, văd că am uitat să amintesc la banalităţile actuale şi perimetrul unui paralelogram cu laturile date. Analizând subiectele date la examen vedem că, din geometria în spaţiu au rămas doar cubul şi paralelipipedul dreptunghic din lecţia uşoară cu reprezentarea corpurilor, care fuseseră oricum predate din clasa a 5-a, (a cam dispărut şi piramida), dar au rămas în schimb unghiul dintre două drepte (în forma sa stupidă de perpendicularitate) şi planele paralele, inclusiv distanţa dintre acestea (dreaptă perpendiculară pe plan) într-o semi-piramidă. Pentru ce am mai învăţat toate acele corpuri cu elevii???
Este clar că această situaţie ne-a prins total pe nepregătite ca sistem, din punct de vedere a geometriei în spaţiu, relativ la cei 80% din elevii de clasa a 8-a care nu pot face demonstraţii din această parte şi desigur că nici nu s-au uitat la cerinţele respective.
În căutarea unei soluţii de rezolvare a acestei situaţii, tardiv faţă de cei care au terminat clasa a 8-a, dar măcar preventiv faţă de cei ce vin de la anul în a 8-a (şi pentru care autorităţile nu ne prea prevăd un an şcolar în condiţii obişnuite), poate că onorabili decidenţi ar trebui să se uite şi prin manualele din străinătate, nu de alta dar acolo nu se face partea de studiu a poziţiilor relative drepte-plane, şi poate găsesc la aceia o idee pentru cale de a ieşi din impas.
Cât despre România, ordinea din programa actuală este foarte veche, dar partea de drepte şi plane era pe vremuri studiată mult mai intuitiv şi mai scurt. Am “dat o căutare” prin raftul cu manuale vechi şi am constatat că de la cel mai vechi manual postbelic găsit în casă (un “Hollinger” din 1957) organizarea este cam aceeaşi, cu precizarea că până în 1980 manualele lui Hollinger aveau partea de studiu a dreptelor şi planelor extrem de accesibilă şi restrânsă, predată deosebit de intuitiv.
Titlul iniţial al acestui articol a fost Dezastre în matematica şcolară, dar l-am considerat în final prea dur şi exagerat. Nu cred să fi murit vreun elev din cauza acestei situaţii, dar sunt convins că i-a afectat pe mulţi în sens negativ (diferiţi elevi sau părinţi mi-au confirmat acest punct de vedere). Sunt convins totodată şi că, alături de multe altele, această excludere îşi aduce aportul corespunzător la îndepărtarea de matematică a elevilor de inteligenţă medie.
Între timp am ajuns şi la “afişarea notelor” (anul acesta cu ghilimelele de rigoare), iar rezultatele susţin oarecum cele spuse aici, în sensul că foarte mulţi elevi slabi şi medii au reuşit totuşi note destul de bune, peste aşteptările mele ca profesor care le cunosc nivelul activităţii. Statisticile susţin aceste spuse, confirmând că s-a dat mult prea uşor, chiar şi pentru cei slabi, trecându-se mult dincolo de pragul necesar situaţiei concrete, urmare a faptului că nu s-a prea lucrat cu clasele după 10 martie
De unde au apărut aceste note “cam prea bune”? Păi, de la acei itemi din EN mult prea banali (pe post de mită electorală), puşi acolo ca să închidă gura posibilelor frustrări naturale ale elvilor şi a familiilor acestora prin scoaterea elementelor de geometrie aritmetică, elemente accesibile acestora, dar pentru rezolvarea cărora elevii de nivel mediu ar fi trebuit să se concentreze bine. Aşa, toţi aceştia nu a mai fost nevoie să se mobilizeze prea tare, iar toată lumea e mulţumită (aparent). Dar cu ce preţ pentru viitor? De acest aspect nu am auzit să discute cineva.
Cum ar arăta rezultatele unui studiu PISA pe această generaţie de elevi? (oare, chiar pe ei se va aplica studiul la anu’ în 2021?) Dar, nu!, staţi!, vor spune unii, acum există circumstanţe atenuante, fiind o situaţie total atipică. Spuneţi-le asta părinţilor acestor absolvenţi. De ce doar copiilor de nivel matematic mediu le-a fost eliminată geometria accesibilă dar mobilizatoare, pe când elevilor buni le-a rămas pentru examen aproape întreagă materia de geometrie de a 8-a?
Cum îi vom mai mobiliza noi la anu’ pe elevi să înveţe ariile şi volumele corpurilor, când există clar posibilitatea repetării şcenariului? Oare, la anu’ vom avea încă o generaţie care nu va fi nevoie să înveţe arii şi volume? Că s-a întâmplat acum mai este cumva de înţeles: aşa a fost momentul şi trebuia luată o decizie. Că se va întâmpla din nou în cazul viitoarei generaţii, asta nu va mai fi de iertat!
De fapt, de unde există această indiferenţă a decidenţilor matematici faţă de geometria pentru elevii de rând? De unde această lipsă de respect faţă de datoria de formare a gândirii practice matematice şi la oamenii de rând? De ce decidenţii matematicii şcolare româneşti se ocupă în primul rând doar de ce buni, şi numai apoi de cei mulţi şi slabi iar aceasta în mod absolut colateral şi superficial?
Cititorului care are impulsul să minimalizeze cele susţinute în prezentul articol îi transmit doar că se face prin acest gând co-făptaş moral la situaţia constatată prin iarnă de raportul la studiul PISA 2018, legat de marele procentaj de analfabeţi funcţional scos în evidenţă în şcolile româneşti la elevii de 15-16 ani. CTG
P.S. Pentru cei care se gândesc să susţină că acest caz este unul izolat, vreau să amintesc un altul despre care puţini îşi mai aduc aminte. Poziţionarea până anul trecut a lungimii şi ariei cercului în finalul clasei a 7-a, de obicei după teză, le condamna şi pe acestea deseori la neînvăţare. În cazul tezelor unice din urmă cu 12-13 ani acestea au rămas doi ani pe din afara materiei pentru teză şi nimeni nu le mai parcurgea ulterior (aceeaşi soartă au avut-o atunci şi corpurile rotunde în finalul clasei a 8-a). Poate că pe vremea aceea se ocupa cu meditaţiile la matematică şi Tanti Viorica, de l-a uitat în starea de stress pe dragul de π (cine ştie?).
Eu sunt însă convins că la toamnă nici un profesor de liceu nu va avea grija “recuperării” lecţiilor neparcurse din geometria de a 8-a (aşa cum susţinea sus şi tare D-na Ministru). Mă gândesc de pildă la corpurile rotunde, care din nou rămân “de căruţă”. Iar apoi, peste ani şi ani, poate se trezeşte careva din această generaţie de absolvenţi că vrea să ajungă preşedinte, iar o jurnalistă ciudată îl va întreba cât este aria sferei … (Salutări de la Unchiu’ Marinică, cel cu “unde este π?”; recitiţi povestea adevărată pe http://pentagonia.ro/%cf%80-da-unde-este-%cf%80/ ) Apropos, π de ce a fost eliminat subtil din acest examen? Că elevii aceştia chiar îl cunoşteau bine, după spectacolul mediatic din toamnă cu ocazia alegerilor prezidenţiale. Te pomeni că s-a decis să fie ţinut o vreme “pe tuşă” pentru că prea a ajuns implicat politic???

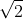 şi BC=2
şi BC=2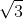 . Pe planul dreptunghiului se ridică, în punctul D o perpendiculară pe care se ia un punct P. Se consideră de asemenea M şi N picioarele perpendicularelor din A respectiv C pe dreapta PB, despre care se ştie că MN = 1. Să se calculeze lungimea segmentului (PB).
. Pe planul dreptunghiului se ridică, în punctul D o perpendiculară pe care se ia un punct P. Se consideră de asemenea M şi N picioarele perpendicularelor din A respectiv C pe dreapta PB, despre care se ştie că MN = 1. Să se calculeze lungimea segmentului (PB).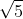 . Notăm cu A, B respectiv C ariile celor trei triunghiuri dreptunghice MNP, MPR şi NPR, iar cu D aria triunghiului MNR. Demonstraţi că A2 + B2 + C2 = D2.
. Notăm cu A, B respectiv C ariile celor trei triunghiuri dreptunghice MNP, MPR şi NPR, iar cu D aria triunghiului MNR. Demonstraţi că A2 + B2 + C2 = D2.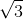 => x = ± 3. Cum arată o astfel de rezolvare în lecţia televizată (lecţie despre care autorităţile susţin că este accesibilă tuturor elevilor din ţară, inclusiv celor care nu au acces la internet)? Păi, simplu, uite aşa: (2x + 1)2 – 9 = 0 <=> (2x + 1)2 = 9 => | 2x + 1 | =
=> x = ± 3. Cum arată o astfel de rezolvare în lecţia televizată (lecţie despre care autorităţile susţin că este accesibilă tuturor elevilor din ţară, inclusiv celor care nu au acces la internet)? Păi, simplu, uite aşa: (2x + 1)2 – 9 = 0 <=> (2x + 1)2 = 9 => | 2x + 1 | = 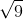 => 2x + 1 = ± 3 etc. Clar, nu? Întrebaţi pe un copil din vecini, dar nu pe unul dintre aceia foarte buni, şi vedeţi ce vă spune. Tare aş vrea să aud justificarea unui “pedant” explicând la ce naiba ajută modulul acela în această situaţie
=> 2x + 1 = ± 3 etc. Clar, nu? Întrebaţi pe un copil din vecini, dar nu pe unul dintre aceia foarte buni, şi vedeţi ce vă spune. Tare aş vrea să aud justificarea unui “pedant” explicând la ce naiba ajută modulul acela în această situaţie